2.5 二次函数与一元二次方程(2)一课一测
文档属性
| 名称 | 2.5 二次函数与一元二次方程(2)一课一测 |

|
|
| 格式 | doc | ||
| 文件大小 | 672.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-24 00:00:00 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
2.5 二次函数与一元二次方程
第二课时检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
1.(2017秋 新罗区校级期中)已知一 ( http: / / www.21cnjy.com )元二次方程1﹣(x﹣3)(x+2)=0,有两个实数根x1和x2,(x1<x2),则下列判断正确的是( )www.21-cn-jy.com
A.﹣2<x1<x2<3 B.x1<﹣2<3<x2
C.﹣2<x1<3<x2 D.x1<﹣2<x2<3
2.(2017 兰州)下表是一组二次函数y=x2+3x﹣5的自变量x与函数值y的对应值:
x 1 1.1 1.2 1.3 1.4
y ﹣1 ﹣0.49 0.04 0.59 1.16
那么方程x2+3x﹣5=0的一个近似根是( )
A.1 B.1.1 C.1.2 D.1.3
3.(2017 徐州模拟)二次函数y=﹣x ( http: / / www.21cnjy.com )2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
( http: / / www.21cnjy.com )
A.t>﹣5 B.﹣5<t<3 C.3<t≤4 D.﹣5<t≤4
4.(2017 山西模拟)小李同学在求一元 ( http: / / www.21cnjy.com )二次方程﹣2x2+4x+1=0的近似根时,先在直角坐标系中使用软件绘制了二次函数y=﹣2x2+4x+1的图象(如图),接着观察图象与x轴的交点A和B的位置,然后得出该一元二次方程两个根的范围是﹣1<x1<0,2<x2<3,小李同学的这种方法主要运用的数学思想是( )
( http: / / www.21cnjy.com )
A.公理化 B.类比思想 C.数形结合 D.模型思想
5.(2018 葫芦岛质检)代数式ax2+bx+c(a≠0,a,b,c是常数)中,x与ax2+bx+c的对应值如下表:
x ﹣1 ﹣ ( http: / / www.21cnjy.com ) 0 ( http: / / www.21cnjy.com ) 1 ( http: / / www.21cnjy.com ) 2 ( http: / / www.21cnjy.com ) 3
ax2+bx+c ﹣2 ﹣ ( http: / / www.21cnjy.com ) 1 ( http: / / www.21cnjy.com ) 2 ( http: / / www.21cnjy.com ) 1 ﹣ ( http: / / www.21cnjy.com ) ﹣2
请判断一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1,x2的取值范围是下列选项中的( )
A.﹣ ( http: / / www.21cnjy.com )<x1<0, ( http: / / www.21cnjy.com )<x2<2 B.﹣1<x1<﹣ ( http: / / www.21cnjy.com ),2<x2< ( http: / / www.21cnjy.com )
C.﹣ ( http: / / www.21cnjy.com )<x1<0,2<x2< ( http: / / www.21cnjy.com ) D.﹣1<x1<﹣ ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )<x2<2
6.(2018 枣庄阴平中 ( http: / / www.21cnjy.com )学质检)小颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=﹣3.4,则方程的另一个近似根(精确到0.1)为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com )
A.4.4 B.3.4 C.2.4 D.1.4
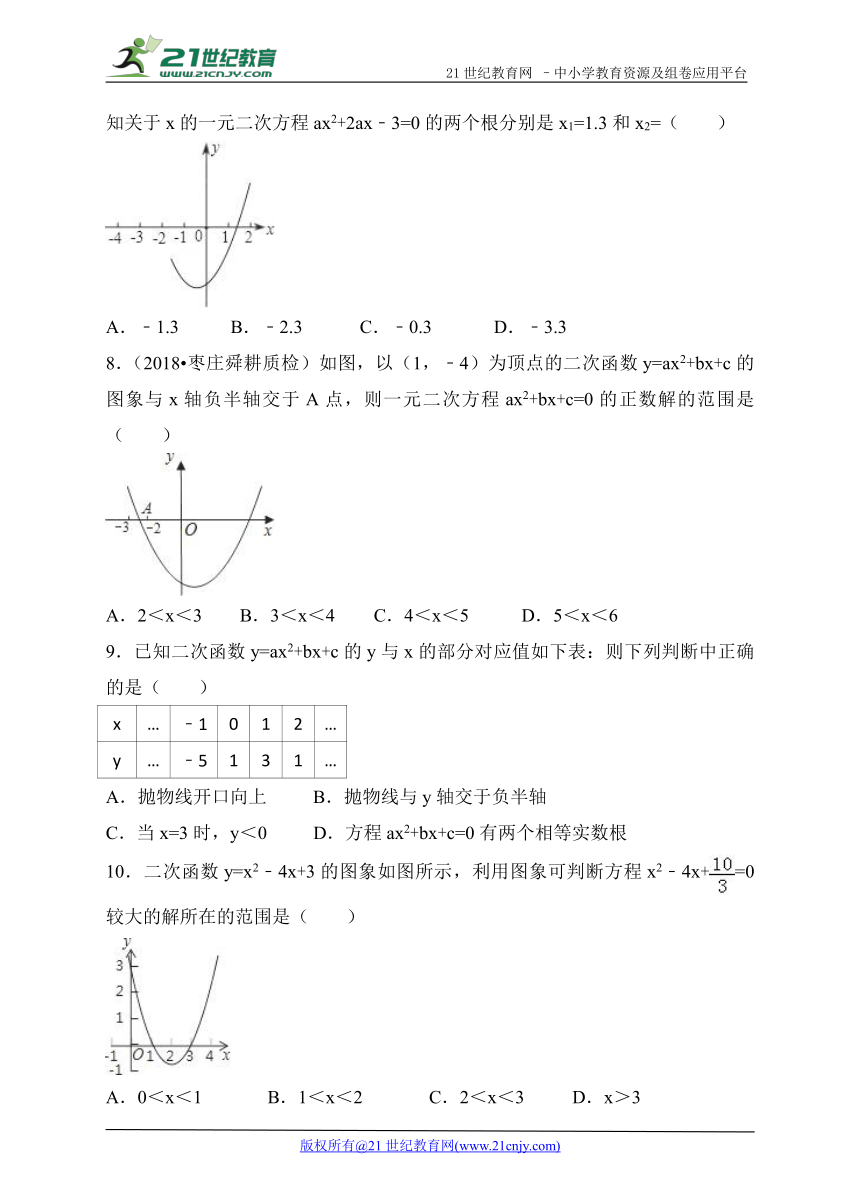
7.(2018 东营月考)已知二次函数 ( http: / / www.21cnjy.com )y=ax2+2ax﹣3的部分图象(如图),由图象可知关于x的一元二次方程ax2+2ax﹣3=0的两个根分别是x1=1.3和x2=( )
( http: / / www.21cnjy.com )
A.﹣1.3 B.﹣2.3 C.﹣0.3 D.﹣3.3
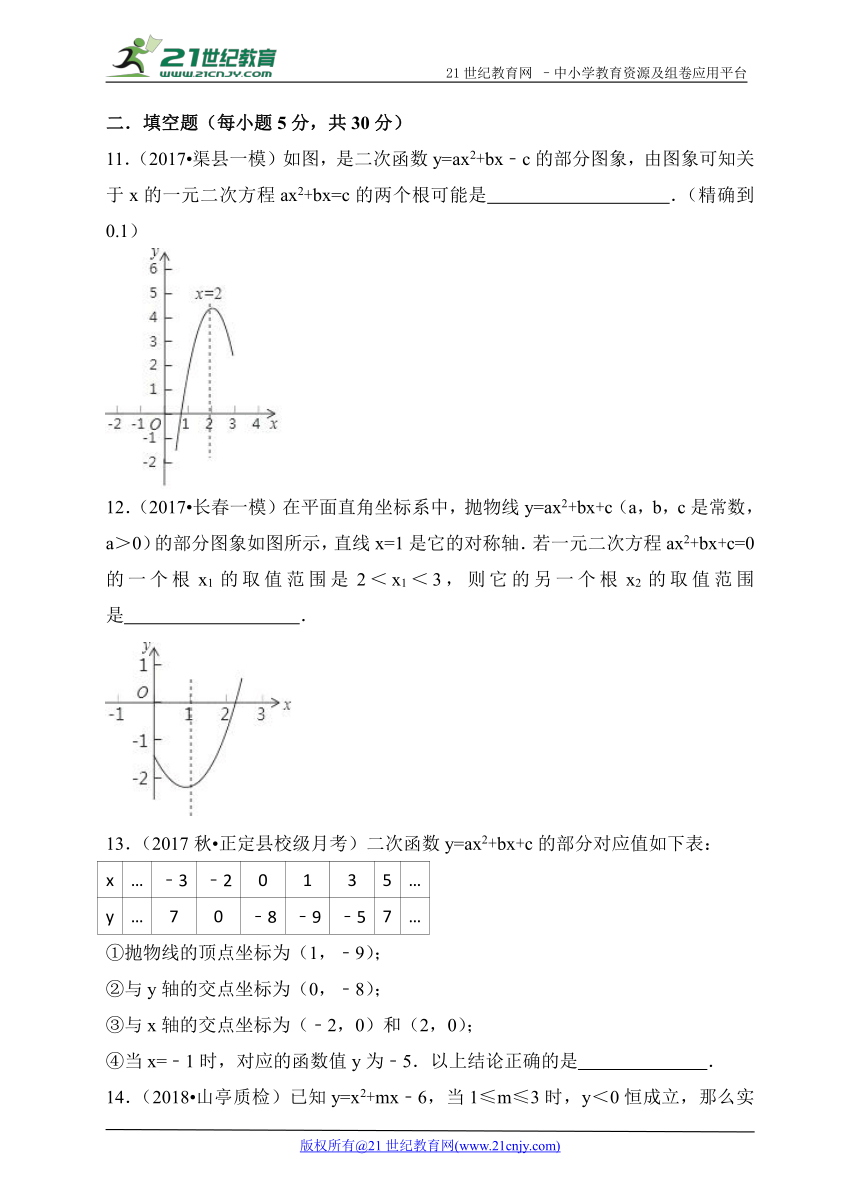
8.(2018 枣庄舜耕质检)如图 ( http: / / www.21cnjy.com ),以(1,﹣4)为顶点的二次函数y=ax2+bx+c的图象与x轴负半轴交于A点,则一元二次方程ax2+bx+c=0的正数解的范围是( )
( http: / / www.21cnjy.com )
A.2<x<3 B.3<x<4 C.4<x<5 D.5<x<6
9.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:则下列判断中正确的是( )
x … ﹣1 0 1 2 …
y … ﹣5 1 3 1 …
A.抛物线开口向上 B.抛物线与y轴交于负半轴
C.当x=3时,y<0 D.方程ax2+bx+c=0有两个相等实数根
10.二次函数y=x2﹣4x+3的图象如图所示,利用图象可判断方程x2﹣4x+ ( http: / / www.21cnjy.com )=0较大的解所在的范围是( )
( http: / / www.21cnjy.com )
A.0<x<1 B.1<x<2 C.2<x<3 D.x>3
二.填空题(每小题5分,共30分)
11.(2017 渠县一模)如图, ( http: / / www.21cnjy.com )是二次函数y=ax2+bx﹣c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是 .(精确到0.1)
( http: / / www.21cnjy.com )
12.(2017 长春一模)在平面直角坐标系 ( http: / / www.21cnjy.com )中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是 .
( http: / / www.21cnjy.com )
13.(2017秋 正定县校级月考)二次函数y=ax2+bx+c的部分对应值如下表:
x … ﹣3 ﹣2 0 1 3 5 …
y … 7 0 ﹣8 ﹣9 ﹣5 7 …
①抛物线的顶点坐标为(1,﹣9);
②与y轴的交点坐标为(0,﹣8);
③与x轴的交点坐标为(﹣2,0)和(2,0);
④当x=﹣1时,对应的函数值y为﹣5.以上结论正确的是 .
14.(2018 山亭质检)已知y=x2+mx﹣6,当1≤m≤3时,y<0恒成立,那么实数x的取值范围是 . 21教育网
15.二次函数的图象如图, ( http: / / www.21cnjy.com )对称轴为x=1.若关于x的一元二次方程x2+bx﹣t=0(为实数)在﹣1<x<4的范围内有解,则t的取值范围是 .
( http: / / www.21cnjy.com )
16.抛物线y=2x2﹣4x+m的图象的部分如图所示,则关于x的一元二次方程2x2﹣4x+m=0的解是 .21教育名师原创作品
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(10分)画出函数y=﹣2x2+8x﹣6的图象,根据图象回答:
(1)方程﹣2x2+8x﹣6=0的解是什么;
(2)当x取何值时,y>0;
(3)当x取何值时,y<0.
18.(10分)(201 ( http: / / www.21cnjy.com )7 云南)已知二次函数y=﹣2x2+bx+c图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.
(1)不等式b+2c+8≥0是否成立?请说明理由;
(2)设S是△AMO的面积,求满足S=9的所有点M的坐标.
2.5 二次函数与一元二次方程
第二课时检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017秋 新罗区校级期中)已知 ( http: / / www.21cnjy.com )一元二次方程1﹣(x﹣3)(x+2)=0,有两个实数根x1和x2,(x1<x2),则下列判断正确的是( )21世纪教育网版权所有
A.﹣2<x1<x2<3 B.x1<﹣2<3<x2 C.﹣2<x1<3<x2 D.x1<﹣2<x2<3
【分析】令y=(x﹣3)(x+2),由 ( http: / / www.21cnjy.com )1﹣(x﹣3)(x+2)=0的两根可看做抛物线y=(x﹣3)(x+2)与直线y=1交点的横坐标,根据函数图象可得答案.
【解答】解:令y=(x﹣3)(x+2),
当y=0时,(x﹣3)(x+2)=0,
则x=3或x=﹣2,
所以该抛物线与x轴的交点为(﹣2,0)和(3,0),
∵一元二次方程1﹣(x﹣3)(x+2)=0,
∴(x﹣3)(x+2)=1,
所以方程1﹣(x﹣3)(x+2)=0的两根可看做抛物线y=(x﹣3)(x+2)与直线y=1交点的横坐标,
其函数图象如下:
( http: / / www.21cnjy.com )
由函数图象可知,x1<﹣2<3<x2,
故选:B.
2.(2017 兰州)下表是一组二次函数y=x2+3x﹣5的自变量x与函数值y的对应值:
x 1 1.1 1.2 1.3 1.4
y ﹣1 ﹣0.49 0.04 0.59 1.16
那么方程x2+3x﹣5=0的一个近似根是( )
A.1 B.1.1 C.1.2 D.1.3
【分析】观察表格可得0.04更接近于0,得到所求方程的近似根即可.
【解答】解:观察表格得:方程x2+3x﹣5=0的一个近似根为1.2,
故选C
3.(2017 徐州模拟)二次函数 ( http: / / www.21cnjy.com )y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )21cnjy.com
( http: / / www.21cnjy.com )
A.t>﹣5 B.﹣5<t<3 C.3<t≤4 D.﹣5<t≤4
【分析】如图,关于x的一元二次方程﹣x2+mx﹣t=0的解就是抛物线y=﹣x2+mx与直线y=t的交点的横坐标,利用图象法即可解决问题.21·世纪*教育网
【解答】解:如图,关于x的一元二次方程﹣x2+mx﹣t=0的解就是抛物线y=﹣x2+mx与直线y=t的交点的横坐标,21*cnjy*com
( http: / / www.21cnjy.com )
当x=1时,y=3,
当x=5时,y=﹣5,
由图象可知关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,
直线y=t在直线y=﹣5和直线y=4之间包括直线y=4,
∴﹣5<t≤4.
故答案为D.
4.(2017 山西模拟)小李同学在求一 ( http: / / www.21cnjy.com )元二次方程﹣2x2+4x+1=0的近似根时,先在直角坐标系中使用软件绘制了二次函数y=﹣2x2+4x+1的图象(如图),接着观察图象与x轴的交点A和B的位置,然后得出该一元二次方程两个根的范围是﹣1<x1<0,2<x2<3,小李同学的这种方法主要运用的数学思想是( )
( http: / / www.21cnjy.com )
A.公理化 B.类比思想 C.数形结合 D.模型思想
【分析】结合图象解答题目,属于数形结合的数学思想.
【解答】解:根据函数解析式得到函数图象,结合函数图象得到抛物线与x轴交点的大体位置,属于数学结合的数学思想.
故选:C.
5.(2018 葫芦岛质检)代数式ax2+bx+c(a≠0,a,b,c是常数)中,x与ax2+bx+c的对应值如下表:
x ﹣1 ﹣ ( http: / / www.21cnjy.com ) 0 ( http: / / www.21cnjy.com ) 1 ( http: / / www.21cnjy.com ) 2 ( http: / / www.21cnjy.com ) 3
ax2+bx+c ﹣2 ﹣ ( http: / / www.21cnjy.com ) 1 ( http: / / www.21cnjy.com ) 2 ( http: / / www.21cnjy.com ) 1 ﹣ ( http: / / www.21cnjy.com ) ﹣2
请判断一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1,x2的取值范围是下列选项中的( )【来源:21·世纪·教育·网】
A.﹣ ( http: / / www.21cnjy.com )<x1<0, ( http: / / www.21cnjy.com )<x2<2 B.﹣1<x1<﹣ ( http: / / www.21cnjy.com ),2<x2< ( http: / / www.21cnjy.com )
C.﹣ ( http: / / www.21cnjy.com )<x1<0,2<x2< ( http: / / www.21cnjy.com ) D.﹣1<x1<﹣ ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )<x2<2
【分析】观察表格可知,在x<1时,随x值的增大,代数式ax2+bx+c的值逐渐增大,x的值在﹣ ( http: / / www.21cnjy.com )~0之间,代数式ax2+bx+c的值由负到正,故可判断ax2+bx+c=0时,对应的x的值在﹣ ( http: / / www.21cnjy.com )~0之间,在x>1时,随x的值增大,代数式ax2+bx+c逐渐减小,x的值在2~ ( http: / / www.21cnjy.com )之间,代数式ax2+bx+c的值由正到负,故可判断ax2+bx+c=0时,对应的x的值在2~ ( http: / / www.21cnjy.com )之间,21*cnjy*com
【解答】解:根据表格可知,代数式ax2+bx+c=0时,对应的x的值在﹣ ( http: / / www.21cnjy.com )~0和2~ ( http: / / www.21cnjy.com )之间,
即:一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1,x2的取值范围是﹣ ( http: / / www.21cnjy.com )<x1<0,2<x2< ( http: / / www.21cnjy.com )【出处:21教育名师】
故选C.
6.(2018 枣庄阴平中学质检)小 ( http: / / www.21cnjy.com )颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=﹣3.4,则方程的另一个近似根(精确到0.1)为( )
( http: / / www.21cnjy.com )
A.4.4 B.3.4 C.2.4 D.1.4
【分析】根据一元二次方程的一个近似根,得到抛物线与x轴的一个交点,根据抛物线的对称轴,求出另一个交点坐标,得到方程的另一个近似根.
【解答】解:∵抛物线与x轴的一个交点为(﹣3.4,0),又抛物线的对称轴为:x=﹣1,
∴另一个交点坐标为:(1.4,0),
则方程的另一个近似根为1.4,
故选:D.
7.(2018 东营月考)已知二次函数 ( http: / / www.21cnjy.com )y=ax2+2ax﹣3的部分图象(如图),由图象可知关于x的一元二次方程ax2+2ax﹣3=0的两个根分别是x1=1.3和x2=( )
( http: / / www.21cnjy.com )
A.﹣1.3 B.﹣2.3 C.﹣0.3 D.﹣3.3
【分析】根据解析式和图象与x轴的交点坐标关于对称轴对称,可得答案.
【解答】解:由二次函数y=ax2+2ax﹣3的部分图象,得
对称轴是x=﹣1,
x1与x2关于对称轴对称,结合图象可得
1.3﹣(﹣1)=﹣1﹣x2,
解得x2=﹣3.3.
故选:D.
8.(2018 枣庄舜耕质检) ( http: / / www.21cnjy.com )如图,以(1,﹣4)为顶点的二次函数y=ax2+bx+c的图象与x轴负半轴交于A点,则一元二次方程ax2+bx+c=0的正数解的范围是( )
( http: / / www.21cnjy.com )
A.2<x<3 B.3<x<4 C.4<x<5 D.5<x<6
【分析】先根据图象得出对称轴左侧图象与x轴交点横坐标的取值范围,再利用对称轴x=1,可以算出右侧交点横坐标的取值范围.
【解答】解:∵二次函数y=ax2+bx+c的顶点为(1,﹣4),
∴对称轴为x=1,
而对称轴左侧图象与x轴交点横坐标的取值范围是﹣3<x<﹣2,
∴右侧交点横坐标的取值范围是4<x<5.
故选:C.
9.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:则下列判断中正确的是( )
x … ﹣1 0 1 2 …
y … ﹣5 1 3 1 …
A.抛物线开口向上
B.抛物线与y轴交于负半轴
C.当x=3时,y<0
D.方程ax2+bx+c=0有两个相等实数根
【分析】结合图表可以得出当x=0或2时 ( http: / / www.21cnjy.com ),y=1,可以求出此函数的对称轴是x=1,顶点坐标为(1,3),借助(0,1)两点可求出二次函数解析式,从而得出抛物线的性质.
【解答】解:∵由图表可以得出当x=0或2时,y=1,可以求出此函数的对称轴是x=1,顶点坐标为(1,3),
∴二次函数解析式为:y=a(x﹣1)2+3,
再将(0,1)点代入得:1=a(﹣1)2+3,
解得:a=﹣2,
∴y=﹣2(x﹣1)2+3,
∵a<0
∴A,抛物线开口向上错误,故:A错误;
∵y=﹣2(x﹣1)2+3=﹣2x2+4x+1,
与y轴交点坐标为(0,1),故与y轴交于正半轴,
故:B错误;
∵x=3时,y=﹣5<0,
故:C正确;
∵方程ax2+bx+c=0,△=16+4×2×1=22>0,
此方程有两个不相等的实数根,
故:D.方程有两个相等实数根错误;
故选:C.
10.二次函数y=x2﹣4x+3的图象如图所示,利用图象可判断方程x2﹣4x+ ( http: / / www.21cnjy.com )=0较大的解所在的范围是( )
( http: / / www.21cnjy.com )
A.0<x<1 B.1<x<2 C.2<x<3 D.x>3
【分析】根据二次函数图象与直线y=﹣ ( http: / / www.21cnjy.com )的交点的横坐标是相应的一元二次方程x2﹣4x+ ( http: / / www.21cnjy.com )=0的解,可得方程x2﹣4x+ ( http: / / www.21cnjy.com )=0较大的解所在的范围.
【解答】解:由图象可知二次函数y=x2﹣4x+3的图象与直线y=﹣ ( http: / / www.21cnjy.com )的交点的较大的横坐标在2﹣3之间,
∴方程x2﹣4x+ ( http: / / www.21cnjy.com )=0较大的解所在的范围是2<x<3,
故选C.
二.填空题(每小题5分,共30分)
11.(2017 渠县一模)如图,是二次函 ( http: / / www.21cnjy.com )数y=ax2+bx﹣c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是 x1=0.8,x2=3.2合理即可 .(精确到0.1)
( http: / / www.21cnjy.com )
【分析】直接利用抛物线与x轴交点的位置估算出两根的大小.
【解答】解:由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是:x1=0.8,x2=3.2合理即可.
故答案为:x1=0.8,x2=3.2合理即可.
12.(2017 长春一模) ( http: / / www.21cnjy.com )在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是 ﹣1<x2<0 .
( http: / / www.21cnjy.com )
【分析】利用对称轴及二次函数的图象性质,可以把图象与x轴另一个交点的取值范围确定.
【解答】解:由图象可知x=2时,y<0;x=3时,y>0;
由于直线x=1是它的对称轴,则由二次函数图象的对称性可知:x=0时,y<0;x=﹣1时,y>0;
所以另一个根x2的取值范围为﹣1<x2<0.
故答案为:﹣1<x2<0.
13.(2017秋 正定县校级月考)二次函数y=ax2+bx+c的部分对应值如下表:
x … ﹣3 ﹣2 0 1 3 5 …
y … 7 0 ﹣8 ﹣9 ﹣5 7 …
①抛物线的顶点坐标为(1,﹣9);
②与y轴的交点坐标为(0,﹣8);
③与x轴的交点坐标为(﹣2,0)和(2,0);
④当x=﹣1时,对应的函数值y为﹣5.以上结论正确的是 ①②④ .
【分析】由上表得与y轴的交点坐标为(0 ( http: / / www.21cnjy.com ),﹣8);与x轴的一个交点坐标为(﹣2,0);函数图象有最低点(1,﹣9);有抛物线的对称性可得出可得出与x轴的另一个交点坐标为(4,0);当x=﹣1时,对应的函数值y为﹣5.从而可得出答案.21·cn·jy·com
【解答】解:根据上表可画出函数的图象,由图象可得,
①抛物线的顶点坐标为(1,﹣9);
②与y轴的交点坐标为(0,﹣8);
③与x轴的交点坐标为(﹣2,0)和(4,0);
④当x=﹣1时,对应的函数值y为﹣5.
故答案为:①②④.
14.(2018 山亭质检)已知y=x2+mx﹣6,当1≤m≤3时,y<0恒成立,那么实数x的取值范围是 ﹣3<x< ( http: / / www.21cnjy.com ) .【版权所有:21教育】
【分析】根据1≤m≤3,得出两个不等式 ( http: / / www.21cnjy.com ):当m=3时,x2+3x﹣6<0;当m=1时,x2+x﹣6=0;根据y<0,分别解不等式x2+3x﹣6<0,x2+x﹣6<0,可求实数x的取值范围.
【解答】解:
∵1≤m≤3,y<0,
∴当m=3时,x2+3x﹣6<0,
由y=x2+3x﹣6<0,
得 ( http: / / www.21cnjy.com )<x< ( http: / / www.21cnjy.com );
当m=1时,x2+x﹣6<0,
由y=x2+x﹣6<0,得﹣3<x<2.
∴实数x的取值范围为:﹣3<x< ( http: / / www.21cnjy.com ).
故本题答案为:﹣3<x< ( http: / / www.21cnjy.com ).
15.二次函数的图象如图,对称轴为x=1 ( http: / / www.21cnjy.com ).若关于x的一元二次方程x2+bx﹣t=0(为实数)在﹣1<x<4的范围内有解,则t的取值范围是 ﹣1≤t<8 .
( http: / / www.21cnjy.com )
【分析】根据对称轴求出b的值,从而得到x=﹣ ( http: / / www.21cnjy.com )1、4时的函数值,再根据一元二次方程x2+bx﹣t=0(t为实数)在﹣1<x<4的范围内有解相当于y=x2+bx与y=t在x的范围内有交点解答.2·1·c·n·j·y
【解答】解:对称轴为直线x=﹣ ( http: / / www.21cnjy.com )=1,
解得b=﹣2,
所以,二次函数解析式为y=x2﹣2x,
y=(x﹣1)2﹣1,
x=﹣1时,y=1+2=3,
x=4时,y=16﹣2×4=8,
∵x2+bx﹣t=0相当于y=x2+bx与直线y=t的交点的横坐标,
∴当﹣1≤t<8时,在﹣1<x<4的范围内有解.
故答案为:﹣1≤t<8.
( http: / / www.21cnjy.com )
16.抛物线y=2x2﹣4x+m的图象的部分如图所示,则关于x的一元二次方程2x2﹣4x+m=0的解是 x1=﹣1,x2=3 .2-1-c-n-j-y
( http: / / www.21cnjy.com )
【分析】由图象可知,抛物线y=2x2 ( http: / / www.21cnjy.com )﹣4x+m与x轴的一个交点为(﹣1,0),对称轴为x=1,根据抛物线的对称性可求抛物线与x轴的另一交点坐标,从而确定一元二次方程2x2﹣4x+m=0的解.
【解答】解:观察图象可知,抛物线y=2x2﹣4x+m与x轴的一个交点为(﹣1,0),对称轴为x=1,
∴抛物线与x轴的另一交点坐标为(3,0),
∴一元二次方程2x2﹣4x+m=0的解为x1=﹣1,x2=3.
故本题答案为:x1=﹣1,x2=3.
三.解答题(共20分)
17.(10分)画出函数y=﹣2x2+8x﹣6的图象,根据图象回答:
(1)方程﹣2x2+8x﹣6=0的解是什么;
(2)当x取何值时,y>0;
(3)当x取何值时,y<0.
【分析】利用描点连线的方法画出函数y=﹣2x2+8x﹣6的图象.再根据图象判断函数的增减性.
【解答】解:函数y=﹣2x2+8x﹣6的图象如图.由图象可知:
(1)方程﹣2x2+8x﹣6=0的解x1=1,x2=3.
(2)当1<x<3时,y>0.
(3)当x<1或x>3时,y<0.
( http: / / www.21cnjy.com )
18.(10分)(2017 云南)已知 ( http: / / www.21cnjy.com )二次函数y=﹣2x2+bx+c图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.【来源:21cnj*y.co*m】
(1)不等式b+2c+8≥0是否成立?请说明理由;
(2)设S是△AMO的面积,求满足S=9的所有点M的坐标.
【分析】(1)由题意可知抛物线的解析式为y=﹣2(x﹣3)2+8,由此求出b、c即可解决问题.
(2)设M(m,n),由题意 ( http: / / www.21cnjy.com ) 3 |n|=9,可得n=±6,分两种情形列出方程求出m的值即可;
【解答】解:(1)由题意抛物线的顶点坐标(3,8),
∴抛物线的解析式为y=﹣2(x﹣3)2+8=﹣2x2+12x﹣10,
∴b=12,c=﹣10,
∴b+2c+8=12﹣20+8=0,
∴不等式b+2c+8≥0成立.
(2)设M(m,n),
由题意 ( http: / / www.21cnjy.com ) 3 |n|=9,
∴n=±6,
①当n=6时,6=﹣2m2+12m﹣10,
解得m=2或4,
②当n=﹣6时,﹣6=﹣2m2+12m﹣10,
解得m=3± ( http: / / www.21cnjy.com ),
∴满足条件的点M的坐标为(2,6)或(4,6)或(3+ ( http: / / www.21cnjy.com ),﹣6)或(3﹣ ( http: / / www.21cnjy.com ),﹣6).
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
2.5 二次函数与一元二次方程
第二课时检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
1.(2017秋 新罗区校级期中)已知一 ( http: / / www.21cnjy.com )元二次方程1﹣(x﹣3)(x+2)=0,有两个实数根x1和x2,(x1<x2),则下列判断正确的是( )www.21-cn-jy.com
A.﹣2<x1<x2<3 B.x1<﹣2<3<x2
C.﹣2<x1<3<x2 D.x1<﹣2<x2<3
2.(2017 兰州)下表是一组二次函数y=x2+3x﹣5的自变量x与函数值y的对应值:
x 1 1.1 1.2 1.3 1.4
y ﹣1 ﹣0.49 0.04 0.59 1.16
那么方程x2+3x﹣5=0的一个近似根是( )
A.1 B.1.1 C.1.2 D.1.3
3.(2017 徐州模拟)二次函数y=﹣x ( http: / / www.21cnjy.com )2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
( http: / / www.21cnjy.com )
A.t>﹣5 B.﹣5<t<3 C.3<t≤4 D.﹣5<t≤4
4.(2017 山西模拟)小李同学在求一元 ( http: / / www.21cnjy.com )二次方程﹣2x2+4x+1=0的近似根时,先在直角坐标系中使用软件绘制了二次函数y=﹣2x2+4x+1的图象(如图),接着观察图象与x轴的交点A和B的位置,然后得出该一元二次方程两个根的范围是﹣1<x1<0,2<x2<3,小李同学的这种方法主要运用的数学思想是( )
( http: / / www.21cnjy.com )
A.公理化 B.类比思想 C.数形结合 D.模型思想
5.(2018 葫芦岛质检)代数式ax2+bx+c(a≠0,a,b,c是常数)中,x与ax2+bx+c的对应值如下表:
x ﹣1 ﹣ ( http: / / www.21cnjy.com ) 0 ( http: / / www.21cnjy.com ) 1 ( http: / / www.21cnjy.com ) 2 ( http: / / www.21cnjy.com ) 3
ax2+bx+c ﹣2 ﹣ ( http: / / www.21cnjy.com ) 1 ( http: / / www.21cnjy.com ) 2 ( http: / / www.21cnjy.com ) 1 ﹣ ( http: / / www.21cnjy.com ) ﹣2
请判断一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1,x2的取值范围是下列选项中的( )
A.﹣ ( http: / / www.21cnjy.com )<x1<0, ( http: / / www.21cnjy.com )<x2<2 B.﹣1<x1<﹣ ( http: / / www.21cnjy.com ),2<x2< ( http: / / www.21cnjy.com )
C.﹣ ( http: / / www.21cnjy.com )<x1<0,2<x2< ( http: / / www.21cnjy.com ) D.﹣1<x1<﹣ ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )<x2<2
6.(2018 枣庄阴平中 ( http: / / www.21cnjy.com )学质检)小颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=﹣3.4,则方程的另一个近似根(精确到0.1)为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com )
A.4.4 B.3.4 C.2.4 D.1.4
7.(2018 东营月考)已知二次函数 ( http: / / www.21cnjy.com )y=ax2+2ax﹣3的部分图象(如图),由图象可知关于x的一元二次方程ax2+2ax﹣3=0的两个根分别是x1=1.3和x2=( )
( http: / / www.21cnjy.com )
A.﹣1.3 B.﹣2.3 C.﹣0.3 D.﹣3.3
8.(2018 枣庄舜耕质检)如图 ( http: / / www.21cnjy.com ),以(1,﹣4)为顶点的二次函数y=ax2+bx+c的图象与x轴负半轴交于A点,则一元二次方程ax2+bx+c=0的正数解的范围是( )
( http: / / www.21cnjy.com )
A.2<x<3 B.3<x<4 C.4<x<5 D.5<x<6
9.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:则下列判断中正确的是( )
x … ﹣1 0 1 2 …
y … ﹣5 1 3 1 …
A.抛物线开口向上 B.抛物线与y轴交于负半轴
C.当x=3时,y<0 D.方程ax2+bx+c=0有两个相等实数根
10.二次函数y=x2﹣4x+3的图象如图所示,利用图象可判断方程x2﹣4x+ ( http: / / www.21cnjy.com )=0较大的解所在的范围是( )
( http: / / www.21cnjy.com )
A.0<x<1 B.1<x<2 C.2<x<3 D.x>3
二.填空题(每小题5分,共30分)
11.(2017 渠县一模)如图, ( http: / / www.21cnjy.com )是二次函数y=ax2+bx﹣c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是 .(精确到0.1)
( http: / / www.21cnjy.com )
12.(2017 长春一模)在平面直角坐标系 ( http: / / www.21cnjy.com )中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是 .
( http: / / www.21cnjy.com )
13.(2017秋 正定县校级月考)二次函数y=ax2+bx+c的部分对应值如下表:
x … ﹣3 ﹣2 0 1 3 5 …
y … 7 0 ﹣8 ﹣9 ﹣5 7 …
①抛物线的顶点坐标为(1,﹣9);
②与y轴的交点坐标为(0,﹣8);
③与x轴的交点坐标为(﹣2,0)和(2,0);
④当x=﹣1时,对应的函数值y为﹣5.以上结论正确的是 .
14.(2018 山亭质检)已知y=x2+mx﹣6,当1≤m≤3时,y<0恒成立,那么实数x的取值范围是 . 21教育网
15.二次函数的图象如图, ( http: / / www.21cnjy.com )对称轴为x=1.若关于x的一元二次方程x2+bx﹣t=0(为实数)在﹣1<x<4的范围内有解,则t的取值范围是 .
( http: / / www.21cnjy.com )
16.抛物线y=2x2﹣4x+m的图象的部分如图所示,则关于x的一元二次方程2x2﹣4x+m=0的解是 .21教育名师原创作品
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(10分)画出函数y=﹣2x2+8x﹣6的图象,根据图象回答:
(1)方程﹣2x2+8x﹣6=0的解是什么;
(2)当x取何值时,y>0;
(3)当x取何值时,y<0.
18.(10分)(201 ( http: / / www.21cnjy.com )7 云南)已知二次函数y=﹣2x2+bx+c图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.
(1)不等式b+2c+8≥0是否成立?请说明理由;
(2)设S是△AMO的面积,求满足S=9的所有点M的坐标.
2.5 二次函数与一元二次方程
第二课时检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017秋 新罗区校级期中)已知 ( http: / / www.21cnjy.com )一元二次方程1﹣(x﹣3)(x+2)=0,有两个实数根x1和x2,(x1<x2),则下列判断正确的是( )21世纪教育网版权所有
A.﹣2<x1<x2<3 B.x1<﹣2<3<x2 C.﹣2<x1<3<x2 D.x1<﹣2<x2<3
【分析】令y=(x﹣3)(x+2),由 ( http: / / www.21cnjy.com )1﹣(x﹣3)(x+2)=0的两根可看做抛物线y=(x﹣3)(x+2)与直线y=1交点的横坐标,根据函数图象可得答案.
【解答】解:令y=(x﹣3)(x+2),
当y=0时,(x﹣3)(x+2)=0,
则x=3或x=﹣2,
所以该抛物线与x轴的交点为(﹣2,0)和(3,0),
∵一元二次方程1﹣(x﹣3)(x+2)=0,
∴(x﹣3)(x+2)=1,
所以方程1﹣(x﹣3)(x+2)=0的两根可看做抛物线y=(x﹣3)(x+2)与直线y=1交点的横坐标,
其函数图象如下:
( http: / / www.21cnjy.com )
由函数图象可知,x1<﹣2<3<x2,
故选:B.
2.(2017 兰州)下表是一组二次函数y=x2+3x﹣5的自变量x与函数值y的对应值:
x 1 1.1 1.2 1.3 1.4
y ﹣1 ﹣0.49 0.04 0.59 1.16
那么方程x2+3x﹣5=0的一个近似根是( )
A.1 B.1.1 C.1.2 D.1.3
【分析】观察表格可得0.04更接近于0,得到所求方程的近似根即可.
【解答】解:观察表格得:方程x2+3x﹣5=0的一个近似根为1.2,
故选C
3.(2017 徐州模拟)二次函数 ( http: / / www.21cnjy.com )y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )21cnjy.com
( http: / / www.21cnjy.com )
A.t>﹣5 B.﹣5<t<3 C.3<t≤4 D.﹣5<t≤4
【分析】如图,关于x的一元二次方程﹣x2+mx﹣t=0的解就是抛物线y=﹣x2+mx与直线y=t的交点的横坐标,利用图象法即可解决问题.21·世纪*教育网
【解答】解:如图,关于x的一元二次方程﹣x2+mx﹣t=0的解就是抛物线y=﹣x2+mx与直线y=t的交点的横坐标,21*cnjy*com
( http: / / www.21cnjy.com )
当x=1时,y=3,
当x=5时,y=﹣5,
由图象可知关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,
直线y=t在直线y=﹣5和直线y=4之间包括直线y=4,
∴﹣5<t≤4.
故答案为D.
4.(2017 山西模拟)小李同学在求一 ( http: / / www.21cnjy.com )元二次方程﹣2x2+4x+1=0的近似根时,先在直角坐标系中使用软件绘制了二次函数y=﹣2x2+4x+1的图象(如图),接着观察图象与x轴的交点A和B的位置,然后得出该一元二次方程两个根的范围是﹣1<x1<0,2<x2<3,小李同学的这种方法主要运用的数学思想是( )
( http: / / www.21cnjy.com )
A.公理化 B.类比思想 C.数形结合 D.模型思想
【分析】结合图象解答题目,属于数形结合的数学思想.
【解答】解:根据函数解析式得到函数图象,结合函数图象得到抛物线与x轴交点的大体位置,属于数学结合的数学思想.
故选:C.
5.(2018 葫芦岛质检)代数式ax2+bx+c(a≠0,a,b,c是常数)中,x与ax2+bx+c的对应值如下表:
x ﹣1 ﹣ ( http: / / www.21cnjy.com ) 0 ( http: / / www.21cnjy.com ) 1 ( http: / / www.21cnjy.com ) 2 ( http: / / www.21cnjy.com ) 3
ax2+bx+c ﹣2 ﹣ ( http: / / www.21cnjy.com ) 1 ( http: / / www.21cnjy.com ) 2 ( http: / / www.21cnjy.com ) 1 ﹣ ( http: / / www.21cnjy.com ) ﹣2
请判断一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1,x2的取值范围是下列选项中的( )【来源:21·世纪·教育·网】
A.﹣ ( http: / / www.21cnjy.com )<x1<0, ( http: / / www.21cnjy.com )<x2<2 B.﹣1<x1<﹣ ( http: / / www.21cnjy.com ),2<x2< ( http: / / www.21cnjy.com )
C.﹣ ( http: / / www.21cnjy.com )<x1<0,2<x2< ( http: / / www.21cnjy.com ) D.﹣1<x1<﹣ ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )<x2<2
【分析】观察表格可知,在x<1时,随x值的增大,代数式ax2+bx+c的值逐渐增大,x的值在﹣ ( http: / / www.21cnjy.com )~0之间,代数式ax2+bx+c的值由负到正,故可判断ax2+bx+c=0时,对应的x的值在﹣ ( http: / / www.21cnjy.com )~0之间,在x>1时,随x的值增大,代数式ax2+bx+c逐渐减小,x的值在2~ ( http: / / www.21cnjy.com )之间,代数式ax2+bx+c的值由正到负,故可判断ax2+bx+c=0时,对应的x的值在2~ ( http: / / www.21cnjy.com )之间,21*cnjy*com
【解答】解:根据表格可知,代数式ax2+bx+c=0时,对应的x的值在﹣ ( http: / / www.21cnjy.com )~0和2~ ( http: / / www.21cnjy.com )之间,
即:一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1,x2的取值范围是﹣ ( http: / / www.21cnjy.com )<x1<0,2<x2< ( http: / / www.21cnjy.com )【出处:21教育名师】
故选C.
6.(2018 枣庄阴平中学质检)小 ( http: / / www.21cnjy.com )颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=﹣3.4,则方程的另一个近似根(精确到0.1)为( )
( http: / / www.21cnjy.com )
A.4.4 B.3.4 C.2.4 D.1.4
【分析】根据一元二次方程的一个近似根,得到抛物线与x轴的一个交点,根据抛物线的对称轴,求出另一个交点坐标,得到方程的另一个近似根.
【解答】解:∵抛物线与x轴的一个交点为(﹣3.4,0),又抛物线的对称轴为:x=﹣1,
∴另一个交点坐标为:(1.4,0),
则方程的另一个近似根为1.4,
故选:D.
7.(2018 东营月考)已知二次函数 ( http: / / www.21cnjy.com )y=ax2+2ax﹣3的部分图象(如图),由图象可知关于x的一元二次方程ax2+2ax﹣3=0的两个根分别是x1=1.3和x2=( )
( http: / / www.21cnjy.com )
A.﹣1.3 B.﹣2.3 C.﹣0.3 D.﹣3.3
【分析】根据解析式和图象与x轴的交点坐标关于对称轴对称,可得答案.
【解答】解:由二次函数y=ax2+2ax﹣3的部分图象,得
对称轴是x=﹣1,
x1与x2关于对称轴对称,结合图象可得
1.3﹣(﹣1)=﹣1﹣x2,
解得x2=﹣3.3.
故选:D.
8.(2018 枣庄舜耕质检) ( http: / / www.21cnjy.com )如图,以(1,﹣4)为顶点的二次函数y=ax2+bx+c的图象与x轴负半轴交于A点,则一元二次方程ax2+bx+c=0的正数解的范围是( )
( http: / / www.21cnjy.com )
A.2<x<3 B.3<x<4 C.4<x<5 D.5<x<6
【分析】先根据图象得出对称轴左侧图象与x轴交点横坐标的取值范围,再利用对称轴x=1,可以算出右侧交点横坐标的取值范围.
【解答】解:∵二次函数y=ax2+bx+c的顶点为(1,﹣4),
∴对称轴为x=1,
而对称轴左侧图象与x轴交点横坐标的取值范围是﹣3<x<﹣2,
∴右侧交点横坐标的取值范围是4<x<5.
故选:C.
9.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:则下列判断中正确的是( )
x … ﹣1 0 1 2 …
y … ﹣5 1 3 1 …
A.抛物线开口向上
B.抛物线与y轴交于负半轴
C.当x=3时,y<0
D.方程ax2+bx+c=0有两个相等实数根
【分析】结合图表可以得出当x=0或2时 ( http: / / www.21cnjy.com ),y=1,可以求出此函数的对称轴是x=1,顶点坐标为(1,3),借助(0,1)两点可求出二次函数解析式,从而得出抛物线的性质.
【解答】解:∵由图表可以得出当x=0或2时,y=1,可以求出此函数的对称轴是x=1,顶点坐标为(1,3),
∴二次函数解析式为:y=a(x﹣1)2+3,
再将(0,1)点代入得:1=a(﹣1)2+3,
解得:a=﹣2,
∴y=﹣2(x﹣1)2+3,
∵a<0
∴A,抛物线开口向上错误,故:A错误;
∵y=﹣2(x﹣1)2+3=﹣2x2+4x+1,
与y轴交点坐标为(0,1),故与y轴交于正半轴,
故:B错误;
∵x=3时,y=﹣5<0,
故:C正确;
∵方程ax2+bx+c=0,△=16+4×2×1=22>0,
此方程有两个不相等的实数根,
故:D.方程有两个相等实数根错误;
故选:C.
10.二次函数y=x2﹣4x+3的图象如图所示,利用图象可判断方程x2﹣4x+ ( http: / / www.21cnjy.com )=0较大的解所在的范围是( )
( http: / / www.21cnjy.com )
A.0<x<1 B.1<x<2 C.2<x<3 D.x>3
【分析】根据二次函数图象与直线y=﹣ ( http: / / www.21cnjy.com )的交点的横坐标是相应的一元二次方程x2﹣4x+ ( http: / / www.21cnjy.com )=0的解,可得方程x2﹣4x+ ( http: / / www.21cnjy.com )=0较大的解所在的范围.
【解答】解:由图象可知二次函数y=x2﹣4x+3的图象与直线y=﹣ ( http: / / www.21cnjy.com )的交点的较大的横坐标在2﹣3之间,
∴方程x2﹣4x+ ( http: / / www.21cnjy.com )=0较大的解所在的范围是2<x<3,
故选C.
二.填空题(每小题5分,共30分)
11.(2017 渠县一模)如图,是二次函 ( http: / / www.21cnjy.com )数y=ax2+bx﹣c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是 x1=0.8,x2=3.2合理即可 .(精确到0.1)
( http: / / www.21cnjy.com )
【分析】直接利用抛物线与x轴交点的位置估算出两根的大小.
【解答】解:由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是:x1=0.8,x2=3.2合理即可.
故答案为:x1=0.8,x2=3.2合理即可.
12.(2017 长春一模) ( http: / / www.21cnjy.com )在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是 ﹣1<x2<0 .
( http: / / www.21cnjy.com )
【分析】利用对称轴及二次函数的图象性质,可以把图象与x轴另一个交点的取值范围确定.
【解答】解:由图象可知x=2时,y<0;x=3时,y>0;
由于直线x=1是它的对称轴,则由二次函数图象的对称性可知:x=0时,y<0;x=﹣1时,y>0;
所以另一个根x2的取值范围为﹣1<x2<0.
故答案为:﹣1<x2<0.
13.(2017秋 正定县校级月考)二次函数y=ax2+bx+c的部分对应值如下表:
x … ﹣3 ﹣2 0 1 3 5 …
y … 7 0 ﹣8 ﹣9 ﹣5 7 …
①抛物线的顶点坐标为(1,﹣9);
②与y轴的交点坐标为(0,﹣8);
③与x轴的交点坐标为(﹣2,0)和(2,0);
④当x=﹣1时,对应的函数值y为﹣5.以上结论正确的是 ①②④ .
【分析】由上表得与y轴的交点坐标为(0 ( http: / / www.21cnjy.com ),﹣8);与x轴的一个交点坐标为(﹣2,0);函数图象有最低点(1,﹣9);有抛物线的对称性可得出可得出与x轴的另一个交点坐标为(4,0);当x=﹣1时,对应的函数值y为﹣5.从而可得出答案.21·cn·jy·com
【解答】解:根据上表可画出函数的图象,由图象可得,
①抛物线的顶点坐标为(1,﹣9);
②与y轴的交点坐标为(0,﹣8);
③与x轴的交点坐标为(﹣2,0)和(4,0);
④当x=﹣1时,对应的函数值y为﹣5.
故答案为:①②④.
14.(2018 山亭质检)已知y=x2+mx﹣6,当1≤m≤3时,y<0恒成立,那么实数x的取值范围是 ﹣3<x< ( http: / / www.21cnjy.com ) .【版权所有:21教育】
【分析】根据1≤m≤3,得出两个不等式 ( http: / / www.21cnjy.com ):当m=3时,x2+3x﹣6<0;当m=1时,x2+x﹣6=0;根据y<0,分别解不等式x2+3x﹣6<0,x2+x﹣6<0,可求实数x的取值范围.
【解答】解:
∵1≤m≤3,y<0,
∴当m=3时,x2+3x﹣6<0,
由y=x2+3x﹣6<0,
得 ( http: / / www.21cnjy.com )<x< ( http: / / www.21cnjy.com );
当m=1时,x2+x﹣6<0,
由y=x2+x﹣6<0,得﹣3<x<2.
∴实数x的取值范围为:﹣3<x< ( http: / / www.21cnjy.com ).
故本题答案为:﹣3<x< ( http: / / www.21cnjy.com ).
15.二次函数的图象如图,对称轴为x=1 ( http: / / www.21cnjy.com ).若关于x的一元二次方程x2+bx﹣t=0(为实数)在﹣1<x<4的范围内有解,则t的取值范围是 ﹣1≤t<8 .
( http: / / www.21cnjy.com )
【分析】根据对称轴求出b的值,从而得到x=﹣ ( http: / / www.21cnjy.com )1、4时的函数值,再根据一元二次方程x2+bx﹣t=0(t为实数)在﹣1<x<4的范围内有解相当于y=x2+bx与y=t在x的范围内有交点解答.2·1·c·n·j·y
【解答】解:对称轴为直线x=﹣ ( http: / / www.21cnjy.com )=1,
解得b=﹣2,
所以,二次函数解析式为y=x2﹣2x,
y=(x﹣1)2﹣1,
x=﹣1时,y=1+2=3,
x=4时,y=16﹣2×4=8,
∵x2+bx﹣t=0相当于y=x2+bx与直线y=t的交点的横坐标,
∴当﹣1≤t<8时,在﹣1<x<4的范围内有解.
故答案为:﹣1≤t<8.
( http: / / www.21cnjy.com )
16.抛物线y=2x2﹣4x+m的图象的部分如图所示,则关于x的一元二次方程2x2﹣4x+m=0的解是 x1=﹣1,x2=3 .2-1-c-n-j-y
( http: / / www.21cnjy.com )
【分析】由图象可知,抛物线y=2x2 ( http: / / www.21cnjy.com )﹣4x+m与x轴的一个交点为(﹣1,0),对称轴为x=1,根据抛物线的对称性可求抛物线与x轴的另一交点坐标,从而确定一元二次方程2x2﹣4x+m=0的解.
【解答】解:观察图象可知,抛物线y=2x2﹣4x+m与x轴的一个交点为(﹣1,0),对称轴为x=1,
∴抛物线与x轴的另一交点坐标为(3,0),
∴一元二次方程2x2﹣4x+m=0的解为x1=﹣1,x2=3.
故本题答案为:x1=﹣1,x2=3.
三.解答题(共20分)
17.(10分)画出函数y=﹣2x2+8x﹣6的图象,根据图象回答:
(1)方程﹣2x2+8x﹣6=0的解是什么;
(2)当x取何值时,y>0;
(3)当x取何值时,y<0.
【分析】利用描点连线的方法画出函数y=﹣2x2+8x﹣6的图象.再根据图象判断函数的增减性.
【解答】解:函数y=﹣2x2+8x﹣6的图象如图.由图象可知:
(1)方程﹣2x2+8x﹣6=0的解x1=1,x2=3.
(2)当1<x<3时,y>0.
(3)当x<1或x>3时,y<0.
( http: / / www.21cnjy.com )
18.(10分)(2017 云南)已知 ( http: / / www.21cnjy.com )二次函数y=﹣2x2+bx+c图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.【来源:21cnj*y.co*m】
(1)不等式b+2c+8≥0是否成立?请说明理由;
(2)设S是△AMO的面积,求满足S=9的所有点M的坐标.
【分析】(1)由题意可知抛物线的解析式为y=﹣2(x﹣3)2+8,由此求出b、c即可解决问题.
(2)设M(m,n),由题意 ( http: / / www.21cnjy.com ) 3 |n|=9,可得n=±6,分两种情形列出方程求出m的值即可;
【解答】解:(1)由题意抛物线的顶点坐标(3,8),
∴抛物线的解析式为y=﹣2(x﹣3)2+8=﹣2x2+12x﹣10,
∴b=12,c=﹣10,
∴b+2c+8=12﹣20+8=0,
∴不等式b+2c+8≥0成立.
(2)设M(m,n),
由题意 ( http: / / www.21cnjy.com ) 3 |n|=9,
∴n=±6,
①当n=6时,6=﹣2m2+12m﹣10,
解得m=2或4,
②当n=﹣6时,﹣6=﹣2m2+12m﹣10,
解得m=3± ( http: / / www.21cnjy.com ),
∴满足条件的点M的坐标为(2,6)或(4,6)或(3+ ( http: / / www.21cnjy.com ),﹣6)或(3﹣ ( http: / / www.21cnjy.com ),﹣6).
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
