云南省2017年高中学业水平考试模拟考(一)数学(文)试题+Word版含答案
文档属性
| 名称 | 云南省2017年高中学业水平考试模拟考(一)数学(文)试题+Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 460.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-25 09:47:13 | ||
图片预览



文档简介
绝密★启用前
2017年云南省高中学业水平考试模拟考(一)
文科数学试卷
学校:___________姓名:___________班级:___________考号:___________
题号
一
二
三
总分
得分
分卷I
一、选择题(共12小题,每小题5.0分,共60分)
1.设不等式组表示的平面区域为D.在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是( )
A.
B.
C.
D.
2.某化工厂单位要在600名员工中抽取60名员工调查职工身体健康状况,其中青年员工300名,中年员工200名,老年员工100名,下列说法错误的是( )
A. 老年人应作为重点调查对象,故老年人应该抽超过30名
B. 每个人被抽到的概率相同且为
C. 应使用分层抽样抽取样本调查
D. 抽出的样本能在一定程度上反应总体的健康状况
3.下列两个变量之间的关系是相关关系的是 ( )
A. 正方体的棱长和体积
B. 单位圆中角的度数和所对弧长
C. 单产为常数时,土地面积和总产量
D. 日照时间与水稻的亩产量
4.已知20名学生某次数学考试成绩(单位:分)的频率分布直方图如下图所示.则成绩落在[50,60)与[60,70)中的学生人数分别为( )
A. 2,3
B. 2,4
C. 3,2
D. 4,2
5.一个完整的程序框图至少包含( )
A. 起、止框和输入、输出框
B. 起、止框和处理框
C. 起、止框和判断框
D. 起、止框、处理框和输入、输出框
6.如图是某高中举办的2010年元旦学生歌曲大赛上,七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )
A. 84,85
B. 84,84
C. 85,84
D. 85,85
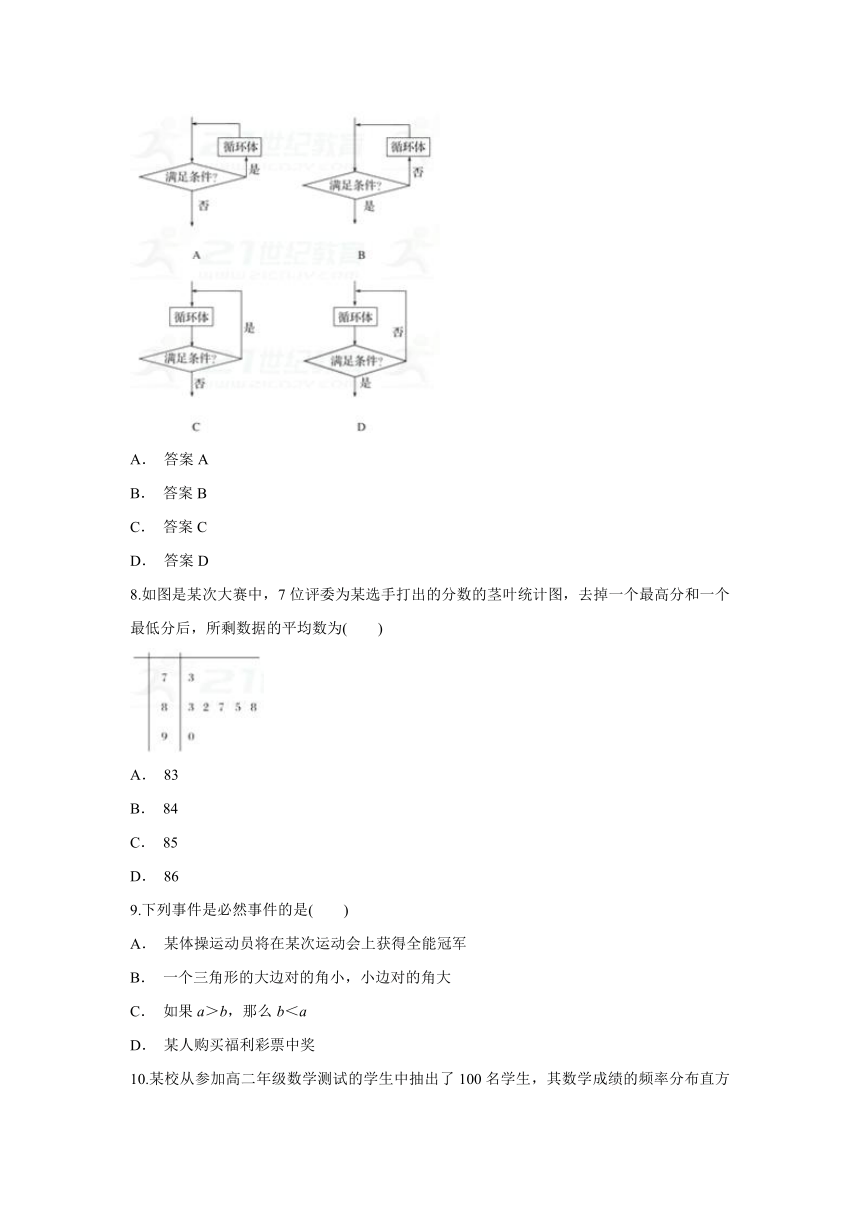
7.下列框图属于当型循环结构的是( )
A. 答案A
B. 答案B
C. 答案C
D. 答案D
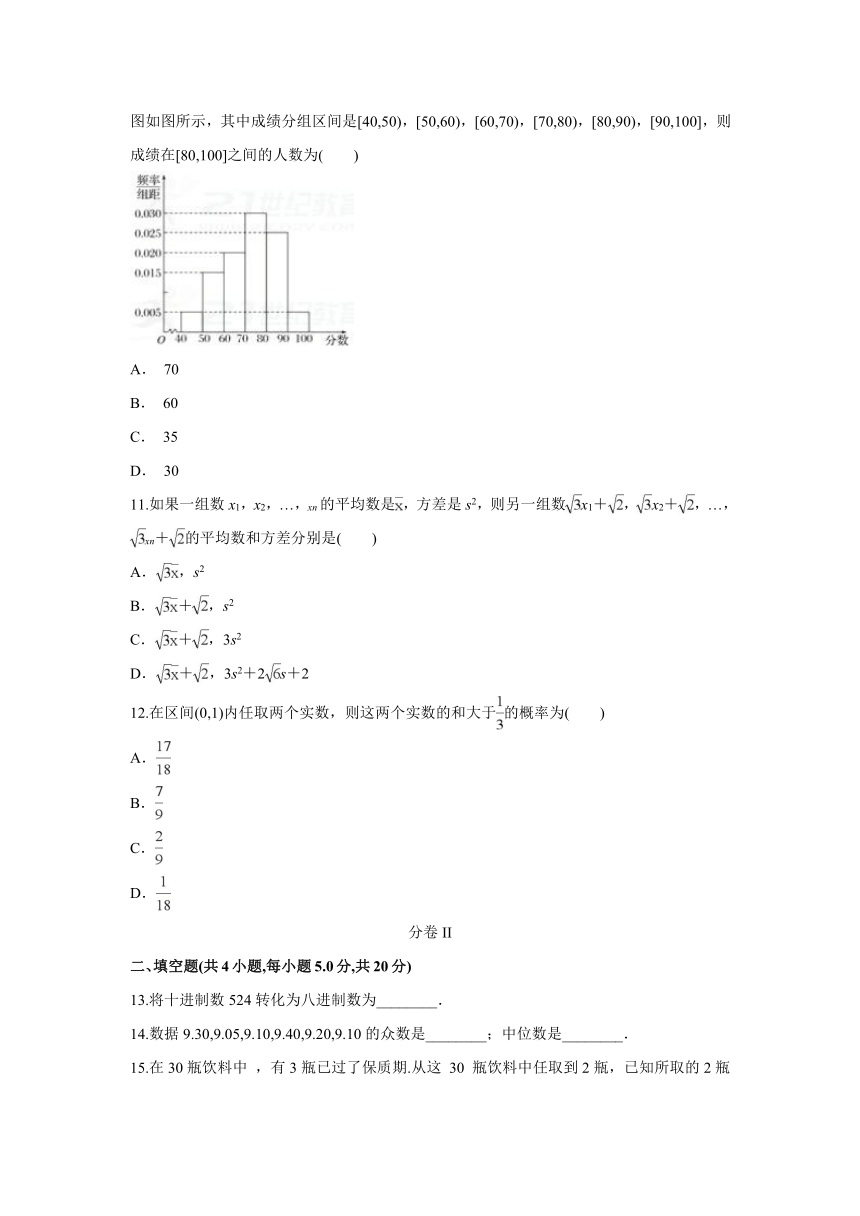
8.如图是某次大赛中,7位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数为( )
A. 83
B. 84
C. 85
D. 86
9.下列事件是必然事件的是( )
A. 某体操运动员将在某次运动会上获得全能冠军
B. 一个三角形的大边对的角小,小边对的角大
C. 如果a>b,那么b<a
D. 某人购买福利彩票中奖
10.某校从参加高二年级数学测试的学生中抽出了100名学生,其数学成绩的频率分布直方图如图所示,其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则成绩在[80,100]之间的人数为( )
A. 70
B. 60
C. 35
D. 30
11.如果一组数x1,x2,…,xn的平均数是,方差是s2,则另一组数x1+,x2+,…,xn+的平均数和方差分别是( )
A.,s2
B.+,s2
C.+,3s2
D.+,3s2+2s+2
12.在区间(0,1)内任取两个实数,则这两个实数的和大于的概率为( )
A.
B.
C.
D.
分卷II
二、填空题(共4小题,每小题5.0分,共20分)
13.将十进制数524转化为八进制数为________.
14.数据9.30,9.05,9.10,9.40,9.20,9.10的众数是________;中位数是________.
15.在30瓶饮料中 ,有3瓶已过了保质期.从这 30 瓶饮料中任取到2瓶,已知所取的2瓶全在保质期内的概率为,则至少取到1瓶已过保质期的概率为________.
16.程序:
若输入的是3,则运行结果是________.
三、解答题(共6小题,每小题12.0分,共72分)
17.给出30个数:1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,依次类推,要计算这30个数的和,现在已知该问题的算法的程序框图如图所示.
(1)请在图中判断框和处理框内填上合适的语句,使之能实现该题的算法功能;
(2)根据程序框图写出程序.
18.函数y=,写出给定自变量x,求函数值的算法.
19.以下是某次考试中某班15名同学的数学成绩:72,91,58,63,84,88,90,55,61,73,64,77,82,94,60.要求将80分以上的同学的平均分求出来.画出程序框图.
20.设有一个正方形网格,其中每个最小正方形的边长都为5 cm.现用直径为2 cm的硬币投掷到此网格上,求硬币落下后与格线有公共点的概率.
21.假定下述数据是甲、乙两个供货商的交货天数:
甲:10 9 10 10 11 11 9 11 10 10
乙:8 10 14 7 10 11 10 8 15 12
估计两个供货商的交货情况,并问哪个供货商交货时间短一些,哪个供货商交货时间较具一致性与可靠性.
22.某校随机抽取100名学生高中学业水平考试的X科成绩,并将成绩分成5组,得到频率分布表(部分)如下.
(1)直接写出频率分布表中①②③的值;
(2)如果每组学生的平均分都是分组端点的平均值(例如,第1组5个学生的平均分是=55),估计该校学生本次学业水平测试X科的平均分.
答案解析
1.【答案】D
【解析】由题意知此概型为几何概型,设所求事件为A,如图所示,边长为2的正方形区域为总度量μΩ,满足事件A的是阴影部分区域μA,故由几何概型的概率公式得,
P(A)==.
2.【答案】A
【解析】据样本特点,为了抽样的公平性,则应使用分层抽样,故A错误.
3.【答案】D
【解析】A项,由正方体的棱长和体积的公式知,V=a3(a>0),故A不对;
B项,单位圆中角的度数n和所对弧长l的关系为l=,故B不对;
C项,单产为常数k时,土地面积S和总产量L的关系为:L=k·S,故C不对;
D项,日照时间会影响水稻的亩产量,但不是唯一因素,它们之间有相关关系,故D对.
4.【答案】A
【解析】根据频率分布直方图,得,
(2a+3a+7a+6a+2a)×10=1,
解得a=0.005;
∴成绩落在[50,60)内的频率为
2a×10=0.1,
所求的学生人数为
20×0.1=2;
成绩落在[60,70)内的频率为
3a×10=0.15,
所求的学生人数为
20×0.15=3.
5.【答案】A
【解析】一个完整的程序框图至少需包括起、止框和输入、输出框.
6.【答案】A
【解析】去掉一个最高分和一个最低分后,
这组数据是84,85,86,84,87,
在这组数据中出现次数最多的是84,
∴众数是84,
把这组数据按照从小到大的顺序排列,最中间一个是85,
∴中位数是85.
7.【答案】A
【解析】当满足条件的时候执行循环体,故选A.
8.【答案】C
【解析】由茎叶图可知评委打出的最低分为73,最高分为90,去掉最高分和最低分,其余得分为83,82,87,85,88,
故平均分为=85.
9.【答案】C
【解析】选项A为随机事件,
选项B为不可能事件,
选项C为必然事件,
选项D为随机事件,
故选C.
10.【答案】D
【解析】成绩在[80,100]之间的频率为(0.005+0.025)×10=0.3,所以成绩在[80,100]之间的人数为0.3×100=30,故选D.
11.【答案】C
【解析】∵x1,x2,…,xn的平均数是,方差是s2,
∴x1+,x2+,…,xn+的平均数为+,
x1+,x2+,…,xn+的方差为3s2.
12.【答案】A
【解析】在区间(0,1)内任取的两个实数设为x,y,则对应的区域可表示为如图所示,两实数满足的区域为正方形区域OABC,两个实数的和大于满足的区域为五边形ABCDE,所以P两实数和大于===.
13.【答案】1 014(8)
【解析】524÷8=65…4,
65÷8=8…1,
8÷8=1…0,
∴化成八进制数是1 014(8).
14.【答案】9.10 9.15
【解析】出现次数最多的是9.10,故众数是9.10.将这些数按大小顺序排列,中间两个数为9.10,9.20,其平均数为=9.15,则中位数为9.15,故答案为9.10,9.15.
15.【答案】
【解析】事件“至少取到1瓶已过保质期的饮料”与事件“没有取到已过保质期的饮料”是对立事件,根据对立事件的概率公式得P=1-==.
16.【答案】12,3,18,54
【解析】对M,N进行赋值运算,第一句输入3时,将3赋给了M;第二句,将3赋给N;第三句,将12赋给M;第四句,将18赋给P;第五句,将54赋给Q;第六句,输出M,N,P,Q的值.
17.【答案】(1)该算法使用了当型循环结构,因为是求30个数的和,故循环体应执行30次,其中i是计数变量,因此判断框内的条件就是限制计数变量i的,故应为i≤30.算法中的变量p实质是表示参与求和的数,由于它也是变化的,且满足第i个数比其前一个数大i-1,第i+1个数比其前一个数大i,故处理框内应为p=p+i.故①处应填i≤30?;②处应填p=p+i.
(2)根据程序框图,可设计如下程序:
【解析】
18.【答案】算法如下:
第一步,输入x.
第二步,若x>0,则令y=-x+1后执行第五步,否则执行第三步.
第三步,若x=0,则令y=0后执行第五步,否则执行第四步.
第四步,令y=x+1.
第五步,输出y的值.
【解析】
19.【答案】用条件结构来判断成绩是否高于80分,用循环结构控制输入的次数,同时引进两个累加变量S、m,分别计算高于80分的成绩的总和S和人数m.
程序框图如图所示:
【解析】
20.【答案】记“硬币落下后与格线有公共点”为基本事件A,设共有n2(n∈N*)个边长为5 cm的正方形.如图所示,
当硬币的圆心落在正方形A1B1C1D1与ABCD之间的带形区域内部时,事件A发生.因为AB=5 cm,硬币半径为1 cm,所以A1B1=3 cm.因为共有n2个正方形,所以区域D=n2×52=25n2(cm2),区域d=n2×(52-32)=16n2(cm2),所以P(A)===.故硬币落下后与格线有公共点的概率为.
【解析】
21.【答案】解 甲=(10+9+10+10+11+11+9+11+10+10)=10.1,
乙=(8+10+14+7+10+11+10+8+15+12)
=10.5,
=[5×(10-10.1)2+2×(9-10.1)2+3×(11-10.1)2]=0.49,
=[3×(10-10.5)2+2×(8-10.5)2+(7-10.5)2+(11-10.5)2+(12-10.5)2+(14-10.5)2+(15-10.5)2]=6.05,
<.
所以甲供货商交货时间短一些,且交货时间具有一致性与可靠性.
【解析】
22.【答案】解 (1)从上至下,三个空依次是0.35×100=35,=0.30,1.00.
(2)第2、3、4、5组学生的平均分依次是=65;=75,=85,=95,
该校学生X科的平均分为
=74.5.
【解析】
2017年云南省高中学业水平考试模拟考(一)
文科数学试卷
学校:___________姓名:___________班级:___________考号:___________
题号
一
二
三
总分
得分
分卷I
一、选择题(共12小题,每小题5.0分,共60分)
1.设不等式组表示的平面区域为D.在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是( )
A.
B.
C.
D.
2.某化工厂单位要在600名员工中抽取60名员工调查职工身体健康状况,其中青年员工300名,中年员工200名,老年员工100名,下列说法错误的是( )
A. 老年人应作为重点调查对象,故老年人应该抽超过30名
B. 每个人被抽到的概率相同且为
C. 应使用分层抽样抽取样本调查
D. 抽出的样本能在一定程度上反应总体的健康状况
3.下列两个变量之间的关系是相关关系的是 ( )
A. 正方体的棱长和体积
B. 单位圆中角的度数和所对弧长
C. 单产为常数时,土地面积和总产量
D. 日照时间与水稻的亩产量
4.已知20名学生某次数学考试成绩(单位:分)的频率分布直方图如下图所示.则成绩落在[50,60)与[60,70)中的学生人数分别为( )
A. 2,3
B. 2,4
C. 3,2
D. 4,2
5.一个完整的程序框图至少包含( )
A. 起、止框和输入、输出框
B. 起、止框和处理框
C. 起、止框和判断框
D. 起、止框、处理框和输入、输出框
6.如图是某高中举办的2010年元旦学生歌曲大赛上,七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )
A. 84,85
B. 84,84
C. 85,84
D. 85,85
7.下列框图属于当型循环结构的是( )
A. 答案A
B. 答案B
C. 答案C
D. 答案D
8.如图是某次大赛中,7位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数为( )
A. 83
B. 84
C. 85
D. 86
9.下列事件是必然事件的是( )
A. 某体操运动员将在某次运动会上获得全能冠军
B. 一个三角形的大边对的角小,小边对的角大
C. 如果a>b,那么b<a
D. 某人购买福利彩票中奖
10.某校从参加高二年级数学测试的学生中抽出了100名学生,其数学成绩的频率分布直方图如图所示,其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则成绩在[80,100]之间的人数为( )
A. 70
B. 60
C. 35
D. 30
11.如果一组数x1,x2,…,xn的平均数是,方差是s2,则另一组数x1+,x2+,…,xn+的平均数和方差分别是( )
A.,s2
B.+,s2
C.+,3s2
D.+,3s2+2s+2
12.在区间(0,1)内任取两个实数,则这两个实数的和大于的概率为( )
A.
B.
C.
D.
分卷II
二、填空题(共4小题,每小题5.0分,共20分)
13.将十进制数524转化为八进制数为________.
14.数据9.30,9.05,9.10,9.40,9.20,9.10的众数是________;中位数是________.
15.在30瓶饮料中 ,有3瓶已过了保质期.从这 30 瓶饮料中任取到2瓶,已知所取的2瓶全在保质期内的概率为,则至少取到1瓶已过保质期的概率为________.
16.程序:
若输入的是3,则运行结果是________.
三、解答题(共6小题,每小题12.0分,共72分)
17.给出30个数:1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,依次类推,要计算这30个数的和,现在已知该问题的算法的程序框图如图所示.
(1)请在图中判断框和处理框内填上合适的语句,使之能实现该题的算法功能;
(2)根据程序框图写出程序.
18.函数y=,写出给定自变量x,求函数值的算法.
19.以下是某次考试中某班15名同学的数学成绩:72,91,58,63,84,88,90,55,61,73,64,77,82,94,60.要求将80分以上的同学的平均分求出来.画出程序框图.
20.设有一个正方形网格,其中每个最小正方形的边长都为5 cm.现用直径为2 cm的硬币投掷到此网格上,求硬币落下后与格线有公共点的概率.
21.假定下述数据是甲、乙两个供货商的交货天数:
甲:10 9 10 10 11 11 9 11 10 10
乙:8 10 14 7 10 11 10 8 15 12
估计两个供货商的交货情况,并问哪个供货商交货时间短一些,哪个供货商交货时间较具一致性与可靠性.
22.某校随机抽取100名学生高中学业水平考试的X科成绩,并将成绩分成5组,得到频率分布表(部分)如下.
(1)直接写出频率分布表中①②③的值;
(2)如果每组学生的平均分都是分组端点的平均值(例如,第1组5个学生的平均分是=55),估计该校学生本次学业水平测试X科的平均分.
答案解析
1.【答案】D
【解析】由题意知此概型为几何概型,设所求事件为A,如图所示,边长为2的正方形区域为总度量μΩ,满足事件A的是阴影部分区域μA,故由几何概型的概率公式得,
P(A)==.
2.【答案】A
【解析】据样本特点,为了抽样的公平性,则应使用分层抽样,故A错误.
3.【答案】D
【解析】A项,由正方体的棱长和体积的公式知,V=a3(a>0),故A不对;
B项,单位圆中角的度数n和所对弧长l的关系为l=,故B不对;
C项,单产为常数k时,土地面积S和总产量L的关系为:L=k·S,故C不对;
D项,日照时间会影响水稻的亩产量,但不是唯一因素,它们之间有相关关系,故D对.
4.【答案】A
【解析】根据频率分布直方图,得,
(2a+3a+7a+6a+2a)×10=1,
解得a=0.005;
∴成绩落在[50,60)内的频率为
2a×10=0.1,
所求的学生人数为
20×0.1=2;
成绩落在[60,70)内的频率为
3a×10=0.15,
所求的学生人数为
20×0.15=3.
5.【答案】A
【解析】一个完整的程序框图至少需包括起、止框和输入、输出框.
6.【答案】A
【解析】去掉一个最高分和一个最低分后,
这组数据是84,85,86,84,87,
在这组数据中出现次数最多的是84,
∴众数是84,
把这组数据按照从小到大的顺序排列,最中间一个是85,
∴中位数是85.
7.【答案】A
【解析】当满足条件的时候执行循环体,故选A.
8.【答案】C
【解析】由茎叶图可知评委打出的最低分为73,最高分为90,去掉最高分和最低分,其余得分为83,82,87,85,88,
故平均分为=85.
9.【答案】C
【解析】选项A为随机事件,
选项B为不可能事件,
选项C为必然事件,
选项D为随机事件,
故选C.
10.【答案】D
【解析】成绩在[80,100]之间的频率为(0.005+0.025)×10=0.3,所以成绩在[80,100]之间的人数为0.3×100=30,故选D.
11.【答案】C
【解析】∵x1,x2,…,xn的平均数是,方差是s2,
∴x1+,x2+,…,xn+的平均数为+,
x1+,x2+,…,xn+的方差为3s2.
12.【答案】A
【解析】在区间(0,1)内任取的两个实数设为x,y,则对应的区域可表示为如图所示,两实数满足的区域为正方形区域OABC,两个实数的和大于满足的区域为五边形ABCDE,所以P两实数和大于===.
13.【答案】1 014(8)
【解析】524÷8=65…4,
65÷8=8…1,
8÷8=1…0,
∴化成八进制数是1 014(8).
14.【答案】9.10 9.15
【解析】出现次数最多的是9.10,故众数是9.10.将这些数按大小顺序排列,中间两个数为9.10,9.20,其平均数为=9.15,则中位数为9.15,故答案为9.10,9.15.
15.【答案】
【解析】事件“至少取到1瓶已过保质期的饮料”与事件“没有取到已过保质期的饮料”是对立事件,根据对立事件的概率公式得P=1-==.
16.【答案】12,3,18,54
【解析】对M,N进行赋值运算,第一句输入3时,将3赋给了M;第二句,将3赋给N;第三句,将12赋给M;第四句,将18赋给P;第五句,将54赋给Q;第六句,输出M,N,P,Q的值.
17.【答案】(1)该算法使用了当型循环结构,因为是求30个数的和,故循环体应执行30次,其中i是计数变量,因此判断框内的条件就是限制计数变量i的,故应为i≤30.算法中的变量p实质是表示参与求和的数,由于它也是变化的,且满足第i个数比其前一个数大i-1,第i+1个数比其前一个数大i,故处理框内应为p=p+i.故①处应填i≤30?;②处应填p=p+i.
(2)根据程序框图,可设计如下程序:
【解析】
18.【答案】算法如下:
第一步,输入x.
第二步,若x>0,则令y=-x+1后执行第五步,否则执行第三步.
第三步,若x=0,则令y=0后执行第五步,否则执行第四步.
第四步,令y=x+1.
第五步,输出y的值.
【解析】
19.【答案】用条件结构来判断成绩是否高于80分,用循环结构控制输入的次数,同时引进两个累加变量S、m,分别计算高于80分的成绩的总和S和人数m.
程序框图如图所示:
【解析】
20.【答案】记“硬币落下后与格线有公共点”为基本事件A,设共有n2(n∈N*)个边长为5 cm的正方形.如图所示,
当硬币的圆心落在正方形A1B1C1D1与ABCD之间的带形区域内部时,事件A发生.因为AB=5 cm,硬币半径为1 cm,所以A1B1=3 cm.因为共有n2个正方形,所以区域D=n2×52=25n2(cm2),区域d=n2×(52-32)=16n2(cm2),所以P(A)===.故硬币落下后与格线有公共点的概率为.
【解析】
21.【答案】解 甲=(10+9+10+10+11+11+9+11+10+10)=10.1,
乙=(8+10+14+7+10+11+10+8+15+12)
=10.5,
=[5×(10-10.1)2+2×(9-10.1)2+3×(11-10.1)2]=0.49,
=[3×(10-10.5)2+2×(8-10.5)2+(7-10.5)2+(11-10.5)2+(12-10.5)2+(14-10.5)2+(15-10.5)2]=6.05,
<.
所以甲供货商交货时间短一些,且交货时间具有一致性与可靠性.
【解析】
22.【答案】解 (1)从上至下,三个空依次是0.35×100=35,=0.30,1.00.
(2)第2、3、4、5组学生的平均分依次是=65;=75,=85,=95,
该校学生X科的平均分为
=74.5.
【解析】
同课章节目录
