3.3 垂径定理一课一测
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
3.3 垂径定理检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
1.(2017秋 新罗区校级期中)如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )21*cnjy*com
( http: / / www.21cnjy.com )
A.2 ( http: / / www.21cnjy.com ) B.4 ( http: / / www.21cnjy.com )cm C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
2.(2017 黔西南州)如图,在⊙O中,半径OC与弦AB垂直于点D,且AB=8,OC=5,则CD的长是( )【版权所有:21教育】
( http: / / www.21cnjy.com )
A.3 B.2.5 C.2 D.1
3.(2017 西宁)如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.2 ( http: / / www.21cnjy.com ) C.2 ( http: / / www.21cnjy.com ) D.8
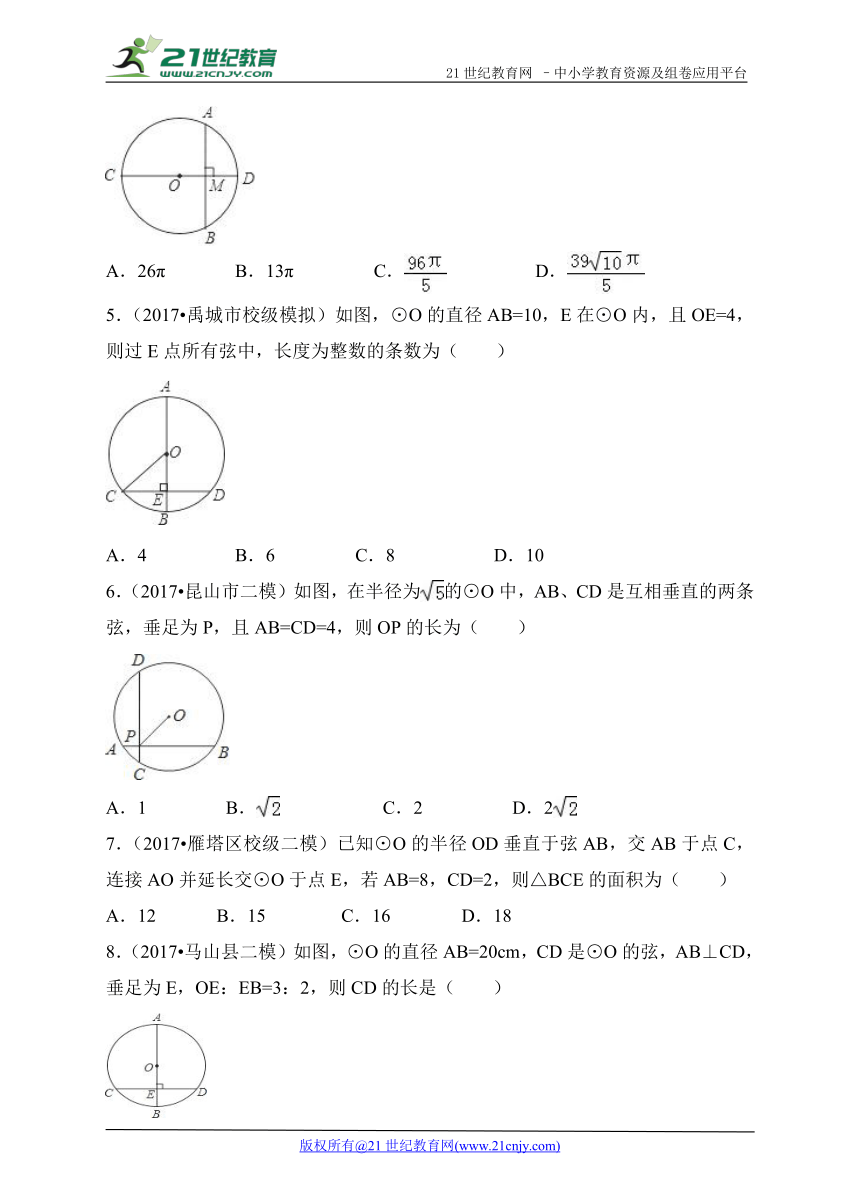
4.(2017 呼和浩特)如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )
( http: / / www.21cnjy.com )
A.26π B.13π C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
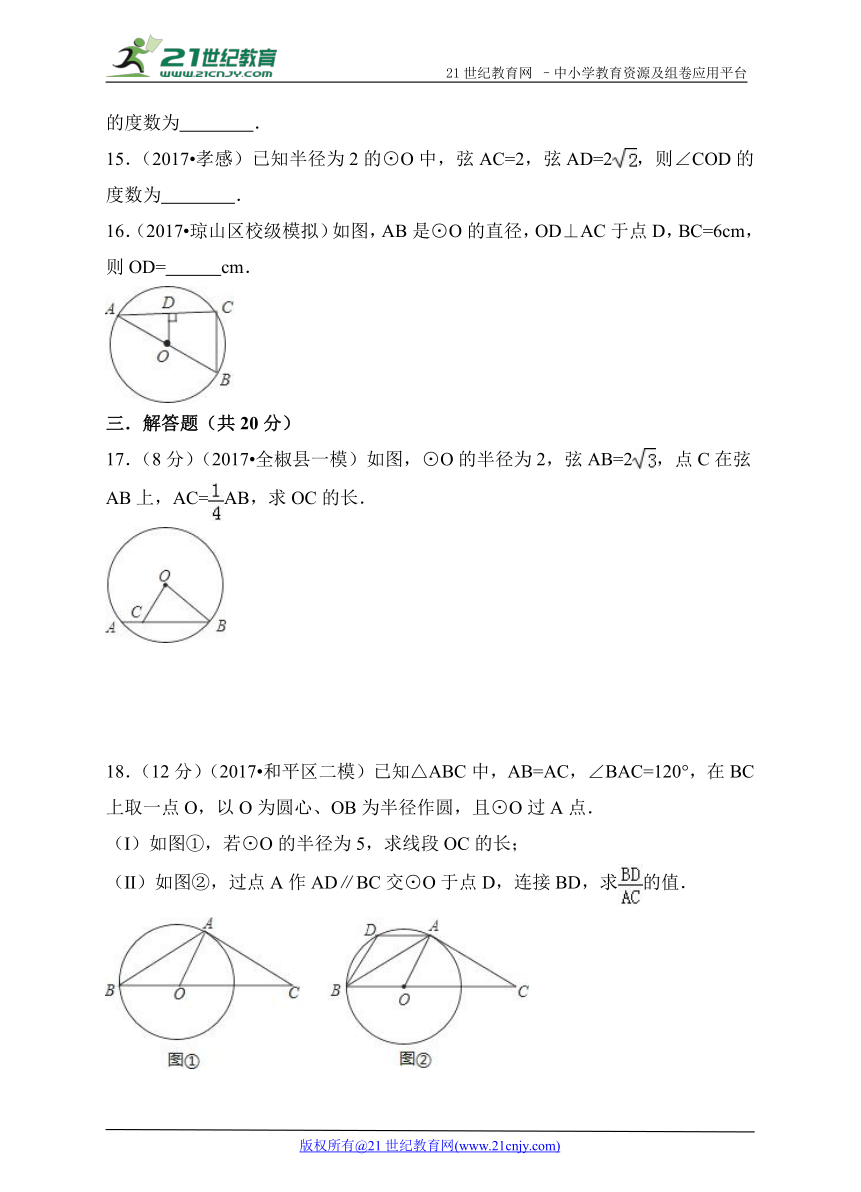
5.(2017 禹城市校级模拟)如图,⊙O的直径AB=10,E在⊙O内,且OE=4,则过E点所有弦中,长度为整数的条数为( )
( http: / / www.21cnjy.com )
A.4 B.6 C.8 D.10
6.(2017 昆山市二模)如图,在半径为 ( http: / / www.21cnjy.com )的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( )
( http: / / www.21cnjy.com )
A.1 B. ( http: / / www.21cnjy.com ) C.2 D.2 ( http: / / www.21cnjy.com )
7.(2017 雁塔区校级二模)已知⊙O ( http: / / www.21cnjy.com )的半径OD垂直于弦AB,交AB于点C,连接AO并延长交⊙O于点E,若AB=8,CD=2,则△BCE的面积为( )
A.12 B.15 C.16 D.18
8.(2017 马山县二模)如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
A.10cm B.14cm C.15cm D.16cm
9.(2017 顺德区一模)如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( )
( http: / / www.21cnjy.com )
A.3≤OM≤5 B.4≤OM≤5 C.3<OM<5 D.4<OM<5
10.(2017 武城县一模)已知⊙O的半径为2,点P是⊙O内一点,且OP= ( http: / / www.21cnjy.com ),过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
A.4 B.5 C.6 D.7
二.填空题(每小题5分,共30分)
11.(2017 舟山)如图,小明自制一块乒乓球拍,正面是半径为8cm的⊙O, ( http: / / www.21cnjy.com )=90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为 .
( http: / / www.21cnjy.com )
12.(2017 绥化模拟)在直径为150 ( http: / / www.21cnjy.com )cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度DC为30cm,那么油面宽度AB是 cm.
( http: / / www.21cnjy.com )
13.(2017 牡丹江)在半径为20的⊙O中,弦AB=32,点P在弦AB上,且OP=15,则AP= .
14.(2017 襄阳)在半径为1的⊙O中,弦AB、AC的长分别为1和 ( http: / / www.21cnjy.com ),则∠BAC的度数为 .
15.(2017 孝感)已知半径为2的⊙O中,弦AC=2,弦AD=2 ( http: / / www.21cnjy.com ),则∠COD的度数为 .
16.(2017 琼山区校级模拟)如图,AB是⊙O的直径,OD⊥AC于点D,BC=6cm,则OD= cm.
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(8分)(2017 全椒县一模)如图,⊙O的半径为2,弦AB=2 ( http: / / www.21cnjy.com ),点C在弦AB上,AC= ( http: / / www.21cnjy.com )AB,求OC的长.
( http: / / www.21cnjy.com )
18.(12分)(2017 和平区二模)已 ( http: / / www.21cnjy.com )知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点.
(Ⅰ)如图①,若⊙O的半径为5,求线段OC的长;
(Ⅱ)如图②,过点A作AD∥BC交⊙O于点D,连接BD,求 ( http: / / www.21cnjy.com )的值.
( http: / / www.21cnjy.com )
3.3 垂径定理检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017秋 新罗区校级期中)如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )21cnjy.com
( http: / / www.21cnjy.com )
A.2 ( http: / / www.21cnjy.com ) B.4 ( http: / / www.21cnjy.com )cm C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】连接AO,过O作OD⊥AB,交 ( http: / / www.21cnjy.com )于点D,交弦AB于点E,根据折叠的性质可知OE=DE,再根据垂径定理可知AE=BE,在Rt△AOE中利用勾股定理即可求出AE的长,进而可求出AB的长.www.21-cn-jy.com
【解答】解:如图所示,
连接AO,过O作OD⊥AB,交 ( http: / / www.21cnjy.com )于点D,交弦AB于点E,
∵ ( http: / / www.21cnjy.com )折叠后恰好经过圆心,
∴OE=DE,
∵⊙O的半径为4,
∴OE= ( http: / / www.21cnjy.com )OD= ( http: / / www.21cnjy.com )×4=2,
∵OD⊥AB,
∴AE= ( http: / / www.21cnjy.com )AB,
在Rt△AOE中,
AE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com ).
∴AB=2AE=4 ( http: / / www.21cnjy.com ).
故选B.
( http: / / www.21cnjy.com )
2.(2017 黔西南州)如图,在⊙O中,半径OC与弦AB垂直于点D,且AB=8,OC=5,则CD的长是( )
( http: / / www.21cnjy.com )
A.3 B.2.5 C.2 D.1
【分析】根据垂径定理以及勾股定理即可求答案.
【解答】解:连接OA,
设CD=x,
∵OA=OC=5,
∴OD=5﹣x,
∵OC⊥AB,
∴由垂径定理可知:AB=4,
由勾股定理可知:52=42+(5﹣x)2
∴x=2,
∴CD=2,
故选(C)
( http: / / www.21cnjy.com )
3.(2017 西宁)如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.2 ( http: / / www.21cnjy.com ) C.2 ( http: / / www.21cnjy.com ) D.8
【分析】作OH⊥CD于H,连结OC,如图,根据垂径定理由OH⊥CD得到HC=HD,再利用AP=2,BP=6可计算出半径OA=4,则OP=OA﹣AP=2,接着在Rt△OPH中根据含30度的直角三角形的性质计算出OH= ( http: / / www.21cnjy.com )OP=1,然后在Rt△OHC中利用勾股定理计算出CH= ( http: / / www.21cnjy.com ),所以CD=2CH=2 ( http: / / www.21cnjy.com ).
【解答】解:作OH⊥CD于H,连结OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=30°,
∴∠POH=60°,
∴OH= ( http: / / www.21cnjy.com )OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴CD=2CH=2 ( http: / / www.21cnjy.com ).
故选C.
( http: / / www.21cnjy.com )
4.(2017 呼和浩特)如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )
( http: / / www.21cnjy.com )
A.26π B.13π C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】连接OA,根据垂径定理得到AM= ( http: / / www.21cnjy.com )AB=6,设OM=5x,DM=8x,得到OA=OD=13x,根据勾股定理得到OA= ( http: / / www.21cnjy.com )×13,于是得到结论.
【解答】解:连接OA,
∵CD为⊙O的直径,弦AB⊥CD,
∴AM= ( http: / / www.21cnjy.com )AB=6,
∵OM:MD=5:8,
∴设OM=5x,DM=8x,
∴OA=OD=13x,
∴AM=12x=6,
∴x= ( http: / / www.21cnjy.com ),
∴OA= ( http: / / www.21cnjy.com )×13,
∴⊙O的周长=2OA π=13π,
故选B.
( http: / / www.21cnjy.com )
5.(2017 禹城市校级模拟)如图,⊙O的直径AB=10,E在⊙O内,且OE=4,则过E点所有弦中,长度为整数的条数为( )2-1-c-n-j-y
( http: / / www.21cnjy.com )
A.4 B.6 C.8 D.10
【分析】过E作CD⊥AB于 ( http: / / www.21cnjy.com )E,连接OC,则CD是过E的⊙O的最短的弦,AB是过E的⊙O的最长弦,根据勾股定理和垂径定理求出CD=6,得出弦的长度为6(1条),7、8、9(都有2条),10(1条),即可得出答案.
【解答】解:∵AB=10,
∵OB=OA=OC=5,
过E作CD⊥AB于E,连接OC,则CD是过E的⊙O的最短的弦,
∵OB⊥CD,
∴∠CEO=90°,
由勾股定理得:CE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=3,
∵OE⊥CD,OE过O,
∴CD=2CE=6,
∵AB是过E的⊙O的最长弦,AB=10,
∴过E点所有弦中,长度为整数的条数为1+2+2+2+1=8,
故选C.
6.(2017 昆山市二模)如图,在半径为 ( http: / / www.21cnjy.com )的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( )21教育名师原创作品
( http: / / www.21cnjy.com )
A.1 B. ( http: / / www.21cnjy.com ) C.2 D.2 ( http: / / www.21cnjy.com )
【分析】作OE⊥AB于E,OF⊥CD于F,连结OD、OB,如图,根据垂径定理得到AE=BE= ( http: / / www.21cnjy.com )AB=2,DF=CF= ( http: / / www.21cnjy.com )CD=2,根据勾股定理在Rt△OBE中计算出OE=1,同理可得OF=1,接着证明四边形OEPF为正方形,于是得到OP= ( http: / / www.21cnjy.com )OE= ( http: / / www.21cnjy.com ).
【解答】解:作OE⊥AB于E,OF⊥CD于F,连结OD、OB,如图,
则AE=BE= ( http: / / www.21cnjy.com )AB=2,DF=CF= ( http: / / www.21cnjy.com )CD=2,
在Rt△OBE中,∵OB= ( http: / / www.21cnjy.com ),BE=2,
∴OE= ( http: / / www.21cnjy.com )=1,
同理可得OF=1,
∵AB⊥CD,
∴四边形OEPF为矩形,
而OE=OF=1,
∴四边形OEPF为正方形,
∴OP= ( http: / / www.21cnjy.com )OE= ( http: / / www.21cnjy.com ).
故选B.
( http: / / www.21cnjy.com )
7.(2017 雁塔区校级二模)已知⊙ ( http: / / www.21cnjy.com )O的半径OD垂直于弦AB,交AB于点C,连接AO并延长交⊙O于点E,若AB=8,CD=2,则△BCE的面积为( )
A.12 B.15 C.16 D.18
【分析】设OC=x,根据垂径定理可 ( http: / / www.21cnjy.com )得出AC=4,利用勾股定理可得出关于x的一元二次方程,解方程求出x的值,进而得出OC的长度,再根据三角形的中位线的性质以及三角形的面积公式即可得出结论.【出处:21教育名师】
【解答】解:依照题意画出图形,如图所示.
设OC=x,则OA=OD=x+2,
∵OD⊥AB于C,
∴ ( http: / / www.21cnjy.com )
在Rt△OAC中,OC2+AC2=OA2,即x2+42=(x+2)2,
解得x=3,即OC=3,
∵OC为△ABE的中位线,
∴BE=2OC=6.
∵AE是⊙O的直径,
∴∠B=90°,
∴ ( http: / / www.21cnjy.com ).
故选A.
( http: / / www.21cnjy.com )
8.(2017 马山县二模)如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )
( http: / / www.21cnjy.com )
A.10cm B.14cm C.15cm D.16cm
【分析】根据垂径定理与勾股定理即可求出答案.
【解答】解:连接OC,
设OE=3x,EB=2x,
∴OB=OC=5x,
∵AB=20
∴10x=20
∴x=2,
∴由勾股定理可知:CE=4x=8,
∴CD=2CE=16
故选(D)
( http: / / www.21cnjy.com )
9.(2017 顺德区一模)如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( )2·1·c·n·j·y
( http: / / www.21cnjy.com )
A.3≤OM≤5 B.4≤OM≤5 C.3<OM<5 D.4<OM<5
【分析】由垂线段最短可知当OM⊥AB时最短,当OM是半径时最长.根据垂径定理求最短长度.
【解答】解:如图,连接OA,作OM⊥AB于M,
∵⊙O的直径为10,
∴半径为5,
∴OM的最大值为5,
∵OM⊥AB于M,
∴AM=BM,
∵AB=6,
∴AM=3,
在Rt△AOM中,OM= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=4;
此时OM最短,
当OM是半径时最长,OM=5.
所以OM长的取值范围是4≤OM≤5.
故选B.
( http: / / www.21cnjy.com )
10.(2017 武城县一模)已知⊙O的半径为2,点P是⊙O内一点,且OP= ( http: / / www.21cnjy.com ),过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
A.4 B.5 C.6 D.7
【分析】设出OE=x,利用勾股定理表示出AC,BD,用对角线互相垂直的四边形的面积的计算方法建立面积和OE的函数关系式,即可得出结论.
【解答】解:如图:
连接OA、OD,作OE⊥AC于E,OF⊥BD于F,
∵AC⊥BD,
∴四边形OEPF为矩形,
∵OA=OD=2,OP= ( http: / / www.21cnjy.com ),
设OE为x(x>0),
根据勾股定理得,OF=EP= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
在Rt△AOE中,AE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )
∴AC=2AE=2 ( http: / / www.21cnjy.com ),
同理得,BD=2DF=2 ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com ),
又∵任意对角线互相垂直的四边形的面积等于对角线乘积的 ( http: / / www.21cnjy.com ),
∴S四边形ABCD= ( http: / / www.21cnjy.com )AC×BD= ( http: / / www.21cnjy.com )×2 ( http: / / www.21cnjy.com )×2 ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com )
当x2= ( http: / / www.21cnjy.com )即:x= ( http: / / www.21cnjy.com )时,四边形ABCD的面积最大,等于2 ( http: / / www.21cnjy.com )=5.
故选:B.
( http: / / www.21cnjy.com )
二.填空题(每小题5分,共30分)
11.(2017 舟山)如图,小明自制一块乒乓球拍,正面是半径为8cm的⊙O, ( http: / / www.21cnjy.com )=90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为 (32+48π)cm2 .
( http: / / www.21cnjy.com )
【分析】连接OA、OB,根据三角形的面积公式求出S△AOB,根据扇形面积公式求出扇形ACB的面积,计算即可.21教育网
【解答】解:连接OA、OB,
∵ ( http: / / www.21cnjy.com )=90°,
∴∠AOB=90°,
∴S△AOB= ( http: / / www.21cnjy.com )×8×8=32,
扇形ACB(阴影部分)= ( http: / / www.21cnjy.com )=48π,
则弓形ACB胶皮面积为(32+48π)cm2,
故答案为:(32+48π)cm2.
( http: / / www.21cnjy.com )
12.(2017 绥化模拟)在直径 ( http: / / www.21cnjy.com )为150cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度DC为30cm,那么油面宽度AB是 120 cm.
( http: / / www.21cnjy.com )
【分析】在直角△OBD中利用勾股定理即可求得BD,然后根据垂径定理即可求得AB的长.
【解答】解:则OC⊥AB于点D,OC=OB= ( http: / / www.21cnjy.com )×150=75cm,OD=OC﹣CD=75﹣30=45cm.21·世纪*教育网
在直角△OBD中,BD= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=60(cm),
则AB=2BD=120cm.
故答案是:120.
13.(2017 牡丹江)在半径为20的⊙O中,弦AB=32,点P在弦AB上,且OP=15,则AP= 7或25 .21·cn·jy·com
【分析】作OC⊥AB于点C,根据垂径定理求出OC的长,根据勾股定理求出PC的长,分当点P在线段AC上和当点P在线段BC上两种情况计算即可.
【解答】解:作OC⊥AB于点C ( http: / / www.21cnjy.com ),
∴AC= ( http: / / www.21cnjy.com )AB=16,
OC= ( http: / / www.21cnjy.com )=12,又OP=15,
∴PC= ( http: / / www.21cnjy.com )=9,
当点P在线段AC上时,AP=16﹣9=7,
当点P在线段BC上时,AP=16+9=25.
故选:7或25.
14.(2017 襄阳)在半径为1的⊙O中,弦AB、AC的长分别为1和 ( http: / / www.21cnjy.com ),则∠BAC的度数为 15°或105° .www-2-1-cnjy-com
【分析】根据题意画出图形,作出辅助线,由于AC与AB在圆心的同侧还是异侧不能确定,故应分两种情况进行讨论.
【解答】解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.
∵OE⊥AC,OD⊥AB,
∴AE= ( http: / / www.21cnjy.com )AC= ( http: / / www.21cnjy.com ),AD= ( http: / / www.21cnjy.com )AB= ( http: / / www.21cnjy.com ),
∴sin∠AOE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),sin∠AOD= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴∠AOE=45°,∠AOD=30°,
∴∠BAO=60°,∠CAO=90°﹣45°=45°,
∴∠BAC=45°+60°=105°,或∠BAC′=60°﹣45°=15°.
∴∠BAC=15°或105°.
故答案是:15°或105°.
( http: / / www.21cnjy.com )
15.(2017 孝感)已知半径为2的⊙O中,弦AC=2,弦AD=2 ( http: / / www.21cnjy.com ),则∠COD的度数为 150°或30° .21世纪教育网版权所有
【分析】连接OC,过点O作OE⊥AD于点E, ( http: / / www.21cnjy.com )由OA=OC=AC可得出∠OAC=60°,再根据垂径定理结合勾股定理可得出AE=OE,即∠OAD=45°,利用角的计算结合圆周角与圆心角间的关系,即可求出∠COD的度数.21*cnjy*com
【解答】解:连接OC,过点O作OE⊥AD于点E,如图所示.
∵OA=OC=AC,
∴∠OAC=60°.
∵AD=2 ( http: / / www.21cnjy.com ),OE⊥AD,
∴AE= ( http: / / www.21cnjy.com ),OE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴∠OAD=45°,
∴∠CAD=∠OAC+∠OAD=105°或∠CAD=∠OAC﹣∠OAD=15°,
∴∠COD=360°﹣2×105°=150°或∠COD=2×15°=30°.
故答案为:150°或30°.
( http: / / www.21cnjy.com )
16.(2017 琼山区校级模拟)如图,AB是⊙O的直径,OD⊥AC于点D,BC=6cm,则OD= 3 cm.
( http: / / www.21cnjy.com )
【分析】先由垂径定理得出点D为AC的中点,则OD为△ABC的中位线,再根据三角形的中位线定理,即可求出OD的长.
【解答】解:∵OD⊥AC于点D,
∴AD=CD,
又∵OA=OB,
∴OD为△ABC的中位线,
∴OD= ( http: / / www.21cnjy.com )BC,
∵BC=6cm,
∴OD=3cm.
故答案为3.
三.解答题(共20分)
17.(8分)(2017 全椒县一模)如图,⊙O的半径为2,弦AB=2 ( http: / / www.21cnjy.com ),点C在弦AB上,AC= ( http: / / www.21cnjy.com )AB,求OC的长.
( http: / / www.21cnjy.com )
【分析】作OH⊥AB于H,根据垂径定理得AH=BH= ( http: / / www.21cnjy.com )AB= ( http: / / www.21cnjy.com ),再在Rt△BOH中,根据勾股定理得OH=1,由AC= ( http: / / www.21cnjy.com )AB得AC= ( http: / / www.21cnjy.com ),则CH=AH﹣AC= ( http: / / www.21cnjy.com ),然后根据勾股定理可计算出OC的长.
【解答】解:作OH⊥AB于H,如图,
∵OH⊥AB,
∴AH=BH,
∴AH=BH= ( http: / / www.21cnjy.com )AB= ( http: / / www.21cnjy.com )×2 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
在Rt△BOH中,OB=2,BH= ( http: / / www.21cnjy.com ),
∴OH= ( http: / / www.21cnjy.com )=1,
∵AC= ( http: / / www.21cnjy.com )AB= ( http: / / www.21cnjy.com )×2 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴CH=AH﹣AC= ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
在Rt△OHC中,OC= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
18.(12分)(2017 ( http: / / www.21cnjy.com ) 和平区二模)已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点.
(Ⅰ)如图①,若⊙O的半径为5,求线段OC的长;
(Ⅱ)如图②,过点A作AD∥BC交⊙O于点D,连接BD,求 ( http: / / www.21cnjy.com )的值.
( http: / / www.21cnjy.com )
【分析】(1)求出∠B=∠C=30°,求出∠AOC=60°,求出∠OAC=90°,得出OC=2OA即可.
(2)根据勾股定理求出AC,求出△BOD是等边三角形,求出AC= ( http: / / www.21cnjy.com )BD,即可求出答案.
【解答】解:(1)∵△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵OA=OB,
∴∠BAO=∠B=30°,
∴∠AOC=30°+30°=60°,
∴∠OAC=90°,
∵OA=5,
∴OC=2AO=10.
(2)连接OD,
∵∠AOC=60°,AD∥BC,
∴∠DAO=∠AOC=60°,
∵OD=OA,
∴∠ADO=60°,
∴∠DOB=∠ADO=60°,
∵OD=OB,
∴△DOB是等边三角形,
∴BD=OB=OA,
在Rt△OAC中,OC=2BD,由勾股定理得:AC= ( http: / / www.21cnjy.com )BD,
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
3.3 垂径定理检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
1.(2017秋 新罗区校级期中)如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )21*cnjy*com
( http: / / www.21cnjy.com )
A.2 ( http: / / www.21cnjy.com ) B.4 ( http: / / www.21cnjy.com )cm C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
2.(2017 黔西南州)如图,在⊙O中,半径OC与弦AB垂直于点D,且AB=8,OC=5,则CD的长是( )【版权所有:21教育】
( http: / / www.21cnjy.com )
A.3 B.2.5 C.2 D.1
3.(2017 西宁)如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.2 ( http: / / www.21cnjy.com ) C.2 ( http: / / www.21cnjy.com ) D.8
4.(2017 呼和浩特)如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )
( http: / / www.21cnjy.com )
A.26π B.13π C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
5.(2017 禹城市校级模拟)如图,⊙O的直径AB=10,E在⊙O内,且OE=4,则过E点所有弦中,长度为整数的条数为( )
( http: / / www.21cnjy.com )
A.4 B.6 C.8 D.10
6.(2017 昆山市二模)如图,在半径为 ( http: / / www.21cnjy.com )的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( )
( http: / / www.21cnjy.com )
A.1 B. ( http: / / www.21cnjy.com ) C.2 D.2 ( http: / / www.21cnjy.com )
7.(2017 雁塔区校级二模)已知⊙O ( http: / / www.21cnjy.com )的半径OD垂直于弦AB,交AB于点C,连接AO并延长交⊙O于点E,若AB=8,CD=2,则△BCE的面积为( )
A.12 B.15 C.16 D.18
8.(2017 马山县二模)如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
A.10cm B.14cm C.15cm D.16cm
9.(2017 顺德区一模)如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( )
( http: / / www.21cnjy.com )
A.3≤OM≤5 B.4≤OM≤5 C.3<OM<5 D.4<OM<5
10.(2017 武城县一模)已知⊙O的半径为2,点P是⊙O内一点,且OP= ( http: / / www.21cnjy.com ),过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
A.4 B.5 C.6 D.7
二.填空题(每小题5分,共30分)
11.(2017 舟山)如图,小明自制一块乒乓球拍,正面是半径为8cm的⊙O, ( http: / / www.21cnjy.com )=90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为 .
( http: / / www.21cnjy.com )
12.(2017 绥化模拟)在直径为150 ( http: / / www.21cnjy.com )cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度DC为30cm,那么油面宽度AB是 cm.
( http: / / www.21cnjy.com )
13.(2017 牡丹江)在半径为20的⊙O中,弦AB=32,点P在弦AB上,且OP=15,则AP= .
14.(2017 襄阳)在半径为1的⊙O中,弦AB、AC的长分别为1和 ( http: / / www.21cnjy.com ),则∠BAC的度数为 .
15.(2017 孝感)已知半径为2的⊙O中,弦AC=2,弦AD=2 ( http: / / www.21cnjy.com ),则∠COD的度数为 .
16.(2017 琼山区校级模拟)如图,AB是⊙O的直径,OD⊥AC于点D,BC=6cm,则OD= cm.
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(8分)(2017 全椒县一模)如图,⊙O的半径为2,弦AB=2 ( http: / / www.21cnjy.com ),点C在弦AB上,AC= ( http: / / www.21cnjy.com )AB,求OC的长.
( http: / / www.21cnjy.com )
18.(12分)(2017 和平区二模)已 ( http: / / www.21cnjy.com )知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点.
(Ⅰ)如图①,若⊙O的半径为5,求线段OC的长;
(Ⅱ)如图②,过点A作AD∥BC交⊙O于点D,连接BD,求 ( http: / / www.21cnjy.com )的值.
( http: / / www.21cnjy.com )
3.3 垂径定理检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017秋 新罗区校级期中)如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )21cnjy.com
( http: / / www.21cnjy.com )
A.2 ( http: / / www.21cnjy.com ) B.4 ( http: / / www.21cnjy.com )cm C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】连接AO,过O作OD⊥AB,交 ( http: / / www.21cnjy.com )于点D,交弦AB于点E,根据折叠的性质可知OE=DE,再根据垂径定理可知AE=BE,在Rt△AOE中利用勾股定理即可求出AE的长,进而可求出AB的长.www.21-cn-jy.com
【解答】解:如图所示,
连接AO,过O作OD⊥AB,交 ( http: / / www.21cnjy.com )于点D,交弦AB于点E,
∵ ( http: / / www.21cnjy.com )折叠后恰好经过圆心,
∴OE=DE,
∵⊙O的半径为4,
∴OE= ( http: / / www.21cnjy.com )OD= ( http: / / www.21cnjy.com )×4=2,
∵OD⊥AB,
∴AE= ( http: / / www.21cnjy.com )AB,
在Rt△AOE中,
AE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com ).
∴AB=2AE=4 ( http: / / www.21cnjy.com ).
故选B.
( http: / / www.21cnjy.com )
2.(2017 黔西南州)如图,在⊙O中,半径OC与弦AB垂直于点D,且AB=8,OC=5,则CD的长是( )
( http: / / www.21cnjy.com )
A.3 B.2.5 C.2 D.1
【分析】根据垂径定理以及勾股定理即可求答案.
【解答】解:连接OA,
设CD=x,
∵OA=OC=5,
∴OD=5﹣x,
∵OC⊥AB,
∴由垂径定理可知:AB=4,
由勾股定理可知:52=42+(5﹣x)2
∴x=2,
∴CD=2,
故选(C)
( http: / / www.21cnjy.com )
3.(2017 西宁)如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.2 ( http: / / www.21cnjy.com ) C.2 ( http: / / www.21cnjy.com ) D.8
【分析】作OH⊥CD于H,连结OC,如图,根据垂径定理由OH⊥CD得到HC=HD,再利用AP=2,BP=6可计算出半径OA=4,则OP=OA﹣AP=2,接着在Rt△OPH中根据含30度的直角三角形的性质计算出OH= ( http: / / www.21cnjy.com )OP=1,然后在Rt△OHC中利用勾股定理计算出CH= ( http: / / www.21cnjy.com ),所以CD=2CH=2 ( http: / / www.21cnjy.com ).
【解答】解:作OH⊥CD于H,连结OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=30°,
∴∠POH=60°,
∴OH= ( http: / / www.21cnjy.com )OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴CD=2CH=2 ( http: / / www.21cnjy.com ).
故选C.
( http: / / www.21cnjy.com )
4.(2017 呼和浩特)如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )
( http: / / www.21cnjy.com )
A.26π B.13π C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】连接OA,根据垂径定理得到AM= ( http: / / www.21cnjy.com )AB=6,设OM=5x,DM=8x,得到OA=OD=13x,根据勾股定理得到OA= ( http: / / www.21cnjy.com )×13,于是得到结论.
【解答】解:连接OA,
∵CD为⊙O的直径,弦AB⊥CD,
∴AM= ( http: / / www.21cnjy.com )AB=6,
∵OM:MD=5:8,
∴设OM=5x,DM=8x,
∴OA=OD=13x,
∴AM=12x=6,
∴x= ( http: / / www.21cnjy.com ),
∴OA= ( http: / / www.21cnjy.com )×13,
∴⊙O的周长=2OA π=13π,
故选B.
( http: / / www.21cnjy.com )
5.(2017 禹城市校级模拟)如图,⊙O的直径AB=10,E在⊙O内,且OE=4,则过E点所有弦中,长度为整数的条数为( )2-1-c-n-j-y
( http: / / www.21cnjy.com )
A.4 B.6 C.8 D.10
【分析】过E作CD⊥AB于 ( http: / / www.21cnjy.com )E,连接OC,则CD是过E的⊙O的最短的弦,AB是过E的⊙O的最长弦,根据勾股定理和垂径定理求出CD=6,得出弦的长度为6(1条),7、8、9(都有2条),10(1条),即可得出答案.
【解答】解:∵AB=10,
∵OB=OA=OC=5,
过E作CD⊥AB于E,连接OC,则CD是过E的⊙O的最短的弦,
∵OB⊥CD,
∴∠CEO=90°,
由勾股定理得:CE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=3,
∵OE⊥CD,OE过O,
∴CD=2CE=6,
∵AB是过E的⊙O的最长弦,AB=10,
∴过E点所有弦中,长度为整数的条数为1+2+2+2+1=8,
故选C.
6.(2017 昆山市二模)如图,在半径为 ( http: / / www.21cnjy.com )的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( )21教育名师原创作品
( http: / / www.21cnjy.com )
A.1 B. ( http: / / www.21cnjy.com ) C.2 D.2 ( http: / / www.21cnjy.com )
【分析】作OE⊥AB于E,OF⊥CD于F,连结OD、OB,如图,根据垂径定理得到AE=BE= ( http: / / www.21cnjy.com )AB=2,DF=CF= ( http: / / www.21cnjy.com )CD=2,根据勾股定理在Rt△OBE中计算出OE=1,同理可得OF=1,接着证明四边形OEPF为正方形,于是得到OP= ( http: / / www.21cnjy.com )OE= ( http: / / www.21cnjy.com ).
【解答】解:作OE⊥AB于E,OF⊥CD于F,连结OD、OB,如图,
则AE=BE= ( http: / / www.21cnjy.com )AB=2,DF=CF= ( http: / / www.21cnjy.com )CD=2,
在Rt△OBE中,∵OB= ( http: / / www.21cnjy.com ),BE=2,
∴OE= ( http: / / www.21cnjy.com )=1,
同理可得OF=1,
∵AB⊥CD,
∴四边形OEPF为矩形,
而OE=OF=1,
∴四边形OEPF为正方形,
∴OP= ( http: / / www.21cnjy.com )OE= ( http: / / www.21cnjy.com ).
故选B.
( http: / / www.21cnjy.com )
7.(2017 雁塔区校级二模)已知⊙ ( http: / / www.21cnjy.com )O的半径OD垂直于弦AB,交AB于点C,连接AO并延长交⊙O于点E,若AB=8,CD=2,则△BCE的面积为( )
A.12 B.15 C.16 D.18
【分析】设OC=x,根据垂径定理可 ( http: / / www.21cnjy.com )得出AC=4,利用勾股定理可得出关于x的一元二次方程,解方程求出x的值,进而得出OC的长度,再根据三角形的中位线的性质以及三角形的面积公式即可得出结论.【出处:21教育名师】
【解答】解:依照题意画出图形,如图所示.
设OC=x,则OA=OD=x+2,
∵OD⊥AB于C,
∴ ( http: / / www.21cnjy.com )
在Rt△OAC中,OC2+AC2=OA2,即x2+42=(x+2)2,
解得x=3,即OC=3,
∵OC为△ABE的中位线,
∴BE=2OC=6.
∵AE是⊙O的直径,
∴∠B=90°,
∴ ( http: / / www.21cnjy.com ).
故选A.
( http: / / www.21cnjy.com )
8.(2017 马山县二模)如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )
( http: / / www.21cnjy.com )
A.10cm B.14cm C.15cm D.16cm
【分析】根据垂径定理与勾股定理即可求出答案.
【解答】解:连接OC,
设OE=3x,EB=2x,
∴OB=OC=5x,
∵AB=20
∴10x=20
∴x=2,
∴由勾股定理可知:CE=4x=8,
∴CD=2CE=16
故选(D)
( http: / / www.21cnjy.com )
9.(2017 顺德区一模)如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( )2·1·c·n·j·y
( http: / / www.21cnjy.com )
A.3≤OM≤5 B.4≤OM≤5 C.3<OM<5 D.4<OM<5
【分析】由垂线段最短可知当OM⊥AB时最短,当OM是半径时最长.根据垂径定理求最短长度.
【解答】解:如图,连接OA,作OM⊥AB于M,
∵⊙O的直径为10,
∴半径为5,
∴OM的最大值为5,
∵OM⊥AB于M,
∴AM=BM,
∵AB=6,
∴AM=3,
在Rt△AOM中,OM= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=4;
此时OM最短,
当OM是半径时最长,OM=5.
所以OM长的取值范围是4≤OM≤5.
故选B.
( http: / / www.21cnjy.com )
10.(2017 武城县一模)已知⊙O的半径为2,点P是⊙O内一点,且OP= ( http: / / www.21cnjy.com ),过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
A.4 B.5 C.6 D.7
【分析】设出OE=x,利用勾股定理表示出AC,BD,用对角线互相垂直的四边形的面积的计算方法建立面积和OE的函数关系式,即可得出结论.
【解答】解:如图:
连接OA、OD,作OE⊥AC于E,OF⊥BD于F,
∵AC⊥BD,
∴四边形OEPF为矩形,
∵OA=OD=2,OP= ( http: / / www.21cnjy.com ),
设OE为x(x>0),
根据勾股定理得,OF=EP= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
在Rt△AOE中,AE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )
∴AC=2AE=2 ( http: / / www.21cnjy.com ),
同理得,BD=2DF=2 ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com ),
又∵任意对角线互相垂直的四边形的面积等于对角线乘积的 ( http: / / www.21cnjy.com ),
∴S四边形ABCD= ( http: / / www.21cnjy.com )AC×BD= ( http: / / www.21cnjy.com )×2 ( http: / / www.21cnjy.com )×2 ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com )
当x2= ( http: / / www.21cnjy.com )即:x= ( http: / / www.21cnjy.com )时,四边形ABCD的面积最大,等于2 ( http: / / www.21cnjy.com )=5.
故选:B.
( http: / / www.21cnjy.com )
二.填空题(每小题5分,共30分)
11.(2017 舟山)如图,小明自制一块乒乓球拍,正面是半径为8cm的⊙O, ( http: / / www.21cnjy.com )=90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为 (32+48π)cm2 .
( http: / / www.21cnjy.com )
【分析】连接OA、OB,根据三角形的面积公式求出S△AOB,根据扇形面积公式求出扇形ACB的面积,计算即可.21教育网
【解答】解:连接OA、OB,
∵ ( http: / / www.21cnjy.com )=90°,
∴∠AOB=90°,
∴S△AOB= ( http: / / www.21cnjy.com )×8×8=32,
扇形ACB(阴影部分)= ( http: / / www.21cnjy.com )=48π,
则弓形ACB胶皮面积为(32+48π)cm2,
故答案为:(32+48π)cm2.
( http: / / www.21cnjy.com )
12.(2017 绥化模拟)在直径 ( http: / / www.21cnjy.com )为150cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度DC为30cm,那么油面宽度AB是 120 cm.
( http: / / www.21cnjy.com )
【分析】在直角△OBD中利用勾股定理即可求得BD,然后根据垂径定理即可求得AB的长.
【解答】解:则OC⊥AB于点D,OC=OB= ( http: / / www.21cnjy.com )×150=75cm,OD=OC﹣CD=75﹣30=45cm.21·世纪*教育网
在直角△OBD中,BD= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=60(cm),
则AB=2BD=120cm.
故答案是:120.
13.(2017 牡丹江)在半径为20的⊙O中,弦AB=32,点P在弦AB上,且OP=15,则AP= 7或25 .21·cn·jy·com
【分析】作OC⊥AB于点C,根据垂径定理求出OC的长,根据勾股定理求出PC的长,分当点P在线段AC上和当点P在线段BC上两种情况计算即可.
【解答】解:作OC⊥AB于点C ( http: / / www.21cnjy.com ),
∴AC= ( http: / / www.21cnjy.com )AB=16,
OC= ( http: / / www.21cnjy.com )=12,又OP=15,
∴PC= ( http: / / www.21cnjy.com )=9,
当点P在线段AC上时,AP=16﹣9=7,
当点P在线段BC上时,AP=16+9=25.
故选:7或25.
14.(2017 襄阳)在半径为1的⊙O中,弦AB、AC的长分别为1和 ( http: / / www.21cnjy.com ),则∠BAC的度数为 15°或105° .www-2-1-cnjy-com
【分析】根据题意画出图形,作出辅助线,由于AC与AB在圆心的同侧还是异侧不能确定,故应分两种情况进行讨论.
【解答】解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.
∵OE⊥AC,OD⊥AB,
∴AE= ( http: / / www.21cnjy.com )AC= ( http: / / www.21cnjy.com ),AD= ( http: / / www.21cnjy.com )AB= ( http: / / www.21cnjy.com ),
∴sin∠AOE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),sin∠AOD= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴∠AOE=45°,∠AOD=30°,
∴∠BAO=60°,∠CAO=90°﹣45°=45°,
∴∠BAC=45°+60°=105°,或∠BAC′=60°﹣45°=15°.
∴∠BAC=15°或105°.
故答案是:15°或105°.
( http: / / www.21cnjy.com )
15.(2017 孝感)已知半径为2的⊙O中,弦AC=2,弦AD=2 ( http: / / www.21cnjy.com ),则∠COD的度数为 150°或30° .21世纪教育网版权所有
【分析】连接OC,过点O作OE⊥AD于点E, ( http: / / www.21cnjy.com )由OA=OC=AC可得出∠OAC=60°,再根据垂径定理结合勾股定理可得出AE=OE,即∠OAD=45°,利用角的计算结合圆周角与圆心角间的关系,即可求出∠COD的度数.21*cnjy*com
【解答】解:连接OC,过点O作OE⊥AD于点E,如图所示.
∵OA=OC=AC,
∴∠OAC=60°.
∵AD=2 ( http: / / www.21cnjy.com ),OE⊥AD,
∴AE= ( http: / / www.21cnjy.com ),OE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴∠OAD=45°,
∴∠CAD=∠OAC+∠OAD=105°或∠CAD=∠OAC﹣∠OAD=15°,
∴∠COD=360°﹣2×105°=150°或∠COD=2×15°=30°.
故答案为:150°或30°.
( http: / / www.21cnjy.com )
16.(2017 琼山区校级模拟)如图,AB是⊙O的直径,OD⊥AC于点D,BC=6cm,则OD= 3 cm.
( http: / / www.21cnjy.com )
【分析】先由垂径定理得出点D为AC的中点,则OD为△ABC的中位线,再根据三角形的中位线定理,即可求出OD的长.
【解答】解:∵OD⊥AC于点D,
∴AD=CD,
又∵OA=OB,
∴OD为△ABC的中位线,
∴OD= ( http: / / www.21cnjy.com )BC,
∵BC=6cm,
∴OD=3cm.
故答案为3.
三.解答题(共20分)
17.(8分)(2017 全椒县一模)如图,⊙O的半径为2,弦AB=2 ( http: / / www.21cnjy.com ),点C在弦AB上,AC= ( http: / / www.21cnjy.com )AB,求OC的长.
( http: / / www.21cnjy.com )
【分析】作OH⊥AB于H,根据垂径定理得AH=BH= ( http: / / www.21cnjy.com )AB= ( http: / / www.21cnjy.com ),再在Rt△BOH中,根据勾股定理得OH=1,由AC= ( http: / / www.21cnjy.com )AB得AC= ( http: / / www.21cnjy.com ),则CH=AH﹣AC= ( http: / / www.21cnjy.com ),然后根据勾股定理可计算出OC的长.
【解答】解:作OH⊥AB于H,如图,
∵OH⊥AB,
∴AH=BH,
∴AH=BH= ( http: / / www.21cnjy.com )AB= ( http: / / www.21cnjy.com )×2 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
在Rt△BOH中,OB=2,BH= ( http: / / www.21cnjy.com ),
∴OH= ( http: / / www.21cnjy.com )=1,
∵AC= ( http: / / www.21cnjy.com )AB= ( http: / / www.21cnjy.com )×2 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴CH=AH﹣AC= ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
在Rt△OHC中,OC= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
18.(12分)(2017 ( http: / / www.21cnjy.com ) 和平区二模)已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点.
(Ⅰ)如图①,若⊙O的半径为5,求线段OC的长;
(Ⅱ)如图②,过点A作AD∥BC交⊙O于点D,连接BD,求 ( http: / / www.21cnjy.com )的值.
( http: / / www.21cnjy.com )
【分析】(1)求出∠B=∠C=30°,求出∠AOC=60°,求出∠OAC=90°,得出OC=2OA即可.
(2)根据勾股定理求出AC,求出△BOD是等边三角形,求出AC= ( http: / / www.21cnjy.com )BD,即可求出答案.
【解答】解:(1)∵△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵OA=OB,
∴∠BAO=∠B=30°,
∴∠AOC=30°+30°=60°,
∴∠OAC=90°,
∵OA=5,
∴OC=2AO=10.
(2)连接OD,
∵∠AOC=60°,AD∥BC,
∴∠DAO=∠AOC=60°,
∵OD=OA,
∴∠ADO=60°,
∴∠DOB=∠ADO=60°,
∵OD=OB,
∴△DOB是等边三角形,
∴BD=OB=OA,
在Rt△OAC中,OC=2BD,由勾股定理得:AC= ( http: / / www.21cnjy.com )BD,
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
