3.6 直线和圆的位置关系(1)一课一测
文档属性
| 名称 | 3.6 直线和圆的位置关系(1)一课一测 |  | |
| 格式 | doc | ||
| 文件大小 | 794.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-26 13:55:38 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
3.6 直线和圆的位置关系
第一课时检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
1.(2017 百色)以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )www-2-1-cnjy-com
A.0≤b<2 ( http: / / www.21cnjy.com ) B.﹣2 ( http: / / www.21cnjy.com )
C.﹣2 ( http: / / www.21cnjy.com )2 ( http: / / www.21cnjy.com ) D.﹣2 ( http: / / www.21cnjy.com )<b<2 ( http: / / www.21cnjy.com )
2.(2017秋 海安县校级期中)已知⊙O和直线L相交,圆心到直线L的距离为10cm,则⊙O的半径可能为( )2-1-c-n-j-y
A.10cm B.6cm C.12cm D.以上都不对
3.(2017 市北区二模)⊙O的半径r=5cm,直线l到圆心O的距离d=4,则直线l与圆的位置关系( )
A.相离 B.相切 C.相交 D.重合
4.(2017 余杭区一模)在平面直角坐 ( http: / / www.21cnjy.com )标系xOy中,经过点(sin45°,cos30°)的直线,与以原点为圆心,2为半径的圆的位置关系是( )
A.相交 B.相切 C.相离 D.以上三者都有可能
5.(2017 徐州一模)如图,平面上⊙O ( http: / / www.21cnjy.com )与四条直线L1、L2、L3、L4的位置关系.若⊙O的半径为2cm,且O点到其中一条直线的距离为2.2cm,则这条直线是( )
( http: / / www.21cnjy.com )
A.Ll B.L2 C.L3 D.L4
6.(2017 阳谷县一模)已知等腰三角形 ( http: / / www.21cnjy.com )的腰长为6cm,底边长为4cm,以等腰三角形的顶角的顶点为圆心5cm为半径画圆,那么该圆与底边的位置关系是( )
A.相离 B.相切 C.相交 D.不能确定
7.(2017 茂县一模)已知⊙O的半径为3,圆心O到直线L的距离为2,则直线L与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
8.(2017 莱芜)如图 ( http: / / www.21cnjy.com ),AB是⊙O的直径,直线DA与⊙O相切于点A,DO交⊙O于点C,连接BC,若∠ABC=21°,则∠ADC的度数为( )
( http: / / www.21cnjy.com )
A.46° B.47° C.48° D.49°
9.(2017 吉林)如图,直线l是⊙ ( http: / / www.21cnjy.com )O的切线,A为切点,B为直线l上一点,连接OB交⊙O于点C.若AB=12,OA=5,则BC的长为( )
( http: / / www.21cnjy.com )
A.5 B.6 C.7 D.8
10.(2017 长春)如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )
( http: / / www.21cnjy.com )
A.29° B.32° C.42° D.58°
二.填空题(每小题5分,共30分)
11.(2017 江阴市二模)如图 ( http: / / www.21cnjy.com ),在Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上.则以MN为直径的圆与直线AB的位置关系是 .
( http: / / www.21cnjy.com )
12.(2016秋 徐州期末)若⊙O的半径为4cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系是 .21*cnjy*com
13.(2016秋 东台市期末)已 ( http: / / www.21cnjy.com )知点O到直线l的距离为6,以O为圆心,r为半径作⊙O,若⊙O上只有3个点到直线l的距离为2,则r的值为 .
14.(2017 黑龙江)如图,BD是⊙O的 ( http: / / www.21cnjy.com )切线,B为切点,连接DO与⊙O交于点C,AB为⊙O的直径,连接CA,若∠D=30°,⊙O的半径为4,则图中阴影部分的面积为 .
( http: / / www.21cnjy.com )
15.(2017 衢州)如图,在直角坐标系中,⊙A的圆心A的坐标为(﹣1,0),半径为1,点P为直线y=﹣ ( http: / / www.21cnjy.com )x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是 .
( http: / / www.21cnjy.com )
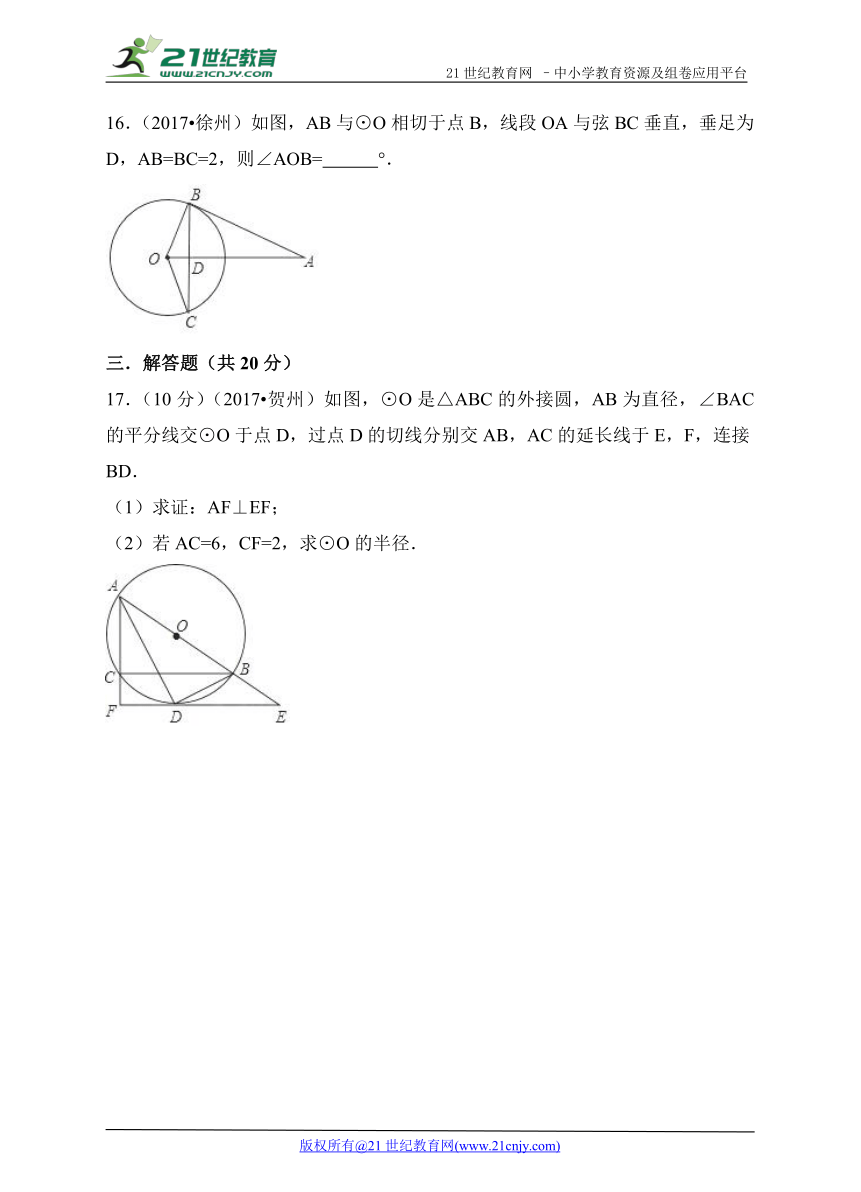
16.(2017 徐州)如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB= °.
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(10分)(2017 ( http: / / www.21cnjy.com ) 贺州)如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径.
( http: / / www.21cnjy.com )
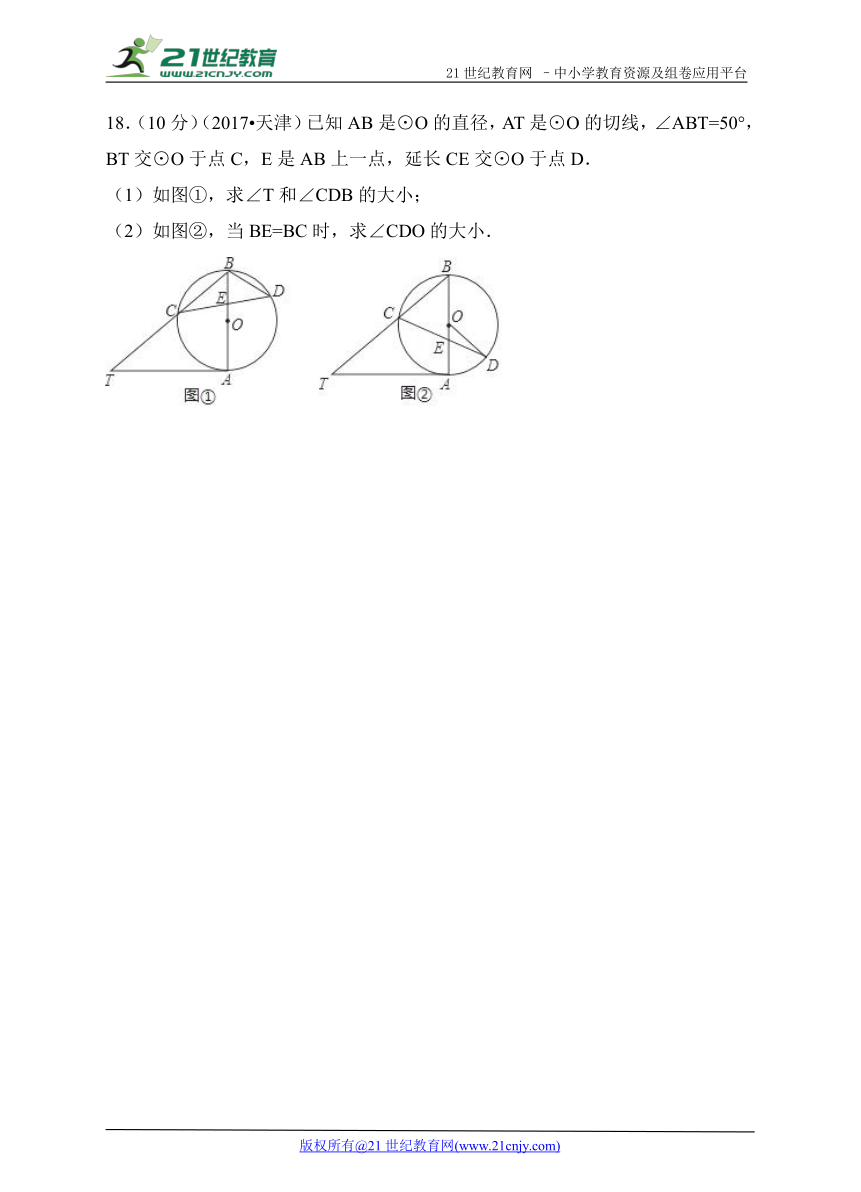
18.(10分)(201 ( http: / / www.21cnjy.com )7 天津)已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC时,求∠CDO的大小.
( http: / / www.21cnjy.com )
3.6 直线和圆的位置关系
第一课时检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017 百色)以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )
A.0≤b<2 ( http: / / www.21cnjy.com ) B.﹣2 ( http: / / www.21cnjy.com ) C.﹣2 ( http: / / www.21cnjy.com )2 ( http: / / www.21cnjy.com ) D.﹣2 ( http: / / www.21cnjy.com )<b<2 ( http: / / www.21cnjy.com )
【分析】求出直线y=﹣x+b与圆相切, ( http: / / www.21cnjy.com )且函数经过一、二、四象限,和当直线y=﹣x+b与圆相切,且函数经过二、三、四象限时b的值,则相交时b的值在相切时的两个b的值之间.
【解答】解:当直线y=﹣x+b与圆相切,且函数经过一、二、四象限时,如图.
在y=﹣x+b中,令x=0时,y=b,则与y轴的交点是(0,b),
当y=0时,x=b,则A的交点是(b,0),
则OA=OB,即△OAB是等腰直角三角形.
连接圆心O和切点C.则OC=2.
则OB= ( http: / / www.21cnjy.com )OC=2 ( http: / / www.21cnjy.com ).即b=2 ( http: / / www.21cnjy.com );
同理,当直线y=﹣x+b与圆相切,且函数经过二、三、四象限时,b=﹣2 ( http: / / www.21cnjy.com ).
则若直线y=﹣x+b与⊙O相交,则b的取值范围是﹣2 ( http: / / www.21cnjy.com )<b<2 ( http: / / www.21cnjy.com ).
故选D.
( http: / / www.21cnjy.com )
2.(2017秋 海安县校级期中)已知⊙O和直线L相交,圆心到直线L的距离为10cm,则⊙O的半径可能为( )2·1·c·n·j·y
A.10cm B.6cm C.12cm D.以上都不对
【分析】若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
【解答】解:∵⊙O和直线L相交,
∴d<r
∵d=10cm
∴r>10
∴只有选项C符合条件,
故选C.
3.(2017 市北区二模)⊙O的半径r=5cm,直线l到圆心O的距离d=4,则直线l与圆的位置关系( )21教育名师原创作品
A.相离 B.相切 C.相交 D.重合
【分析】由题意得出d<r,根据直线和圆的位置关系的判定方法判断即可.
【解答】解:∴⊙O的半径为5cm,如果圆心O到直线l的距离为4cm,
∴5>4,
即d<r,
∴直线l与⊙O的位置关系是相交,
故选C.
4.(2017 余杭区一模)在平面直角 ( http: / / www.21cnjy.com )坐标系xOy中,经过点(sin45°,cos30°)的直线,与以原点为圆心,2为半径的圆的位置关系是( )
A.相交 B.相切
C.相离 D.以上三者都有可能
【分析】设直线经过的点为A,若点A ( http: / / www.21cnjy.com )在圆内则直线和圆一定相交;若点在圆上或圆外则直线和圆有可能相交或相切或相离,所以先要计算OA的长和半径2比较大小再做选择.21教育网
【解答】解:设直线经过的点为A,
∵点A的坐标为(sin45°,cos30°),
∴OA= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∵圆的半径为2,
∴OA<2,
∴点A在圆内,
∴直线和圆一定相交,
故选A.
( http: / / www.21cnjy.com )
5.(2017 徐州一模)如图,平面上⊙ ( http: / / www.21cnjy.com )O与四条直线L1、L2、L3、L4的位置关系.若⊙O的半径为2cm,且O点到其中一条直线的距离为2.2cm,则这条直线是( )
( http: / / www.21cnjy.com )
A.Ll B.L2 C.L3 D.L4
【分析】根据直线和圆的位置关系与数量 ( http: / / www.21cnjy.com )之间的联系:当d=r,则直线和圆相切;当d<r,则直线和圆相交;当d>r,则直线和圆相离,进行分析判断.
【解答】解:因为所求直线到圆心O点的距离为2.2cm>半径2cm,
所以此直线与圆O相离,即为直线l3.
故选C.
6.(2017 阳谷县一模)已知等腰三 ( http: / / www.21cnjy.com )角形的腰长为6cm,底边长为4cm,以等腰三角形的顶角的顶点为圆心5cm为半径画圆,那么该圆与底边的位置关系是( )
A.相离 B.相切 C.相交 D.不能确定
【分析】作AD⊥BC于D,由等腰三角形的性质得出BD=CD= ( http: / / www.21cnjy.com )BC=2,由勾股定理求出AD=4 ( http: / / www.21cnjy.com )>5,即d>r,即可得出结论.【来源:21·世纪·教育·网】
【解答】解:如图所示:
在等腰三角形ABC中,作AD⊥BC于D,
则BD=CD= ( http: / / www.21cnjy.com )BC=2,
∴AD= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=4 ( http: / / www.21cnjy.com )>5,
即d>r,
∴该圆与底边的位置关系是相离;
故选:A.
( http: / / www.21cnjy.com )
7.(2017 茂县一模)已知⊙O的半径为3,圆心O到直线L的距离为2,则直线L与⊙O的位置关系是( )21·世纪*教育网
A.相交 B.相切 C.相离 D.不能确定
【分析】根据圆O的半径和,圆心O到直线L的距离的大小,相交:d<r;相切:d=r;相离:d>r;即可选出答案.21*cnjy*com
【解答】解:∵⊙O的半径为3,圆心O到直线L的距离为2,
∵3>2,即:d<r,
∴直线L与⊙O的位置关系是相交.
故选A.
8.(2017 莱芜)如图,A ( http: / / www.21cnjy.com )B是⊙O的直径,直线DA与⊙O相切于点A,DO交⊙O于点C,连接BC,若∠ABC=21°,则∠ADC的度数为( )
( http: / / www.21cnjy.com )
A.46° B.47° C.48° D.49°
【分析】根据等边对等角可得∠B=∠BC ( http: / / www.21cnjy.com )O,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AOD=∠B+∠BCO,根据切线的性质可得∠OAD=90°,然后根据直角三角形两锐角互余求解即可.
【解答】解:∵OB=OC,
∴∠B=∠BCO=21°,
∴∠AOD=∠B+∠BCO=21°+21°=42°,
∵AB是⊙O的直径,直线DA与⊙O相切与点A,
∴∠OAD=90°,
∴∠ADC=90°﹣∠AOD=90°﹣42°=48°.
故选C.
9.(2017 吉林)如图,直线l是⊙O的 ( http: / / www.21cnjy.com )切线,A为切点,B为直线l上一点,连接OB交⊙O于点C.若AB=12,OA=5,则BC的长为( )
( http: / / www.21cnjy.com )
A.5 B.6 C.7 D.8
【分析】根据勾股定理,可得OB的长,根据线段的和差,可得答案.
【解答】解:由勾股定理,得
OB= ( http: / / www.21cnjy.com )=13,
CB=OB﹣OC=13﹣5=8,
故选:D.
10.(2017 长春)如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
A.29° B.32° C.42° D.58°
【分析】作直径B′C,交⊙O ( http: / / www.21cnjy.com )于B′,连接AB′,则∠AB′C=∠ABC=29°,由等腰三角形的性质和三角形的外角的性质可求得∠DOC=54°,接下来,由切线的性质可证明∠OCD=90°,最后在Rt△OCD中根据两锐角互余可求得∠D的度数.
【解答】解:作直径B′C,交⊙O于B′,连接AB′,则∠AB′C=∠ABC=29°,
∵OA=OB′,
∴∠AB′C=∠OAB′=29°.
∴∠DOC=∠AB′C+∠OAB′=58°.
∵CD是⊙的切线,
∴∠OCD=90°.
∴∠D=90°﹣58°=32°.
故选B.
( http: / / www.21cnjy.com )
二.填空题(每小题5分,共30分)
11.(2017 江阴市二模)如图,在 ( http: / / www.21cnjy.com )Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上.则以MN为直径的圆与直线AB的位置关系是 相交 .
( http: / / www.21cnjy.com )
【分析】如图连接PC交MN于D,取MN ( http: / / www.21cnjy.com )的中点O,连接OP,由题意PD<OP,推出圆心O到直线AB的距离小于⊙O的半径,推出以MN为直径的圆与直线AB相交.www.21-cn-jy.com
【解答】解:如图连接PC交MN于D,取MN的中点O,连接OP,
( http: / / www.21cnjy.com )
由题意PD<OP,
∴圆心O到直线AB的距离小于⊙O的半径,
∴以MN为直径的圆与直线AB相交,
故答案为相交;
12.(2016秋 徐州期末)若⊙O的半径为4cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系是 相离 .
【分析】由题意得出d>r,根据直线和圆的位置关系的判定方法判断即可.
【解答】解:∴⊙O的半径为4cm,如果圆心O到直线l的距离为5cm,
∴5>4,
即d>r,
∴直线l与⊙O的位置关系是相离,
故答案为:相离.
13.(2016秋 东台市期末)已知点O ( http: / / www.21cnjy.com )到直线l的距离为6,以O为圆心,r为半径作⊙O,若⊙O上只有3个点到直线l的距离为2,则r的值为 8 .
【分析】根据点O到直线l的距离为6,要使⊙O上有且只有三个点到直线l的距离等于2,据此画出图形,此时圆的半径是6+2=8.21·cn·jy·com
【解答】解:由图可知,r=6+2=8,
( http: / / www.21cnjy.com )
故答案为:8.
14.(2017 黑龙江)如图,BD是⊙O的切线,B为切点,连接DO与⊙O交于点C,AB为⊙O的直径,连接CA,若∠D=30°,⊙O的半径为4,则图中阴影部分的面积为 ( http: / / www.21cnjy.com ) .【版权所有:21教育】
( http: / / www.21cnjy.com )
【分析】由条件可求得∠COA的度数,过O作OE⊥CA于点E,则可求得OE的长和CA的长,再利用S阴影=S扇形COA﹣S△COA可求得答案.
【解答】解:如图,过O作OE⊥CA于点E,
∵DB为⊙O的切线,
∴∠DBA=90°,
∵∠D=30°,
∴∠BOC=60°,
∴∠COA=120°,
∵OC=OA=4,
∴∠OAE=30°,
∴OE=2,CA=2AE=4 ( http: / / www.21cnjy.com )
∴S阴影=S扇形COA﹣S△COA= ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com )×2×4 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )π﹣4 ( http: / / www.21cnjy.com ),
故答案为: ( http: / / www.21cnjy.com )π﹣4 ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
15.(2017 衢州)如图,在直角坐标系中,⊙A的圆心A的坐标为(﹣1,0),半径为1,点P为直线y=﹣ ( http: / / www.21cnjy.com )x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是 2 ( http: / / www.21cnjy.com ) .
( http: / / www.21cnjy.com )
【分析】连接AP,PQ,当AP最小时,PQ最小,当AP⊥直线y=﹣ ( http: / / www.21cnjy.com )x+3时,PQ最小,根据全等三角形的性质得到AP=3,根据勾股定理即可得到结论.
【解答】解:如图,作AP⊥直线y=﹣ ( http: / / www.21cnjy.com )x+3,垂足为P,作⊙A的切线PQ,切点为Q,此时切线长PQ最小∵A的坐标为(﹣1,0),
设直线与x轴,y轴分别交于B,C,
∴B(0,3),C(4,0),
∴OB=3,AC=5,
∴BC= ( http: / / www.21cnjy.com )=5,
∴AC=BC,
在△APC与△BOC中, ( http: / / www.21cnjy.com ),
∴△APC≌△OBC,
∴AP=OB=3,
∴PQ= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
16.(2017 徐州)如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB= 60 °.21cnjy.com
( http: / / www.21cnjy.com )
【分析】由垂径定理易得BD=1,通过解直角三 ( http: / / www.21cnjy.com )角形ABD得到∠A=30°,然后由切线的性质和直角三角形的两个锐角互余的性质可以求得∠AOB的度数.
【解答】解:∵OA⊥BC,BC=2,
∴根据垂径定理得:BD= ( http: / / www.21cnjy.com )BC=1.
在Rt△ABD中,sin∠A= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
∴∠A=30°.
∵AB与⊙O相切于点B,
∴∠ABO=90°.
∴∠AOB=60°.
故答案是:60.
三.解答题(共20分)
17.(10分)(2017 贺州)如 ( http: / / www.21cnjy.com )图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.【出处:21教育名师】
(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径.
( http: / / www.21cnjy.com )
【分析】(1)连接OD,由切线的性质和已知条件可证得OD∥EF,则可证得结论;
(2)过D作DG⊥AE于点G,连接CD,则可证得△ADF≌△ADG、△CDF≌△BDG,则可求得AB的长,可求得圆的半径.
【解答】(1)证明:
如图1,连接OD,
( http: / / www.21cnjy.com )
∵EF是⊙O的切线,且点D在⊙O上,
∴OD⊥EF,
∵OA=OD,
∴∠DAB=∠ADO,
∵AD平分∠BAC,
∴∠DAB=∠DAC,
∴∠ADO=∠DAC,
∴AF∥OD,
∴AF⊥EF;
(2)解:
如图2,过D作DG⊥AE于点G,连接CD,
( http: / / www.21cnjy.com )
∵∠BAD=∠DAF,AF⊥EF,DG⊥AE,
∴BD=CD,DG=DF,
在Rt△ADF和Rt△ADG中
( http: / / www.21cnjy.com )
∴Rt△ADF≌Rt△ADG(HL),
同理可得Rt△CDF≌Rt△BDG,
∴BG=CF=2,AG=AF=AC+CF=6+2=8,
∴AB=AG+BG=8+2=10,
∴⊙O的半径OA= ( http: / / www.21cnjy.com )AB=5.
18.(10分)(2017 天津)已知 ( http: / / www.21cnjy.com )AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC时,求∠CDO的大小.
( http: / / www.21cnjy.com )
【分析】(1)根据切线的性质:圆的切线垂 ( http: / / www.21cnjy.com )直于经过切点的半径,得∠TAB=90°,根据三角形内角和得∠T的度数,由直径所对的圆周角是直角和同弧所对的圆周角相等得∠CDB的度数;21世纪教育网版权所有
(2)如图②,连接AD,根据等边对 ( http: / / www.21cnjy.com )等角得:∠BCE=∠BEC=65°,利用同圆的半径相等知:OA=OD,同理∠ODA=∠OAD=65°,由此可得结论.
【解答】解:(1)如图①,连接AC,
∵AT是⊙O切线,AB是⊙O的直径,
∴AT⊥AB,即∠TAB=90°,
∵∠ABT=50°,
∴∠T=90°﹣∠ABT=40°,
由AB是⊙O的直径,得∠ACB=90°,
∴∠CAB=90°﹣∠ABC=40°,
∴∠CDB=∠CAB=40°;
(2)如图②,连接AD,
在△BCE中,BE=BC,∠EBC=50°,
∴∠BCE=∠BEC=65°,
∴∠BAD=∠BCD=65°,
∵OA=OD,
∴∠ODA=∠OAD=65°,
∵∠ADC=∠ABC=50°,
∴∠CDO=∠ODA﹣∠ADC=65°﹣50°=15°.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
3.6 直线和圆的位置关系
第一课时检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
1.(2017 百色)以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )www-2-1-cnjy-com
A.0≤b<2 ( http: / / www.21cnjy.com ) B.﹣2 ( http: / / www.21cnjy.com )
C.﹣2 ( http: / / www.21cnjy.com )2 ( http: / / www.21cnjy.com ) D.﹣2 ( http: / / www.21cnjy.com )<b<2 ( http: / / www.21cnjy.com )
2.(2017秋 海安县校级期中)已知⊙O和直线L相交,圆心到直线L的距离为10cm,则⊙O的半径可能为( )2-1-c-n-j-y
A.10cm B.6cm C.12cm D.以上都不对
3.(2017 市北区二模)⊙O的半径r=5cm,直线l到圆心O的距离d=4,则直线l与圆的位置关系( )
A.相离 B.相切 C.相交 D.重合
4.(2017 余杭区一模)在平面直角坐 ( http: / / www.21cnjy.com )标系xOy中,经过点(sin45°,cos30°)的直线,与以原点为圆心,2为半径的圆的位置关系是( )
A.相交 B.相切 C.相离 D.以上三者都有可能
5.(2017 徐州一模)如图,平面上⊙O ( http: / / www.21cnjy.com )与四条直线L1、L2、L3、L4的位置关系.若⊙O的半径为2cm,且O点到其中一条直线的距离为2.2cm,则这条直线是( )
( http: / / www.21cnjy.com )
A.Ll B.L2 C.L3 D.L4
6.(2017 阳谷县一模)已知等腰三角形 ( http: / / www.21cnjy.com )的腰长为6cm,底边长为4cm,以等腰三角形的顶角的顶点为圆心5cm为半径画圆,那么该圆与底边的位置关系是( )
A.相离 B.相切 C.相交 D.不能确定
7.(2017 茂县一模)已知⊙O的半径为3,圆心O到直线L的距离为2,则直线L与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
8.(2017 莱芜)如图 ( http: / / www.21cnjy.com ),AB是⊙O的直径,直线DA与⊙O相切于点A,DO交⊙O于点C,连接BC,若∠ABC=21°,则∠ADC的度数为( )
( http: / / www.21cnjy.com )
A.46° B.47° C.48° D.49°
9.(2017 吉林)如图,直线l是⊙ ( http: / / www.21cnjy.com )O的切线,A为切点,B为直线l上一点,连接OB交⊙O于点C.若AB=12,OA=5,则BC的长为( )
( http: / / www.21cnjy.com )
A.5 B.6 C.7 D.8
10.(2017 长春)如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )
( http: / / www.21cnjy.com )
A.29° B.32° C.42° D.58°
二.填空题(每小题5分,共30分)
11.(2017 江阴市二模)如图 ( http: / / www.21cnjy.com ),在Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上.则以MN为直径的圆与直线AB的位置关系是 .
( http: / / www.21cnjy.com )
12.(2016秋 徐州期末)若⊙O的半径为4cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系是 .21*cnjy*com
13.(2016秋 东台市期末)已 ( http: / / www.21cnjy.com )知点O到直线l的距离为6,以O为圆心,r为半径作⊙O,若⊙O上只有3个点到直线l的距离为2,则r的值为 .
14.(2017 黑龙江)如图,BD是⊙O的 ( http: / / www.21cnjy.com )切线,B为切点,连接DO与⊙O交于点C,AB为⊙O的直径,连接CA,若∠D=30°,⊙O的半径为4,则图中阴影部分的面积为 .
( http: / / www.21cnjy.com )
15.(2017 衢州)如图,在直角坐标系中,⊙A的圆心A的坐标为(﹣1,0),半径为1,点P为直线y=﹣ ( http: / / www.21cnjy.com )x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是 .
( http: / / www.21cnjy.com )
16.(2017 徐州)如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB= °.
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(10分)(2017 ( http: / / www.21cnjy.com ) 贺州)如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径.
( http: / / www.21cnjy.com )
18.(10分)(201 ( http: / / www.21cnjy.com )7 天津)已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC时,求∠CDO的大小.
( http: / / www.21cnjy.com )
3.6 直线和圆的位置关系
第一课时检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017 百色)以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )
A.0≤b<2 ( http: / / www.21cnjy.com ) B.﹣2 ( http: / / www.21cnjy.com ) C.﹣2 ( http: / / www.21cnjy.com )2 ( http: / / www.21cnjy.com ) D.﹣2 ( http: / / www.21cnjy.com )<b<2 ( http: / / www.21cnjy.com )
【分析】求出直线y=﹣x+b与圆相切, ( http: / / www.21cnjy.com )且函数经过一、二、四象限,和当直线y=﹣x+b与圆相切,且函数经过二、三、四象限时b的值,则相交时b的值在相切时的两个b的值之间.
【解答】解:当直线y=﹣x+b与圆相切,且函数经过一、二、四象限时,如图.
在y=﹣x+b中,令x=0时,y=b,则与y轴的交点是(0,b),
当y=0时,x=b,则A的交点是(b,0),
则OA=OB,即△OAB是等腰直角三角形.
连接圆心O和切点C.则OC=2.
则OB= ( http: / / www.21cnjy.com )OC=2 ( http: / / www.21cnjy.com ).即b=2 ( http: / / www.21cnjy.com );
同理,当直线y=﹣x+b与圆相切,且函数经过二、三、四象限时,b=﹣2 ( http: / / www.21cnjy.com ).
则若直线y=﹣x+b与⊙O相交,则b的取值范围是﹣2 ( http: / / www.21cnjy.com )<b<2 ( http: / / www.21cnjy.com ).
故选D.
( http: / / www.21cnjy.com )
2.(2017秋 海安县校级期中)已知⊙O和直线L相交,圆心到直线L的距离为10cm,则⊙O的半径可能为( )2·1·c·n·j·y
A.10cm B.6cm C.12cm D.以上都不对
【分析】若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
【解答】解:∵⊙O和直线L相交,
∴d<r
∵d=10cm
∴r>10
∴只有选项C符合条件,
故选C.
3.(2017 市北区二模)⊙O的半径r=5cm,直线l到圆心O的距离d=4,则直线l与圆的位置关系( )21教育名师原创作品
A.相离 B.相切 C.相交 D.重合
【分析】由题意得出d<r,根据直线和圆的位置关系的判定方法判断即可.
【解答】解:∴⊙O的半径为5cm,如果圆心O到直线l的距离为4cm,
∴5>4,
即d<r,
∴直线l与⊙O的位置关系是相交,
故选C.
4.(2017 余杭区一模)在平面直角 ( http: / / www.21cnjy.com )坐标系xOy中,经过点(sin45°,cos30°)的直线,与以原点为圆心,2为半径的圆的位置关系是( )
A.相交 B.相切
C.相离 D.以上三者都有可能
【分析】设直线经过的点为A,若点A ( http: / / www.21cnjy.com )在圆内则直线和圆一定相交;若点在圆上或圆外则直线和圆有可能相交或相切或相离,所以先要计算OA的长和半径2比较大小再做选择.21教育网
【解答】解:设直线经过的点为A,
∵点A的坐标为(sin45°,cos30°),
∴OA= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∵圆的半径为2,
∴OA<2,
∴点A在圆内,
∴直线和圆一定相交,
故选A.
( http: / / www.21cnjy.com )
5.(2017 徐州一模)如图,平面上⊙ ( http: / / www.21cnjy.com )O与四条直线L1、L2、L3、L4的位置关系.若⊙O的半径为2cm,且O点到其中一条直线的距离为2.2cm,则这条直线是( )
( http: / / www.21cnjy.com )
A.Ll B.L2 C.L3 D.L4
【分析】根据直线和圆的位置关系与数量 ( http: / / www.21cnjy.com )之间的联系:当d=r,则直线和圆相切;当d<r,则直线和圆相交;当d>r,则直线和圆相离,进行分析判断.
【解答】解:因为所求直线到圆心O点的距离为2.2cm>半径2cm,
所以此直线与圆O相离,即为直线l3.
故选C.
6.(2017 阳谷县一模)已知等腰三 ( http: / / www.21cnjy.com )角形的腰长为6cm,底边长为4cm,以等腰三角形的顶角的顶点为圆心5cm为半径画圆,那么该圆与底边的位置关系是( )
A.相离 B.相切 C.相交 D.不能确定
【分析】作AD⊥BC于D,由等腰三角形的性质得出BD=CD= ( http: / / www.21cnjy.com )BC=2,由勾股定理求出AD=4 ( http: / / www.21cnjy.com )>5,即d>r,即可得出结论.【来源:21·世纪·教育·网】
【解答】解:如图所示:
在等腰三角形ABC中,作AD⊥BC于D,
则BD=CD= ( http: / / www.21cnjy.com )BC=2,
∴AD= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=4 ( http: / / www.21cnjy.com )>5,
即d>r,
∴该圆与底边的位置关系是相离;
故选:A.
( http: / / www.21cnjy.com )
7.(2017 茂县一模)已知⊙O的半径为3,圆心O到直线L的距离为2,则直线L与⊙O的位置关系是( )21·世纪*教育网
A.相交 B.相切 C.相离 D.不能确定
【分析】根据圆O的半径和,圆心O到直线L的距离的大小,相交:d<r;相切:d=r;相离:d>r;即可选出答案.21*cnjy*com
【解答】解:∵⊙O的半径为3,圆心O到直线L的距离为2,
∵3>2,即:d<r,
∴直线L与⊙O的位置关系是相交.
故选A.
8.(2017 莱芜)如图,A ( http: / / www.21cnjy.com )B是⊙O的直径,直线DA与⊙O相切于点A,DO交⊙O于点C,连接BC,若∠ABC=21°,则∠ADC的度数为( )
( http: / / www.21cnjy.com )
A.46° B.47° C.48° D.49°
【分析】根据等边对等角可得∠B=∠BC ( http: / / www.21cnjy.com )O,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AOD=∠B+∠BCO,根据切线的性质可得∠OAD=90°,然后根据直角三角形两锐角互余求解即可.
【解答】解:∵OB=OC,
∴∠B=∠BCO=21°,
∴∠AOD=∠B+∠BCO=21°+21°=42°,
∵AB是⊙O的直径,直线DA与⊙O相切与点A,
∴∠OAD=90°,
∴∠ADC=90°﹣∠AOD=90°﹣42°=48°.
故选C.
9.(2017 吉林)如图,直线l是⊙O的 ( http: / / www.21cnjy.com )切线,A为切点,B为直线l上一点,连接OB交⊙O于点C.若AB=12,OA=5,则BC的长为( )
( http: / / www.21cnjy.com )
A.5 B.6 C.7 D.8
【分析】根据勾股定理,可得OB的长,根据线段的和差,可得答案.
【解答】解:由勾股定理,得
OB= ( http: / / www.21cnjy.com )=13,
CB=OB﹣OC=13﹣5=8,
故选:D.
10.(2017 长春)如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
A.29° B.32° C.42° D.58°
【分析】作直径B′C,交⊙O ( http: / / www.21cnjy.com )于B′,连接AB′,则∠AB′C=∠ABC=29°,由等腰三角形的性质和三角形的外角的性质可求得∠DOC=54°,接下来,由切线的性质可证明∠OCD=90°,最后在Rt△OCD中根据两锐角互余可求得∠D的度数.
【解答】解:作直径B′C,交⊙O于B′,连接AB′,则∠AB′C=∠ABC=29°,
∵OA=OB′,
∴∠AB′C=∠OAB′=29°.
∴∠DOC=∠AB′C+∠OAB′=58°.
∵CD是⊙的切线,
∴∠OCD=90°.
∴∠D=90°﹣58°=32°.
故选B.
( http: / / www.21cnjy.com )
二.填空题(每小题5分,共30分)
11.(2017 江阴市二模)如图,在 ( http: / / www.21cnjy.com )Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上.则以MN为直径的圆与直线AB的位置关系是 相交 .
( http: / / www.21cnjy.com )
【分析】如图连接PC交MN于D,取MN ( http: / / www.21cnjy.com )的中点O,连接OP,由题意PD<OP,推出圆心O到直线AB的距离小于⊙O的半径,推出以MN为直径的圆与直线AB相交.www.21-cn-jy.com
【解答】解:如图连接PC交MN于D,取MN的中点O,连接OP,
( http: / / www.21cnjy.com )
由题意PD<OP,
∴圆心O到直线AB的距离小于⊙O的半径,
∴以MN为直径的圆与直线AB相交,
故答案为相交;
12.(2016秋 徐州期末)若⊙O的半径为4cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系是 相离 .
【分析】由题意得出d>r,根据直线和圆的位置关系的判定方法判断即可.
【解答】解:∴⊙O的半径为4cm,如果圆心O到直线l的距离为5cm,
∴5>4,
即d>r,
∴直线l与⊙O的位置关系是相离,
故答案为:相离.
13.(2016秋 东台市期末)已知点O ( http: / / www.21cnjy.com )到直线l的距离为6,以O为圆心,r为半径作⊙O,若⊙O上只有3个点到直线l的距离为2,则r的值为 8 .
【分析】根据点O到直线l的距离为6,要使⊙O上有且只有三个点到直线l的距离等于2,据此画出图形,此时圆的半径是6+2=8.21·cn·jy·com
【解答】解:由图可知,r=6+2=8,
( http: / / www.21cnjy.com )
故答案为:8.
14.(2017 黑龙江)如图,BD是⊙O的切线,B为切点,连接DO与⊙O交于点C,AB为⊙O的直径,连接CA,若∠D=30°,⊙O的半径为4,则图中阴影部分的面积为 ( http: / / www.21cnjy.com ) .【版权所有:21教育】
( http: / / www.21cnjy.com )
【分析】由条件可求得∠COA的度数,过O作OE⊥CA于点E,则可求得OE的长和CA的长,再利用S阴影=S扇形COA﹣S△COA可求得答案.
【解答】解:如图,过O作OE⊥CA于点E,
∵DB为⊙O的切线,
∴∠DBA=90°,
∵∠D=30°,
∴∠BOC=60°,
∴∠COA=120°,
∵OC=OA=4,
∴∠OAE=30°,
∴OE=2,CA=2AE=4 ( http: / / www.21cnjy.com )
∴S阴影=S扇形COA﹣S△COA= ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com )×2×4 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )π﹣4 ( http: / / www.21cnjy.com ),
故答案为: ( http: / / www.21cnjy.com )π﹣4 ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
15.(2017 衢州)如图,在直角坐标系中,⊙A的圆心A的坐标为(﹣1,0),半径为1,点P为直线y=﹣ ( http: / / www.21cnjy.com )x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是 2 ( http: / / www.21cnjy.com ) .
( http: / / www.21cnjy.com )
【分析】连接AP,PQ,当AP最小时,PQ最小,当AP⊥直线y=﹣ ( http: / / www.21cnjy.com )x+3时,PQ最小,根据全等三角形的性质得到AP=3,根据勾股定理即可得到结论.
【解答】解:如图,作AP⊥直线y=﹣ ( http: / / www.21cnjy.com )x+3,垂足为P,作⊙A的切线PQ,切点为Q,此时切线长PQ最小∵A的坐标为(﹣1,0),
设直线与x轴,y轴分别交于B,C,
∴B(0,3),C(4,0),
∴OB=3,AC=5,
∴BC= ( http: / / www.21cnjy.com )=5,
∴AC=BC,
在△APC与△BOC中, ( http: / / www.21cnjy.com ),
∴△APC≌△OBC,
∴AP=OB=3,
∴PQ= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
16.(2017 徐州)如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB= 60 °.21cnjy.com
( http: / / www.21cnjy.com )
【分析】由垂径定理易得BD=1,通过解直角三 ( http: / / www.21cnjy.com )角形ABD得到∠A=30°,然后由切线的性质和直角三角形的两个锐角互余的性质可以求得∠AOB的度数.
【解答】解:∵OA⊥BC,BC=2,
∴根据垂径定理得:BD= ( http: / / www.21cnjy.com )BC=1.
在Rt△ABD中,sin∠A= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
∴∠A=30°.
∵AB与⊙O相切于点B,
∴∠ABO=90°.
∴∠AOB=60°.
故答案是:60.
三.解答题(共20分)
17.(10分)(2017 贺州)如 ( http: / / www.21cnjy.com )图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.【出处:21教育名师】
(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径.
( http: / / www.21cnjy.com )
【分析】(1)连接OD,由切线的性质和已知条件可证得OD∥EF,则可证得结论;
(2)过D作DG⊥AE于点G,连接CD,则可证得△ADF≌△ADG、△CDF≌△BDG,则可求得AB的长,可求得圆的半径.
【解答】(1)证明:
如图1,连接OD,
( http: / / www.21cnjy.com )
∵EF是⊙O的切线,且点D在⊙O上,
∴OD⊥EF,
∵OA=OD,
∴∠DAB=∠ADO,
∵AD平分∠BAC,
∴∠DAB=∠DAC,
∴∠ADO=∠DAC,
∴AF∥OD,
∴AF⊥EF;
(2)解:
如图2,过D作DG⊥AE于点G,连接CD,
( http: / / www.21cnjy.com )
∵∠BAD=∠DAF,AF⊥EF,DG⊥AE,
∴BD=CD,DG=DF,
在Rt△ADF和Rt△ADG中
( http: / / www.21cnjy.com )
∴Rt△ADF≌Rt△ADG(HL),
同理可得Rt△CDF≌Rt△BDG,
∴BG=CF=2,AG=AF=AC+CF=6+2=8,
∴AB=AG+BG=8+2=10,
∴⊙O的半径OA= ( http: / / www.21cnjy.com )AB=5.
18.(10分)(2017 天津)已知 ( http: / / www.21cnjy.com )AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC时,求∠CDO的大小.
( http: / / www.21cnjy.com )
【分析】(1)根据切线的性质:圆的切线垂 ( http: / / www.21cnjy.com )直于经过切点的半径,得∠TAB=90°,根据三角形内角和得∠T的度数,由直径所对的圆周角是直角和同弧所对的圆周角相等得∠CDB的度数;21世纪教育网版权所有
(2)如图②,连接AD,根据等边对 ( http: / / www.21cnjy.com )等角得:∠BCE=∠BEC=65°,利用同圆的半径相等知:OA=OD,同理∠ODA=∠OAD=65°,由此可得结论.
【解答】解:(1)如图①,连接AC,
∵AT是⊙O切线,AB是⊙O的直径,
∴AT⊥AB,即∠TAB=90°,
∵∠ABT=50°,
∴∠T=90°﹣∠ABT=40°,
由AB是⊙O的直径,得∠ACB=90°,
∴∠CAB=90°﹣∠ABC=40°,
∴∠CDB=∠CAB=40°;
(2)如图②,连接AD,
在△BCE中,BE=BC,∠EBC=50°,
∴∠BCE=∠BEC=65°,
∴∠BAD=∠BCD=65°,
∵OA=OD,
∴∠ODA=∠OAD=65°,
∵∠ADC=∠ABC=50°,
∴∠CDO=∠ODA﹣∠ADC=65°﹣50°=15°.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
