3.8 圆内接正多边形一课一测
图片预览

文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
3.8 圆内接正多边形检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
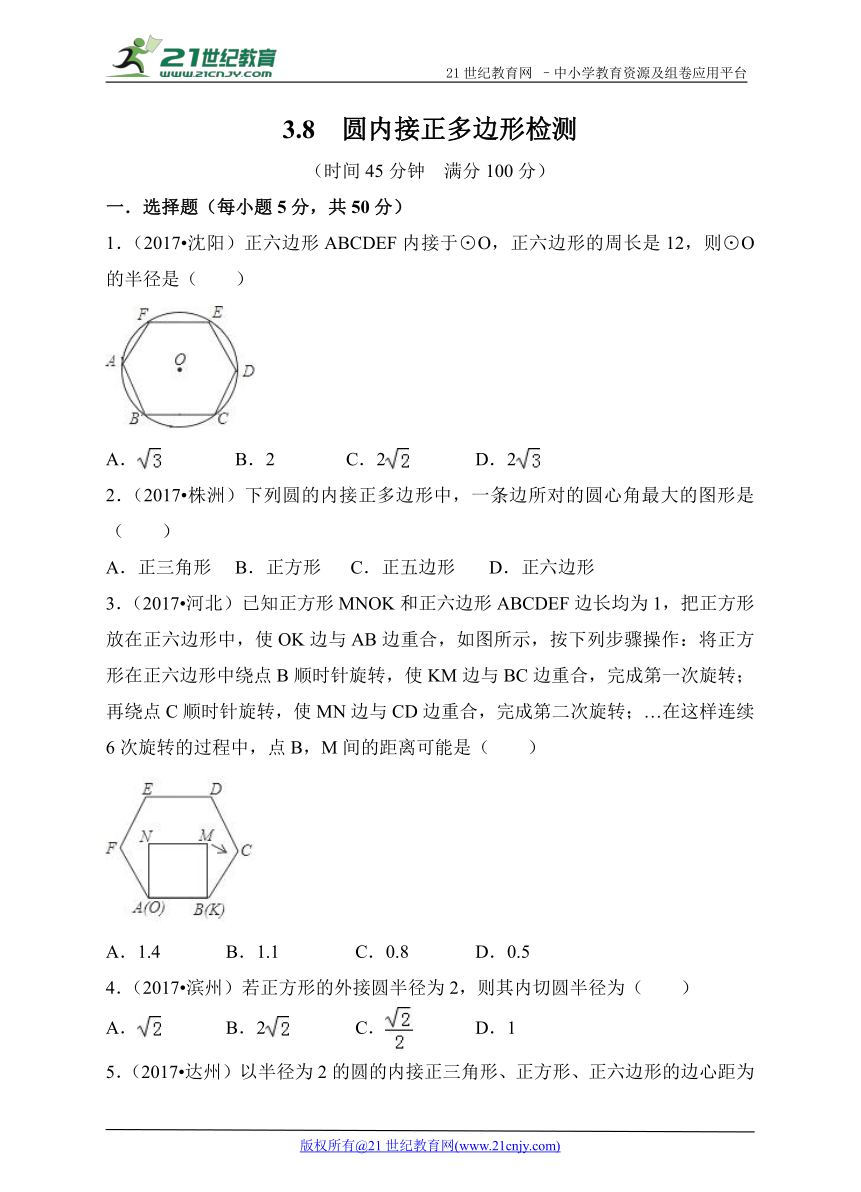
1.(2017 沈阳)正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.2 C.2 ( http: / / www.21cnjy.com ) D.2 ( http: / / www.21cnjy.com )
2.(2017 株洲)下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
3.(2017 河北)已知正方形MNOK ( http: / / www.21cnjy.com )和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使K ( http: / / www.21cnjy.com )M边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
( http: / / www.21cnjy.com )
A.1.4 B.1.1 C.0.8 D.0.5
4.(2017 滨州)若正方形的外接圆半径为2,则其内切圆半径为( )
A. ( http: / / www.21cnjy.com ) B.2 ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.1
5.(2017 达州)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )21*cnjy*com
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
6.(2017 日照)下列说法正确的是( )
A.圆内接正六边形的边长与该圆的半径相等
B.在平面直角坐标系中,不同的坐标可以表示同一点
C.一元二次方程ax2+bx+c=0(a≠0)一定有实数根
D.将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等
7.(2017 兰州)如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A.π+1 B.π+2 C.π﹣1 D.π﹣2
8.(2017 莱芜)如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣ ( http: / / www.21cnjy.com );③(S四边形CDEF)2=9+2 ( http: / / www.21cnjy.com );④DF2﹣DG2=7﹣2 ( http: / / www.21cnjy.com ).其中结论正确的个数是( )
( http: / / www.21cnjy.com )
A.1 B.2 C.3 D.4
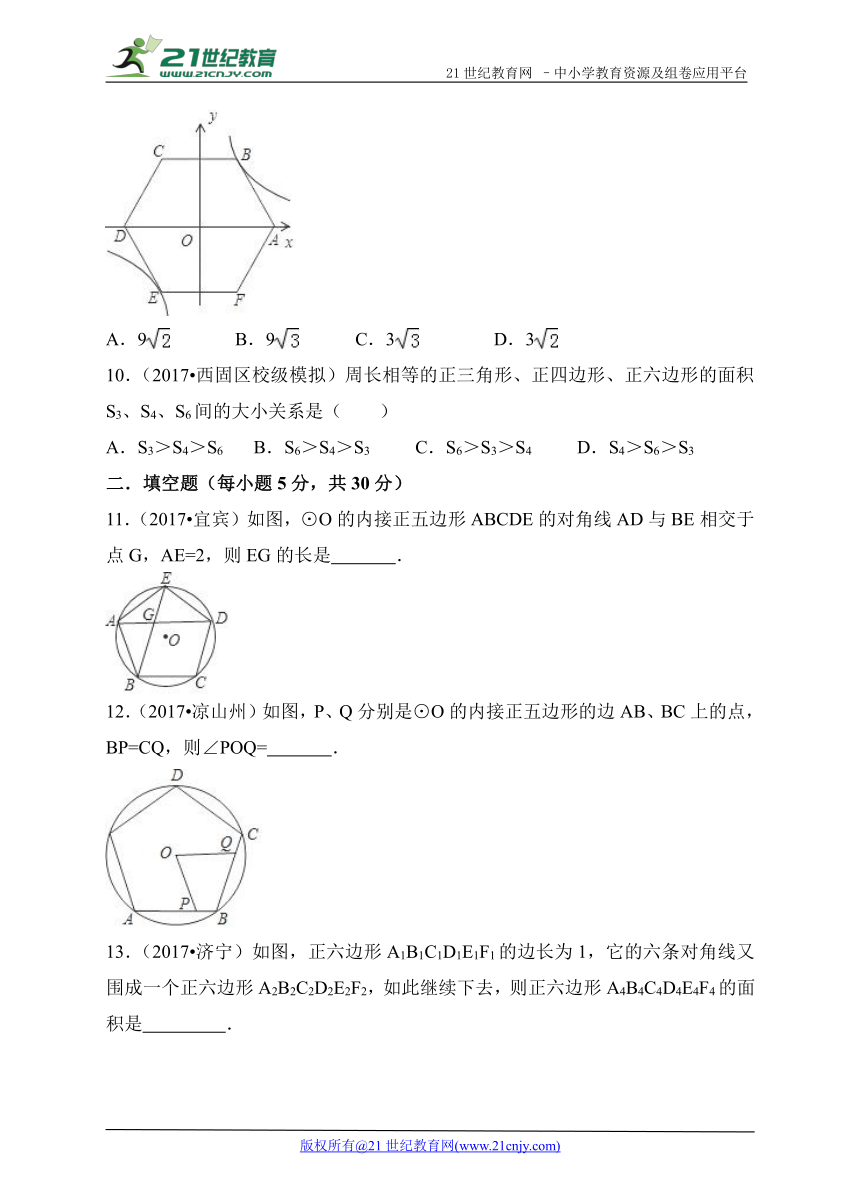
9.(2017 石家庄模拟)如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y= ( http: / / www.21cnjy.com )位于第一象限的图象上,则k的值为( )21教育网
( http: / / www.21cnjy.com )
A.9 ( http: / / www.21cnjy.com ) B.9 ( http: / / www.21cnjy.com ) C.3 ( http: / / www.21cnjy.com ) D.3 ( http: / / www.21cnjy.com )
10.(2017 西固区校级模拟)周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是( )
A.S3>S4>S6 B.S6>S4>S3 C.S6>S3>S4 D.S4>S6>S3
二.填空题(每小题5分,共30分)
11.(2017 宜宾)如图,⊙O的内接正五边形ABCDE的对角线AD与BE相交于点G,AE=2,则EG的长是 .
( http: / / www.21cnjy.com )
12.(2017 凉山州)如图,P、Q分别是⊙O的内接正五边形的边AB、BC上的点,BP=CQ,则∠POQ= .
( http: / / www.21cnjy.com )
13.(2017 济宁)如图,正六边形A1 ( http: / / www.21cnjy.com )B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是 .
( http: / / www.21cnjy.com )
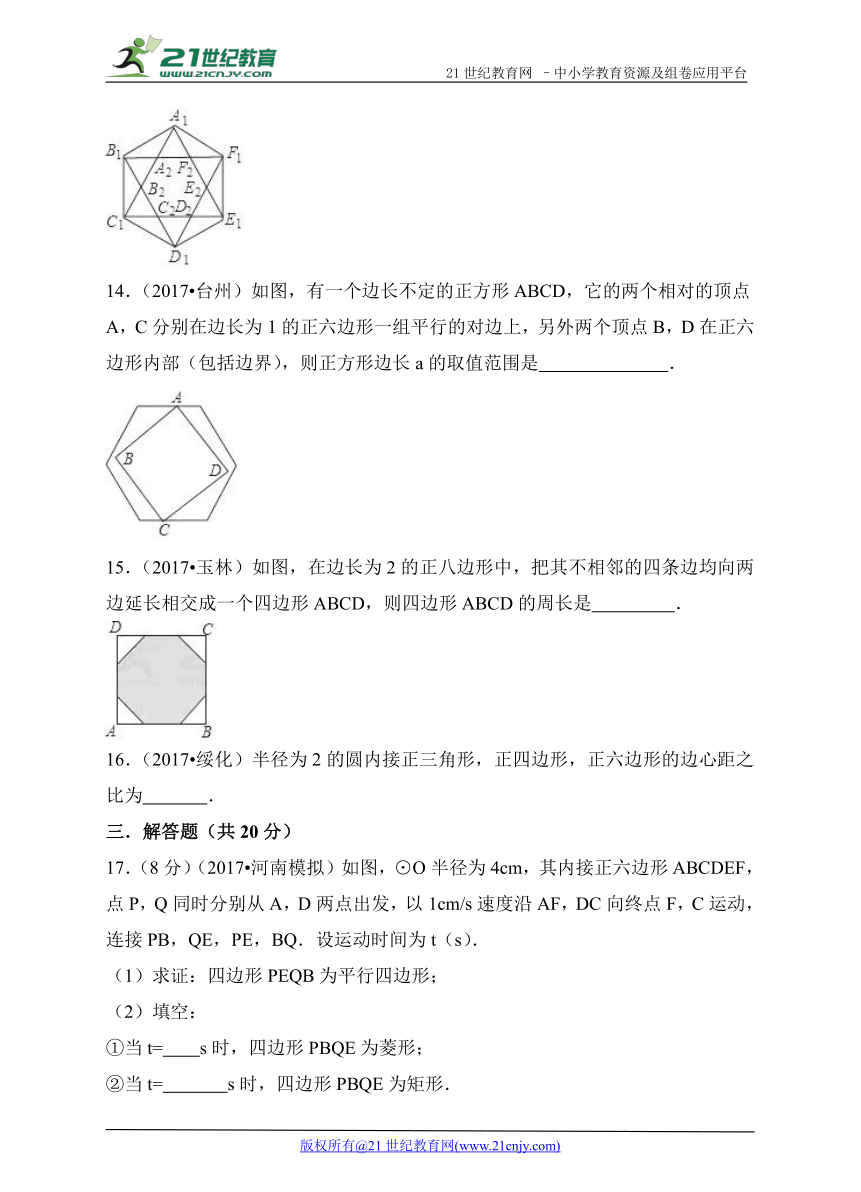
14.(2017 台州)如 ( http: / / www.21cnjy.com )图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是 .
( http: / / www.21cnjy.com )
15.(2017 玉林)如图,在边长为 ( http: / / www.21cnjy.com )2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是 .
( http: / / www.21cnjy.com )
16.(2017 绥化)半径为2的圆内接正三角形,正四边形,正六边形的边心距之比为 .
三.解答题(共20分)
17.(8分)(2017 河南模拟 ( http: / / www.21cnjy.com ))如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s).
(1)求证:四边形PEQB为平行四边形;
(2)填空:
①当t= s时,四边形PBQE为菱形;
②当t= s时,四边形PBQE为矩形.
( http: / / www.21cnjy.com )
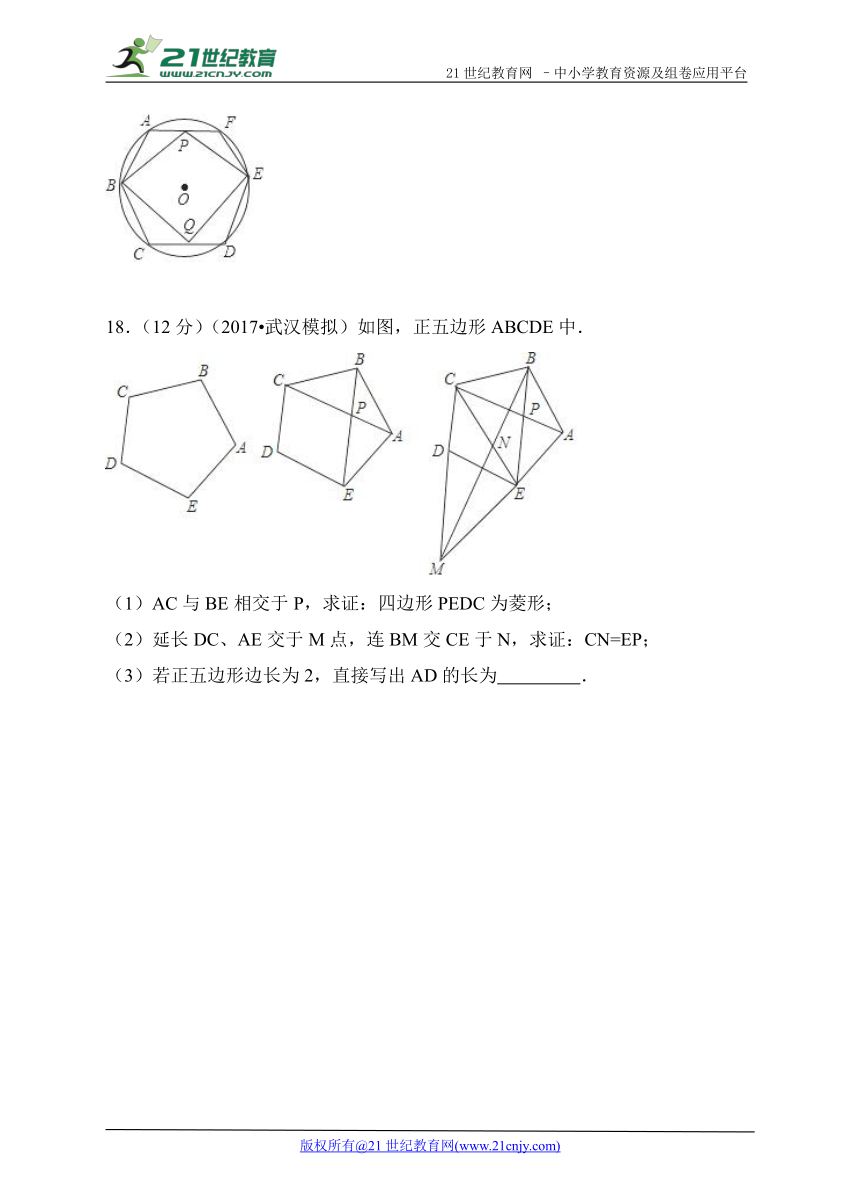
18.(12分)(2017 武汉模拟)如图,正五边形ABCDE中.
( http: / / www.21cnjy.com )
(1)AC与BE相交于P,求证:四边形PEDC为菱形;
(2)延长DC、AE交于M点,连BM交CE于N,求证:CN=EP;
(3)若正五边形边长为2,直接写出AD的长为 .
3.8 圆内接正多边形检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017 沈阳)正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.2 C.2 ( http: / / www.21cnjy.com ) D.2 ( http: / / www.21cnjy.com )
【分析】连接OA,OB,根据等边三角形的性质可得⊙O的半径,进而可得出结论.
【解答】解:连接OB,OC,
∵多边形ABCDEF是正六边形,
∴∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴OB=BC,
∵正六边形的周长是12,
∴BC=2,
∴⊙O的半径是2,
故选B.
( http: / / www.21cnjy.com )
2.(2017 株洲)下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
【分析】根据正多边形的中心角的度数即可得到结论.
【解答】解:∵正三角形一条边所对的圆心角是360°÷3=120°,
正方形一条边所对的圆心角是360°÷4=90°,
正五边形一条边所对的圆心角是360°÷5=72°,
正六边形一条边所对的圆心角是360°÷6=60°,
∴一条边所对的圆心角最大的图形是正三角形,
故选A.
3.(2017 河北)已知正方形M ( http: / / www.21cnjy.com )NOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:
将正方形在正六边形中绕点B顺时针旋转,使KM ( http: / / www.21cnjy.com )边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
( http: / / www.21cnjy.com )
A.1.4 B.1.1 C.0.8 D.0.5
【分析】如图,在这样连续6次旋转的过程中,点M的运动轨迹是图中的红线,观察图象可知点B,M间的距离大于等于2﹣ ( http: / / www.21cnjy.com )小于等于1,由此即可判断.
【解答】解:如图,在这样连续6次旋转的过程中,点M的运动轨迹是图中的红线,
观察图象可知点B,M间的距离大于等于2﹣ ( http: / / www.21cnjy.com )小于等于1,
故选C.
( http: / / www.21cnjy.com )
4.(2017 滨州)若正方形的外接圆半径为2,则其内切圆半径为( )
A. ( http: / / www.21cnjy.com ) B.2 ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.1
【分析】根据题意画出图形,再由正方形及等腰直角三角形的性质求解即可.
【解答】解:如图所示,连接OA、OE,
∵AB是小圆的切线,
∴OE⊥AB,
∵四边形ABCD是正方形,
∴AE=OE,
∴△AOE是等腰直角三角形,
∴OE= ( http: / / www.21cnjy.com )OA= ( http: / / www.21cnjy.com ).
故选A.
( http: / / www.21cnjy.com )
5.(2017 达州)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】由于内接正三角形、 ( http: / / www.21cnjy.com )正方形、正六边形是特殊内角的多边形,可构造直角三角形分别求出边心距的长,由勾股定理逆定理可得该三角形是直角三角形,进而可得其面积.
【解答】解:如图1,
( http: / / www.21cnjy.com )
∵OC=2,
∴OD=2×sin30°=1;
如图2,
( http: / / www.21cnjy.com )
∵OB=2,
∴OE=2×sin45°= ( http: / / www.21cnjy.com );
如图3,
( http: / / www.21cnjy.com )
∵OA=2,
∴OD=2×cos30°= ( http: / / www.21cnjy.com ),
则该三角形的三边分别为:1, ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),
∵(1)2+( ( http: / / www.21cnjy.com ))2=( ( http: / / www.21cnjy.com ))2,
∴该三角形是直角三角形,
∴该三角形的面积是: ( http: / / www.21cnjy.com )×1× ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
故选:A.
6.(2017 日照)下列说法正确的是( )
A.圆内接正六边形的边长与该圆的半径相等
B.在平面直角坐标系中,不同的坐标可以表示同一点
C.一元二次方程ax2+bx+c=0(a≠0)一定有实数根
D.将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等
【分析】根据正多边形和圆的关系、一元二次方程根的判别式、点的坐标以及旋转变换的性质进行判断即可.
【解答】解:如图∠AOB= ( http: / / www.21cnjy.com )=60°,OA=OB,
∴△AOB是等边三角形,
∴AB=OA,
∴圆内接正六边形的边长与该圆的半径相等,A正确;
在平面直角坐标系中,不同的坐标可以表示不同一点,B错误;
一元二次方程ax2+bx+c=0(a≠0)不一定有实数根,C错误;
根据旋转变换的性质可知,将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE全等,D错误;2-1-c-n-j-y
故选:A.
( http: / / www.21cnjy.com )
7.(2017 兰州)如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A.π+1 B.π+2 C.π﹣1 D.π﹣2
【分析】根据对称性可知阴影部分的面积等于圆的面积减去正方形的 ( http: / / www.21cnjy.com ),求出圆内接正方形的边长,即可求解.
【解答】解:连接AO,DO,
∵ABCD是正方形,
∴∠AOD=90°,
AD= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com ),
圆内接正方形的边长为2 ( http: / / www.21cnjy.com ),所以阴影部分的面积= ( http: / / www.21cnjy.com )[4π﹣(2 ( http: / / www.21cnjy.com ))2]=(π﹣2)cm2.
故选D.
( http: / / www.21cnjy.com )
8.(2017 莱芜)如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣ ( http: / / www.21cnjy.com );③(S四边形CDEF)2=9+2 ( http: / / www.21cnjy.com );④DF2﹣DG2=7﹣2 ( http: / / www.21cnjy.com ).其中结论正确的个数是( )【版权所有:21教育】
( http: / / www.21cnjy.com )
A.1 B.2 C.3 D.4
【分析】①先根据正五方形ABCDE的性质得:∠ABC=180°﹣ ( http: / / www.21cnjy.com )=108°,由等边对等角可得:∠BAC=∠ACB=36°,再利用角相等求BC=CF=CD,得∠CDF=∠CFD= ( http: / / www.21cnjy.com )=54°,可得∠FDG=18°;
②证明△ABF∽△ACB,得 ( http: / / www.21cnjy.com ),代入可得FG的长;
③如图1,先证明四边形CDEF是平行四边形,根据平行四边形的面积公式可得:(S四边形CDEF)2=EF2 DM2=4× ( http: / / www.21cnjy.com )=10+2 ( http: / / www.21cnjy.com );
④如图2, CDEF是菱形,先计算EC=BE=4﹣FG=1+ ( http: / / www.21cnjy.com ),由S四边形CDEF= ( http: / / www.21cnjy.com )FD EC=2× ( http: / / www.21cnjy.com ),可得FD2=10﹣2 ( http: / / www.21cnjy.com ),计算可得结论.
【解答】解:①∵五方形ABCDE是正五边形,
∴AB=BC,∠ABC=180°﹣ ( http: / / www.21cnjy.com )=108°,
∴∠BAC=∠ACB=36°,
∴∠ACD=108°﹣36°=72°,
同理得:∠ADE=36°,
∵∠BAE=108°,AB=AE,
∴∠ABE=36°,
∴∠CBF=108°﹣36°=72°,
∴BC=FC,
∵BC=CD,
∴CD=CF,
∴∠CDF=∠CFD= ( http: / / www.21cnjy.com )=54°,
∴∠FDG=∠CDE﹣∠CDF﹣∠ADE=108°﹣54°﹣36°=18°;
所以①正确;
②∵∠ABE=∠ACB=36°,∠BAC=∠BAF,
∴△ABF∽△ACB,
∴ ( http: / / www.21cnjy.com ),
∴AB ED=AC EG,
∵AB=ED=2,AC=BE=BG+EF﹣FG=2AB﹣FG=4﹣FG,EG=BG﹣FG=2﹣FG,
∴22=(2﹣FG)(4﹣FG),
∴FG=3+ ( http: / / www.21cnjy.com )>2(舍),FG=3﹣ ( http: / / www.21cnjy.com );
所以②正确;
③如图1,∵∠EBC=72°,∠BCD=108°,
∴∠EBC+∠BCD=180°,
∴EF∥CD,
∵EF=CD=2,
∴四边形CDEF是平行四边形,
过D作DM⊥EG于M,
∵DG=DE,
∴EM=MG= ( http: / / www.21cnjy.com )EG= ( http: / / www.21cnjy.com )(EF﹣FG)= ( http: / / www.21cnjy.com )(2﹣3+ ( http: / / www.21cnjy.com ))= ( http: / / www.21cnjy.com ),
由勾股定理得:DM= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴(S四边形CDEF)2=EF2 DM2=4× ( http: / / www.21cnjy.com )=10+2 ( http: / / www.21cnjy.com );
所以③不正确;
④如图2,连接EC,
∵EF=ED,
∴ CDEF是菱形,
∴FD⊥EC,
∵EC=BE=4﹣FG=4﹣(3﹣ ( http: / / www.21cnjy.com ))=1+ ( http: / / www.21cnjy.com ),
∴S四边形CDEF= ( http: / / www.21cnjy.com )FD EC=2× ( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com )×FD×(1+ ( http: / / www.21cnjy.com ))= ( http: / / www.21cnjy.com ),
FD2=10﹣2 ( http: / / www.21cnjy.com ),
∴DF2﹣DG2=10﹣2 ( http: / / www.21cnjy.com )﹣4=6﹣2 ( http: / / www.21cnjy.com ),
所以④不正确;
本题正确的有两个,
故选B.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
9.(2017 石家庄模拟)如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y= ( http: / / www.21cnjy.com )位于第一象限的图象上,则k的值为( )21世纪教育网版权所有
( http: / / www.21cnjy.com )
A.9 ( http: / / www.21cnjy.com ) B.9 ( http: / / www.21cnjy.com ) C.3 ( http: / / www.21cnjy.com ) D.3 ( http: / / www.21cnjy.com )
【分析】连接OB,过B作BG⊥OA于G,得出等边三角形OBA,求出OB,求出OG、BG,得出B的坐标,即可去除答案.21cnjy.com
【解答】解: ( http: / / www.21cnjy.com )
连接OB,过B作BG⊥OA于G,
∵ABCDEF是正六边形,
∴∠AOB=60°,
∵OB=OA,
∴△AOB是等边三角形,
∴OB=OA=AB=6,
∵BG⊥OA,
∴∠BGO=90°,
∴∠OBG=30°,
∴OG= ( http: / / www.21cnjy.com )OB=3,由勾股定理得:BG=3 ( http: / / www.21cnjy.com ),
即B的坐标是(3,3 ( http: / / www.21cnjy.com )),
∵B点在反比例函数y= ( http: / / www.21cnjy.com )上,
∴k=3×3 ( http: / / www.21cnjy.com )=9 ( http: / / www.21cnjy.com ),
故选B.
10.(2017 西固区校级模拟)周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是( )www.21-cn-jy.com
A.S3>S4>S6 B.S6>S4>S3 C.S6>S3>S4 D.S4>S6>S3
【分析】先根据题意画出图形设出正六边形的边长,再根据正三角形、正方形、正六边形的周长都相等求出各图形的边长,再分别求出其面积即可.
【解答】解:设正六边形的边长为a,如图所示,
则正△ABC的边长为2a,正方形ABCD的边长为 ( http: / / www.21cnjy.com ).
如图(1),过A作AD⊥BC,D为垂足;
∵△ABC是等边三角形,BC=2a,
∴BD=a,由勾股定理得,AD= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )a,
∴S3=S△ABC= ( http: / / www.21cnjy.com )BC AD= ( http: / / www.21cnjy.com )×2a× ( http: / / www.21cnjy.com )a= ( http: / / www.21cnjy.com )a2≈1.73a2.
如图(2),∵四边形ABCD是正方形,
∴AB= ( http: / / www.21cnjy.com ),
∴S4=S□ABCD=AB2= ( http: / / www.21cnjy.com )× ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )a2≈2.25a2.
如图(3),过O作OG⊥BC,G为垂足,
∵六边形ABCDEF是正六边形,
∴∠BOC= ( http: / / www.21cnjy.com )=60°,
∴∠BOG=30°,OG= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )a.
∴S△BOC= ( http: / / www.21cnjy.com )× ( http: / / www.21cnjy.com )a×a= ( http: / / www.21cnjy.com )a2,
∴S6=6S△BOC=6× ( http: / / www.21cnjy.com )a= ( http: / / www.21cnjy.com )a2≈2.59a2.
∵2.59a2>2.25a2>1.73a2.
∴S6>S4>S3.
故选:B.
( http: / / www.21cnjy.com )
二.填空题(每小题5分,共30分)
11.(2017 宜宾)如图,⊙O的内接正五边形ABCDE的对角线AD与BE相交于点G,AE=2,则EG的长是 ( http: / / www.21cnjy.com )﹣1 .21·世纪*教育网
( http: / / www.21cnjy.com )
【分析】在⊙O的内接正五 ( http: / / www.21cnjy.com )边形ABCDE中,设EG=x,易知:∠AEB=∠ABE=∠EAG=36°,∠BAG=∠AGB=72°,推出AB=BG=AE=2,由△AEG∽△BEA,可得AE2=EG EB,可得22=x(x+2),解方程即可.www-2-1-cnjy-com
【解答】解:在⊙O的内接正五边形ABCDE中,设EG=x,
易知:∠AEB=∠ABE=∠EAG=36°,
∠BAG=∠AGB=72°,
∴AB=BG=AE=2,
∵∠AEG=∠AEB,∠EAG=∠EBA,
∴△AEG∽△BEA,
∴AE2=EG EB,
∴22=x(x+2),
解得x=﹣1+ ( http: / / www.21cnjy.com )或﹣1﹣ ( http: / / www.21cnjy.com ),
∴EG= ( http: / / www.21cnjy.com )﹣1,
故答案为 ( http: / / www.21cnjy.com )﹣1.
12.(2017 凉山州)如图,P、Q分别是⊙O的内接正五边形的边AB、BC上的点,BP=CQ,则∠POQ= 72° .【出处:21教育名师】
( http: / / www.21cnjy.com )
【分析】连接OA、OB、OC,证明△OBP≌△OCQ,根据全等三角形的性质得到∠BOP=∠COQ,结合图形计算即可.21教育名师原创作品
【解答】解:连接OA、OB、OC,
∵五边形ABCDE是⊙O的内接正五边形,
∴∠AOB=∠BOC=72°,
∵OA=OB,OB=OC,
∴∠OBA=∠OCB=54°,
在△OBP和△OCQ中,
( http: / / www.21cnjy.com ),
∴△OBP≌△OCQ,
∴∠BOP=∠COQ,
∵∠AOB=∠AOP+∠BOP,∠BOC=∠BOQ+∠QOC,
∴∠BOP=∠QOC,
∵∠POQ=∠BOP+∠BOQ,∠BOC=∠BOQ+∠QOC,
∴∠POQ=∠BOC=72°.
故答案为:72°.
( http: / / www.21cnjy.com )
13.(2017 济宁)如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是 ( http: / / www.21cnjy.com ) .21*cnjy*com
( http: / / www.21cnjy.com )
【分析】由正六边形的性质得:∠A1B1B2=90°,∠B1A1B2=30°,A1A2=A2B2,由直角三角形的性质得出B1B2= ( http: / / www.21cnjy.com )A1B1= ( http: / / www.21cnjy.com ),A2B2= ( http: / / www.21cnjy.com )A1B2=B1B2= ( http: / / www.21cnjy.com ),由相似多边形的性质得出正六边形A2B2C2D2E2F2的面积:正六边形A1B1C1D1E1F1的面积= ( http: / / www.21cnjy.com ),求出正六边形A1B1C1D1E1F1的面积= ( http: / / www.21cnjy.com ),得出正六边形A2B2C2D2E2F2的面积,同理得出正六边形A4B4C4D4E4F4的面积.
【解答】解:由正六边形的性质得:∠A1B1B2=90°,∠B1A1B2=30°,A1A2=A2B2,
∴B1B2= ( http: / / www.21cnjy.com )A1B1= ( http: / / www.21cnjy.com ),
∴A2B2= ( http: / / www.21cnjy.com )A1B2=B1B2= ( http: / / www.21cnjy.com ),
∵正六边形A1B1C1D1E1F1∽正六边形A2B2C2D2E2F2,
∴正六边形A2B2C2D2E2F2的面积:正六边形A1B1C1D1E1F1的面积=( ( http: / / www.21cnjy.com ))2= ( http: / / www.21cnjy.com ),
∵正六边形A1B1C1D1E1F1的面积=6× ( http: / / www.21cnjy.com )×1× ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴正六边形A2B2C2D2E2F2的面积= ( http: / / www.21cnjy.com )× ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
同理:正六边形A4B4C4D4E4F4的面积=( ( http: / / www.21cnjy.com ))3× ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com );
故答案为: ( http: / / www.21cnjy.com ).
14.(2017 台州)如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是 ( http: / / www.21cnjy.com )≤a≤3﹣ ( http: / / www.21cnjy.com ) .
( http: / / www.21cnjy.com )
【分析】当正方形ABCD的顶点A、B、 ( http: / / www.21cnjy.com )C、D在正六边形的边上时,正方形的边长的值最大,解直角三角形得到a,当正方形ABCD的对角线AC在正六边形一组平行的对边的中点上时,正方形边长a的值最小,AC是正方形的对角线,解直角三角形即可得到结论.【来源:21cnj*y.co*m】
【解答】解:①当正方形ABCD的对角线AC在正六边形一组平行的对边的中点上时,
正方形边长a的值最小,AC是正方形的对角线,
∴AC=A′D= ( http: / / www.21cnjy.com ),
∴a= ( http: / / www.21cnjy.com ),
②当正方形ABCD的四个顶点都在正六边形的边上时,正方形边长a的值最大,AC是正方形的对角线AC,
设A′(t, ( http: / / www.21cnjy.com ))时,正方形的边长最大,
∵OB′⊥OA′,
∴B′(﹣ ( http: / / www.21cnjy.com ),t),
设直线MN的解析式为y=kx+b,M(﹣1,0),N(﹣ ( http: / / www.21cnjy.com ),﹣ ( http: / / www.21cnjy.com )),
∴ ( http: / / www.21cnjy.com ),
∴ ( http: / / www.21cnjy.com ),
∴直线MN的解析式为y=﹣ ( http: / / www.21cnjy.com )x﹣ ( http: / / www.21cnjy.com ),
将B′(﹣ ( http: / / www.21cnjy.com ),t)代入得t= ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com ),
此时,A′B′取最大值,
∴a= ( http: / / www.21cnjy.com )=3﹣ ( http: / / www.21cnjy.com ),
∴正方形边长a的取值范围是: ( http: / / www.21cnjy.com )≤a≤3﹣ ( http: / / www.21cnjy.com ),
故答案为: ( http: / / www.21cnjy.com )≤a≤3﹣ ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
15.(2017 玉林)如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是 8+8 ( http: / / www.21cnjy.com ) .
( http: / / www.21cnjy.com )
【分析】根据题意可知形成的四个小的直角 ( http: / / www.21cnjy.com )三角形全等,并且四个都是等腰直角三角形,从而可以求得四边形ABCD一边的长,从而可以求得四边形ABCD的周长.21·cn·jy·com
【解答】解:由题意可得,
AD=2+ ( http: / / www.21cnjy.com )×2=2+2 ( http: / / www.21cnjy.com ),
∴四边形ABCD的周长是:4×(2+2 ( http: / / www.21cnjy.com ))=8+8 ( http: / / www.21cnjy.com ),
故答案为:8+8 ( http: / / www.21cnjy.com ).
16.(2017 绥化)半径为2的圆内接正三角形,正四边形,正六边形的边心距之比为 1: ( http: / / www.21cnjy.com ): ( http: / / www.21cnjy.com ) .
【分析】根据题意可以求得半径为2的圆内接正三角形,正四边形,正六边形的边心距,从而可以求得它们的比值.2·1·c·n·j·y
【解答】解:由题意可得,
正三角形的边心距是:2×sin30°=2× ( http: / / www.21cnjy.com )=1,
正四边形的边心距是:2×sin45°=2× ( http: / / www.21cnjy.com ),
正六边形的边心距是:2×sin60°=2× ( http: / / www.21cnjy.com ),
∴半径为2的圆内接正三角形,正四边形,正六边形的边心距之比为:1: ( http: / / www.21cnjy.com ): ( http: / / www.21cnjy.com ),
故答案为:1: ( http: / / www.21cnjy.com ): ( http: / / www.21cnjy.com ).
三.解答题(共20分)
17.(8分)(2017 河南模拟 ( http: / / www.21cnjy.com ))如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s).
(1)求证:四边形PEQB为平行四边形;
(2)填空:
①当t= 2 s时,四边形PBQE为菱形;
②当t= 0或4 s时,四边形PBQE为矩形.
( http: / / www.21cnjy.com )
【分析】(1)只要证明△ABP≌△DEQ(SAS),可得BP=EQ,同理PE=BQ,由此即可证明;
(2)①当PA=PF,QC=QD时,四边形PBEQ是菱形时,此时t=2s;
②当t=0时,∠EPF=∠PEF=30° ( http: / / www.21cnjy.com ),推出∠BPE=120°﹣30°=90°,推出此时四边形PBQE是矩形.当t=4时,同法可知∠BPE=90°,此时四边形PBQE是矩形;
【解答】(1)证明:∵正六边形ABCDEF内接于⊙O,
∴AB=BC=CD=DE=EF=FA,∠A=∠ABC=∠C=∠D=∠DEF=∠F,
∵点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,
∴AP=DQ=t,PF=QC=4﹣t,
在△ABP和△DEQ中,
( http: / / www.21cnjy.com ),
∴△ABP≌△DEQ(SAS),
∴BP=EQ,同理可证PE=QB,
∴四边形PEQB是平行四边形.
(2)解:①当PA=PF,QC=QD时,四边形PBEQ是菱形时,此时t=2s.
②当t=0时,∠EPF=∠PEF=30°,
∴∠BPE=120°﹣30°=90°,
∴此时四边形PBQE是矩形.
当t=4时,同法可知∠BPE=90°,此时四边形PBQE是矩形.
综上所述,t=0s或4s时,四边形PBQE是矩形.
故答案为2s,0s或4s.
( http: / / www.21cnjy.com )
18.(12分)(2017 武汉模拟)如图,正五边形ABCDE中.
( http: / / www.21cnjy.com )
(1)AC与BE相交于P,求证:四边形PEDC为菱形;
(2)延长DC、AE交于M点,连BM交CE于N,求证:CN=EP;
(3)若正五边形边长为2,直接写出AD的长为 ( http: / / www.21cnjy.com )+1 .
【分析】(1)只要证明∠DCB+∠CBE=180°,可得CD∥BE,同法可证AC∥ED,由此即可证明;【来源:21·世纪·教育·网】
(2)如图2中,连接AN.首先证明CN=AN,再证明△PAE≌△NEA,即可解决问题;
(3)如图3中.在AD上取一点W,使得AW=WE.设AW=x.由△AWE∽△AED,可得AE2=AW AD,构建方程即可解决问题;
【解答】(1)证明:如图1中,
( http: / / www.21cnjy.com )
∵五边形ABCDE是正五边形,
∴∠BCD=∠BAE=108°,
∵AB=AE,
∴∠ABE=∠AEB=36°,
∴∠CBE=72°,
∴∠DCB+∠CBE=180°,
∴CD∥BE,
同法可证,AC∥DE,
∴∴四边形PEDC是平行四边形,
∵CD=DE,
∴四边形PEDC是菱形;
(2)证明:如图2中,连接AN.
( http: / / www.21cnjy.com )
∵∠MCA=∠MAC=72°,
∴MC=MA,
∵BC=BA,
∴BM垂直平分线段AC,
∴NC=NA,
∴∠NCA=∠NAC=∠CEP=36°,
∵∠PAE=∠NEA=72°,
∴∠PEA=∠NAE=36°,
∵AE=EA,
∴△PAE≌△NEA,
∴AN=PE,
∴CN=PE.
(3)解:如图3中.在AD上取一点W,使得AW=WE.设AW=x.
( http: / / www.21cnjy.com )
∵∠A=∠D=∠AEW=36°,
∴∠DWE=∠DEW=72°,
∴DW=DE=2,
∵∠A=∠A,∠AEW=∠D,
∴△AWE∽△AED,
∴AE2=AW AD,
∴22=x(x+2),
解得x= ( http: / / www.21cnjy.com )﹣1,
∴AD=2+x= ( http: / / www.21cnjy.com )+1,
故答案为 ( http: / / www.21cnjy.com )+1.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
3.8 圆内接正多边形检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
1.(2017 沈阳)正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.2 C.2 ( http: / / www.21cnjy.com ) D.2 ( http: / / www.21cnjy.com )
2.(2017 株洲)下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
3.(2017 河北)已知正方形MNOK ( http: / / www.21cnjy.com )和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使K ( http: / / www.21cnjy.com )M边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
( http: / / www.21cnjy.com )
A.1.4 B.1.1 C.0.8 D.0.5
4.(2017 滨州)若正方形的外接圆半径为2,则其内切圆半径为( )
A. ( http: / / www.21cnjy.com ) B.2 ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.1
5.(2017 达州)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )21*cnjy*com
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
6.(2017 日照)下列说法正确的是( )
A.圆内接正六边形的边长与该圆的半径相等
B.在平面直角坐标系中,不同的坐标可以表示同一点
C.一元二次方程ax2+bx+c=0(a≠0)一定有实数根
D.将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等
7.(2017 兰州)如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A.π+1 B.π+2 C.π﹣1 D.π﹣2
8.(2017 莱芜)如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣ ( http: / / www.21cnjy.com );③(S四边形CDEF)2=9+2 ( http: / / www.21cnjy.com );④DF2﹣DG2=7﹣2 ( http: / / www.21cnjy.com ).其中结论正确的个数是( )
( http: / / www.21cnjy.com )
A.1 B.2 C.3 D.4
9.(2017 石家庄模拟)如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y= ( http: / / www.21cnjy.com )位于第一象限的图象上,则k的值为( )21教育网
( http: / / www.21cnjy.com )
A.9 ( http: / / www.21cnjy.com ) B.9 ( http: / / www.21cnjy.com ) C.3 ( http: / / www.21cnjy.com ) D.3 ( http: / / www.21cnjy.com )
10.(2017 西固区校级模拟)周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是( )
A.S3>S4>S6 B.S6>S4>S3 C.S6>S3>S4 D.S4>S6>S3
二.填空题(每小题5分,共30分)
11.(2017 宜宾)如图,⊙O的内接正五边形ABCDE的对角线AD与BE相交于点G,AE=2,则EG的长是 .
( http: / / www.21cnjy.com )
12.(2017 凉山州)如图,P、Q分别是⊙O的内接正五边形的边AB、BC上的点,BP=CQ,则∠POQ= .
( http: / / www.21cnjy.com )
13.(2017 济宁)如图,正六边形A1 ( http: / / www.21cnjy.com )B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是 .
( http: / / www.21cnjy.com )
14.(2017 台州)如 ( http: / / www.21cnjy.com )图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是 .
( http: / / www.21cnjy.com )
15.(2017 玉林)如图,在边长为 ( http: / / www.21cnjy.com )2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是 .
( http: / / www.21cnjy.com )
16.(2017 绥化)半径为2的圆内接正三角形,正四边形,正六边形的边心距之比为 .
三.解答题(共20分)
17.(8分)(2017 河南模拟 ( http: / / www.21cnjy.com ))如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s).
(1)求证:四边形PEQB为平行四边形;
(2)填空:
①当t= s时,四边形PBQE为菱形;
②当t= s时,四边形PBQE为矩形.
( http: / / www.21cnjy.com )
18.(12分)(2017 武汉模拟)如图,正五边形ABCDE中.
( http: / / www.21cnjy.com )
(1)AC与BE相交于P,求证:四边形PEDC为菱形;
(2)延长DC、AE交于M点,连BM交CE于N,求证:CN=EP;
(3)若正五边形边长为2,直接写出AD的长为 .
3.8 圆内接正多边形检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017 沈阳)正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.2 C.2 ( http: / / www.21cnjy.com ) D.2 ( http: / / www.21cnjy.com )
【分析】连接OA,OB,根据等边三角形的性质可得⊙O的半径,进而可得出结论.
【解答】解:连接OB,OC,
∵多边形ABCDEF是正六边形,
∴∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴OB=BC,
∵正六边形的周长是12,
∴BC=2,
∴⊙O的半径是2,
故选B.
( http: / / www.21cnjy.com )
2.(2017 株洲)下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
【分析】根据正多边形的中心角的度数即可得到结论.
【解答】解:∵正三角形一条边所对的圆心角是360°÷3=120°,
正方形一条边所对的圆心角是360°÷4=90°,
正五边形一条边所对的圆心角是360°÷5=72°,
正六边形一条边所对的圆心角是360°÷6=60°,
∴一条边所对的圆心角最大的图形是正三角形,
故选A.
3.(2017 河北)已知正方形M ( http: / / www.21cnjy.com )NOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:
将正方形在正六边形中绕点B顺时针旋转,使KM ( http: / / www.21cnjy.com )边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
( http: / / www.21cnjy.com )
A.1.4 B.1.1 C.0.8 D.0.5
【分析】如图,在这样连续6次旋转的过程中,点M的运动轨迹是图中的红线,观察图象可知点B,M间的距离大于等于2﹣ ( http: / / www.21cnjy.com )小于等于1,由此即可判断.
【解答】解:如图,在这样连续6次旋转的过程中,点M的运动轨迹是图中的红线,
观察图象可知点B,M间的距离大于等于2﹣ ( http: / / www.21cnjy.com )小于等于1,
故选C.
( http: / / www.21cnjy.com )
4.(2017 滨州)若正方形的外接圆半径为2,则其内切圆半径为( )
A. ( http: / / www.21cnjy.com ) B.2 ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.1
【分析】根据题意画出图形,再由正方形及等腰直角三角形的性质求解即可.
【解答】解:如图所示,连接OA、OE,
∵AB是小圆的切线,
∴OE⊥AB,
∵四边形ABCD是正方形,
∴AE=OE,
∴△AOE是等腰直角三角形,
∴OE= ( http: / / www.21cnjy.com )OA= ( http: / / www.21cnjy.com ).
故选A.
( http: / / www.21cnjy.com )
5.(2017 达州)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】由于内接正三角形、 ( http: / / www.21cnjy.com )正方形、正六边形是特殊内角的多边形,可构造直角三角形分别求出边心距的长,由勾股定理逆定理可得该三角形是直角三角形,进而可得其面积.
【解答】解:如图1,
( http: / / www.21cnjy.com )
∵OC=2,
∴OD=2×sin30°=1;
如图2,
( http: / / www.21cnjy.com )
∵OB=2,
∴OE=2×sin45°= ( http: / / www.21cnjy.com );
如图3,
( http: / / www.21cnjy.com )
∵OA=2,
∴OD=2×cos30°= ( http: / / www.21cnjy.com ),
则该三角形的三边分别为:1, ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),
∵(1)2+( ( http: / / www.21cnjy.com ))2=( ( http: / / www.21cnjy.com ))2,
∴该三角形是直角三角形,
∴该三角形的面积是: ( http: / / www.21cnjy.com )×1× ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
故选:A.
6.(2017 日照)下列说法正确的是( )
A.圆内接正六边形的边长与该圆的半径相等
B.在平面直角坐标系中,不同的坐标可以表示同一点
C.一元二次方程ax2+bx+c=0(a≠0)一定有实数根
D.将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等
【分析】根据正多边形和圆的关系、一元二次方程根的判别式、点的坐标以及旋转变换的性质进行判断即可.
【解答】解:如图∠AOB= ( http: / / www.21cnjy.com )=60°,OA=OB,
∴△AOB是等边三角形,
∴AB=OA,
∴圆内接正六边形的边长与该圆的半径相等,A正确;
在平面直角坐标系中,不同的坐标可以表示不同一点,B错误;
一元二次方程ax2+bx+c=0(a≠0)不一定有实数根,C错误;
根据旋转变换的性质可知,将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE全等,D错误;2-1-c-n-j-y
故选:A.
( http: / / www.21cnjy.com )
7.(2017 兰州)如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A.π+1 B.π+2 C.π﹣1 D.π﹣2
【分析】根据对称性可知阴影部分的面积等于圆的面积减去正方形的 ( http: / / www.21cnjy.com ),求出圆内接正方形的边长,即可求解.
【解答】解:连接AO,DO,
∵ABCD是正方形,
∴∠AOD=90°,
AD= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com ),
圆内接正方形的边长为2 ( http: / / www.21cnjy.com ),所以阴影部分的面积= ( http: / / www.21cnjy.com )[4π﹣(2 ( http: / / www.21cnjy.com ))2]=(π﹣2)cm2.
故选D.
( http: / / www.21cnjy.com )
8.(2017 莱芜)如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣ ( http: / / www.21cnjy.com );③(S四边形CDEF)2=9+2 ( http: / / www.21cnjy.com );④DF2﹣DG2=7﹣2 ( http: / / www.21cnjy.com ).其中结论正确的个数是( )【版权所有:21教育】
( http: / / www.21cnjy.com )
A.1 B.2 C.3 D.4
【分析】①先根据正五方形ABCDE的性质得:∠ABC=180°﹣ ( http: / / www.21cnjy.com )=108°,由等边对等角可得:∠BAC=∠ACB=36°,再利用角相等求BC=CF=CD,得∠CDF=∠CFD= ( http: / / www.21cnjy.com )=54°,可得∠FDG=18°;
②证明△ABF∽△ACB,得 ( http: / / www.21cnjy.com ),代入可得FG的长;
③如图1,先证明四边形CDEF是平行四边形,根据平行四边形的面积公式可得:(S四边形CDEF)2=EF2 DM2=4× ( http: / / www.21cnjy.com )=10+2 ( http: / / www.21cnjy.com );
④如图2, CDEF是菱形,先计算EC=BE=4﹣FG=1+ ( http: / / www.21cnjy.com ),由S四边形CDEF= ( http: / / www.21cnjy.com )FD EC=2× ( http: / / www.21cnjy.com ),可得FD2=10﹣2 ( http: / / www.21cnjy.com ),计算可得结论.
【解答】解:①∵五方形ABCDE是正五边形,
∴AB=BC,∠ABC=180°﹣ ( http: / / www.21cnjy.com )=108°,
∴∠BAC=∠ACB=36°,
∴∠ACD=108°﹣36°=72°,
同理得:∠ADE=36°,
∵∠BAE=108°,AB=AE,
∴∠ABE=36°,
∴∠CBF=108°﹣36°=72°,
∴BC=FC,
∵BC=CD,
∴CD=CF,
∴∠CDF=∠CFD= ( http: / / www.21cnjy.com )=54°,
∴∠FDG=∠CDE﹣∠CDF﹣∠ADE=108°﹣54°﹣36°=18°;
所以①正确;
②∵∠ABE=∠ACB=36°,∠BAC=∠BAF,
∴△ABF∽△ACB,
∴ ( http: / / www.21cnjy.com ),
∴AB ED=AC EG,
∵AB=ED=2,AC=BE=BG+EF﹣FG=2AB﹣FG=4﹣FG,EG=BG﹣FG=2﹣FG,
∴22=(2﹣FG)(4﹣FG),
∴FG=3+ ( http: / / www.21cnjy.com )>2(舍),FG=3﹣ ( http: / / www.21cnjy.com );
所以②正确;
③如图1,∵∠EBC=72°,∠BCD=108°,
∴∠EBC+∠BCD=180°,
∴EF∥CD,
∵EF=CD=2,
∴四边形CDEF是平行四边形,
过D作DM⊥EG于M,
∵DG=DE,
∴EM=MG= ( http: / / www.21cnjy.com )EG= ( http: / / www.21cnjy.com )(EF﹣FG)= ( http: / / www.21cnjy.com )(2﹣3+ ( http: / / www.21cnjy.com ))= ( http: / / www.21cnjy.com ),
由勾股定理得:DM= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴(S四边形CDEF)2=EF2 DM2=4× ( http: / / www.21cnjy.com )=10+2 ( http: / / www.21cnjy.com );
所以③不正确;
④如图2,连接EC,
∵EF=ED,
∴ CDEF是菱形,
∴FD⊥EC,
∵EC=BE=4﹣FG=4﹣(3﹣ ( http: / / www.21cnjy.com ))=1+ ( http: / / www.21cnjy.com ),
∴S四边形CDEF= ( http: / / www.21cnjy.com )FD EC=2× ( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com )×FD×(1+ ( http: / / www.21cnjy.com ))= ( http: / / www.21cnjy.com ),
FD2=10﹣2 ( http: / / www.21cnjy.com ),
∴DF2﹣DG2=10﹣2 ( http: / / www.21cnjy.com )﹣4=6﹣2 ( http: / / www.21cnjy.com ),
所以④不正确;
本题正确的有两个,
故选B.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
9.(2017 石家庄模拟)如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y= ( http: / / www.21cnjy.com )位于第一象限的图象上,则k的值为( )21世纪教育网版权所有
( http: / / www.21cnjy.com )
A.9 ( http: / / www.21cnjy.com ) B.9 ( http: / / www.21cnjy.com ) C.3 ( http: / / www.21cnjy.com ) D.3 ( http: / / www.21cnjy.com )
【分析】连接OB,过B作BG⊥OA于G,得出等边三角形OBA,求出OB,求出OG、BG,得出B的坐标,即可去除答案.21cnjy.com
【解答】解: ( http: / / www.21cnjy.com )
连接OB,过B作BG⊥OA于G,
∵ABCDEF是正六边形,
∴∠AOB=60°,
∵OB=OA,
∴△AOB是等边三角形,
∴OB=OA=AB=6,
∵BG⊥OA,
∴∠BGO=90°,
∴∠OBG=30°,
∴OG= ( http: / / www.21cnjy.com )OB=3,由勾股定理得:BG=3 ( http: / / www.21cnjy.com ),
即B的坐标是(3,3 ( http: / / www.21cnjy.com )),
∵B点在反比例函数y= ( http: / / www.21cnjy.com )上,
∴k=3×3 ( http: / / www.21cnjy.com )=9 ( http: / / www.21cnjy.com ),
故选B.
10.(2017 西固区校级模拟)周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是( )www.21-cn-jy.com
A.S3>S4>S6 B.S6>S4>S3 C.S6>S3>S4 D.S4>S6>S3
【分析】先根据题意画出图形设出正六边形的边长,再根据正三角形、正方形、正六边形的周长都相等求出各图形的边长,再分别求出其面积即可.
【解答】解:设正六边形的边长为a,如图所示,
则正△ABC的边长为2a,正方形ABCD的边长为 ( http: / / www.21cnjy.com ).
如图(1),过A作AD⊥BC,D为垂足;
∵△ABC是等边三角形,BC=2a,
∴BD=a,由勾股定理得,AD= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )a,
∴S3=S△ABC= ( http: / / www.21cnjy.com )BC AD= ( http: / / www.21cnjy.com )×2a× ( http: / / www.21cnjy.com )a= ( http: / / www.21cnjy.com )a2≈1.73a2.
如图(2),∵四边形ABCD是正方形,
∴AB= ( http: / / www.21cnjy.com ),
∴S4=S□ABCD=AB2= ( http: / / www.21cnjy.com )× ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )a2≈2.25a2.
如图(3),过O作OG⊥BC,G为垂足,
∵六边形ABCDEF是正六边形,
∴∠BOC= ( http: / / www.21cnjy.com )=60°,
∴∠BOG=30°,OG= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )a.
∴S△BOC= ( http: / / www.21cnjy.com )× ( http: / / www.21cnjy.com )a×a= ( http: / / www.21cnjy.com )a2,
∴S6=6S△BOC=6× ( http: / / www.21cnjy.com )a= ( http: / / www.21cnjy.com )a2≈2.59a2.
∵2.59a2>2.25a2>1.73a2.
∴S6>S4>S3.
故选:B.
( http: / / www.21cnjy.com )
二.填空题(每小题5分,共30分)
11.(2017 宜宾)如图,⊙O的内接正五边形ABCDE的对角线AD与BE相交于点G,AE=2,则EG的长是 ( http: / / www.21cnjy.com )﹣1 .21·世纪*教育网
( http: / / www.21cnjy.com )
【分析】在⊙O的内接正五 ( http: / / www.21cnjy.com )边形ABCDE中,设EG=x,易知:∠AEB=∠ABE=∠EAG=36°,∠BAG=∠AGB=72°,推出AB=BG=AE=2,由△AEG∽△BEA,可得AE2=EG EB,可得22=x(x+2),解方程即可.www-2-1-cnjy-com
【解答】解:在⊙O的内接正五边形ABCDE中,设EG=x,
易知:∠AEB=∠ABE=∠EAG=36°,
∠BAG=∠AGB=72°,
∴AB=BG=AE=2,
∵∠AEG=∠AEB,∠EAG=∠EBA,
∴△AEG∽△BEA,
∴AE2=EG EB,
∴22=x(x+2),
解得x=﹣1+ ( http: / / www.21cnjy.com )或﹣1﹣ ( http: / / www.21cnjy.com ),
∴EG= ( http: / / www.21cnjy.com )﹣1,
故答案为 ( http: / / www.21cnjy.com )﹣1.
12.(2017 凉山州)如图,P、Q分别是⊙O的内接正五边形的边AB、BC上的点,BP=CQ,则∠POQ= 72° .【出处:21教育名师】
( http: / / www.21cnjy.com )
【分析】连接OA、OB、OC,证明△OBP≌△OCQ,根据全等三角形的性质得到∠BOP=∠COQ,结合图形计算即可.21教育名师原创作品
【解答】解:连接OA、OB、OC,
∵五边形ABCDE是⊙O的内接正五边形,
∴∠AOB=∠BOC=72°,
∵OA=OB,OB=OC,
∴∠OBA=∠OCB=54°,
在△OBP和△OCQ中,
( http: / / www.21cnjy.com ),
∴△OBP≌△OCQ,
∴∠BOP=∠COQ,
∵∠AOB=∠AOP+∠BOP,∠BOC=∠BOQ+∠QOC,
∴∠BOP=∠QOC,
∵∠POQ=∠BOP+∠BOQ,∠BOC=∠BOQ+∠QOC,
∴∠POQ=∠BOC=72°.
故答案为:72°.
( http: / / www.21cnjy.com )
13.(2017 济宁)如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是 ( http: / / www.21cnjy.com ) .21*cnjy*com
( http: / / www.21cnjy.com )
【分析】由正六边形的性质得:∠A1B1B2=90°,∠B1A1B2=30°,A1A2=A2B2,由直角三角形的性质得出B1B2= ( http: / / www.21cnjy.com )A1B1= ( http: / / www.21cnjy.com ),A2B2= ( http: / / www.21cnjy.com )A1B2=B1B2= ( http: / / www.21cnjy.com ),由相似多边形的性质得出正六边形A2B2C2D2E2F2的面积:正六边形A1B1C1D1E1F1的面积= ( http: / / www.21cnjy.com ),求出正六边形A1B1C1D1E1F1的面积= ( http: / / www.21cnjy.com ),得出正六边形A2B2C2D2E2F2的面积,同理得出正六边形A4B4C4D4E4F4的面积.
【解答】解:由正六边形的性质得:∠A1B1B2=90°,∠B1A1B2=30°,A1A2=A2B2,
∴B1B2= ( http: / / www.21cnjy.com )A1B1= ( http: / / www.21cnjy.com ),
∴A2B2= ( http: / / www.21cnjy.com )A1B2=B1B2= ( http: / / www.21cnjy.com ),
∵正六边形A1B1C1D1E1F1∽正六边形A2B2C2D2E2F2,
∴正六边形A2B2C2D2E2F2的面积:正六边形A1B1C1D1E1F1的面积=( ( http: / / www.21cnjy.com ))2= ( http: / / www.21cnjy.com ),
∵正六边形A1B1C1D1E1F1的面积=6× ( http: / / www.21cnjy.com )×1× ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴正六边形A2B2C2D2E2F2的面积= ( http: / / www.21cnjy.com )× ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
同理:正六边形A4B4C4D4E4F4的面积=( ( http: / / www.21cnjy.com ))3× ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com );
故答案为: ( http: / / www.21cnjy.com ).
14.(2017 台州)如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是 ( http: / / www.21cnjy.com )≤a≤3﹣ ( http: / / www.21cnjy.com ) .
( http: / / www.21cnjy.com )
【分析】当正方形ABCD的顶点A、B、 ( http: / / www.21cnjy.com )C、D在正六边形的边上时,正方形的边长的值最大,解直角三角形得到a,当正方形ABCD的对角线AC在正六边形一组平行的对边的中点上时,正方形边长a的值最小,AC是正方形的对角线,解直角三角形即可得到结论.【来源:21cnj*y.co*m】
【解答】解:①当正方形ABCD的对角线AC在正六边形一组平行的对边的中点上时,
正方形边长a的值最小,AC是正方形的对角线,
∴AC=A′D= ( http: / / www.21cnjy.com ),
∴a= ( http: / / www.21cnjy.com ),
②当正方形ABCD的四个顶点都在正六边形的边上时,正方形边长a的值最大,AC是正方形的对角线AC,
设A′(t, ( http: / / www.21cnjy.com ))时,正方形的边长最大,
∵OB′⊥OA′,
∴B′(﹣ ( http: / / www.21cnjy.com ),t),
设直线MN的解析式为y=kx+b,M(﹣1,0),N(﹣ ( http: / / www.21cnjy.com ),﹣ ( http: / / www.21cnjy.com )),
∴ ( http: / / www.21cnjy.com ),
∴ ( http: / / www.21cnjy.com ),
∴直线MN的解析式为y=﹣ ( http: / / www.21cnjy.com )x﹣ ( http: / / www.21cnjy.com ),
将B′(﹣ ( http: / / www.21cnjy.com ),t)代入得t= ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com ),
此时,A′B′取最大值,
∴a= ( http: / / www.21cnjy.com )=3﹣ ( http: / / www.21cnjy.com ),
∴正方形边长a的取值范围是: ( http: / / www.21cnjy.com )≤a≤3﹣ ( http: / / www.21cnjy.com ),
故答案为: ( http: / / www.21cnjy.com )≤a≤3﹣ ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
15.(2017 玉林)如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是 8+8 ( http: / / www.21cnjy.com ) .
( http: / / www.21cnjy.com )
【分析】根据题意可知形成的四个小的直角 ( http: / / www.21cnjy.com )三角形全等,并且四个都是等腰直角三角形,从而可以求得四边形ABCD一边的长,从而可以求得四边形ABCD的周长.21·cn·jy·com
【解答】解:由题意可得,
AD=2+ ( http: / / www.21cnjy.com )×2=2+2 ( http: / / www.21cnjy.com ),
∴四边形ABCD的周长是:4×(2+2 ( http: / / www.21cnjy.com ))=8+8 ( http: / / www.21cnjy.com ),
故答案为:8+8 ( http: / / www.21cnjy.com ).
16.(2017 绥化)半径为2的圆内接正三角形,正四边形,正六边形的边心距之比为 1: ( http: / / www.21cnjy.com ): ( http: / / www.21cnjy.com ) .
【分析】根据题意可以求得半径为2的圆内接正三角形,正四边形,正六边形的边心距,从而可以求得它们的比值.2·1·c·n·j·y
【解答】解:由题意可得,
正三角形的边心距是:2×sin30°=2× ( http: / / www.21cnjy.com )=1,
正四边形的边心距是:2×sin45°=2× ( http: / / www.21cnjy.com ),
正六边形的边心距是:2×sin60°=2× ( http: / / www.21cnjy.com ),
∴半径为2的圆内接正三角形,正四边形,正六边形的边心距之比为:1: ( http: / / www.21cnjy.com ): ( http: / / www.21cnjy.com ),
故答案为:1: ( http: / / www.21cnjy.com ): ( http: / / www.21cnjy.com ).
三.解答题(共20分)
17.(8分)(2017 河南模拟 ( http: / / www.21cnjy.com ))如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s).
(1)求证:四边形PEQB为平行四边形;
(2)填空:
①当t= 2 s时,四边形PBQE为菱形;
②当t= 0或4 s时,四边形PBQE为矩形.
( http: / / www.21cnjy.com )
【分析】(1)只要证明△ABP≌△DEQ(SAS),可得BP=EQ,同理PE=BQ,由此即可证明;
(2)①当PA=PF,QC=QD时,四边形PBEQ是菱形时,此时t=2s;
②当t=0时,∠EPF=∠PEF=30° ( http: / / www.21cnjy.com ),推出∠BPE=120°﹣30°=90°,推出此时四边形PBQE是矩形.当t=4时,同法可知∠BPE=90°,此时四边形PBQE是矩形;
【解答】(1)证明:∵正六边形ABCDEF内接于⊙O,
∴AB=BC=CD=DE=EF=FA,∠A=∠ABC=∠C=∠D=∠DEF=∠F,
∵点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,
∴AP=DQ=t,PF=QC=4﹣t,
在△ABP和△DEQ中,
( http: / / www.21cnjy.com ),
∴△ABP≌△DEQ(SAS),
∴BP=EQ,同理可证PE=QB,
∴四边形PEQB是平行四边形.
(2)解:①当PA=PF,QC=QD时,四边形PBEQ是菱形时,此时t=2s.
②当t=0时,∠EPF=∠PEF=30°,
∴∠BPE=120°﹣30°=90°,
∴此时四边形PBQE是矩形.
当t=4时,同法可知∠BPE=90°,此时四边形PBQE是矩形.
综上所述,t=0s或4s时,四边形PBQE是矩形.
故答案为2s,0s或4s.
( http: / / www.21cnjy.com )
18.(12分)(2017 武汉模拟)如图,正五边形ABCDE中.
( http: / / www.21cnjy.com )
(1)AC与BE相交于P,求证:四边形PEDC为菱形;
(2)延长DC、AE交于M点,连BM交CE于N,求证:CN=EP;
(3)若正五边形边长为2,直接写出AD的长为 ( http: / / www.21cnjy.com )+1 .
【分析】(1)只要证明∠DCB+∠CBE=180°,可得CD∥BE,同法可证AC∥ED,由此即可证明;【来源:21·世纪·教育·网】
(2)如图2中,连接AN.首先证明CN=AN,再证明△PAE≌△NEA,即可解决问题;
(3)如图3中.在AD上取一点W,使得AW=WE.设AW=x.由△AWE∽△AED,可得AE2=AW AD,构建方程即可解决问题;
【解答】(1)证明:如图1中,
( http: / / www.21cnjy.com )
∵五边形ABCDE是正五边形,
∴∠BCD=∠BAE=108°,
∵AB=AE,
∴∠ABE=∠AEB=36°,
∴∠CBE=72°,
∴∠DCB+∠CBE=180°,
∴CD∥BE,
同法可证,AC∥DE,
∴∴四边形PEDC是平行四边形,
∵CD=DE,
∴四边形PEDC是菱形;
(2)证明:如图2中,连接AN.
( http: / / www.21cnjy.com )
∵∠MCA=∠MAC=72°,
∴MC=MA,
∵BC=BA,
∴BM垂直平分线段AC,
∴NC=NA,
∴∠NCA=∠NAC=∠CEP=36°,
∵∠PAE=∠NEA=72°,
∴∠PEA=∠NAE=36°,
∵AE=EA,
∴△PAE≌△NEA,
∴AN=PE,
∴CN=PE.
(3)解:如图3中.在AD上取一点W,使得AW=WE.设AW=x.
( http: / / www.21cnjy.com )
∵∠A=∠D=∠AEW=36°,
∴∠DWE=∠DEW=72°,
∴DW=DE=2,
∵∠A=∠A,∠AEW=∠D,
∴△AWE∽△AED,
∴AE2=AW AD,
∴22=x(x+2),
解得x= ( http: / / www.21cnjy.com )﹣1,
∴AD=2+x= ( http: / / www.21cnjy.com )+1,
故答案为 ( http: / / www.21cnjy.com )+1.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
