3.9 弧长及扇形的面积一课一测
图片预览

文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
3.9 弧长及扇形的面积检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
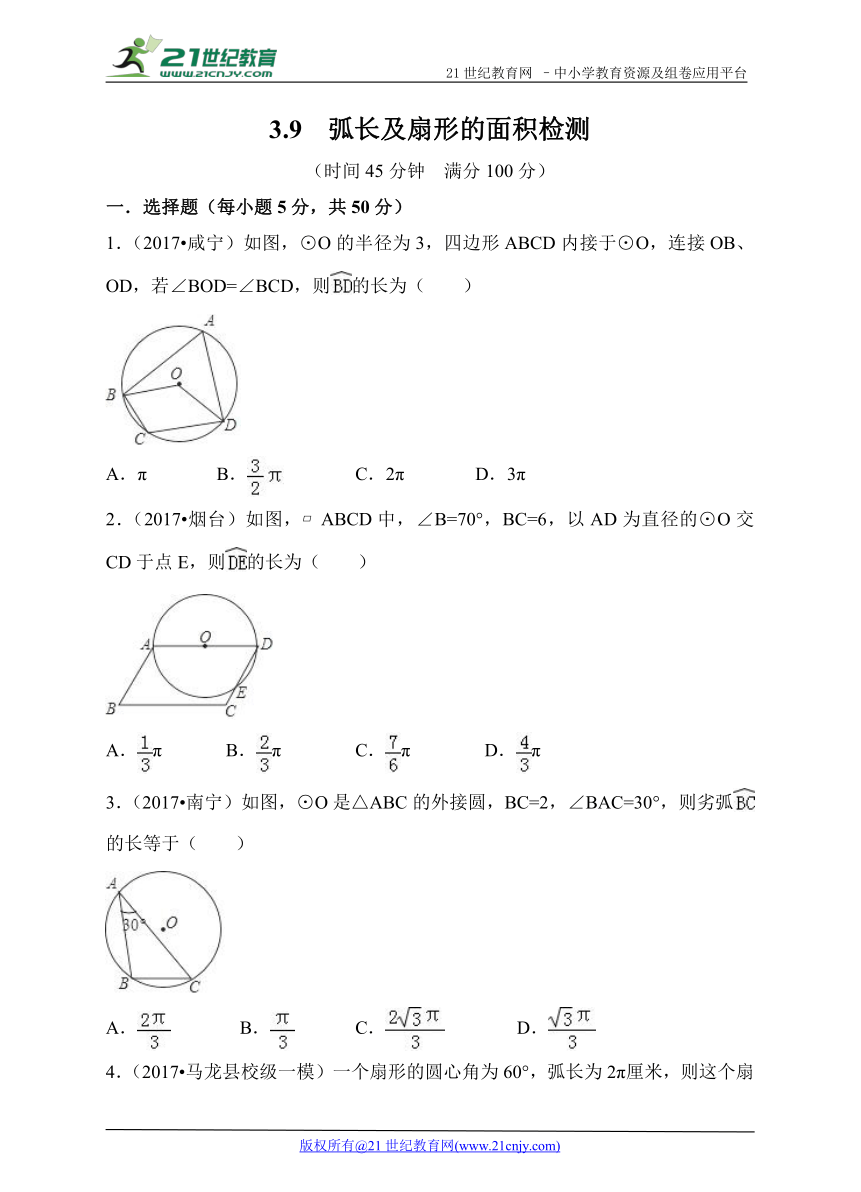
1.(2017 咸宁)如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则 ( http: / / www.21cnjy.com )的长为( )
( http: / / www.21cnjy.com )
A.π B. ( http: / / www.21cnjy.com ) C.2π D.3π
2.(2017 烟台)如图, ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则 ( http: / / www.21cnjy.com )的长为( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com )π B. ( http: / / www.21cnjy.com )π C. ( http: / / www.21cnjy.com )π D. ( http: / / www.21cnjy.com )π
3.(2017 南宁)如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧 ( http: / / www.21cnjy.com )的长等于( )21教育名师原创作品
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
4.(2017 马龙县校级一模)一个扇形的圆心角为60°,弧长为2π厘米,则这个扇形的半径为( )
A.6厘米 B.12厘米 C. ( http: / / www.21cnjy.com )厘米 D. ( http: / / www.21cnjy.com )厘米
5.(2017 满洲里市模拟)如图,⊙O的半径为1,A、B、C是圆周上的三点,∠BAC=36°,则劣弧BC的长是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
6.(2017 海曙区校级自主招生)如图,正方形ABCD的边AB=1, ( http: / / www.21cnjy.com )和 ( http: / / www.21cnjy.com )都是以1为半径的圆弧,则无阴影两部分的面积之差是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.1﹣ ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com )﹣1 D.1﹣ ( http: / / www.21cnjy.com )
7.(2017 北京模拟)如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.2 ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.1
8.(2017 张店区一模)如图,将△A ( http: / / www.21cnjy.com )BC绕点C按顺时针旋转60°得到△A′B′C,已知AC=6,BC=4,则线段AB扫过的图形的面积为( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com )π B. ( http: / / www.21cnjy.com )π C.6π D. ( http: / / www.21cnjy.com )π
9.(2017 海宁市校级模拟)如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为 ( http: / / www.21cnjy.com )π cm2,则扇形圆心角的度数为( )
( http: / / www.21cnjy.com )
A.120° B.140° C.150° D.160°
10.(2017 东河区二模)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二.填空题(每小题5分,共30分)
11.(2017 白银)如图,在△ABC中 ( http: / / www.21cnjy.com ),∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于 .(结果保留π)
( http: / / www.21cnjy.com )
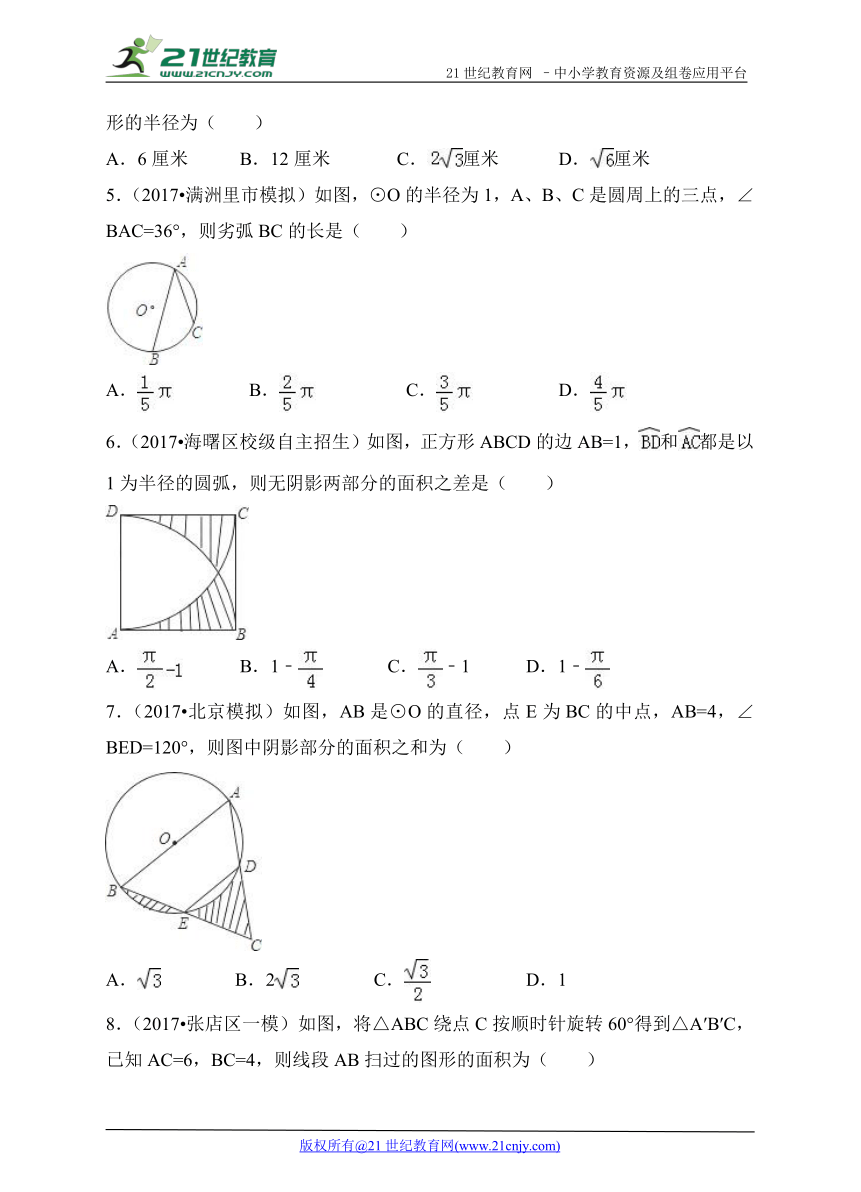
12.(2017 黔南州)如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则 ( http: / / www.21cnjy.com )的长为 .
( http: / / www.21cnjy.com )
13.(2017 聊城)如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中 ( http: / / www.21cnjy.com )的长为 .
( http: / / www.21cnjy.com )
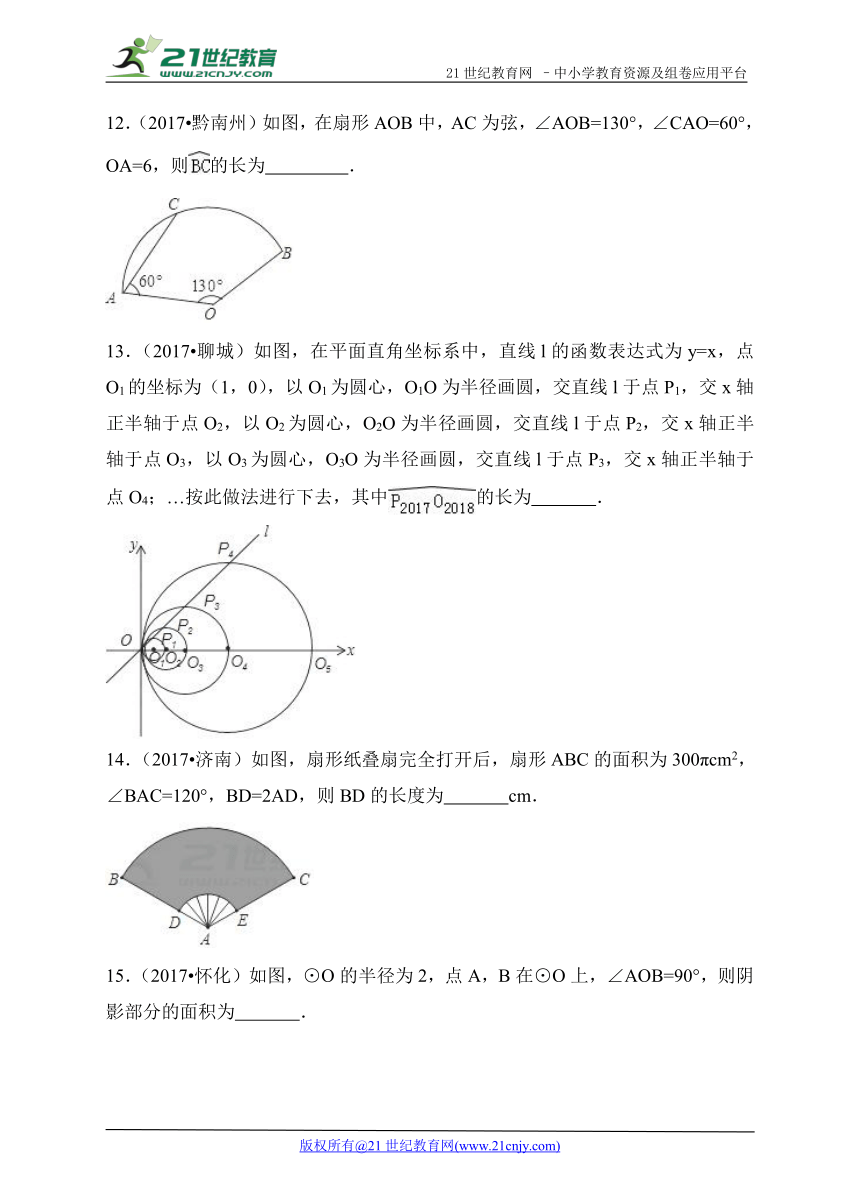
14.(2017 济南)如图,扇形纸叠扇完 ( http: / / www.21cnjy.com )全打开后,扇形ABC的面积为300πcm2,∠BAC=120°,BD=2AD,则BD的长度为 cm.21教育网
( http: / / www.21cnjy.com )
15.(2017 怀化)如图,⊙O的半径为2,点A,B在⊙O上,∠AOB=90°,则阴影部分的面积为 .21cnjy.com
( http: / / www.21cnjy.com )
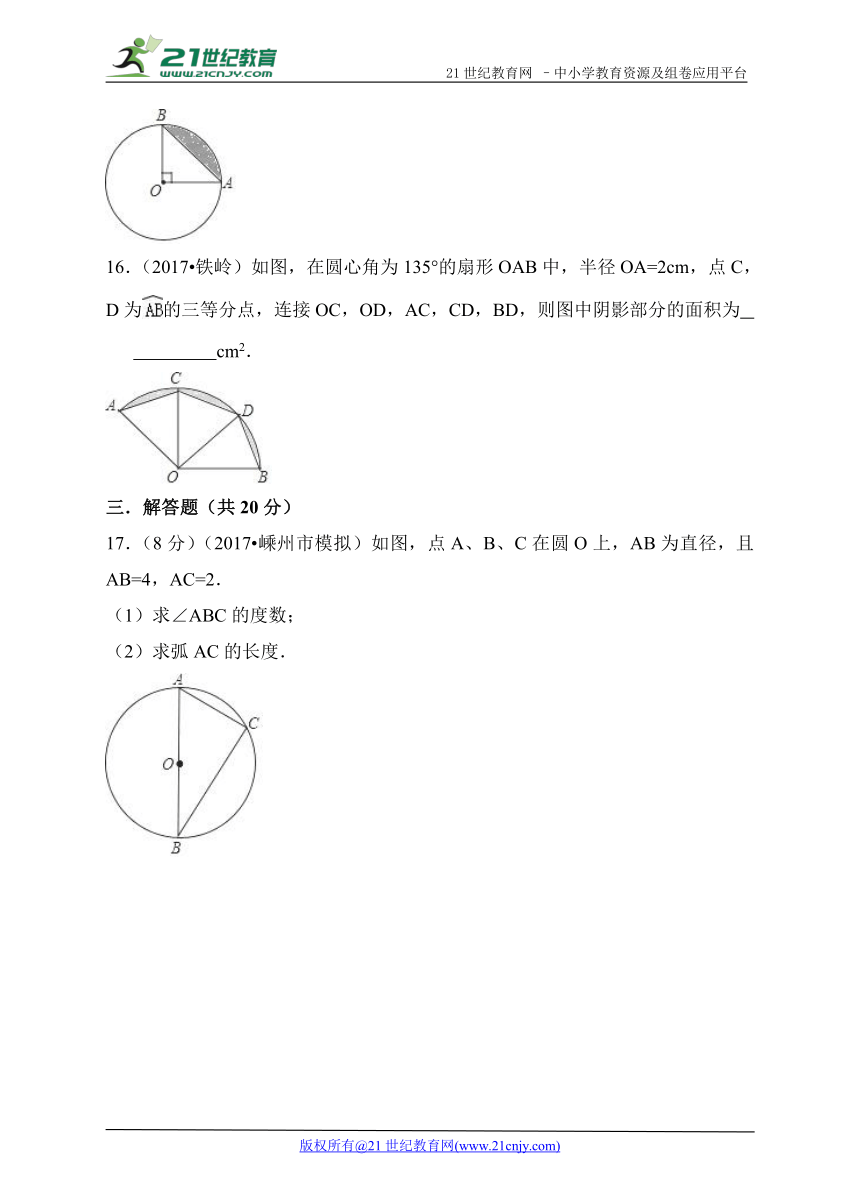
16.(2017 铁岭)如图,在圆心角为135°的扇形OAB中,半径OA=2cm,点C,D为 ( http: / / www.21cnjy.com )的三等分点,连接OC,OD,AC,CD,BD,则图中阴影部分的面积为
cm2.
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(8分)(2017 嵊州市模拟)如图,点A、B、C在圆O上,AB为直径,且AB=4,AC=2.
(1)求∠ABC的度数;
(2)求弧AC的长度.
( http: / / www.21cnjy.com )
18.(12分)(2016 扬中市一模)已知如图,在直角坐标系xOy中,点A,点B坐标分别为(﹣1,0),(0, ( http: / / www.21cnjy.com )),连结AB,OD由△AOB绕O点顺时针旋转60°而得.21世纪教育网版权所有
(1)求点C的坐标;
(2)△AOB绕点O顺时针旋转60°所扫过的面积;
(3)线段AB绕点O顺时针旋转60°所扫过的面积.
( http: / / www.21cnjy.com )
3.9 弧长及扇形的面积检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017 咸宁)如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则 ( http: / / www.21cnjy.com )的长为( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A.π B. ( http: / / www.21cnjy.com ) C.2π D.3π
【分析】由圆内接四边形的性质和圆周角定理求出∠A=60°,得出∠BOD=120°,再由弧长公式即可得出答案.
【解答】解:∵四边形ABCD内接于⊙O,
∴∠BCD+∠A=180°,
∵∠BOD=2∠A,∠BOD=∠BCD,
∴2∠A+∠A=180°,
解得:∠A=60°,
∴∠BOD=120°,
∴ ( http: / / www.21cnjy.com )的长= ( http: / / www.21cnjy.com )=2π;
故选:C.
2.(2017 烟台)如图, ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则 ( http: / / www.21cnjy.com )的长为( )【版权所有:21教育】
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com )π B. ( http: / / www.21cnjy.com )π C. ( http: / / www.21cnjy.com )π D. ( http: / / www.21cnjy.com )π
【分析】连接OE,由平行四 ( http: / / www.21cnjy.com )边形的性质得出∠D=∠B=70°,AD=BC=6,得出OA=OD=3,由等腰三角形的性质和三角形内角和定理求出∠DOE=40°,再由弧长公式即可得出答案.
【解答】解:连接OE,如图所示:
∵四边形ABCD是平行四边形,
∴∠D=∠B=70°,AD=BC=6,
∴OA=OD=3,
∵OD=OE,
∴∠OED=∠D=70°,
∴∠DOE=180°﹣2×70°=40°,
∴ ( http: / / www.21cnjy.com )的长= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com );
故选:B.
( http: / / www.21cnjy.com )
3.(2017 南宁)如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧 ( http: / / www.21cnjy.com )的长等于( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】连接OB、OC,利用圆周角定理求得∠BOC=60°,然后利用弧长公式l= ( http: / / www.21cnjy.com )来计算劣弧 ( http: / / www.21cnjy.com )的长.
【解答】解:如图,连接OB、OC,
∵∠BAC=30°,
∴∠BOC=2∠BAC=60°,
又OB=OC,
∴△OBC是等边三角形,
∴BC=OB=OC=2,
∴劣弧 ( http: / / www.21cnjy.com )的长为: ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
故选:A.
( http: / / www.21cnjy.com )
4.(2017 马龙县校级一模)一个扇形的圆心角为60°,弧长为2π厘米,则这个扇形的半径为( )【来源:21cnj*y.co*m】
A.6厘米 B.12厘米 C. ( http: / / www.21cnjy.com )厘米 D. ( http: / / www.21cnjy.com )厘米
【分析】代入弧长公式,解出扇形的半径R即可.
【解答】解:l= ( http: / / www.21cnjy.com ),
由题意得,2π= ( http: / / www.21cnjy.com ),
解得:R=6cm.
故选A.
5.(2017 满洲里市模拟)如图,⊙O的半径为1,A、B、C是圆周上的三点,∠BAC=36°,则劣弧BC的长是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】连接OB,OC,依据同弧所对的圆周角等于圆心角的一半,即可求得劣弧BC的圆心角的度数,然后利用弧长计算公式求解即可.21·世纪*教育网
【解答】解:连接OB,OC.
∠BOC=2∠BAC=2×36°=72°,
则劣弧BC的长是: ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )π.
故选B.
( http: / / www.21cnjy.com )
6.(2017 海曙区校级自主招生)如图,正方形ABCD的边AB=1, ( http: / / www.21cnjy.com )和 ( http: / / www.21cnjy.com )都是以1为半径的圆弧,则无阴影两部分的面积之差是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.1﹣ ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com )﹣1 D.1﹣ ( http: / / www.21cnjy.com )
【分析】图中1、2、3、4图形的面积和为正方形的面积,1、2和两个3的面积和是两个扇形的面积,因此两个扇形的面积的和﹣正方形的面积=无阴影两部分的面积之差,即 ( http: / / www.21cnjy.com )﹣1= ( http: / / www.21cnjy.com ).
【解答】解:如图:
正方形的面积=S1+S2+S3+S4;①
两个扇形的面积=2S3+S1+S2;②
②﹣①,得:S3﹣S4=S扇形﹣S正方形= ( http: / / www.21cnjy.com )﹣1= ( http: / / www.21cnjy.com ).
故选:A.
( http: / / www.21cnjy.com )
7.(2017 北京模拟)如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )21*cnjy*com
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.2 ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.1
【分析】首先证明△ABC是等边三角形.则△EDC是等边三角形,边长是2.而 ( http: / / www.21cnjy.com )和弦BE围成的部分的面积= ( http: / / www.21cnjy.com )和弦DE围成的部分的面积.由∠BOE=∠DOE,BE=ED推出S弓BE=S弓DE,这样可以得出S阴=S△EDC,据此即可求解.
【解答】解:连接AE,OD、OE.
∵AB是直径,
∴∠AEB=90°,
又∵∠BED=120°,
∴∠AED=30°,
∴∠AOD=2∠AED=60°.
∵OA=OD
∴△AOD是等边三角形,
∴∠OAD=60°,
∵点E为BC的中点,∠AEB=90°,
∴AB=AC,
∴△ABC是等边三角形,边长是4.△EDC是等边三角形,边长是2.
∴∠BOE=∠EOD=60°,
∴ ( http: / / www.21cnjy.com )和弦BE围成的部分的面积= ( http: / / www.21cnjy.com )和弦DE围成的部分的面积.
∴阴影部分的面积=S△EDC= ( http: / / www.21cnjy.com )×22= ( http: / / www.21cnjy.com ).
故选:A.
( http: / / www.21cnjy.com )
8.(2017 张店区一模)如图,将△ ( http: / / www.21cnjy.com )ABC绕点C按顺时针旋转60°得到△A′B′C,已知AC=6,BC=4,则线段AB扫过的图形的面积为( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com )π B. ( http: / / www.21cnjy.com )π C.6π D. ( http: / / www.21cnjy.com )π
【分析】根据图形可以得出AB扫过的 ( http: / / www.21cnjy.com )图形的面积=S扇形ACA′+S△ABC﹣S扇形BCB′﹣S△A′B′C,由旋转的性质就可以得出S△ABC=S△A′B′C就可以得出AB扫过的图形的面积=S扇形ACA′﹣S扇形BCB′求出其值即可.21·cn·jy·com
【解答】解:∵△ABC绕点C旋转60°得到△A′B′C,
∴△ABC≌△A′B′C,
∴S△ABC=S△A′B′C,∠BCB′=∠ACA′=60°.
∵AB扫过的图形的面积=S扇形ACA′+S△ABC﹣S扇形BCB′﹣S△A′B′C,
∴AB扫过的图形的面积=S扇形ACA′﹣S扇形BCB′,
∴AB扫过的图形的面积= ( http: / / www.21cnjy.com )×π×36﹣ ( http: / / www.21cnjy.com )×π×16= ( http: / / www.21cnjy.com )π.
故选D.
9.(2017 海宁市校级模拟)如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为 ( http: / / www.21cnjy.com )π cm2,则扇形圆心角的度数为( )2·1·c·n·j·y
( http: / / www.21cnjy.com )
A.120° B.140° C.150° D.160°
【分析】根据扇形的面积公式列方程即可得到结论.
【解答】解:∵OB=10cm,AB=20cm,
∴OA=OB+AB=30cm,
设扇形圆心角的度数为α,
∵纸面面积为 ( http: / / www.21cnjy.com )π cm2,
∴ ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )π,
∴α=150°,
故选C.
10.(2017 东河区二模)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】先根据平行线的性质得出∠1=∠2,再由正方形的性质得出∠ABD=45°,由S阴影=S扇形ABD+S扇形ENM即可得出结论.www-2-1-cnjy-com
【解答】解:∵AN∥BM,
∴∠1=∠2.
∵四边形ABCD是正方形,
∴∠ABD=45°,
∴S阴影=S扇形ABD+S扇形ENM= ( http: / / www.21cnjy.com )+ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
故选B.
( http: / / www.21cnjy.com )
二.填空题(每小题5分,共30分)
11.(2017 白银)如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于 ( http: / / www.21cnjy.com ) .(结果保留π)【出处:21教育名师】
( http: / / www.21cnjy.com )
【分析】先根据ACB=90°,AC=1,AB=2,得到∠ABC=30°,进而得出∠A=60°,再根据AC=1,即可得到弧CD的长.
【解答】解:∵∠ACB=90°,AC=1,AB=2,
∴∠ABC=30°,
∴∠A=60°,
又∵AC=1,
∴弧CD的长为 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
故答案为: ( http: / / www.21cnjy.com ).
12.(2017 黔南州)如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则 ( http: / / www.21cnjy.com )的长为 ( http: / / www.21cnjy.com )π .
( http: / / www.21cnjy.com )
【分析】连接OC,如图,利用等腰三角形的性质和三角形内角和可计算出∠AOC=60°,则∠BOC=70°,然后根据弧长公式计算 ( http: / / www.21cnjy.com )的长.21*cnjy*com
【解答】解:连接OC,如图,
∵OA=OC,
∴∠OCA=∠CAO=60°,
∴∠AOC=60°,
∴∠BOC=130°﹣60°=70°,
∴ ( http: / / www.21cnjy.com )的长= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )π.
故答案为 ( http: / / www.21cnjy.com )π.
( http: / / www.21cnjy.com )
13.(2017 聊城)如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中 ( http: / / www.21cnjy.com )的长为 22015π. .
( http: / / www.21cnjy.com )
【分析】连接P1O1,P2O2,P3O3,易求得PnOn垂直于x轴,可得 ( http: / / www.21cnjy.com ) 为 ( http: / / www.21cnjy.com )圆的周长,再找出圆半径的规律即可解题.
【解答】解:连接P1O1,P2O2,P3O3…
( http: / / www.21cnjy.com )
∵P1 是⊙O2上的点,
∴P1O1=OO1,
∵直线l解析式为y=x,
∴∠P1OO1=45°,
∴△P1OO1为等腰直角三角形,即P1O1⊥x轴,
同理,PnOn垂直于x轴,
∴ ( http: / / www.21cnjy.com ) 为 ( http: / / www.21cnjy.com )圆的周长,
∵以O1为圆心,O1O为半径画圆,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交x轴正半轴于点O3,以此类推,
∴OOn=2n﹣1,
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ) 2π OOn= ( http: / / www.21cnjy.com )π 2n﹣1=2n﹣2π,
当n=2017时, ( http: / / www.21cnjy.com )=22015π.
故答案为 22015π.
14.(2017 济南)如图,扇形 ( http: / / www.21cnjy.com )纸叠扇完全打开后,扇形ABC的面积为300πcm2,∠BAC=120°,BD=2AD,则BD的长度为 20 cm.
( http: / / www.21cnjy.com )
【分析】设AD=x,则AB=3x.由题意300π= ( http: / / www.21cnjy.com ),解方程即可.
【解答】解:设AD=x,则AB=3x.
由题意300π= ( http: / / www.21cnjy.com ),
解得x=10,
∴BD=2x=20cm.
故答案为20.
15.(2017 怀化)如图,⊙O的半径为2,点A,B在⊙O上,∠AOB=90°,则阴影部分的面积为 π﹣2 .2-1-c-n-j-y
( http: / / www.21cnjy.com )
【分析】根据∠AOB=90°,OA=OB可知△OAB是等腰直角三角形,根据S阴影=S扇形OAB﹣S△OAB即可得出结论.
【解答】解:∵∠AOB=90°,OA=OB,
∴△OAB是等腰直角三角形.
∵OA=2,
∴S阴影=S扇形OAB﹣S△OAB= ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com )×2×2=π﹣2.
故答案为π﹣2.
16.(2017 铁岭)如图,在圆心角为135°的扇形OAB中,半径OA=2cm,点C,D为 ( http: / / www.21cnjy.com )的三等分点,连接OC,OD,AC,CD,BD,则图中阴影部分的面积为 ( ( http: / / www.21cnjy.com )π﹣3 ( http: / / www.21cnjy.com )) cm2.www.21-cn-jy.com
( http: / / www.21cnjy.com )
【分析】易知△AOC≌△COD≌△DOB,如 ( http: / / www.21cnjy.com )图作DH⊥OB于H.求出DH,即可求出△DOB的面积,再根据阴影部分面积=扇形面积﹣三个三角形面积,计算即可.
【解答】解:如图作DH⊥OB于H.
( http: / / www.21cnjy.com )
∵点C,D为 ( http: / / www.21cnjy.com )的三等分点,∠AOB=135°,
∴∠AOC=∠COD=∠DOB=45°,
∴△ODH是等腰直角三角形,△AOC≌△COD≌△DOB,
∵OD=2,
∴DH=OH= ( http: / / www.21cnjy.com ),
∴S△ODB= ( http: / / www.21cnjy.com ) OB DH= ( http: / / www.21cnjy.com ),
∴S△AOC=S△COD=S△DOB= ( http: / / www.21cnjy.com ),
∴S阴= ( http: / / www.21cnjy.com )﹣3S△DOB=( ( http: / / www.21cnjy.com )π﹣3 ( http: / / www.21cnjy.com ))cm2,
故答案为( ( http: / / www.21cnjy.com )π﹣3 ( http: / / www.21cnjy.com ))cm2.
三.解答题(共20分)
17.(8分)(2017 嵊州市模拟)如图,点A、B、C在圆O上,AB为直径,且AB=4,AC=2.
(1)求∠ABC的度数;
(2)求弧AC的长度.
( http: / / www.21cnjy.com )
【分析】(1)根据圆周角定理得到∠C=90°,求得sin∠B= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),于是得到结论;
(2)根据圆周角定理得到∠AOC=60°,根据弧长公式即可得到结论.
【解答】解:(1)
∵AB为直径,
∴∠C=90°,
∵AB=4,AC=2,
∴sin∠B= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴∠ABC=30°;
(2)连接OC,
∵∠B=30°,
∴∠AOC=60°,
∴弧AC的长度= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )π.
18.(12分)(2016 扬中市一模)已知如图,在直角坐标系xOy中,点A,点B坐标分别为(﹣1,0),(0, ( http: / / www.21cnjy.com )),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
(1)求点C的坐标;
(2)△AOB绕点O顺时针旋转60°所扫过的面积;
(3)线段AB绕点O顺时针旋转60°所扫过的面积.
( http: / / www.21cnjy.com )
【分析】(1)如图1,过C作CE⊥OA于E,由点A,点B坐标分别为(﹣1,0),(0, ( http: / / www.21cnjy.com )),得到OA=1,OB= ( http: / / www.21cnjy.com ),根据旋转的性质得到∠AOC=∠BOD=60°,AO=OC=1,解直角三角形即可得到结论;
(2)根据三角形和扇形的面积公式即可得到结论;
(3)根据三角形和扇形的面积公式即可得到结论;
【解答】解:(1)如图1,过C作CE⊥OA于E,
∵点A,点B坐标分别为(﹣1,0),(0, ( http: / / www.21cnjy.com )),
∴OA=1,OB= ( http: / / www.21cnjy.com ),
∵△AOB绕点O顺时针旋转60°得到△COD,
∴∠AOC=∠BOD=60°,AO=OC=1,
∴OE= ( http: / / www.21cnjy.com )OC= ( http: / / www.21cnjy.com ),CE= ( http: / / www.21cnjy.com )OC= ( http: / / www.21cnjy.com ),
∴C(﹣ ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ));
(2)△AOB绕点O顺时针旋转60°所扫过的面积= ( http: / / www.21cnjy.com )+ ( http: / / www.21cnjy.com )+ ( http: / / www.21cnjy.com )× ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )π+ ( http: / / www.21cnjy.com );
(3)如图2,线段AB绕点O顺时针旋转60°所扫过的面积═( ( http: / / www.21cnjy.com )﹣1× ( http: / / www.21cnjy.com ))+( ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com ))+( ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com ))= ( http: / / www.21cnjy.com )π﹣ ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
3.9 弧长及扇形的面积检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
1.(2017 咸宁)如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则 ( http: / / www.21cnjy.com )的长为( )
( http: / / www.21cnjy.com )
A.π B. ( http: / / www.21cnjy.com ) C.2π D.3π
2.(2017 烟台)如图, ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则 ( http: / / www.21cnjy.com )的长为( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com )π B. ( http: / / www.21cnjy.com )π C. ( http: / / www.21cnjy.com )π D. ( http: / / www.21cnjy.com )π
3.(2017 南宁)如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧 ( http: / / www.21cnjy.com )的长等于( )21教育名师原创作品
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
4.(2017 马龙县校级一模)一个扇形的圆心角为60°,弧长为2π厘米,则这个扇形的半径为( )
A.6厘米 B.12厘米 C. ( http: / / www.21cnjy.com )厘米 D. ( http: / / www.21cnjy.com )厘米
5.(2017 满洲里市模拟)如图,⊙O的半径为1,A、B、C是圆周上的三点,∠BAC=36°,则劣弧BC的长是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
6.(2017 海曙区校级自主招生)如图,正方形ABCD的边AB=1, ( http: / / www.21cnjy.com )和 ( http: / / www.21cnjy.com )都是以1为半径的圆弧,则无阴影两部分的面积之差是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.1﹣ ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com )﹣1 D.1﹣ ( http: / / www.21cnjy.com )
7.(2017 北京模拟)如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.2 ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.1
8.(2017 张店区一模)如图,将△A ( http: / / www.21cnjy.com )BC绕点C按顺时针旋转60°得到△A′B′C,已知AC=6,BC=4,则线段AB扫过的图形的面积为( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com )π B. ( http: / / www.21cnjy.com )π C.6π D. ( http: / / www.21cnjy.com )π
9.(2017 海宁市校级模拟)如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为 ( http: / / www.21cnjy.com )π cm2,则扇形圆心角的度数为( )
( http: / / www.21cnjy.com )
A.120° B.140° C.150° D.160°
10.(2017 东河区二模)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二.填空题(每小题5分,共30分)
11.(2017 白银)如图,在△ABC中 ( http: / / www.21cnjy.com ),∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于 .(结果保留π)
( http: / / www.21cnjy.com )
12.(2017 黔南州)如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则 ( http: / / www.21cnjy.com )的长为 .
( http: / / www.21cnjy.com )
13.(2017 聊城)如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中 ( http: / / www.21cnjy.com )的长为 .
( http: / / www.21cnjy.com )
14.(2017 济南)如图,扇形纸叠扇完 ( http: / / www.21cnjy.com )全打开后,扇形ABC的面积为300πcm2,∠BAC=120°,BD=2AD,则BD的长度为 cm.21教育网
( http: / / www.21cnjy.com )
15.(2017 怀化)如图,⊙O的半径为2,点A,B在⊙O上,∠AOB=90°,则阴影部分的面积为 .21cnjy.com
( http: / / www.21cnjy.com )
16.(2017 铁岭)如图,在圆心角为135°的扇形OAB中,半径OA=2cm,点C,D为 ( http: / / www.21cnjy.com )的三等分点,连接OC,OD,AC,CD,BD,则图中阴影部分的面积为
cm2.
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(8分)(2017 嵊州市模拟)如图,点A、B、C在圆O上,AB为直径,且AB=4,AC=2.
(1)求∠ABC的度数;
(2)求弧AC的长度.
( http: / / www.21cnjy.com )
18.(12分)(2016 扬中市一模)已知如图,在直角坐标系xOy中,点A,点B坐标分别为(﹣1,0),(0, ( http: / / www.21cnjy.com )),连结AB,OD由△AOB绕O点顺时针旋转60°而得.21世纪教育网版权所有
(1)求点C的坐标;
(2)△AOB绕点O顺时针旋转60°所扫过的面积;
(3)线段AB绕点O顺时针旋转60°所扫过的面积.
( http: / / www.21cnjy.com )
3.9 弧长及扇形的面积检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017 咸宁)如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则 ( http: / / www.21cnjy.com )的长为( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A.π B. ( http: / / www.21cnjy.com ) C.2π D.3π
【分析】由圆内接四边形的性质和圆周角定理求出∠A=60°,得出∠BOD=120°,再由弧长公式即可得出答案.
【解答】解:∵四边形ABCD内接于⊙O,
∴∠BCD+∠A=180°,
∵∠BOD=2∠A,∠BOD=∠BCD,
∴2∠A+∠A=180°,
解得:∠A=60°,
∴∠BOD=120°,
∴ ( http: / / www.21cnjy.com )的长= ( http: / / www.21cnjy.com )=2π;
故选:C.
2.(2017 烟台)如图, ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则 ( http: / / www.21cnjy.com )的长为( )【版权所有:21教育】
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com )π B. ( http: / / www.21cnjy.com )π C. ( http: / / www.21cnjy.com )π D. ( http: / / www.21cnjy.com )π
【分析】连接OE,由平行四 ( http: / / www.21cnjy.com )边形的性质得出∠D=∠B=70°,AD=BC=6,得出OA=OD=3,由等腰三角形的性质和三角形内角和定理求出∠DOE=40°,再由弧长公式即可得出答案.
【解答】解:连接OE,如图所示:
∵四边形ABCD是平行四边形,
∴∠D=∠B=70°,AD=BC=6,
∴OA=OD=3,
∵OD=OE,
∴∠OED=∠D=70°,
∴∠DOE=180°﹣2×70°=40°,
∴ ( http: / / www.21cnjy.com )的长= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com );
故选:B.
( http: / / www.21cnjy.com )
3.(2017 南宁)如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧 ( http: / / www.21cnjy.com )的长等于( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】连接OB、OC,利用圆周角定理求得∠BOC=60°,然后利用弧长公式l= ( http: / / www.21cnjy.com )来计算劣弧 ( http: / / www.21cnjy.com )的长.
【解答】解:如图,连接OB、OC,
∵∠BAC=30°,
∴∠BOC=2∠BAC=60°,
又OB=OC,
∴△OBC是等边三角形,
∴BC=OB=OC=2,
∴劣弧 ( http: / / www.21cnjy.com )的长为: ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
故选:A.
( http: / / www.21cnjy.com )
4.(2017 马龙县校级一模)一个扇形的圆心角为60°,弧长为2π厘米,则这个扇形的半径为( )【来源:21cnj*y.co*m】
A.6厘米 B.12厘米 C. ( http: / / www.21cnjy.com )厘米 D. ( http: / / www.21cnjy.com )厘米
【分析】代入弧长公式,解出扇形的半径R即可.
【解答】解:l= ( http: / / www.21cnjy.com ),
由题意得,2π= ( http: / / www.21cnjy.com ),
解得:R=6cm.
故选A.
5.(2017 满洲里市模拟)如图,⊙O的半径为1,A、B、C是圆周上的三点,∠BAC=36°,则劣弧BC的长是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】连接OB,OC,依据同弧所对的圆周角等于圆心角的一半,即可求得劣弧BC的圆心角的度数,然后利用弧长计算公式求解即可.21·世纪*教育网
【解答】解:连接OB,OC.
∠BOC=2∠BAC=2×36°=72°,
则劣弧BC的长是: ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )π.
故选B.
( http: / / www.21cnjy.com )
6.(2017 海曙区校级自主招生)如图,正方形ABCD的边AB=1, ( http: / / www.21cnjy.com )和 ( http: / / www.21cnjy.com )都是以1为半径的圆弧,则无阴影两部分的面积之差是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.1﹣ ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com )﹣1 D.1﹣ ( http: / / www.21cnjy.com )
【分析】图中1、2、3、4图形的面积和为正方形的面积,1、2和两个3的面积和是两个扇形的面积,因此两个扇形的面积的和﹣正方形的面积=无阴影两部分的面积之差,即 ( http: / / www.21cnjy.com )﹣1= ( http: / / www.21cnjy.com ).
【解答】解:如图:
正方形的面积=S1+S2+S3+S4;①
两个扇形的面积=2S3+S1+S2;②
②﹣①,得:S3﹣S4=S扇形﹣S正方形= ( http: / / www.21cnjy.com )﹣1= ( http: / / www.21cnjy.com ).
故选:A.
( http: / / www.21cnjy.com )
7.(2017 北京模拟)如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )21*cnjy*com
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.2 ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.1
【分析】首先证明△ABC是等边三角形.则△EDC是等边三角形,边长是2.而 ( http: / / www.21cnjy.com )和弦BE围成的部分的面积= ( http: / / www.21cnjy.com )和弦DE围成的部分的面积.由∠BOE=∠DOE,BE=ED推出S弓BE=S弓DE,这样可以得出S阴=S△EDC,据此即可求解.
【解答】解:连接AE,OD、OE.
∵AB是直径,
∴∠AEB=90°,
又∵∠BED=120°,
∴∠AED=30°,
∴∠AOD=2∠AED=60°.
∵OA=OD
∴△AOD是等边三角形,
∴∠OAD=60°,
∵点E为BC的中点,∠AEB=90°,
∴AB=AC,
∴△ABC是等边三角形,边长是4.△EDC是等边三角形,边长是2.
∴∠BOE=∠EOD=60°,
∴ ( http: / / www.21cnjy.com )和弦BE围成的部分的面积= ( http: / / www.21cnjy.com )和弦DE围成的部分的面积.
∴阴影部分的面积=S△EDC= ( http: / / www.21cnjy.com )×22= ( http: / / www.21cnjy.com ).
故选:A.
( http: / / www.21cnjy.com )
8.(2017 张店区一模)如图,将△ ( http: / / www.21cnjy.com )ABC绕点C按顺时针旋转60°得到△A′B′C,已知AC=6,BC=4,则线段AB扫过的图形的面积为( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com )π B. ( http: / / www.21cnjy.com )π C.6π D. ( http: / / www.21cnjy.com )π
【分析】根据图形可以得出AB扫过的 ( http: / / www.21cnjy.com )图形的面积=S扇形ACA′+S△ABC﹣S扇形BCB′﹣S△A′B′C,由旋转的性质就可以得出S△ABC=S△A′B′C就可以得出AB扫过的图形的面积=S扇形ACA′﹣S扇形BCB′求出其值即可.21·cn·jy·com
【解答】解:∵△ABC绕点C旋转60°得到△A′B′C,
∴△ABC≌△A′B′C,
∴S△ABC=S△A′B′C,∠BCB′=∠ACA′=60°.
∵AB扫过的图形的面积=S扇形ACA′+S△ABC﹣S扇形BCB′﹣S△A′B′C,
∴AB扫过的图形的面积=S扇形ACA′﹣S扇形BCB′,
∴AB扫过的图形的面积= ( http: / / www.21cnjy.com )×π×36﹣ ( http: / / www.21cnjy.com )×π×16= ( http: / / www.21cnjy.com )π.
故选D.
9.(2017 海宁市校级模拟)如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为 ( http: / / www.21cnjy.com )π cm2,则扇形圆心角的度数为( )2·1·c·n·j·y
( http: / / www.21cnjy.com )
A.120° B.140° C.150° D.160°
【分析】根据扇形的面积公式列方程即可得到结论.
【解答】解:∵OB=10cm,AB=20cm,
∴OA=OB+AB=30cm,
设扇形圆心角的度数为α,
∵纸面面积为 ( http: / / www.21cnjy.com )π cm2,
∴ ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )π,
∴α=150°,
故选C.
10.(2017 东河区二模)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】先根据平行线的性质得出∠1=∠2,再由正方形的性质得出∠ABD=45°,由S阴影=S扇形ABD+S扇形ENM即可得出结论.www-2-1-cnjy-com
【解答】解:∵AN∥BM,
∴∠1=∠2.
∵四边形ABCD是正方形,
∴∠ABD=45°,
∴S阴影=S扇形ABD+S扇形ENM= ( http: / / www.21cnjy.com )+ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
故选B.
( http: / / www.21cnjy.com )
二.填空题(每小题5分,共30分)
11.(2017 白银)如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于 ( http: / / www.21cnjy.com ) .(结果保留π)【出处:21教育名师】
( http: / / www.21cnjy.com )
【分析】先根据ACB=90°,AC=1,AB=2,得到∠ABC=30°,进而得出∠A=60°,再根据AC=1,即可得到弧CD的长.
【解答】解:∵∠ACB=90°,AC=1,AB=2,
∴∠ABC=30°,
∴∠A=60°,
又∵AC=1,
∴弧CD的长为 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
故答案为: ( http: / / www.21cnjy.com ).
12.(2017 黔南州)如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则 ( http: / / www.21cnjy.com )的长为 ( http: / / www.21cnjy.com )π .
( http: / / www.21cnjy.com )
【分析】连接OC,如图,利用等腰三角形的性质和三角形内角和可计算出∠AOC=60°,则∠BOC=70°,然后根据弧长公式计算 ( http: / / www.21cnjy.com )的长.21*cnjy*com
【解答】解:连接OC,如图,
∵OA=OC,
∴∠OCA=∠CAO=60°,
∴∠AOC=60°,
∴∠BOC=130°﹣60°=70°,
∴ ( http: / / www.21cnjy.com )的长= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )π.
故答案为 ( http: / / www.21cnjy.com )π.
( http: / / www.21cnjy.com )
13.(2017 聊城)如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中 ( http: / / www.21cnjy.com )的长为 22015π. .
( http: / / www.21cnjy.com )
【分析】连接P1O1,P2O2,P3O3,易求得PnOn垂直于x轴,可得 ( http: / / www.21cnjy.com ) 为 ( http: / / www.21cnjy.com )圆的周长,再找出圆半径的规律即可解题.
【解答】解:连接P1O1,P2O2,P3O3…
( http: / / www.21cnjy.com )
∵P1 是⊙O2上的点,
∴P1O1=OO1,
∵直线l解析式为y=x,
∴∠P1OO1=45°,
∴△P1OO1为等腰直角三角形,即P1O1⊥x轴,
同理,PnOn垂直于x轴,
∴ ( http: / / www.21cnjy.com ) 为 ( http: / / www.21cnjy.com )圆的周长,
∵以O1为圆心,O1O为半径画圆,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交x轴正半轴于点O3,以此类推,
∴OOn=2n﹣1,
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ) 2π OOn= ( http: / / www.21cnjy.com )π 2n﹣1=2n﹣2π,
当n=2017时, ( http: / / www.21cnjy.com )=22015π.
故答案为 22015π.
14.(2017 济南)如图,扇形 ( http: / / www.21cnjy.com )纸叠扇完全打开后,扇形ABC的面积为300πcm2,∠BAC=120°,BD=2AD,则BD的长度为 20 cm.
( http: / / www.21cnjy.com )
【分析】设AD=x,则AB=3x.由题意300π= ( http: / / www.21cnjy.com ),解方程即可.
【解答】解:设AD=x,则AB=3x.
由题意300π= ( http: / / www.21cnjy.com ),
解得x=10,
∴BD=2x=20cm.
故答案为20.
15.(2017 怀化)如图,⊙O的半径为2,点A,B在⊙O上,∠AOB=90°,则阴影部分的面积为 π﹣2 .2-1-c-n-j-y
( http: / / www.21cnjy.com )
【分析】根据∠AOB=90°,OA=OB可知△OAB是等腰直角三角形,根据S阴影=S扇形OAB﹣S△OAB即可得出结论.
【解答】解:∵∠AOB=90°,OA=OB,
∴△OAB是等腰直角三角形.
∵OA=2,
∴S阴影=S扇形OAB﹣S△OAB= ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com )×2×2=π﹣2.
故答案为π﹣2.
16.(2017 铁岭)如图,在圆心角为135°的扇形OAB中,半径OA=2cm,点C,D为 ( http: / / www.21cnjy.com )的三等分点,连接OC,OD,AC,CD,BD,则图中阴影部分的面积为 ( ( http: / / www.21cnjy.com )π﹣3 ( http: / / www.21cnjy.com )) cm2.www.21-cn-jy.com
( http: / / www.21cnjy.com )
【分析】易知△AOC≌△COD≌△DOB,如 ( http: / / www.21cnjy.com )图作DH⊥OB于H.求出DH,即可求出△DOB的面积,再根据阴影部分面积=扇形面积﹣三个三角形面积,计算即可.
【解答】解:如图作DH⊥OB于H.
( http: / / www.21cnjy.com )
∵点C,D为 ( http: / / www.21cnjy.com )的三等分点,∠AOB=135°,
∴∠AOC=∠COD=∠DOB=45°,
∴△ODH是等腰直角三角形,△AOC≌△COD≌△DOB,
∵OD=2,
∴DH=OH= ( http: / / www.21cnjy.com ),
∴S△ODB= ( http: / / www.21cnjy.com ) OB DH= ( http: / / www.21cnjy.com ),
∴S△AOC=S△COD=S△DOB= ( http: / / www.21cnjy.com ),
∴S阴= ( http: / / www.21cnjy.com )﹣3S△DOB=( ( http: / / www.21cnjy.com )π﹣3 ( http: / / www.21cnjy.com ))cm2,
故答案为( ( http: / / www.21cnjy.com )π﹣3 ( http: / / www.21cnjy.com ))cm2.
三.解答题(共20分)
17.(8分)(2017 嵊州市模拟)如图,点A、B、C在圆O上,AB为直径,且AB=4,AC=2.
(1)求∠ABC的度数;
(2)求弧AC的长度.
( http: / / www.21cnjy.com )
【分析】(1)根据圆周角定理得到∠C=90°,求得sin∠B= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),于是得到结论;
(2)根据圆周角定理得到∠AOC=60°,根据弧长公式即可得到结论.
【解答】解:(1)
∵AB为直径,
∴∠C=90°,
∵AB=4,AC=2,
∴sin∠B= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴∠ABC=30°;
(2)连接OC,
∵∠B=30°,
∴∠AOC=60°,
∴弧AC的长度= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )π.
18.(12分)(2016 扬中市一模)已知如图,在直角坐标系xOy中,点A,点B坐标分别为(﹣1,0),(0, ( http: / / www.21cnjy.com )),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
(1)求点C的坐标;
(2)△AOB绕点O顺时针旋转60°所扫过的面积;
(3)线段AB绕点O顺时针旋转60°所扫过的面积.
( http: / / www.21cnjy.com )
【分析】(1)如图1,过C作CE⊥OA于E,由点A,点B坐标分别为(﹣1,0),(0, ( http: / / www.21cnjy.com )),得到OA=1,OB= ( http: / / www.21cnjy.com ),根据旋转的性质得到∠AOC=∠BOD=60°,AO=OC=1,解直角三角形即可得到结论;
(2)根据三角形和扇形的面积公式即可得到结论;
(3)根据三角形和扇形的面积公式即可得到结论;
【解答】解:(1)如图1,过C作CE⊥OA于E,
∵点A,点B坐标分别为(﹣1,0),(0, ( http: / / www.21cnjy.com )),
∴OA=1,OB= ( http: / / www.21cnjy.com ),
∵△AOB绕点O顺时针旋转60°得到△COD,
∴∠AOC=∠BOD=60°,AO=OC=1,
∴OE= ( http: / / www.21cnjy.com )OC= ( http: / / www.21cnjy.com ),CE= ( http: / / www.21cnjy.com )OC= ( http: / / www.21cnjy.com ),
∴C(﹣ ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ));
(2)△AOB绕点O顺时针旋转60°所扫过的面积= ( http: / / www.21cnjy.com )+ ( http: / / www.21cnjy.com )+ ( http: / / www.21cnjy.com )× ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )π+ ( http: / / www.21cnjy.com );
(3)如图2,线段AB绕点O顺时针旋转60°所扫过的面积═( ( http: / / www.21cnjy.com )﹣1× ( http: / / www.21cnjy.com ))+( ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com ))+( ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com ))= ( http: / / www.21cnjy.com )π﹣ ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
