广东省中山市2017—2018学年度高二上学期理科数学期末复习(选修2-2 第一章《导数及其应用》)
文档属性
| 名称 | 广东省中山市2017—2018学年度高二上学期理科数学期末复习(选修2-2 第一章《导数及其应用》) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-29 09:25:26 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
广东省中山市2017—2018学年度高二上学期理科数学期末复习
选修2-2 第一章《导数及其应用》单元测试题
班别 登分号 姓名 成绩
一、选择题
1.函数的导数是( )
A. B.
C. D.
2.函数的一个单调递增区间是( )
A. B. C. D.
3.已知对任意实数,有,且时,,则时( )
A. B.
C. D.
4.若函数在内有极小值,则( )
A. B. C. D.
5.若曲线的一条切线与直线垂直,则的方程为( )
A. B. C. D.
6.曲线在点处的切线与坐标轴所围三角形的面积为( )
A. B. C. D.
7.设是函数的导函数,将和的图象画在同一个直角坐标系中,不可能正确的是( )
( http: / / www.21cnjy.com )
8.已知二次函数的导数为,,对于任意实数都有,则的最小值为( )
A. B. C. D.
9.设在内单调递增,,则是的()
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
10. 函数的图像如图所示,下列数值排序正确的是( )
A. y
B.
C.
D. O 1 2 3 4 x
11. 已知函数在处可导,则等于 ( )
A. B.2 C.-2 D.0
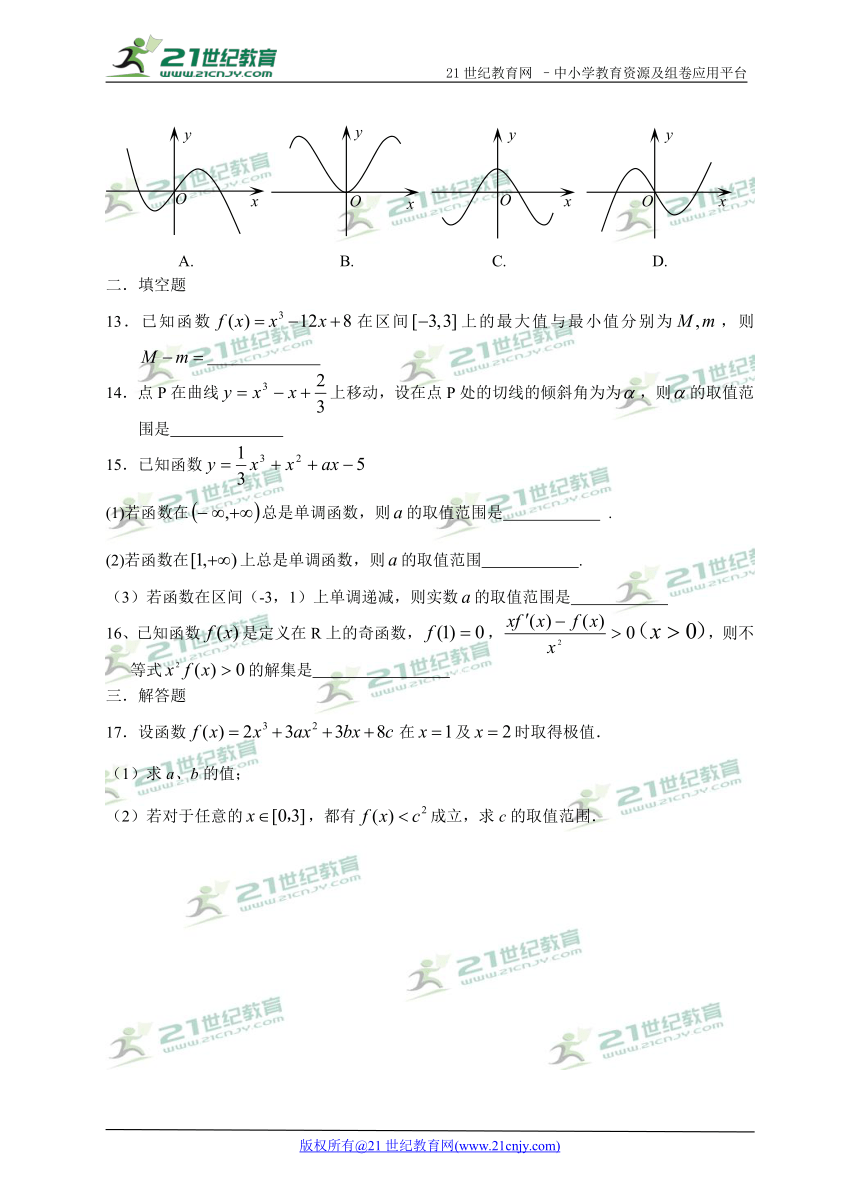
12、设曲线在点处的切线的斜率为,则函数的部分图象可以为
A. B. C. D.
二.填空题
13.已知函数在区间上的最大值与最小值分别为,则
14.点P在曲线上移动,设在点P处的切线的倾斜角为为,则的取值范围是 21教育网
15.已知函数
(1)若函数在总是单调函数,则的取值范围是 .
(2)若函数在上总是单调函数,则的取值范围 .
(3)若函数在区间(-3,1)上单调递减,则实数的取值范围是
16、已知函数 ( http: / / www.21cnjy.com )是定义在R上的奇函数, ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ),则不等式 ( http: / / www.21cnjy.com )的解集是 21世纪教育网版权所有
三.解答题
17.设函数在及时取得极值.
(1)求a、b的值;
(2)若对于任意的,都有成立,求c的取值范围.
18、已知函数
(1)求的单调递减区间;
(2)若在区间[-2,2]上的最大值为20,求它在该区间上的最小值
19. 已知函数
(1)求曲线在点处的切线方程;
(2)若关于的方程有三个不同的实根,求实数的取值范围.
20.已知函数在处取得极值.
(1)讨论和是函数的极大值还是极小值;
(2)过点作曲线的切线,求此切线方程.
21.已知
(1)当时,求函数的单调区间。
(2)当时,讨论函数的单调增区间。
(3)是否存在负实数,使,函数有最小值-3?
22.已知函数,,其中.
(1)若是函数的极值点,求实数的值;
(2)若对任意的(为自然对数的底数)都有≥成立,求实数的取值范围.
选修2-2 第一章《导数及其应用》单元测试题参考答案
一、选择题CABAA DDCBB BA
二、填空 32 (1)
三、解答题
17.解:(1),
因为函数在及取得极值,则有,.
即解得,.
(2)由(Ⅰ)可知,,
.
当时,;
当时,;
当时,.
所以,当时,取得极大值,又,.
则当时,的最大值为.
因为对于任意的,有恒成立,所以 ,解得 或,
因此的取值范围为.
18解:(1)
令
所以函数的单调递减区间为(-,-1)和(3,+)
(2)因为
所以
因为在(-1,3)上>0,所以在[-1,2]上单调递增,
又由于在[-2,-1]上单调递减,
因此f(2)和f(-1)分别是在区间[-2,2]上的最大值和最小值
于是有22+a=20,解得a=-2。故
因此f(-1)=1+3-9-2=-7,即函数在区间[-2,2]上的最小值为-7。
19解(1) ………………………2分
∴曲线在处的切线方程为,即;……4分
(2)记
令或1. …………………………………………………………6分
则的变化情况如下表
极大 极小
当有极大值有极小值. ………………………10分
由的简图知,当且仅当即时,
函数有三个不同零点,过点可作三条不同切线.
所以若过点可作曲线的三条不同切线,的范围是.…………14分
20解:(1),依题意,
,即 解得 ┅┅ (3分)
∴,∴
令,得
若,则, 故在上是增函数;
若,则, 故在上是减函数;
所以是极大值,是极小值。 ┅┅┅┅┅┅┅┅ (6分)
(2) 设切点为,则
由知,切线方程为
┅┅┅┅┅┅┅┅┅┅ (9分)
又点在切线上,有
化简得 ,解得
所以切点为,切线方程为 ┅┅┅┅┅┅ (12分)
19.(1)递减区间和;递增区间
(2)当递增区间
当递增区间
当递增区间和
当递增区间
当递增区间和
(3)当 递增,,解得
当由单调性知:,化简得:,解得
,不合要求;
综上,为所求。
22.(1)解:∵,其定义域为, ∴.
∵是函数的极值点,∴,即.
∵,∴. 经检验当时,是函数的极值点,∴.
(2)解:对任意的都有≥成立等价于对任意的都有≥.
当[1,]时,.∴函数在上是增函数.
∴.
∵,且,.
①当且[1,]时,,
∴函数在[1,]上是增函数,∴.
由≥,得≥,又,∴不合题意.
②当1≤≤时,
若1≤<,则,
若<≤,则.
∴函数在上是减函数,在上是增函数.
∴.
由≥,得≥,又1≤≤,∴≤≤.
③当且[1,]时,,
∴函数在上是减函数.∴.
由≥,得≥,又,∴.
综上所述,的取值范围为.
教育网
( http: / / www.21cnjy.com )
O
x
x
x
x
y
y
y
y
O
O
O
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
广东省中山市2017—2018学年度高二上学期理科数学期末复习
选修2-2 第一章《导数及其应用》单元测试题
班别 登分号 姓名 成绩
一、选择题
1.函数的导数是( )
A. B.
C. D.
2.函数的一个单调递增区间是( )
A. B. C. D.
3.已知对任意实数,有,且时,,则时( )
A. B.
C. D.
4.若函数在内有极小值,则( )
A. B. C. D.
5.若曲线的一条切线与直线垂直,则的方程为( )
A. B. C. D.
6.曲线在点处的切线与坐标轴所围三角形的面积为( )
A. B. C. D.
7.设是函数的导函数,将和的图象画在同一个直角坐标系中,不可能正确的是( )
( http: / / www.21cnjy.com )
8.已知二次函数的导数为,,对于任意实数都有,则的最小值为( )
A. B. C. D.
9.设在内单调递增,,则是的()
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
10. 函数的图像如图所示,下列数值排序正确的是( )
A. y
B.
C.
D. O 1 2 3 4 x
11. 已知函数在处可导,则等于 ( )
A. B.2 C.-2 D.0
12、设曲线在点处的切线的斜率为,则函数的部分图象可以为
A. B. C. D.
二.填空题
13.已知函数在区间上的最大值与最小值分别为,则
14.点P在曲线上移动,设在点P处的切线的倾斜角为为,则的取值范围是 21教育网
15.已知函数
(1)若函数在总是单调函数,则的取值范围是 .
(2)若函数在上总是单调函数,则的取值范围 .
(3)若函数在区间(-3,1)上单调递减,则实数的取值范围是
16、已知函数 ( http: / / www.21cnjy.com )是定义在R上的奇函数, ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ),则不等式 ( http: / / www.21cnjy.com )的解集是 21世纪教育网版权所有
三.解答题
17.设函数在及时取得极值.
(1)求a、b的值;
(2)若对于任意的,都有成立,求c的取值范围.
18、已知函数
(1)求的单调递减区间;
(2)若在区间[-2,2]上的最大值为20,求它在该区间上的最小值
19. 已知函数
(1)求曲线在点处的切线方程;
(2)若关于的方程有三个不同的实根,求实数的取值范围.
20.已知函数在处取得极值.
(1)讨论和是函数的极大值还是极小值;
(2)过点作曲线的切线,求此切线方程.
21.已知
(1)当时,求函数的单调区间。
(2)当时,讨论函数的单调增区间。
(3)是否存在负实数,使,函数有最小值-3?
22.已知函数,,其中.
(1)若是函数的极值点,求实数的值;
(2)若对任意的(为自然对数的底数)都有≥成立,求实数的取值范围.
选修2-2 第一章《导数及其应用》单元测试题参考答案
一、选择题CABAA DDCBB BA
二、填空 32 (1)
三、解答题
17.解:(1),
因为函数在及取得极值,则有,.
即解得,.
(2)由(Ⅰ)可知,,
.
当时,;
当时,;
当时,.
所以,当时,取得极大值,又,.
则当时,的最大值为.
因为对于任意的,有恒成立,所以 ,解得 或,
因此的取值范围为.
18解:(1)
令
所以函数的单调递减区间为(-,-1)和(3,+)
(2)因为
所以
因为在(-1,3)上>0,所以在[-1,2]上单调递增,
又由于在[-2,-1]上单调递减,
因此f(2)和f(-1)分别是在区间[-2,2]上的最大值和最小值
于是有22+a=20,解得a=-2。故
因此f(-1)=1+3-9-2=-7,即函数在区间[-2,2]上的最小值为-7。
19解(1) ………………………2分
∴曲线在处的切线方程为,即;……4分
(2)记
令或1. …………………………………………………………6分
则的变化情况如下表
极大 极小
当有极大值有极小值. ………………………10分
由的简图知,当且仅当即时,
函数有三个不同零点,过点可作三条不同切线.
所以若过点可作曲线的三条不同切线,的范围是.…………14分
20解:(1),依题意,
,即 解得 ┅┅ (3分)
∴,∴
令,得
若,则, 故在上是增函数;
若,则, 故在上是减函数;
所以是极大值,是极小值。 ┅┅┅┅┅┅┅┅ (6分)
(2) 设切点为,则
由知,切线方程为
┅┅┅┅┅┅┅┅┅┅ (9分)
又点在切线上,有
化简得 ,解得
所以切点为,切线方程为 ┅┅┅┅┅┅ (12分)
19.(1)递减区间和;递增区间
(2)当递增区间
当递增区间
当递增区间和
当递增区间
当递增区间和
(3)当 递增,,解得
当由单调性知:,化简得:,解得
,不合要求;
综上,为所求。
22.(1)解:∵,其定义域为, ∴.
∵是函数的极值点,∴,即.
∵,∴. 经检验当时,是函数的极值点,∴.
(2)解:对任意的都有≥成立等价于对任意的都有≥.
当[1,]时,.∴函数在上是增函数.
∴.
∵,且,.
①当且[1,]时,,
∴函数在[1,]上是增函数,∴.
由≥,得≥,又,∴不合题意.
②当1≤≤时,
若1≤<,则,
若<≤,则.
∴函数在上是减函数,在上是增函数.
∴.
由≥,得≥,又1≤≤,∴≤≤.
③当且[1,]时,,
∴函数在上是减函数.∴.
由≥,得≥,又,∴.
综上所述,的取值范围为.
教育网
( http: / / www.21cnjy.com )
O
x
x
x
x
y
y
y
y
O
O
O
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
