广东省中山市2017—2018学年度高二上学期理科数学期末复习(选修2-1 第三章 空间向量与立体几何)
文档属性
| 名称 | 广东省中山市2017—2018学年度高二上学期理科数学期末复习(选修2-1 第三章 空间向量与立体几何) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-29 09:08:54 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
广东省中山市2017—2018学年度高二上学期理科数学期末复习
选修2-1 《第三章 空间向量与立体几何》单元测试题
一、选择题(本大题共10个小题,每小题5分,共50分.)
1. 若, , 则( )
A. 4 B. 15 C. 7 D. 3
2.下列等式中,使点M与点A、B、C一定共面的是( )
A. B.
C. D.
3.若 则是的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
4.在平行六面体ABCD—A1B1C1D1中,M为AC与BD的交点.若=a,
=b,=c,则下列向量中与相等的向量是( )
A.-a+b+c B.a+b+c
C.a-b+c D.-a-b+c
5.在棱长为1的正四面体ABCD中,E, F分别是 BC, AD的中点,则( )
A. 0 B. C. D.
6.如图,在平行六面体中,底面是边长为1的正
方形,若,且,则的长为( )
A. B. C. D.
7.已知下列命题: ① 若A、B、C、D是空间任意四点,则有+++=;
② 是、共线的充要条件;③ 若是空间三向量,则;④ 对空间任意点O与不共线的三点A、B、C,若=x+y+z(其中x、y、z∈R),则P、A、B、C四点共面,其中不正确的是( )21世纪教育网版权所有
A.①② B.②③ C.③④ D.②④
8.在长方体A—C1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为( )
A. B. C. D.
9.在棱长为2的正方体中,正方形所在平面内的动点到直线
的距离之和为,若,则点P到直线 的距离为( )
A. B. C. D.
10.如图,正三棱锥P-ABC的底面边长 ( http: / / www.21cnjy.com )为1,E,F,G,H,分别是PA,AC,BC,PD的中点,四边形EFGH的面积为S(x),则S(x)值域为_________21教育网
A. {} B.(0, +∞)
C .(, +∞) D.(, +∞)
二、填空题(本大题共4小题,每小题5分,共20分)
11. 已知=(—4,2,x),=(2,1,3),且⊥,则x= 。
12. 向量 ,,则和所夹角是
13. 已知A(1, 0, 0), B(0, 1, 0 ), C(0, 0, 1), 点D满足条件:DB⊥AC, DC⊥AB,
AD=BC, 则D的坐标为
14.如图,P—ABCD是正四棱锥,是正方体,其中, ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
则到平面PAD的距离为 .
三、解答题
15.如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PA的长为2,且PA与AB、AD的夹角都等于600,是PC的中点,设.
(1)试用表示出向量;(2)求的长.
16.如图,在长方体中,,点E、F分别是面、面的中心.以D为坐标原点,DA、DC、DD1所为直线为x,y,z轴建立空间直角坐标系,试用向量方法解决下列问题:21cnjy.com
(1)求异面直线和所成的角;
(2)求直线和平面所成角的正弦值.
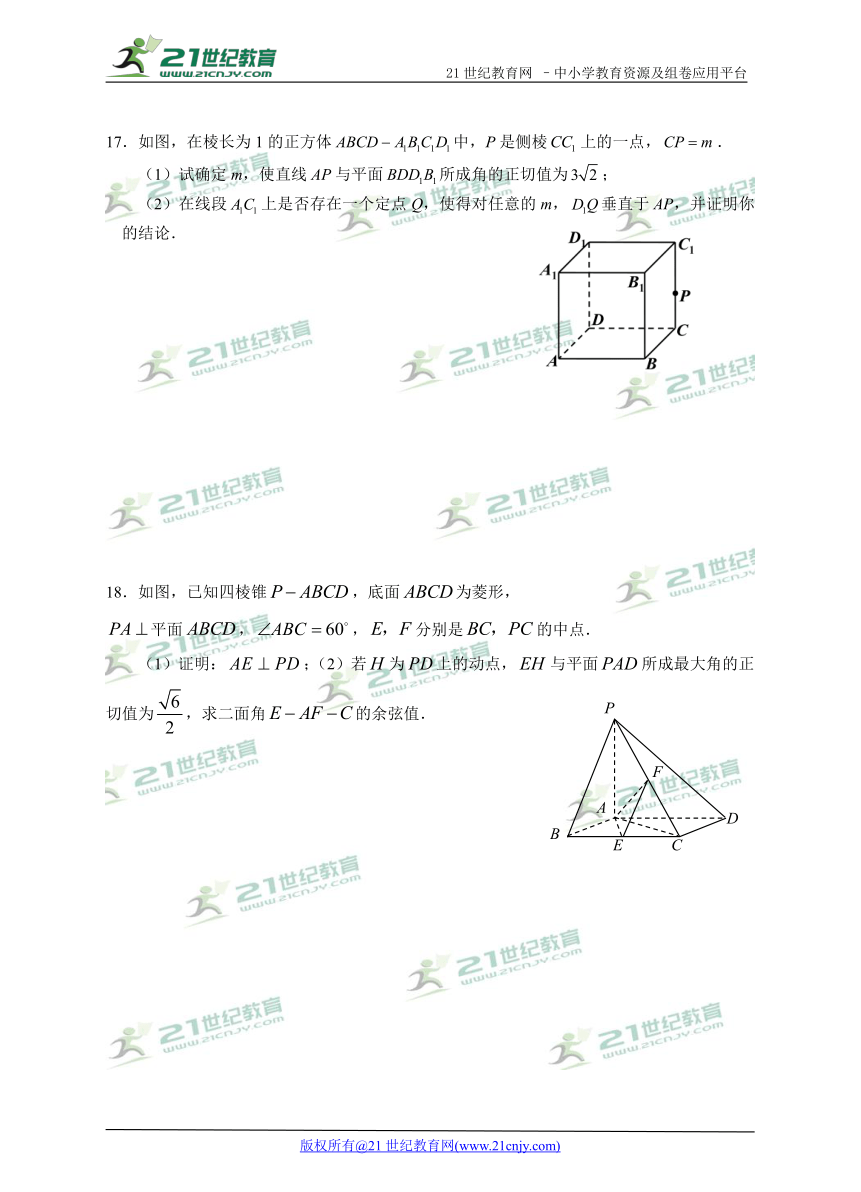
17.如图,在棱长为1的正方体中,P是侧棱上的一点,.
(1)试确定m,使直线AP与平面所成角的正切值为;
(2)在线段上是否存在一个定点Q,使得对任意的m,垂直于AP,并证明你的结论.
18.如图,已知四棱锥,底面为菱形,
平面,,分别是的中点.
(1)证明:;(2)若为上的动点,与平面所成最大角的正切值为,求二面角的余弦值.
选修2-1 《第三章 空间向量与立体几何》单元测试题参考答案
一、选择题
1.D 2.D 3.A 4.A 5.D 6.A 7.D 8.D 9.A 10.C
二、填空题
11. 2 12.60° 13.(1,1,1)或 14.
三、答题
15.解:(1)∵是PC的中点,∴
(2)
.
16. 解:(1)A(2,0,0),F(1,2,),
B(2,2,0),E(1,1,),C(0,2,0).
∴ , ……(4分)
∴ . ……(6分)
所以AF和BE所成的角为 . ……(7分)
(2)设平面BEC的一个法向量为
又
则:,.
∴, 令,则:,∴ . …………(10分)
∴ . ……………(12分)
设直线和平面所成角为,则:.
即 直线和平面所成角的正弦值为. ……………(14分)
17.解:(1)建立如图所示的空间直角坐标系,……1分
( http: / / www.21cnjy.com )
则A(1,0,0), B(1,1,0), P(0,1,m),C(0,1,0), D(0,0,0), B1(1,1,1), D1(0,0,1).
所以 ……2分
又由的一个法向量. ……3分
设与所成的角为,
则 ……4分
依题意有:,解得. ……5分
故当时,直线. ……6分
(2)若在上存在这样的点,设此点的横坐标为,……7分
则. ……8分
依题意,对任意的要使,只需对任意m恒成立 ……9分
,……11分
即Q为的中点时,满足题设的要求 ……12分
18.(1)证明:由四边形为菱形,,可得为正三角形.
因为为的中点,所以.
又,因此.
因为平面,平面,所以.
而平面,平面且,
所以平面.又平面,
所以.
(2)解:
由(1)知两两垂直,以为坐标原点,建立如图所示的空间直角坐标系,又分别为的中点,所以
,
,
所以.
设平面的一法向量为,
则因此
取,则,
因为,,,所以平面,
故为平面的一法向量.
又,所以.
因为二面角为锐角,所以所求二面角的余弦值为.
选修2-1 《第三章 空间向量与立体几何》单元测试题参考答案及部分解析
一、选择题
1.D 2.D 3.A 4.A 5.D 6.A 7.D 8.D 9.A 10.C
1.=c+(-a+b)=-a+b+c,故选A.
2.解:设以为基底,则
所以。选A.
3.解:设, 易知。即条件具有充分性。
又若时,,虽有,但条件显然不成立,所以条件不具有必然性。
4.解:=
=
==。选D.
5.
故选D.
10.解:当顶点P与底面正⊿ABC重心很接近时,矩形EFGH的面积较小;重合时矩形的面积为选C.
二、填空题
13. 2 14.60° 15.(1,1,1)或 16.
11.解:由, ,
有,,
解得,, .
13解:设D(x, y, z), 则,(x-1, y, z),
(-1, 0, 1), (-1,1, 0), (0, -1, 1). 又DB⊥AC-x+z=0,
DC⊥AB-x+y=0, AD=BC
联立解得x=y=z=1或x=y=z=所以D点为(1,1,1)或。
14.以为轴,为轴,为轴建立空间直角坐标系
设平面PAD的法向量是,
,∴,取得,
,∴到平面PAD的距离.
三、答题
15.解:(1)∵是PC的中点,∴
(2)
.
16. 解:(1)A(2,0,0),F(1,2,),
B(2,2,0),E(1,1,),C(0,2,0).
∴ , ……(4分)
∴ . ……(6分)
所以AF和BE所成的角为 . ……(7分)
(2)设平面BEC的一个法向量为
又
则:,.
∴, 令,则:,∴ . …………(10分)
∴ . ……………(12分)
设直线和平面所成角为,则:.
即 直线和平面所成角的正弦值为. ……………(14分)
17.解:(1)建立如图所示的空间直角坐标系,……1分
( http: / / www.21cnjy.com )
则A(1,0,0), B(1,1,0), P(0,1,m),C(0,1,0), D(0,0,0), B1(1,1,1), D1(0,0,1).
所以 ……2分
又由的一个法向量. ……3分
设与所成的角为,
则 ……4分
依题意有:,解得. ……5分
故当时,直线. ……6分
(2)若在上存在这样的点,设此点的横坐标为,……7分
则. ……8分
依题意,对任意的要使,只需对任意m恒成立 ……9分
,……11分
即Q为的中点时,满足题设的要求 ……12分
18.(1)证明:由四边形为菱形,,可得为正三角形.
因为为的中点,所以.
又,因此.
因为平面,平面,所以.
而平面,平面且,
所以平面.又平面,
所以.
(2)解:
由(1)知两两垂直,以为坐标原点,建立如图所示的空间直角坐标系,又分别为的中点,所以
,
,
所以.
设平面的一法向量为,
则因此
取,则,
因为,,,所以平面,
故为平面的一法向量.
又,所以.
因为二面角为锐角,所以所求二面角的余弦值为.
( http: / / www.21cnjy.com )
A
A1
B
C
D
B1
C1
D1
E
F
P
B
E
C
D
F
A
A
A1
B
C
D
B1
C1
D1
E
F
P
B
E
C
D
F
A
y
z
x
A
A1
B
C
D
B1
C1
D1
E
F
P
B
E
C
D
F
A
y
z
x
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
广东省中山市2017—2018学年度高二上学期理科数学期末复习
选修2-1 《第三章 空间向量与立体几何》单元测试题
一、选择题(本大题共10个小题,每小题5分,共50分.)
1. 若, , 则( )
A. 4 B. 15 C. 7 D. 3
2.下列等式中,使点M与点A、B、C一定共面的是( )
A. B.
C. D.
3.若 则是的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
4.在平行六面体ABCD—A1B1C1D1中,M为AC与BD的交点.若=a,
=b,=c,则下列向量中与相等的向量是( )
A.-a+b+c B.a+b+c
C.a-b+c D.-a-b+c
5.在棱长为1的正四面体ABCD中,E, F分别是 BC, AD的中点,则( )
A. 0 B. C. D.
6.如图,在平行六面体中,底面是边长为1的正
方形,若,且,则的长为( )
A. B. C. D.
7.已知下列命题: ① 若A、B、C、D是空间任意四点,则有+++=;
② 是、共线的充要条件;③ 若是空间三向量,则;④ 对空间任意点O与不共线的三点A、B、C,若=x+y+z(其中x、y、z∈R),则P、A、B、C四点共面,其中不正确的是( )21世纪教育网版权所有
A.①② B.②③ C.③④ D.②④
8.在长方体A—C1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为( )
A. B. C. D.
9.在棱长为2的正方体中,正方形所在平面内的动点到直线
的距离之和为,若,则点P到直线 的距离为( )
A. B. C. D.
10.如图,正三棱锥P-ABC的底面边长 ( http: / / www.21cnjy.com )为1,E,F,G,H,分别是PA,AC,BC,PD的中点,四边形EFGH的面积为S(x),则S(x)值域为_________21教育网
A. {} B.(0, +∞)
C .(, +∞) D.(, +∞)
二、填空题(本大题共4小题,每小题5分,共20分)
11. 已知=(—4,2,x),=(2,1,3),且⊥,则x= 。
12. 向量 ,,则和所夹角是
13. 已知A(1, 0, 0), B(0, 1, 0 ), C(0, 0, 1), 点D满足条件:DB⊥AC, DC⊥AB,
AD=BC, 则D的坐标为
14.如图,P—ABCD是正四棱锥,是正方体,其中, ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
则到平面PAD的距离为 .
三、解答题
15.如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PA的长为2,且PA与AB、AD的夹角都等于600,是PC的中点,设.
(1)试用表示出向量;(2)求的长.
16.如图,在长方体中,,点E、F分别是面、面的中心.以D为坐标原点,DA、DC、DD1所为直线为x,y,z轴建立空间直角坐标系,试用向量方法解决下列问题:21cnjy.com
(1)求异面直线和所成的角;
(2)求直线和平面所成角的正弦值.
17.如图,在棱长为1的正方体中,P是侧棱上的一点,.
(1)试确定m,使直线AP与平面所成角的正切值为;
(2)在线段上是否存在一个定点Q,使得对任意的m,垂直于AP,并证明你的结论.
18.如图,已知四棱锥,底面为菱形,
平面,,分别是的中点.
(1)证明:;(2)若为上的动点,与平面所成最大角的正切值为,求二面角的余弦值.
选修2-1 《第三章 空间向量与立体几何》单元测试题参考答案
一、选择题
1.D 2.D 3.A 4.A 5.D 6.A 7.D 8.D 9.A 10.C
二、填空题
11. 2 12.60° 13.(1,1,1)或 14.
三、答题
15.解:(1)∵是PC的中点,∴
(2)
.
16. 解:(1)A(2,0,0),F(1,2,),
B(2,2,0),E(1,1,),C(0,2,0).
∴ , ……(4分)
∴ . ……(6分)
所以AF和BE所成的角为 . ……(7分)
(2)设平面BEC的一个法向量为
又
则:,.
∴, 令,则:,∴ . …………(10分)
∴ . ……………(12分)
设直线和平面所成角为,则:.
即 直线和平面所成角的正弦值为. ……………(14分)
17.解:(1)建立如图所示的空间直角坐标系,……1分
( http: / / www.21cnjy.com )
则A(1,0,0), B(1,1,0), P(0,1,m),C(0,1,0), D(0,0,0), B1(1,1,1), D1(0,0,1).
所以 ……2分
又由的一个法向量. ……3分
设与所成的角为,
则 ……4分
依题意有:,解得. ……5分
故当时,直线. ……6分
(2)若在上存在这样的点,设此点的横坐标为,……7分
则. ……8分
依题意,对任意的要使,只需对任意m恒成立 ……9分
,……11分
即Q为的中点时,满足题设的要求 ……12分
18.(1)证明:由四边形为菱形,,可得为正三角形.
因为为的中点,所以.
又,因此.
因为平面,平面,所以.
而平面,平面且,
所以平面.又平面,
所以.
(2)解:
由(1)知两两垂直,以为坐标原点,建立如图所示的空间直角坐标系,又分别为的中点,所以
,
,
所以.
设平面的一法向量为,
则因此
取,则,
因为,,,所以平面,
故为平面的一法向量.
又,所以.
因为二面角为锐角,所以所求二面角的余弦值为.
选修2-1 《第三章 空间向量与立体几何》单元测试题参考答案及部分解析
一、选择题
1.D 2.D 3.A 4.A 5.D 6.A 7.D 8.D 9.A 10.C
1.=c+(-a+b)=-a+b+c,故选A.
2.解:设以为基底,则
所以。选A.
3.解:设, 易知。即条件具有充分性。
又若时,,虽有,但条件显然不成立,所以条件不具有必然性。
4.解:=
=
==。选D.
5.
故选D.
10.解:当顶点P与底面正⊿ABC重心很接近时,矩形EFGH的面积较小;重合时矩形的面积为选C.
二、填空题
13. 2 14.60° 15.(1,1,1)或 16.
11.解:由, ,
有,,
解得,, .
13解:设D(x, y, z), 则,(x-1, y, z),
(-1, 0, 1), (-1,1, 0), (0, -1, 1). 又DB⊥AC-x+z=0,
DC⊥AB-x+y=0, AD=BC
联立解得x=y=z=1或x=y=z=所以D点为(1,1,1)或。
14.以为轴,为轴,为轴建立空间直角坐标系
设平面PAD的法向量是,
,∴,取得,
,∴到平面PAD的距离.
三、答题
15.解:(1)∵是PC的中点,∴
(2)
.
16. 解:(1)A(2,0,0),F(1,2,),
B(2,2,0),E(1,1,),C(0,2,0).
∴ , ……(4分)
∴ . ……(6分)
所以AF和BE所成的角为 . ……(7分)
(2)设平面BEC的一个法向量为
又
则:,.
∴, 令,则:,∴ . …………(10分)
∴ . ……………(12分)
设直线和平面所成角为,则:.
即 直线和平面所成角的正弦值为. ……………(14分)
17.解:(1)建立如图所示的空间直角坐标系,……1分
( http: / / www.21cnjy.com )
则A(1,0,0), B(1,1,0), P(0,1,m),C(0,1,0), D(0,0,0), B1(1,1,1), D1(0,0,1).
所以 ……2分
又由的一个法向量. ……3分
设与所成的角为,
则 ……4分
依题意有:,解得. ……5分
故当时,直线. ……6分
(2)若在上存在这样的点,设此点的横坐标为,……7分
则. ……8分
依题意,对任意的要使,只需对任意m恒成立 ……9分
,……11分
即Q为的中点时,满足题设的要求 ……12分
18.(1)证明:由四边形为菱形,,可得为正三角形.
因为为的中点,所以.
又,因此.
因为平面,平面,所以.
而平面,平面且,
所以平面.又平面,
所以.
(2)解:
由(1)知两两垂直,以为坐标原点,建立如图所示的空间直角坐标系,又分别为的中点,所以
,
,
所以.
设平面的一法向量为,
则因此
取,则,
因为,,,所以平面,
故为平面的一法向量.
又,所以.
因为二面角为锐角,所以所求二面角的余弦值为.
( http: / / www.21cnjy.com )
A
A1
B
C
D
B1
C1
D1
E
F
P
B
E
C
D
F
A
A
A1
B
C
D
B1
C1
D1
E
F
P
B
E
C
D
F
A
y
z
x
A
A1
B
C
D
B1
C1
D1
E
F
P
B
E
C
D
F
A
y
z
x
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
