6.2.2平行四边形的判定(2)课件(16张PPT)
文档属性
| 名称 | 6.2.2平行四边形的判定(2)课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-29 00:00:00 | ||
图片预览



文档简介
课件16张PPT。第6章 平行四边形
6.2 平行四边形的判定(2)大家还记得上节课学习的内容吗?判定定理2 两组对边分别相等的四边形是平行四边形判定定理1 一组对边平行且相等的四边形是平行四边形平行线的判定定理1.掌握用对角线互相平分来判定平行四边形的方法;
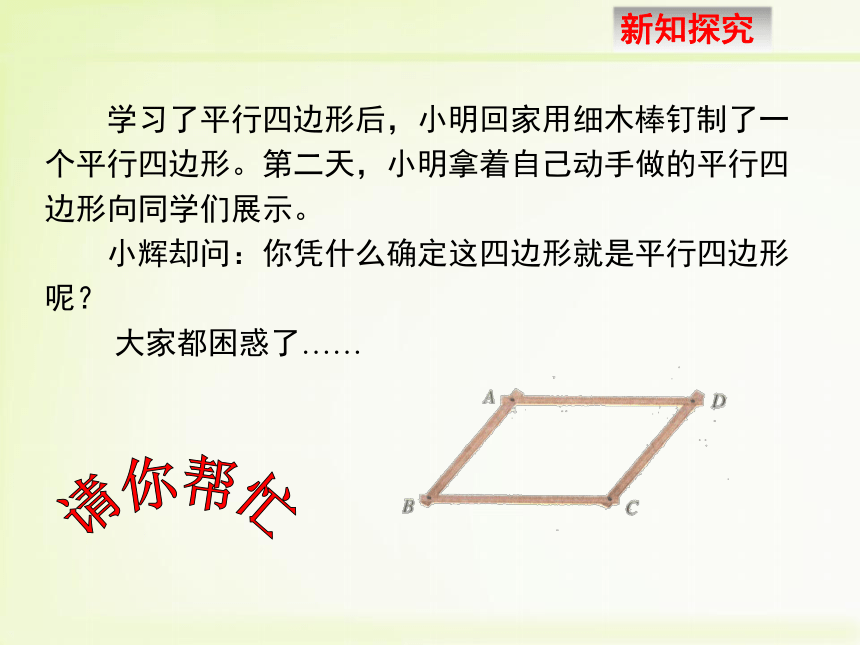
2.会综合运用平行四边形的四种判定方法和性质来证明问题. 学习了平行四边形后,小明回家用细木棒钉制了一个平行四边形。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
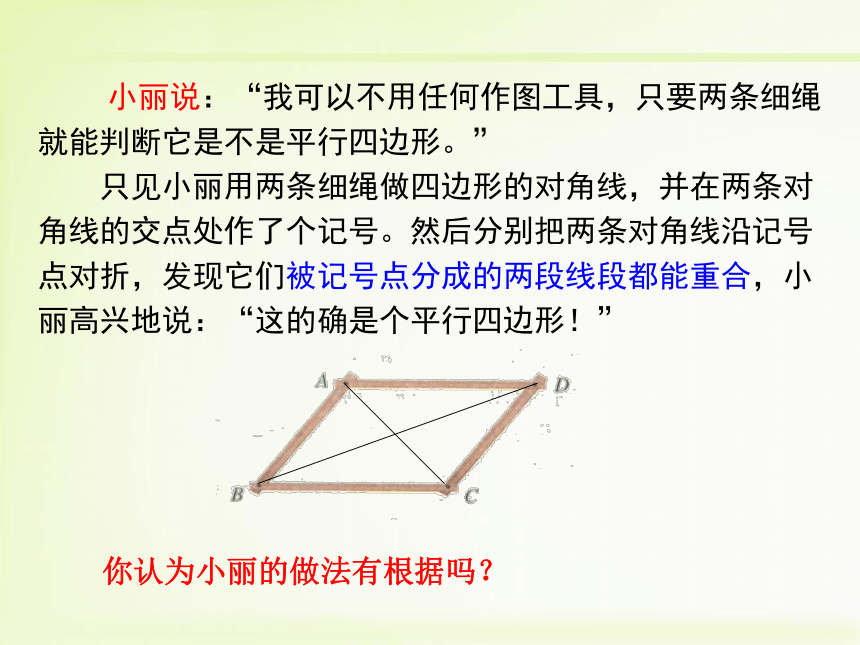
大家都困惑了……请你帮忙 小丽说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
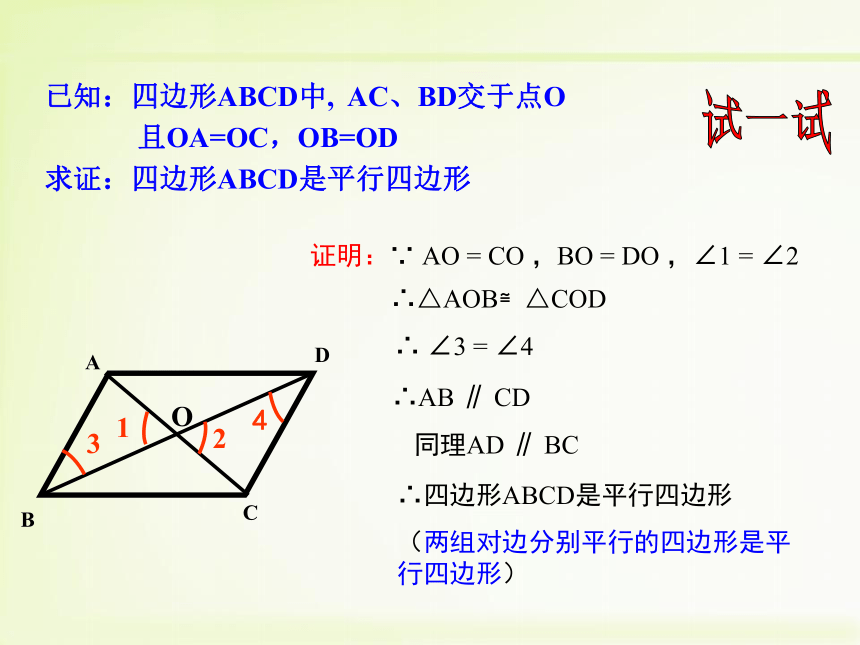
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”你认为小丽的做法有根据吗?已知:四边形ABCD中, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形试一试证明:∵ AO = CO ,BO = DO ,∠1 = ∠2∴△AOB≌△COD∴AB ∥ CD 同理AD ∥ BC∴四边形ABCD是平行四边形
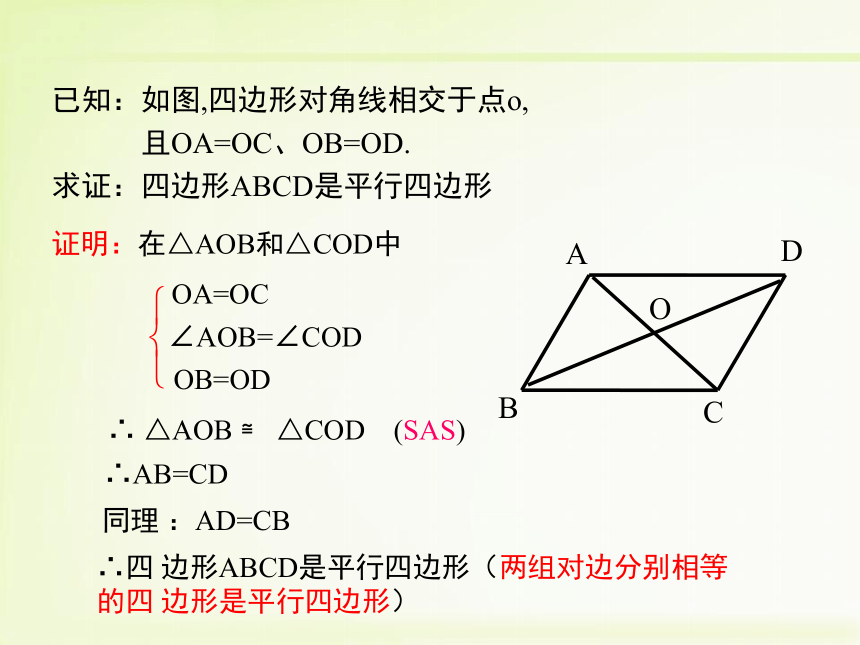
(两组对边分别平行的四边形是平行四边形)∴ ∠3 = ∠4已知:如图,四边形对角线相交于点o,
且OA=OC、OB=OD.
求证:四边形ABCD是平行四边形证明:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 :AD=CB∴四 边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形) 平行四边形的判定平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形. ∵ OA=OC,OB=OD(已知)
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形) ∠A+ ∠B=180 ° AD∥BC 小林提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形。已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形∠A+ ∠D=180 ° AB∥CD∠A+ ∠B +∠C+ ∠D =360 °∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360°
∴ 2∠A+ 2∠B=360°证明:即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)同理可证AB∥CD
∴四边形ABCD是平行四边形已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形平行四边形的判定平行四边形的判定(推论):
两组对角分别相等的四边形是平行四边形. ∵ ∠A=∠C,∠B=∠D (已知)
∴四边形ABCD是平行四边形
(两组对角分别相等的四边形是平行四边形) (1)根据定义:两组对边分别平行的四边形叫做平行四边形。
(2)判定定理1:一组对边平行且相等的四边形是平行四边形。
(3)判定定理2:两组对边分别相等的四边形是平行四边形。
(4)判定定理3:两条对角线互相平分的四边形是平行四边形。
(5)推论:两组对角分别相等的四边形是平行四边形。平行四边形的判别方法例2. 已知:E、F是平行四边形ABCD对角线AC上的两点,并且CE=AF.
求证:四边形BFDE是平行四边形DOABCEF证明:作对角线BD,交AC于点O.
∵四边形ABCD是平行四边形
∴ BO=DO , AO=CO
∵ CE=AF
∴EO=FO
∴ 四边形BFDE是平行四边形(判定定理3) 1. 请你识别下列四边形哪些是平行四边形 ?
请说明理由?⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝ 2. 如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF. 求证:四边形ADEF是平行四边形.思路: 先证明 ΔABC≌ΔFEC(SAS)
再证ΔBDE≌EFC(SAS)习题6.2,第3、5题.结束(1)根据定义:两组对边分别平行的四边形叫做平行四边形。
(2)判定定理1:一组对边平行且相等的四边形是平行四边形。
(3)判定定理2:两组对边分别相等的四边形是平行四边形。
(4)判定定理3:两条对角线互相平分的四边形是平行四边形。
(5)推论:两组对角分别相等的四边形是平行四边形。平行四边形的判别方法有哪些呢?
6.2 平行四边形的判定(2)大家还记得上节课学习的内容吗?判定定理2 两组对边分别相等的四边形是平行四边形判定定理1 一组对边平行且相等的四边形是平行四边形平行线的判定定理1.掌握用对角线互相平分来判定平行四边形的方法;
2.会综合运用平行四边形的四种判定方法和性质来证明问题. 学习了平行四边形后,小明回家用细木棒钉制了一个平行四边形。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……请你帮忙 小丽说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”你认为小丽的做法有根据吗?已知:四边形ABCD中, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形试一试证明:∵ AO = CO ,BO = DO ,∠1 = ∠2∴△AOB≌△COD∴AB ∥ CD 同理AD ∥ BC∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)∴ ∠3 = ∠4已知:如图,四边形对角线相交于点o,
且OA=OC、OB=OD.
求证:四边形ABCD是平行四边形证明:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 :AD=CB∴四 边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形) 平行四边形的判定平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形. ∵ OA=OC,OB=OD(已知)
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形) ∠A+ ∠B=180 ° AD∥BC 小林提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形。已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形∠A+ ∠D=180 ° AB∥CD∠A+ ∠B +∠C+ ∠D =360 °∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360°
∴ 2∠A+ 2∠B=360°证明:即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)同理可证AB∥CD
∴四边形ABCD是平行四边形已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形平行四边形的判定平行四边形的判定(推论):
两组对角分别相等的四边形是平行四边形. ∵ ∠A=∠C,∠B=∠D (已知)
∴四边形ABCD是平行四边形
(两组对角分别相等的四边形是平行四边形) (1)根据定义:两组对边分别平行的四边形叫做平行四边形。
(2)判定定理1:一组对边平行且相等的四边形是平行四边形。
(3)判定定理2:两组对边分别相等的四边形是平行四边形。
(4)判定定理3:两条对角线互相平分的四边形是平行四边形。
(5)推论:两组对角分别相等的四边形是平行四边形。平行四边形的判别方法例2. 已知:E、F是平行四边形ABCD对角线AC上的两点,并且CE=AF.
求证:四边形BFDE是平行四边形DOABCEF证明:作对角线BD,交AC于点O.
∵四边形ABCD是平行四边形
∴ BO=DO , AO=CO
∵ CE=AF
∴EO=FO
∴ 四边形BFDE是平行四边形(判定定理3) 1. 请你识别下列四边形哪些是平行四边形 ?
请说明理由?⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝ 2. 如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF. 求证:四边形ADEF是平行四边形.思路: 先证明 ΔABC≌ΔFEC(SAS)
再证ΔBDE≌EFC(SAS)习题6.2,第3、5题.结束(1)根据定义:两组对边分别平行的四边形叫做平行四边形。
(2)判定定理1:一组对边平行且相等的四边形是平行四边形。
(3)判定定理2:两组对边分别相等的四边形是平行四边形。
(4)判定定理3:两条对角线互相平分的四边形是平行四边形。
(5)推论:两组对角分别相等的四边形是平行四边形。平行四边形的判别方法有哪些呢?
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
