22.1.1二次函数 教案
图片预览


文档简介
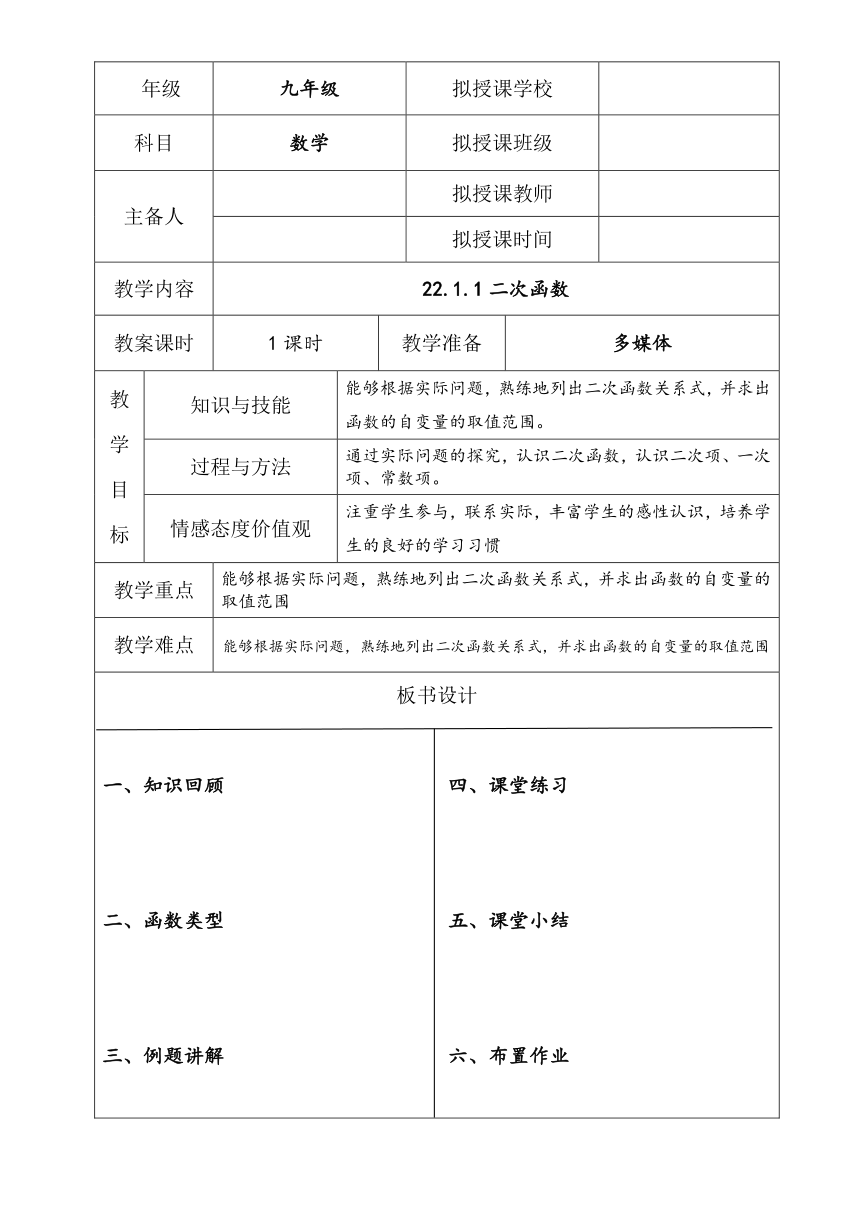
年级 九年级 拟授课学校
科目 数学 拟授课班级
主备人 拟授课教师
拟授课时间
教学内容 22.1.1二次函数
教案课时 1课时 教学准备 多媒体
教学目标 知识与技能 能够根据实际问题,熟练地列出二次函数关系式,并求出函数的自变量的取值范围。
过程与方法 通过实际问题的探究,认识二次函数,认识二次项、一次项、常数项。
情感态度价值观 注重学生参与,联系实际,丰富学生的感性认识,培养学生的良好的学习习惯
教学重点 能够根据实际问题,熟练地列出二次函数关系式,并求出函数的自变量的取值范围
教学难点 能够根据实际问题,熟练地列出二次函数关系式,并求出函数的自变量的取值范围
板书设计 知识回顾 四、课堂练习函数类型 五、课堂小结三、例题讲解 六、布置作业
教学过程设计
教 学 过 程 设计意图 个性思考栏
基础回顾 什么叫函数 在某变化过程中的两个变量x、y,当变量x在某个范围内取一个确定的值,另一个变量y总有唯一的值与它对应。 这样的两个变量之间的关系我们把它叫做函数关系。 对于上述变量x 、y,我们把y叫x的函数。 x叫自变量, y叫因变量。目前,我们已经学习了那几种类型的函数?函数的类型问题1:正方体六个面是全等的正方形,设正方体棱长为 x,表面积为 y,则 y 关于x 的关系式为 . 实际问题导入,体现新知识的产生源于生活实际的需要。
教 学 过 程 设计意图 个性思考栏
此式表示了正方体表面积y与正方体棱长x之间的关系,对于y的每一个值,x都有唯一的一个对应值,即y是x的函数。问题2:n个球队参加比赛,每两个队之间进行一场比赛,比赛的场次数m与球队数n有什么关系?每个球队n要与其他(n-1)个球队各比赛一场,甲队对乙队的比赛与乙队对甲队的比赛时同一场比赛,所以比赛的场次数 即:此式表示了比赛的场次数m与球队数n之间的关系,对于n的每一个值,m都有唯一的一个对应值,即m是n的函数。问题3:多边形的对角线数d与边数n有什么关系?式子①②③④有什么共同点 一般地,形如(a,b,c是常数,a≠ 0)的函数叫做二次函数。其中a为二次项系数,b为一次项系数,c为常数项。定义:一般地,形如(a,b,c是常数,a≠ 0)的函数叫做x的二次函数。注意:等号左边是变量y,右边是关于自变量x的整式。a,b,c为常数,且。等式的右边最高次数为2 ,可以没有一次项和常 数项,但不能没有二次项。x的取值范围是 任意实数。例题讲解例1、下列函数中,哪些是二次函数?若是,分别指出二次项系数,一次项系数,常数项. (2) (4) (6)四、课堂练习已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析式。五、课堂小结对自己说,你有什么收获 对老师说,你有什么疑惑 对同学说,你有什么温馨提示 知识应用 1、一农民用40m长的篱笆围成一个一边靠墙的长方形菜园,和墙垂直的一边长为Xm,菜园的面积为Ym2,求y与x之间的函数关系式,并说出自变量的取值范围。当x=12m时,计算菜园的面积。六、布置作业 结合实例更利于学生理解和接受新知识的产生与应用,经理探究能更好地运用所学知识解答实际问 题。巩固练习,运用新知。
课后反思:
科目 数学 拟授课班级
主备人 拟授课教师
拟授课时间
教学内容 22.1.1二次函数
教案课时 1课时 教学准备 多媒体
教学目标 知识与技能 能够根据实际问题,熟练地列出二次函数关系式,并求出函数的自变量的取值范围。
过程与方法 通过实际问题的探究,认识二次函数,认识二次项、一次项、常数项。
情感态度价值观 注重学生参与,联系实际,丰富学生的感性认识,培养学生的良好的学习习惯
教学重点 能够根据实际问题,熟练地列出二次函数关系式,并求出函数的自变量的取值范围
教学难点 能够根据实际问题,熟练地列出二次函数关系式,并求出函数的自变量的取值范围
板书设计 知识回顾 四、课堂练习函数类型 五、课堂小结三、例题讲解 六、布置作业
教学过程设计
教 学 过 程 设计意图 个性思考栏
基础回顾 什么叫函数 在某变化过程中的两个变量x、y,当变量x在某个范围内取一个确定的值,另一个变量y总有唯一的值与它对应。 这样的两个变量之间的关系我们把它叫做函数关系。 对于上述变量x 、y,我们把y叫x的函数。 x叫自变量, y叫因变量。目前,我们已经学习了那几种类型的函数?函数的类型问题1:正方体六个面是全等的正方形,设正方体棱长为 x,表面积为 y,则 y 关于x 的关系式为 . 实际问题导入,体现新知识的产生源于生活实际的需要。
教 学 过 程 设计意图 个性思考栏
此式表示了正方体表面积y与正方体棱长x之间的关系,对于y的每一个值,x都有唯一的一个对应值,即y是x的函数。问题2:n个球队参加比赛,每两个队之间进行一场比赛,比赛的场次数m与球队数n有什么关系?每个球队n要与其他(n-1)个球队各比赛一场,甲队对乙队的比赛与乙队对甲队的比赛时同一场比赛,所以比赛的场次数 即:此式表示了比赛的场次数m与球队数n之间的关系,对于n的每一个值,m都有唯一的一个对应值,即m是n的函数。问题3:多边形的对角线数d与边数n有什么关系?式子①②③④有什么共同点 一般地,形如(a,b,c是常数,a≠ 0)的函数叫做二次函数。其中a为二次项系数,b为一次项系数,c为常数项。定义:一般地,形如(a,b,c是常数,a≠ 0)的函数叫做x的二次函数。注意:等号左边是变量y,右边是关于自变量x的整式。a,b,c为常数,且。等式的右边最高次数为2 ,可以没有一次项和常 数项,但不能没有二次项。x的取值范围是 任意实数。例题讲解例1、下列函数中,哪些是二次函数?若是,分别指出二次项系数,一次项系数,常数项. (2) (4) (6)四、课堂练习已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析式。五、课堂小结对自己说,你有什么收获 对老师说,你有什么疑惑 对同学说,你有什么温馨提示 知识应用 1、一农民用40m长的篱笆围成一个一边靠墙的长方形菜园,和墙垂直的一边长为Xm,菜园的面积为Ym2,求y与x之间的函数关系式,并说出自变量的取值范围。当x=12m时,计算菜园的面积。六、布置作业 结合实例更利于学生理解和接受新知识的产生与应用,经理探究能更好地运用所学知识解答实际问 题。巩固练习,运用新知。
课后反思:
同课章节目录
