八年级上册第四章图形与坐标专题复习讲义
文档属性
| 名称 | 八年级上册第四章图形与坐标专题复习讲义 |  | |
| 格式 | zip | ||
| 文件大小 | 895.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-04 15:29:49 | ||
图片预览



文档简介
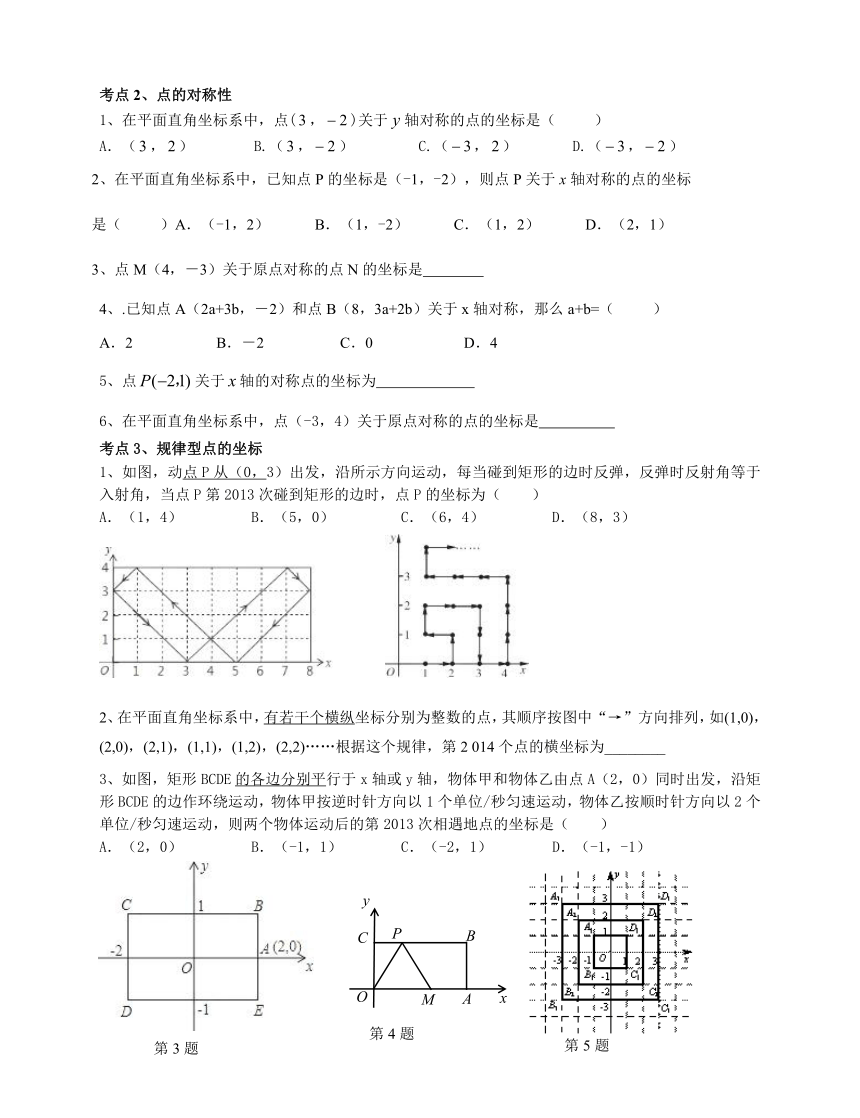
八年级第四章《图形与坐标》复习讲义
一、基础知识及考点剖析
1、、确定位置常用的方法:
一般由两种:1、 2、
2、平面直角坐标系:
(1)定义:具有 的两条 的数轴组成平面直角坐标系,两条数轴分别称 轴 轴或 轴 轴,这两系数轴把一个坐标平面分成的四个部分,我们称作是四个
(2)有序数对:在一个坐标平面内的任意一个点可以用一对 来表示,如A(a .b),(a .b)即为点A的 其中a是该点的 坐标,b是该点的 坐标平面内的点和有序数对具有 的关系。
(3)平面内点的坐标特征
① P(a .b):第一象限 第二象限 第三象限 第四象限 x轴上 y轴上
③特殊位置点的特点:P(a .b)若在一、三象限角的平分线上,则 若在二、四象限角的平分线上,则
④到坐标轴的距离:P(a .b)到x轴的距离 到y轴的距离 到原点的距离
⑤坐标平面内点的平移:将点P(a .b)向左(或右)平移h个单位,对应点坐标为
(或 ),向上(或下)平移k个单位,对应点坐标为
(或 )
⑥在平面上平移形图形时,我们通常是抓住_________________进行平移。
考点1、平面直角坐标系中点的特征.
1、如果m是任意实数,则点P(m-4,m+1)一定不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2、在平面直角坐标系中,点P(-2,x2+1)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3、点P(m+3,m+1)在直角坐标系的x轴上,则点P的坐标为( )
A.(0,2) B.(2,0) C.(4,0) D.(0,-2)
4、( )
5、已知点M(a,3-a)是第二象限的点,则a的取值范围是
6、点?P(a,a-3)在第四象限,则a的取值范围是
考点2、点的对称性
1、在平面直角坐标系中,点(,)关于轴对称的点的坐标是( )
A.(,) B.(,) C.(,) D.(,)
2、在平面直角坐标系中,已知点P的坐标是(-1,-2),则点P关于x轴对称的点的坐标
是( )A.(-1,2) B.(1,-2) C.(1,2) D.(2,1)
3、点M(4,-3)关于原点对称的点N的坐标是
4、.已知点A(2a+3b,-2)和点B(8,3a+2b)关于x轴对称,那么a+b=( )
A.2 B.-2 C.0 D.4
5、点关于轴的对称点的坐标为
6、在平面直角坐标系中,点(-3,4)关于原点对称的点的坐标是
考点3、规律型点的坐标
1、如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2013次碰到矩形的边时,点P的坐标为( )
A.(1,4) B.(5,0) C.(6,4) D.(8,3)
2、在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)……根据这个规律,第2 014个点的横坐标为________
3、如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2013次相遇地点的坐标是( )
A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
4、如图,在平面直角坐标系中,为坐标原点,四边形是长方形,∥,
点、的坐标分别为,,是的中点,点在边上运
动。当是腰长为5的等腰三角形时,则点的坐标为
5、在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3每个正方形四条边上的整点的个数.按此规律推算出正方形A10B10C10D10四条边上的整点共有 个
二、课堂重难点题型精讲
题型1、平面直角坐标系中规律性题型
1.(2015春?鄂州校级期中)如图,一个粒子在第一象限和x,y轴的正半轴上运动,在第一秒内,它从原点运动到(0,1),接着它按图所示在x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…)且每秒运动一个单位长度,那么2010秒时,这个粒子所处位置为( )
A.(14,44) B.(15,44) C.(44,14) D.(44,15)
【解答】解:设粒子运动到A1,A2,…An时所用的间分别为a1,a2,…,an,an﹣a1=2×n+…+2×3+2×2=2 (2+3+4+…+n),
an=n(n+1),44×45=1980,故运动了1980秒时它到点A44(44,44);
则运动了2010秒时,粒子所处的位置为(14,44).
故选A.
2.(2012?济南)如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是( )
A.(2,0) B.(﹣1,1) C.(﹣2,1) D.(﹣1,﹣1)
【解答】解:矩形的长宽分别为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×=4,物体乙行的路程为12×=8,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×=8,物体乙行的路程为12×2×=16,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×=12,物体乙行的路程为12×3×=24,在A点相遇;
…
此时甲、乙回到原出发点,则每相遇三次,两点回到出发点,
∵2012÷3=670…2,
故两个物体运动后的第2012次相遇地点的是:第二次相遇地点,即物体甲行的路程为12×2×=8,物体乙行的路程为12×2×=16,在DE边相遇;
此时相遇点的坐标为:(﹣1,﹣1),
故选:D.
3.(2008?恩施州)将杨辉三角中的每一个数都换成分数,得到一个如图所示的分数三角形,称莱布尼茨三角形.若用有序实数对(m,n)表示第m行,从左到右第n个数,如(4,3)表示分数.那么(9,2)表示的分数是 .
【解答】解:观察图表可知以下规律:是第几行就有几个分数;每行每个分数的分子都是1;每行第一个分数的分母为行号,如第n行为,第二个的分母为;每行首尾对称.
故(9,2)表示第9行,从左到右第2个数,即=.故答案填:.
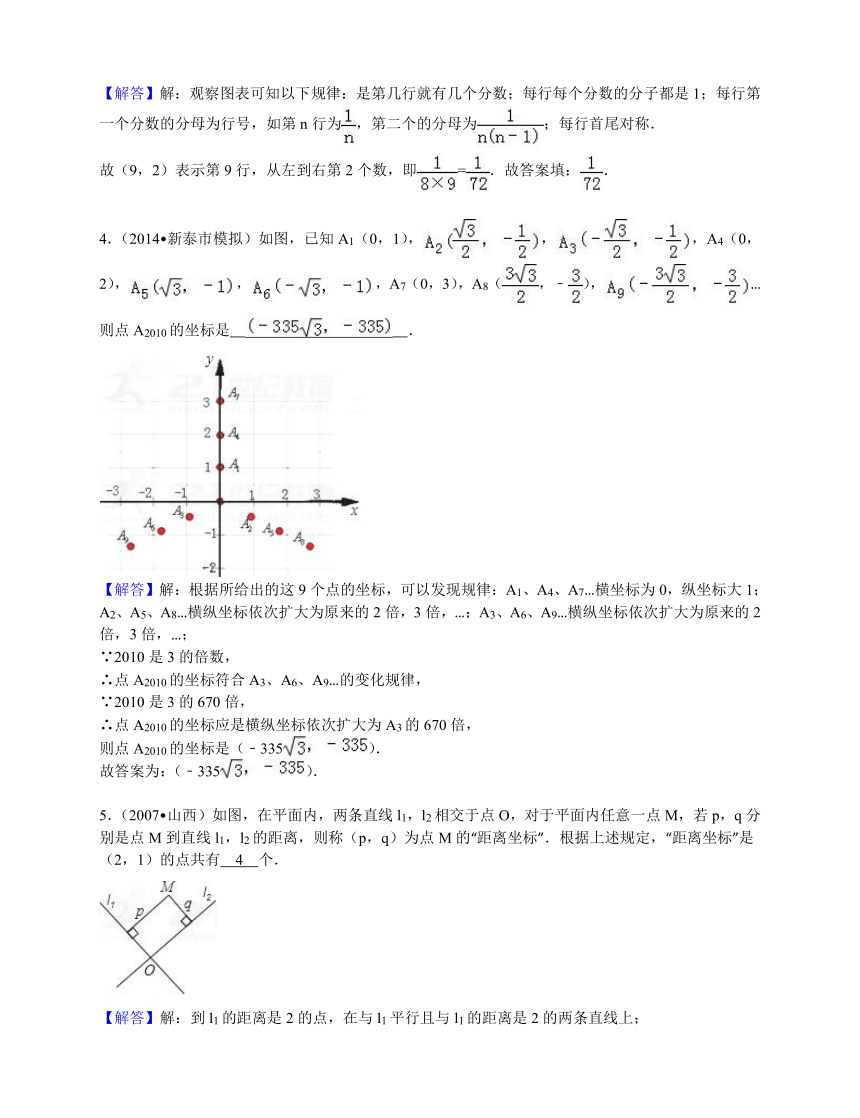
4.(2014?新泰市模拟)如图,已知A1(0,1),,,A4(0,2),,,A7(0,3),A8(,﹣),…则点A2010的坐标是 .
【解答】解:根据所给出的这9个点的坐标,可以发现规律:A1、A4、A7…横坐标为0,纵坐标大1;A2、A5、A8…横纵坐标依次扩大为原来的2倍,3倍,…;A3、A6、A9…横纵坐标依次扩大为原来的2倍,3倍,…;
∵2010是3的倍数,
∴点A2010的坐标符合A3、A6、A9…的变化规律,
∵2010是3的670倍,
∴点A2010的坐标应是横纵坐标依次扩大为A3的670倍,
则点A2010的坐标是(﹣335).
故答案为:(﹣335).
5.(2007?山西)如图,在平面内,两条直线l1,l2相交于点O,对于平面内任意一点M,若p,q分别是点M到直线l1,l2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(2,1)的点共有 4 个.
【解答】解:到l1的距离是2的点,在与l1平行且与l1的距离是2的两条直线上;
到l2的距离是1的点,在与l2平行且与l2的距离是1的两条直线上;
以上四条直线有四个交点,故“距离坐标”是(2,1)的点共有4个.
故答案为:4.
6.(2010?淅川县一模)如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第99次跳动至点P99的坐标是 (﹣25,50) ;点P第2009次跳动至点P2009的坐标是 (503,1005) .
【解答】解:由题中规律可得出如下结论:设点Pm的横坐标的绝对值是n,
则在y轴右侧的点的下标分别是4(n﹣1)和4n﹣3,
在y轴左侧的点的下标是:4n﹣2和4n﹣1;
判断P99的坐标,就是看99=4(n﹣1)和99=4n﹣3和99=4n﹣2和99=4n﹣1这四个式子中哪一个有负整数解,从而判断出点的横坐标.
由上可得:点P第99次跳动至点P99的坐标是(﹣25,50);点P第2009次跳动至点P2009的坐标是(503,1005).故两空分别填(﹣25,50)、(503,1005).
7.(2009?萧山区校级模拟)如图所示,在平面直角坐标系中,有若干个整数点,其顺序按图中箭头方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探索可得,第102个点的坐标为 (14,10) .
【解答】解:把第一个点(1,0)作为第一列,(2,1)和(2,0)作为第二列,依此类推,则第一列有一个数,第二列有2个数,第n列有n个数.则n列共有个数,并且在奇数列点的顺序是由上到下,偶数列点的顺序由下到上.
因为105=1+2+3+…+14,则第102个数一定在第14列,由下到上是第11个数.因而第102个点的坐标是(14,10).
故答案填:(14,10).
8.(2012?威海)如图,在平面直角坐标系中,线段OA1=1,OA1与x轴的夹角为30°,线段A1A2=1,A2A1⊥OA1,垂足为A1;线段A2A3=1,A3A2⊥A1A2,垂足为A2;线段A3A4=1,A4A3⊥A2A3,垂足为A3;…按此规律,点A2012的坐标为 (503﹣503,503+503) .
【解答】解:如图,过点A1作A1B⊥x轴,作A1C∥x轴A2C∥y轴,相交于点C,
∵OA1=1,OA1与x轴的夹角为30°,
∴OB=OA1?cos30°=1×=,
A1B=OA1?sin30°=1×=,
∴点A1的坐标为(,),
∵A2A1⊥OA1,OA1与x轴的夹角为30°,
∴∠OA1C=30°,∠A2A1C=90°﹣30°=60°,
∴∠A1A2C=90°﹣60°=30°,
同理可求:A2C=OB=,A1C=A1B=,
所以,点A2的坐标为(﹣,+),
点A3的坐标为(﹣+,++),即(﹣,+1),
点A4的坐标为(﹣﹣,+1+),即(﹣1,+1),
点A5的坐标为(﹣1+,+1+),即(﹣1,+),
点A6的坐标为(﹣1﹣,++),即(﹣,+),
…,
当n为奇数时,点An的坐标为(﹣,+),
当n为偶数时,点An的坐标为(﹣,+),
所以,当n=2012时,﹣=503﹣503,+=503+503,
点A2012的坐标为(503﹣503,503+503).
故答案为:(503﹣503,503+503).
9.(2013?聊城)如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (2n,1) (用n表示).
【解答】解:由图可知,n=1时,4×1+1=5,点A5(2,1),
n=2时,4×2+1=9,点A9(4,1),
n=3时,4×3+1=13,点A13(6,1),
所以,点A4n+1(2n,1).
故答案为:(2n,1).
10.(2015?黑龙江)如图,在平面直角坐标系中,点A(0,)、B(﹣1,0),过点A作AB的垂线交x轴于点A1,过点A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去,直至得到点A2015为止,则点A2015坐标为 (﹣31008,0), .
【解答】解:∵A(0,)、B(﹣1,0),
∴AB⊥AA1,
∴A1的坐标为:(3,0),
同理可得:A2的坐标为:(0,﹣3),A3的坐标为:(﹣9,0),
…
∵2015÷4=503…3,
∴点A2015坐标为(﹣31008,0),
故答案为:(﹣31008,0).
题型2、坐标平面的内的轴对称和平移变换相关题型
1.(2012?晋江市校级模拟)一个机器人从A0点出发朝正东方向走了2米到达A1点,记为第1次行走;接着,在A1处沿逆时针方向旋转60°后向前走2米到达A2点,记为第2次行走;再在A2处沿逆时针方向旋转60°后向前走2米到达A3点,记为第3次行走;依此类推,若点A0的坐标是(1,0),则该机器人第2012次行走后的坐标是( )
A.(0,) B.(3,0) C.(1,) D.(4,)
【解答】解:根据题意,每次都是逆时针旋转60°,
360°÷60°=6,
所以,旋转6次所走过的路线正好是正六边形,
∵2012÷6=335…2,
∴第2012次行走后与第2次行走到达的点相同,在点A2处,
过点作A2B⊥A0A1于点B,
∵每次前走2米,
∴A1B=A1A2?cos60°=2×=1,A2B=A1A2?sin60°=2×=,
∵点A0的坐标是(1,0),
∴点A2的横坐标为1+2+1=4,
点A2的坐标为(4,),
即第2012次行走后的坐标是(4,).
故选D.
2.(2012?河南模拟)如图,在平面直角坐标系中,点B的坐标为(0,3),∠AOB=90°,∠B=30°.将△AOB绕点O顺时针旋转一定角度后得到△A′OB′,并且点A′恰好好落到线段AB上,则点A′的坐标为 ( )
A.(﹣,) B.(﹣,) C.(﹣,) D.(﹣,)
【解答】解:∵点B的坐标为(0,3),
∴BO=3,
∵∠AOB=90°,∠B=30°,
∴AO=BO?tan30°=3×=,∠BAO=90°﹣30°=60°,
∵△A′OB′是由△ABC旋转得到,点A′在AB上,
∴A′O=AO,
∴△AOA′是等边三角形,
∴∠AOA′=60°,
过点A′作A′C⊥AO于点C,
则A′C=A′Osin60°=×=,OC=A′Ocos60°=×=,
∵点A′在第二象限,
∴点A′(﹣,).
故选D.
3.(2011春?灌阳县期末)平面直角坐标系中,将三角形各点的纵坐标都减去﹣3,横坐标保持不变,所得图形与原图形相比( )
A.向上平移了3个单位 B.向下平移了3个单位
C.向右平移了3个单位 D.向左平移了3个单位
【解答】解:各点的纵坐标都减去﹣3,也就是纵坐标加上3,
上下移动改变点的纵坐标,下减,上加,而点的横坐标保持不变,故所得图形与原图形相比向上平移了3个单位.
故选:A.
4.(2008?枣庄)如图,点A的坐标为(1,0),点B在直线y=﹣x上运动,当线段AB最短时,点B的坐标为( )
A.(0,0) B.(,﹣) C.(,﹣) D.(﹣,)
【解答】解:过A点作垂直于直线y=﹣x的垂线AB,
∵点B在直线y=﹣x上运动,
∴∠AOB=45°,
∴△AOB为等腰直角三角形,
过B作BC垂直x轴垂足为C,
则点C为OA的中点,
则OC=BC=.
作图可知B在x轴下方,y轴的右方.
∴横坐标为正,纵坐标为负.
所以当线段AB最短时,点B的坐标为(,﹣).
故选:B.
5.(2012?钦州)如图,直线y=﹣x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A旋转90°后得到△AO′B′,则点B′的坐标是 (﹣1,﹣2)或(5,2) .
【解答】解:当y=0时,﹣x+3=0,解得x=2,
当x=0时,y=3,
所以,点A(2,0),B(0,3),
所以,OA=2,OB=3,
根据旋转不变性可得△AOB≌△AO′B′,
∴AO′=OA=2,O′B′=OB=3,
①如果△AOB是逆时针旋转90°,则点B′(﹣1,﹣2),
②如果△AOB是顺时针旋转90°,则点B′(5,2),
综上,点B′的坐标是(﹣1,﹣2)或(5,2).
故答案为:(﹣1,﹣2)或(5,2).
6.(2009?嘉兴)如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形①,②,③,④…,则三角形⑩的直角顶点的坐标为 (36,0) .
【解答】解:由原图到图③,相当于向右平移了12个单位长度,象这样平移三次直角顶点是(36,0),再旋转一次到三角形⑩,直角顶点仍然是(36,0),则三角形⑩的直角顶点的坐标为(36,0).
故答案为:(36,0).
7.(2004?郑州)若点P(a+b,﹣5)与(1,3a﹣b)关于原点对称,则关于x的二次三项式x2﹣2ax﹣可以分解为 (x﹣1)2 .
【解答】解:根据“关于原点对称的点,横坐标与纵坐标都互为相反数”可知:
a+b=﹣1,3a﹣b=5,解得a=1,b=﹣2,
所以x2﹣2ax﹣=x2﹣2x+1=(x﹣1)2.
8.(2013?青海)如图,将△AOB绕点O逆时针旋转90°,得到△A′OB′.若点A的坐标为(a,b),则点A′的坐标为 (﹣b,a) .
【解答】解:由图易知A′B′=AB=b,OB′=OB=a,∠A′B′0=∠ABO=90°,
∵点A'在第二象限,
∴A'的坐标为(﹣b,a).
9.(2010?宁波模拟)已知如图,在平面直角坐标系中有四点,坐标分别为A(﹣4,3)、B(4,3)、M(0,1)、Q(1,2),动点P在线段AB上,从点A出发向点B以每秒1个单位运动.连接PM、PQ并延长分别交x轴于C、D两点(如图).
(1)在点P移动的过程中,若点M、C、D、Q能围成四边形,则t的取值范围是 0≤t≤8,且t≠6 ,并写出当t=2时,点C的坐标 (1、0) .
(2)在点P移动的过程中,△PMQ可能是轴对称图形吗?若能,请求出符合条件的点P的坐标;若不能,请说明理由.
(3)在点P移动的过程中,求四边形MCDQ的面积S的范围.
【解答】解:(1)0≤t≤8,且t≠6;点C的坐标为(1,0);
(2)若△PMQ可能是轴对称图形,则△PMQ必为等腰三角形.
①当PQ=QM时,设P点坐标为P(a,3),则有:
PQ==,
易知MQ=,
∴=,
解得a=2,a=0,
当a=2时,AP=4+2=6,即t=6不合题意,舍去.
∴P点坐标为(0,3);
②当PM=PQ时,设P点坐标为P(b,3),则有:
PQ=,PM=,
∴=,
解得b=﹣1,
∴P点坐标为(﹣1,3).
综上所述:点P的坐标为(﹣1、3)、(0、3);
(3)当0≤t<4时,S=﹣t+,Smax=.
当4≤t≤5时,S=﹣t+,Smax=;
当5<t≤8,S=t﹣,Smax=;
∴四边形MCDQ的面积S的范围是0<S≤.
10.(2008?铜仁地区)如图,在直角坐标系中,△ABC满足,∠C=90°,AC=4,BC=2,点A、C分别在x、y轴上,当A点从原点开始在x轴正半轴上运动时,点C随着在y轴正半轴上运动.
(1)当A点在原点时,求原点O到点B的距离OB;
(2)当OA=OC时,求原点O到点B的距离OB.
【解答】解:当A点在原点时,AC在y轴上,BC⊥y轴,所以
OB=AB==2;
(2)当OA=OC时,△OAC是等腰直角三角形
AC=4,OA=OC=2.
过点B作BE⊥OA于E,过点C作CD⊥OC,且CD与BE交于点D,
∵∠2+∠ACD=90°,∠3+∠ACD=90°,
∴∠2=∠3,
∵∠1=∠2=45°,
∴∠3=45°,
∴△CDB是等腰直角三角形,
∵CD=BD,
BC=2,CD=BD=.
BE=BD+DE=BD+OC=3,OB==2.
三、课堂举一反三精炼
选择题
1.在平面直角坐标系中,点(1,2)所在的象限是( )
A.第一象限; B.第二象限; C.第三象限; D.第四象限.
2.在平面直角坐标系xOy中,点P(-3,5)关于y轴的对称点在第( )象限
A、一 B、二 C、三 D、四
3.将△ABC的三个顶点的横坐标不变,纵坐标乘以-1,则所得图形 ( )
A、与原图形关于x轴对称 B、与原图形关于y轴对称
C、与原图形关于原点对称 D、向轴的负方向平移了一个单位
坐标平面上有一点A,且A点到x轴的距离为3,A点到y轴的距离恰为到x轴距离的
3倍.若A点在第二象限,则A点坐标为何?( )
A.(-9,3) B.(-3,1) C.(-3,9) D.(-1,3)
5.点关于轴对称的点的坐标为( )
A. B. C. D.
6.在如图所示的直角坐标系中,M、N的坐标分别为( )
A. M(-1,2),N(2, 1) B.M(2,-1),N(2,1)
C.M(-1,2),N(1, 2) D.M(2,-1),N(1,2)
将三角形三个顶点的横坐标都减2,纵坐标不变,则所得三角
形与原三角形的关系是( )
A.将原图向左平移两个单位 B.关于原点对称
C.将原图向右平移两个单位 D.关于轴对称
8. 点在第二象限内,到轴的距离是4,到轴的距离是3,那么点的坐标为( )
A. B. C. D.
9. 平行四边形OABC在平面直角坐标系中的位置如图所示,
,,则点B的坐标是( )
A.(3,1) B.(1,3) C. (2,1) D.(1,2)
10..如图,矩形OABC的边OA、OC分别在轴、轴上,点B的坐标为.点D、E分别在AB、BC边上,BD=BE=1.沿直线DE将△BDE翻折,点B落在B′处.则点B′的坐标为( )
A. B. C. D.
二.填空题
11.点关于轴的对称点的坐标是
12.如果a、b同号,则点P(a,b)在 象限.
13.已知点A(m2+1,n2-2)与点B(2m,4n+6)关于原点对称,则A关于x 轴的对称点的坐标为_____,B关于y轴的对称点的坐标为______
14.已知O(0, 0),A(-3, 0),B(-1, -2),则△AOB的面积为______
15.若点A在第二象限,且A点到x轴的距离为3,到y轴的距离为4,则点A的坐标为 ____
16.如图,在直角坐标系中,已知点A(-4,0),B(0,3),对△OAB连续作旋转变换,依
次得到三角形(1)、三角形(2)、三角形(3)、三角形(4)、…,
(1)△AOB的面积是
(2)三角形(2013)的直角顶点的坐标是____________
解答题
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段和直线,点均在小正方形的顶点上.
(1)在方格纸中画四边形(四边形的各顶点均在小正方形的顶点上),使四边形是以直线为对称轴的轴对称图形,点的对称点为点,点的对称点为点;(2)请直接写出四边形的周长和面积.
18.如图,在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:(1)将△ABC向右平移5个单位长度,画出平移后的△A1B1C1;
(2)画出△ABC关于x轴对称的△A2B2C2.
19.如图:在平面直角坐标系中,△ABC的三个顶点的坐标分别为
A(-3,2),B(-4,-3),C(-1,-1).
画出△ABC关于y轴对称的△A1B1C1;
写出△A1B1C1各顶点的坐标。
20.在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为(,).运用:(1)如图,矩形ONEF的对角线交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为______;
(2)在直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.
21..如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5,矩形以每秒2个单位长度沿x轴正方向做匀速运动.同时点P从A点出发以每秒1个单位长度沿A─B─C─D的路线做匀速运动.当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
(1)求P点从A点运动到D点所需的时间;
(2)设P点运动时间为t(s);
①当t=5时,求出点P的坐标;
②若△ODP的面积为S,试求出S与t之间的函数关系式(并写出相应的自量
t的取值范围).
22.在平面直角坐标系中,点M的坐标为(a,1-2a).
(1)当a=-1时,点M在坐标系的第________象限(直接填写答案);
(2)将点M向左平移2个单位长度,再向上平移1个单位长度后得到点N.当点N在第三象限时,求a的取值范围.
23.某乡镇为了解决抗旱问题,要在某河道建一座水泵站,分别向河同一侧的张村A和李村B送水.经实地勘查后,工程人员设计图纸时,以河道上的大桥O为坐标原点,以河道所在的直线为x轴,建立平面直角坐标系(如图6-1-20),两村的坐标分别为A(2,3),B(12,7).
(1)若从节约经费考虑,水泵站建在距离大桥O多远的地方,可使所用输水管最短?
(2)水泵站建在距离大桥O多远的地方,可使它到张村、李村的距离相等?
选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
A
A
A
D
A
D
A
C
A
B
解答题
17.(1)如图
(2) 周长为
面积为
18.解:如图:
19.(1)如图:
21.解(1)
(2)①
②
22.解:(1)由a=-1,得1-2a=3,
∴M在第二象限.
(2)平移后点N的坐标为(a-2,2-2a),
又点N在第三象限,∴解得1<a<2.
23.解:(1)如图,作点B关于x轴的对称点E,连接AE,则点E为(12,-7).
设直线AE的函数关系式为y=kx+b,则
解得
∴直线AE的解析式为y=-x+5.
当y=0时,x=5.
所以,当水泵站应建在距离大桥5千米的地方时,可使所用输水管道最短.
(2)如图作线段AB的垂直平分线GF,交AB 于点F,交x轴于点G,设点G的坐标为(x,0).
在Rt△AGD中,AG2=AD2+DG2=9+(x-2)2.
一、基础知识及考点剖析
1、、确定位置常用的方法:
一般由两种:1、 2、
2、平面直角坐标系:
(1)定义:具有 的两条 的数轴组成平面直角坐标系,两条数轴分别称 轴 轴或 轴 轴,这两系数轴把一个坐标平面分成的四个部分,我们称作是四个
(2)有序数对:在一个坐标平面内的任意一个点可以用一对 来表示,如A(a .b),(a .b)即为点A的 其中a是该点的 坐标,b是该点的 坐标平面内的点和有序数对具有 的关系。
(3)平面内点的坐标特征
① P(a .b):第一象限 第二象限 第三象限 第四象限 x轴上 y轴上
③特殊位置点的特点:P(a .b)若在一、三象限角的平分线上,则 若在二、四象限角的平分线上,则
④到坐标轴的距离:P(a .b)到x轴的距离 到y轴的距离 到原点的距离
⑤坐标平面内点的平移:将点P(a .b)向左(或右)平移h个单位,对应点坐标为
(或 ),向上(或下)平移k个单位,对应点坐标为
(或 )
⑥在平面上平移形图形时,我们通常是抓住_________________进行平移。
考点1、平面直角坐标系中点的特征.
1、如果m是任意实数,则点P(m-4,m+1)一定不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2、在平面直角坐标系中,点P(-2,x2+1)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3、点P(m+3,m+1)在直角坐标系的x轴上,则点P的坐标为( )
A.(0,2) B.(2,0) C.(4,0) D.(0,-2)
4、( )
5、已知点M(a,3-a)是第二象限的点,则a的取值范围是
6、点?P(a,a-3)在第四象限,则a的取值范围是
考点2、点的对称性
1、在平面直角坐标系中,点(,)关于轴对称的点的坐标是( )
A.(,) B.(,) C.(,) D.(,)
2、在平面直角坐标系中,已知点P的坐标是(-1,-2),则点P关于x轴对称的点的坐标
是( )A.(-1,2) B.(1,-2) C.(1,2) D.(2,1)
3、点M(4,-3)关于原点对称的点N的坐标是
4、.已知点A(2a+3b,-2)和点B(8,3a+2b)关于x轴对称,那么a+b=( )
A.2 B.-2 C.0 D.4
5、点关于轴的对称点的坐标为
6、在平面直角坐标系中,点(-3,4)关于原点对称的点的坐标是
考点3、规律型点的坐标
1、如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2013次碰到矩形的边时,点P的坐标为( )
A.(1,4) B.(5,0) C.(6,4) D.(8,3)
2、在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)……根据这个规律,第2 014个点的横坐标为________
3、如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2013次相遇地点的坐标是( )
A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
4、如图,在平面直角坐标系中,为坐标原点,四边形是长方形,∥,
点、的坐标分别为,,是的中点,点在边上运
动。当是腰长为5的等腰三角形时,则点的坐标为
5、在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3每个正方形四条边上的整点的个数.按此规律推算出正方形A10B10C10D10四条边上的整点共有 个
二、课堂重难点题型精讲
题型1、平面直角坐标系中规律性题型
1.(2015春?鄂州校级期中)如图,一个粒子在第一象限和x,y轴的正半轴上运动,在第一秒内,它从原点运动到(0,1),接着它按图所示在x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…)且每秒运动一个单位长度,那么2010秒时,这个粒子所处位置为( )
A.(14,44) B.(15,44) C.(44,14) D.(44,15)
【解答】解:设粒子运动到A1,A2,…An时所用的间分别为a1,a2,…,an,an﹣a1=2×n+…+2×3+2×2=2 (2+3+4+…+n),
an=n(n+1),44×45=1980,故运动了1980秒时它到点A44(44,44);
则运动了2010秒时,粒子所处的位置为(14,44).
故选A.
2.(2012?济南)如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是( )
A.(2,0) B.(﹣1,1) C.(﹣2,1) D.(﹣1,﹣1)
【解答】解:矩形的长宽分别为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×=4,物体乙行的路程为12×=8,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×=8,物体乙行的路程为12×2×=16,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×=12,物体乙行的路程为12×3×=24,在A点相遇;
…
此时甲、乙回到原出发点,则每相遇三次,两点回到出发点,
∵2012÷3=670…2,
故两个物体运动后的第2012次相遇地点的是:第二次相遇地点,即物体甲行的路程为12×2×=8,物体乙行的路程为12×2×=16,在DE边相遇;
此时相遇点的坐标为:(﹣1,﹣1),
故选:D.
3.(2008?恩施州)将杨辉三角中的每一个数都换成分数,得到一个如图所示的分数三角形,称莱布尼茨三角形.若用有序实数对(m,n)表示第m行,从左到右第n个数,如(4,3)表示分数.那么(9,2)表示的分数是 .
【解答】解:观察图表可知以下规律:是第几行就有几个分数;每行每个分数的分子都是1;每行第一个分数的分母为行号,如第n行为,第二个的分母为;每行首尾对称.
故(9,2)表示第9行,从左到右第2个数,即=.故答案填:.
4.(2014?新泰市模拟)如图,已知A1(0,1),,,A4(0,2),,,A7(0,3),A8(,﹣),…则点A2010的坐标是 .
【解答】解:根据所给出的这9个点的坐标,可以发现规律:A1、A4、A7…横坐标为0,纵坐标大1;A2、A5、A8…横纵坐标依次扩大为原来的2倍,3倍,…;A3、A6、A9…横纵坐标依次扩大为原来的2倍,3倍,…;
∵2010是3的倍数,
∴点A2010的坐标符合A3、A6、A9…的变化规律,
∵2010是3的670倍,
∴点A2010的坐标应是横纵坐标依次扩大为A3的670倍,
则点A2010的坐标是(﹣335).
故答案为:(﹣335).
5.(2007?山西)如图,在平面内,两条直线l1,l2相交于点O,对于平面内任意一点M,若p,q分别是点M到直线l1,l2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(2,1)的点共有 4 个.
【解答】解:到l1的距离是2的点,在与l1平行且与l1的距离是2的两条直线上;
到l2的距离是1的点,在与l2平行且与l2的距离是1的两条直线上;
以上四条直线有四个交点,故“距离坐标”是(2,1)的点共有4个.
故答案为:4.
6.(2010?淅川县一模)如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第99次跳动至点P99的坐标是 (﹣25,50) ;点P第2009次跳动至点P2009的坐标是 (503,1005) .
【解答】解:由题中规律可得出如下结论:设点Pm的横坐标的绝对值是n,
则在y轴右侧的点的下标分别是4(n﹣1)和4n﹣3,
在y轴左侧的点的下标是:4n﹣2和4n﹣1;
判断P99的坐标,就是看99=4(n﹣1)和99=4n﹣3和99=4n﹣2和99=4n﹣1这四个式子中哪一个有负整数解,从而判断出点的横坐标.
由上可得:点P第99次跳动至点P99的坐标是(﹣25,50);点P第2009次跳动至点P2009的坐标是(503,1005).故两空分别填(﹣25,50)、(503,1005).
7.(2009?萧山区校级模拟)如图所示,在平面直角坐标系中,有若干个整数点,其顺序按图中箭头方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探索可得,第102个点的坐标为 (14,10) .
【解答】解:把第一个点(1,0)作为第一列,(2,1)和(2,0)作为第二列,依此类推,则第一列有一个数,第二列有2个数,第n列有n个数.则n列共有个数,并且在奇数列点的顺序是由上到下,偶数列点的顺序由下到上.
因为105=1+2+3+…+14,则第102个数一定在第14列,由下到上是第11个数.因而第102个点的坐标是(14,10).
故答案填:(14,10).
8.(2012?威海)如图,在平面直角坐标系中,线段OA1=1,OA1与x轴的夹角为30°,线段A1A2=1,A2A1⊥OA1,垂足为A1;线段A2A3=1,A3A2⊥A1A2,垂足为A2;线段A3A4=1,A4A3⊥A2A3,垂足为A3;…按此规律,点A2012的坐标为 (503﹣503,503+503) .
【解答】解:如图,过点A1作A1B⊥x轴,作A1C∥x轴A2C∥y轴,相交于点C,
∵OA1=1,OA1与x轴的夹角为30°,
∴OB=OA1?cos30°=1×=,
A1B=OA1?sin30°=1×=,
∴点A1的坐标为(,),
∵A2A1⊥OA1,OA1与x轴的夹角为30°,
∴∠OA1C=30°,∠A2A1C=90°﹣30°=60°,
∴∠A1A2C=90°﹣60°=30°,
同理可求:A2C=OB=,A1C=A1B=,
所以,点A2的坐标为(﹣,+),
点A3的坐标为(﹣+,++),即(﹣,+1),
点A4的坐标为(﹣﹣,+1+),即(﹣1,+1),
点A5的坐标为(﹣1+,+1+),即(﹣1,+),
点A6的坐标为(﹣1﹣,++),即(﹣,+),
…,
当n为奇数时,点An的坐标为(﹣,+),
当n为偶数时,点An的坐标为(﹣,+),
所以,当n=2012时,﹣=503﹣503,+=503+503,
点A2012的坐标为(503﹣503,503+503).
故答案为:(503﹣503,503+503).
9.(2013?聊城)如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (2n,1) (用n表示).
【解答】解:由图可知,n=1时,4×1+1=5,点A5(2,1),
n=2时,4×2+1=9,点A9(4,1),
n=3时,4×3+1=13,点A13(6,1),
所以,点A4n+1(2n,1).
故答案为:(2n,1).
10.(2015?黑龙江)如图,在平面直角坐标系中,点A(0,)、B(﹣1,0),过点A作AB的垂线交x轴于点A1,过点A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去,直至得到点A2015为止,则点A2015坐标为 (﹣31008,0), .
【解答】解:∵A(0,)、B(﹣1,0),
∴AB⊥AA1,
∴A1的坐标为:(3,0),
同理可得:A2的坐标为:(0,﹣3),A3的坐标为:(﹣9,0),
…
∵2015÷4=503…3,
∴点A2015坐标为(﹣31008,0),
故答案为:(﹣31008,0).
题型2、坐标平面的内的轴对称和平移变换相关题型
1.(2012?晋江市校级模拟)一个机器人从A0点出发朝正东方向走了2米到达A1点,记为第1次行走;接着,在A1处沿逆时针方向旋转60°后向前走2米到达A2点,记为第2次行走;再在A2处沿逆时针方向旋转60°后向前走2米到达A3点,记为第3次行走;依此类推,若点A0的坐标是(1,0),则该机器人第2012次行走后的坐标是( )
A.(0,) B.(3,0) C.(1,) D.(4,)
【解答】解:根据题意,每次都是逆时针旋转60°,
360°÷60°=6,
所以,旋转6次所走过的路线正好是正六边形,
∵2012÷6=335…2,
∴第2012次行走后与第2次行走到达的点相同,在点A2处,
过点作A2B⊥A0A1于点B,
∵每次前走2米,
∴A1B=A1A2?cos60°=2×=1,A2B=A1A2?sin60°=2×=,
∵点A0的坐标是(1,0),
∴点A2的横坐标为1+2+1=4,
点A2的坐标为(4,),
即第2012次行走后的坐标是(4,).
故选D.
2.(2012?河南模拟)如图,在平面直角坐标系中,点B的坐标为(0,3),∠AOB=90°,∠B=30°.将△AOB绕点O顺时针旋转一定角度后得到△A′OB′,并且点A′恰好好落到线段AB上,则点A′的坐标为 ( )
A.(﹣,) B.(﹣,) C.(﹣,) D.(﹣,)
【解答】解:∵点B的坐标为(0,3),
∴BO=3,
∵∠AOB=90°,∠B=30°,
∴AO=BO?tan30°=3×=,∠BAO=90°﹣30°=60°,
∵△A′OB′是由△ABC旋转得到,点A′在AB上,
∴A′O=AO,
∴△AOA′是等边三角形,
∴∠AOA′=60°,
过点A′作A′C⊥AO于点C,
则A′C=A′Osin60°=×=,OC=A′Ocos60°=×=,
∵点A′在第二象限,
∴点A′(﹣,).
故选D.
3.(2011春?灌阳县期末)平面直角坐标系中,将三角形各点的纵坐标都减去﹣3,横坐标保持不变,所得图形与原图形相比( )
A.向上平移了3个单位 B.向下平移了3个单位
C.向右平移了3个单位 D.向左平移了3个单位
【解答】解:各点的纵坐标都减去﹣3,也就是纵坐标加上3,
上下移动改变点的纵坐标,下减,上加,而点的横坐标保持不变,故所得图形与原图形相比向上平移了3个单位.
故选:A.
4.(2008?枣庄)如图,点A的坐标为(1,0),点B在直线y=﹣x上运动,当线段AB最短时,点B的坐标为( )
A.(0,0) B.(,﹣) C.(,﹣) D.(﹣,)
【解答】解:过A点作垂直于直线y=﹣x的垂线AB,
∵点B在直线y=﹣x上运动,
∴∠AOB=45°,
∴△AOB为等腰直角三角形,
过B作BC垂直x轴垂足为C,
则点C为OA的中点,
则OC=BC=.
作图可知B在x轴下方,y轴的右方.
∴横坐标为正,纵坐标为负.
所以当线段AB最短时,点B的坐标为(,﹣).
故选:B.
5.(2012?钦州)如图,直线y=﹣x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A旋转90°后得到△AO′B′,则点B′的坐标是 (﹣1,﹣2)或(5,2) .
【解答】解:当y=0时,﹣x+3=0,解得x=2,
当x=0时,y=3,
所以,点A(2,0),B(0,3),
所以,OA=2,OB=3,
根据旋转不变性可得△AOB≌△AO′B′,
∴AO′=OA=2,O′B′=OB=3,
①如果△AOB是逆时针旋转90°,则点B′(﹣1,﹣2),
②如果△AOB是顺时针旋转90°,则点B′(5,2),
综上,点B′的坐标是(﹣1,﹣2)或(5,2).
故答案为:(﹣1,﹣2)或(5,2).
6.(2009?嘉兴)如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形①,②,③,④…,则三角形⑩的直角顶点的坐标为 (36,0) .
【解答】解:由原图到图③,相当于向右平移了12个单位长度,象这样平移三次直角顶点是(36,0),再旋转一次到三角形⑩,直角顶点仍然是(36,0),则三角形⑩的直角顶点的坐标为(36,0).
故答案为:(36,0).
7.(2004?郑州)若点P(a+b,﹣5)与(1,3a﹣b)关于原点对称,则关于x的二次三项式x2﹣2ax﹣可以分解为 (x﹣1)2 .
【解答】解:根据“关于原点对称的点,横坐标与纵坐标都互为相反数”可知:
a+b=﹣1,3a﹣b=5,解得a=1,b=﹣2,
所以x2﹣2ax﹣=x2﹣2x+1=(x﹣1)2.
8.(2013?青海)如图,将△AOB绕点O逆时针旋转90°,得到△A′OB′.若点A的坐标为(a,b),则点A′的坐标为 (﹣b,a) .
【解答】解:由图易知A′B′=AB=b,OB′=OB=a,∠A′B′0=∠ABO=90°,
∵点A'在第二象限,
∴A'的坐标为(﹣b,a).
9.(2010?宁波模拟)已知如图,在平面直角坐标系中有四点,坐标分别为A(﹣4,3)、B(4,3)、M(0,1)、Q(1,2),动点P在线段AB上,从点A出发向点B以每秒1个单位运动.连接PM、PQ并延长分别交x轴于C、D两点(如图).
(1)在点P移动的过程中,若点M、C、D、Q能围成四边形,则t的取值范围是 0≤t≤8,且t≠6 ,并写出当t=2时,点C的坐标 (1、0) .
(2)在点P移动的过程中,△PMQ可能是轴对称图形吗?若能,请求出符合条件的点P的坐标;若不能,请说明理由.
(3)在点P移动的过程中,求四边形MCDQ的面积S的范围.
【解答】解:(1)0≤t≤8,且t≠6;点C的坐标为(1,0);
(2)若△PMQ可能是轴对称图形,则△PMQ必为等腰三角形.
①当PQ=QM时,设P点坐标为P(a,3),则有:
PQ==,
易知MQ=,
∴=,
解得a=2,a=0,
当a=2时,AP=4+2=6,即t=6不合题意,舍去.
∴P点坐标为(0,3);
②当PM=PQ时,设P点坐标为P(b,3),则有:
PQ=,PM=,
∴=,
解得b=﹣1,
∴P点坐标为(﹣1,3).
综上所述:点P的坐标为(﹣1、3)、(0、3);
(3)当0≤t<4时,S=﹣t+,Smax=.
当4≤t≤5时,S=﹣t+,Smax=;
当5<t≤8,S=t﹣,Smax=;
∴四边形MCDQ的面积S的范围是0<S≤.
10.(2008?铜仁地区)如图,在直角坐标系中,△ABC满足,∠C=90°,AC=4,BC=2,点A、C分别在x、y轴上,当A点从原点开始在x轴正半轴上运动时,点C随着在y轴正半轴上运动.
(1)当A点在原点时,求原点O到点B的距离OB;
(2)当OA=OC时,求原点O到点B的距离OB.
【解答】解:当A点在原点时,AC在y轴上,BC⊥y轴,所以
OB=AB==2;
(2)当OA=OC时,△OAC是等腰直角三角形
AC=4,OA=OC=2.
过点B作BE⊥OA于E,过点C作CD⊥OC,且CD与BE交于点D,
∵∠2+∠ACD=90°,∠3+∠ACD=90°,
∴∠2=∠3,
∵∠1=∠2=45°,
∴∠3=45°,
∴△CDB是等腰直角三角形,
∵CD=BD,
BC=2,CD=BD=.
BE=BD+DE=BD+OC=3,OB==2.
三、课堂举一反三精炼
选择题
1.在平面直角坐标系中,点(1,2)所在的象限是( )
A.第一象限; B.第二象限; C.第三象限; D.第四象限.
2.在平面直角坐标系xOy中,点P(-3,5)关于y轴的对称点在第( )象限
A、一 B、二 C、三 D、四
3.将△ABC的三个顶点的横坐标不变,纵坐标乘以-1,则所得图形 ( )
A、与原图形关于x轴对称 B、与原图形关于y轴对称
C、与原图形关于原点对称 D、向轴的负方向平移了一个单位
坐标平面上有一点A,且A点到x轴的距离为3,A点到y轴的距离恰为到x轴距离的
3倍.若A点在第二象限,则A点坐标为何?( )
A.(-9,3) B.(-3,1) C.(-3,9) D.(-1,3)
5.点关于轴对称的点的坐标为( )
A. B. C. D.
6.在如图所示的直角坐标系中,M、N的坐标分别为( )
A. M(-1,2),N(2, 1) B.M(2,-1),N(2,1)
C.M(-1,2),N(1, 2) D.M(2,-1),N(1,2)
将三角形三个顶点的横坐标都减2,纵坐标不变,则所得三角
形与原三角形的关系是( )
A.将原图向左平移两个单位 B.关于原点对称
C.将原图向右平移两个单位 D.关于轴对称
8. 点在第二象限内,到轴的距离是4,到轴的距离是3,那么点的坐标为( )
A. B. C. D.
9. 平行四边形OABC在平面直角坐标系中的位置如图所示,
,,则点B的坐标是( )
A.(3,1) B.(1,3) C. (2,1) D.(1,2)
10..如图,矩形OABC的边OA、OC分别在轴、轴上,点B的坐标为.点D、E分别在AB、BC边上,BD=BE=1.沿直线DE将△BDE翻折,点B落在B′处.则点B′的坐标为( )
A. B. C. D.
二.填空题
11.点关于轴的对称点的坐标是
12.如果a、b同号,则点P(a,b)在 象限.
13.已知点A(m2+1,n2-2)与点B(2m,4n+6)关于原点对称,则A关于x 轴的对称点的坐标为_____,B关于y轴的对称点的坐标为______
14.已知O(0, 0),A(-3, 0),B(-1, -2),则△AOB的面积为______
15.若点A在第二象限,且A点到x轴的距离为3,到y轴的距离为4,则点A的坐标为 ____
16.如图,在直角坐标系中,已知点A(-4,0),B(0,3),对△OAB连续作旋转变换,依
次得到三角形(1)、三角形(2)、三角形(3)、三角形(4)、…,
(1)△AOB的面积是
(2)三角形(2013)的直角顶点的坐标是____________
解答题
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段和直线,点均在小正方形的顶点上.
(1)在方格纸中画四边形(四边形的各顶点均在小正方形的顶点上),使四边形是以直线为对称轴的轴对称图形,点的对称点为点,点的对称点为点;(2)请直接写出四边形的周长和面积.
18.如图,在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:(1)将△ABC向右平移5个单位长度,画出平移后的△A1B1C1;
(2)画出△ABC关于x轴对称的△A2B2C2.
19.如图:在平面直角坐标系中,△ABC的三个顶点的坐标分别为
A(-3,2),B(-4,-3),C(-1,-1).
画出△ABC关于y轴对称的△A1B1C1;
写出△A1B1C1各顶点的坐标。
20.在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为(,).运用:(1)如图,矩形ONEF的对角线交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为______;
(2)在直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.
21..如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5,矩形以每秒2个单位长度沿x轴正方向做匀速运动.同时点P从A点出发以每秒1个单位长度沿A─B─C─D的路线做匀速运动.当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
(1)求P点从A点运动到D点所需的时间;
(2)设P点运动时间为t(s);
①当t=5时,求出点P的坐标;
②若△ODP的面积为S,试求出S与t之间的函数关系式(并写出相应的自量
t的取值范围).
22.在平面直角坐标系中,点M的坐标为(a,1-2a).
(1)当a=-1时,点M在坐标系的第________象限(直接填写答案);
(2)将点M向左平移2个单位长度,再向上平移1个单位长度后得到点N.当点N在第三象限时,求a的取值范围.
23.某乡镇为了解决抗旱问题,要在某河道建一座水泵站,分别向河同一侧的张村A和李村B送水.经实地勘查后,工程人员设计图纸时,以河道上的大桥O为坐标原点,以河道所在的直线为x轴,建立平面直角坐标系(如图6-1-20),两村的坐标分别为A(2,3),B(12,7).
(1)若从节约经费考虑,水泵站建在距离大桥O多远的地方,可使所用输水管最短?
(2)水泵站建在距离大桥O多远的地方,可使它到张村、李村的距离相等?
选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
A
A
A
D
A
D
A
C
A
B
解答题
17.(1)如图
(2) 周长为
面积为
18.解:如图:
19.(1)如图:
21.解(1)
(2)①
②
22.解:(1)由a=-1,得1-2a=3,
∴M在第二象限.
(2)平移后点N的坐标为(a-2,2-2a),
又点N在第三象限,∴解得1<a<2.
23.解:(1)如图,作点B关于x轴的对称点E,连接AE,则点E为(12,-7).
设直线AE的函数关系式为y=kx+b,则
解得
∴直线AE的解析式为y=-x+5.
当y=0时,x=5.
所以,当水泵站应建在距离大桥5千米的地方时,可使所用输水管道最短.
(2)如图作线段AB的垂直平分线GF,交AB 于点F,交x轴于点G,设点G的坐标为(x,0).
在Rt△AGD中,AG2=AD2+DG2=9+(x-2)2.
同课章节目录
