八年级上第五章一次函数专题复习讲义
图片预览




文档简介
八年级第五章《一次函数》专题复习讲义
一、基础知识及考点剖析
考点1、常量和变量
1.(2016春?迁安市期中)如果用总长为120m的篱笆围成一个长方形场地,设长方形的面积为S(m2),周长为C(m),一边长为a(m),那么S,C,a中是变量的是( )21世纪教育网版权所有
A.S和C B.S和a C.C和a D.S,C,a
【解答】解:S(m2),周长为C(m),一边长为a(m),那么S,a是变量,
故选:B.
2.(2015秋?上城区期末)在圆周长计算公式C=2πr中,对半径不同的圆,变量有( )
A.C,r B.C,π,r C.C,πr D.C,2π,r
【解答】解:在圆周长计算公式C=2πr中,对半径不同的圆,变量有:C,r.
故选:A.
3.(2014春?上街区校级期中)某公司销售部门发现,该公司的销售收入随销售量的变化而变化,其中 销售量 是自变量, 销售收入 是因变量.21教育网
【解答】解:根据题意知,公司的销售收入随销售量的变化而变化,
所以销售量是自变量,收入数为因变量.
故答案为:销售量,销售收入.
4.下表是小华做观察水的沸腾实验时所记录的数据:
(1)时间是8分钟时,水的温度为 100℃ ;
(2)此表反映了变量 温度 和 时间 之间的关系,其中 时间 是自变量, 温度 是因变量;
(3)在 0至8分钟 时间内,温度随时间增加而增加; 8至12分钟 时间内,水的温度不再变化.
【解答】解:(1)第8分钟时水的温度为100℃;
(2)反映的温度随着时间的变化而变化的,时间是自变量,温度是因变量;
(3)观察表格发现在0至8分钟时间内,温度随时间增加而增加;8至12分钟时间内,水的温度不再变化.
故答案为:(1)100℃(2)温度,时间,时间,温度;(3)0至8分钟,8至12分钟.
5.(2014春?通川区校级期中)已知某易拉罐厂设计一种易拉罐,在设计过程中发现符合要求的易拉罐的底面半径与铝用量有如下关系:21cnjy.com
底面半径x(cm)
1.6
2.0
2.4
2.8
3.2
3.6
4.0
用铝量y(cm3)
6.9
6.0
5.6
5.5
5.7
6.0
6.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当易拉罐底面半径为2.4cm时,易拉罐需要的用铝量是多少?
(3)根据表格中的数据,你认为易拉罐的底面半径为多少时比较适宜?说说你的理由.
(4)粗略说一说易拉罐底面半径对所需铝质量的影响.
【解答】解:(1)易拉罐底面半径和用铝量的关系,易拉罐底面半径为自变量,用铝量为因变量;
(2)当底面半径为2.4cm时,易拉罐的用铝量为5.6cm3
(3)易拉罐底面半径为2.8cm时比较合适,因为此时用铝较少,成本低
(4)当易拉罐底面半径在1.6~2.8cm变化时,用铝量随半径的增大而减小,当易拉罐底面半径在2.8~4.0cm间变化时,用铝量随半径的增大而增大.21·cn·jy·com
考点2、函数及其表示方式
1.(2014秋?太原期中)下列图象不能表示变量y是变量x的函数的是( )
A. B. C. D.
【解答】解:A、对于x的每一个取值,y都有唯一确定的值,故A正确;
B、对于x的每一个取值,y有不唯一确定的值,故B错误;
C、对于x的每一个取值,y都有唯一确定的值,故C正确;
D、对于x的每一个取值,y都有唯一确定的值,故D正确;
故选:B.
2.(2015秋?青岛校级期末)下列变量之间的关系:
(1)凸多边形的对角线条数与边数;
(2)三角形面积与它的底边(高为定值);
(3)x﹣y=3中的x与y;
(4)圆的面积与圆的半径;
(5)y=|x|中的x与y.
其中成函数关系的有( )
A.2个 B.3个 C.4个 D.5个
【解答】解:(1)凸多边形的对角线条数与边数是函数关系;
(2)三角形面积与它的底边(高为定值)是函数关系;
(3)x﹣y=3中的x与y是函数关系;
(4)圆的面积与圆的半径是函数关系;
(5)y=|x|中的x与y是函数关系;
故选:D..
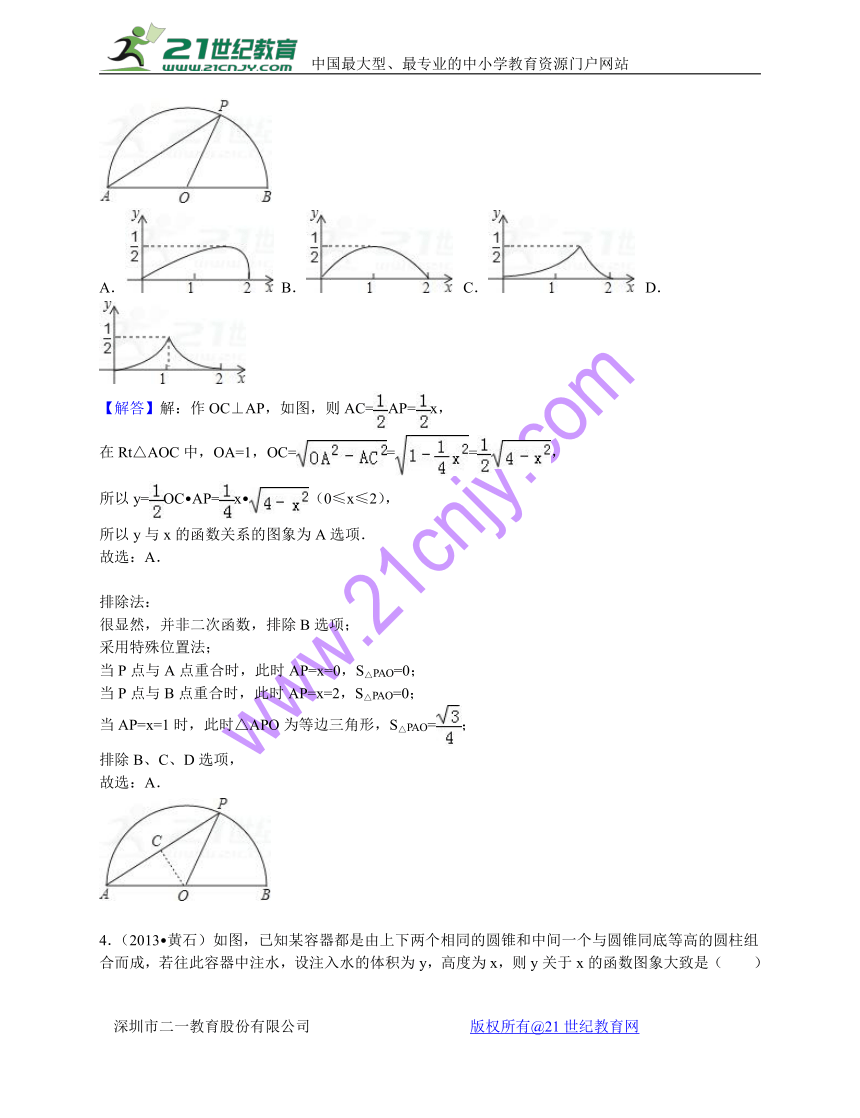
3.(2013?北京)如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2.设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. B. C. D.
【解答】解:作OC⊥AP,如图,则AC=AP=x,
在Rt△AOC中,OA=1,OC===,
所以y=OC?AP=x?(0≤x≤2),
所以y与x的函数关系的图象为A选项.
故选:A.
排除法:
很显然,并非二次函数,排除B选项;
采用特殊位置法;
当P点与A点重合时,此时AP=x=0,S△PAO=0;
当P点与B点重合时,此时AP=x=2,S△PAO=0;
当AP=x=1时,此时△APO为等边三角形,S△PAO=;
排除B、C、D选项,
故选:A.
4.(2013?黄石)如图,已知某容器都是由上下两个相同的圆锥和中间一个与圆锥同底等高的圆柱组合而成,若往此容器中注水,设注入水的体积为y,高度为x,则y关于x的函数图象大致是( )
A. B. C. D.
【解答】解:如图,①水在下边的圆锥体内时,水面的半径为xtanα,
水的体积y=π(xtanα)2?x=πtan2α?x3,
所以,y与x成立方关系变化,即小于直线增长;
②水面在圆柱体内时,y是x的一次函数;
③水在上边的圆锥体时,水的高度增长的速度与①中相反,即直线变缓了,
纵观各选项,只有A选项符合.
故选A.
5.(2015?广元)如图,矩形ABCD中,AB=3,BC=4,点P从A点出发,按A→B→C的方向在AB和BC上移动.记PA=x,点D到直线PA的距离为y,则y关于x的函数大致图象是( )
A. B. C. D.
【解答】解:(1)当点P在AB上移动时,
点D到直线PA的距离为:
y=DA=BC=4(0≤x≤3).
(2)如图1,当点P在BC上移动时,,
∵AB=3,BC=4,
∴AC=,
∵∠PAB+∠DAE=90°,∠ADE+∠DAE=90°,
∴∠PAB=∠DAE,
在△PAB和△ADE中,
∴△PAB∽△ADE,
∴,
∴,
∴y=(3<x≤5).
综上,可得
y关于x的函数大致图象是:
.
故选:D.
6.(2015?烟台)如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
A. B. C. D.
【解答】解:如图1,CH是AB边上的高,与AB相交于点H,,
∵∠C=90°,∠BAC=30°,AB=8,
∴AC=AB×cos30°=8×=4,BC=AB×sin30°=8×=4,
∴CH=AC×,AH=,
(1)当0≤t≤2时,
S==t2;
(2)当2时,
S=﹣
=t2[t2﹣4t+12]
=2t﹣2
(3)当6<t≤8时,
S=[(t﹣2)?tan30°]×[6﹣(t﹣2)]×[(8﹣t)?tan60°]×(t﹣6)
=[]×[﹣t+2+6]×[﹣t]×(t﹣6)
=﹣t2+2t+4﹣t2﹣30
=﹣t2﹣26
综上,可得
S=
∴正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是A图象.
故选:A.
7.(2015?本溪)如图,在△ABC中,∠C=90°,点P是斜边AB的中点,点M从点C向点A匀速运动,点N从点B向点C匀速运动,已知两点同时出发,同时到达终点,连接PM、PN、MN,在整个运动过程中,△PMN的面积S与运动时间t的函数关系图象大致是( )
A. B. C. D.
【解答】解:如图1,连接CP,
,
∵点P是斜边AB的中点,
∴S△ACP=S△BCP=S△ABC,
出发时,S△PMN=S△BCP=S△ABC;
∵两点同时出发,同时到达终点,
∴点N到达BC的中点时,点M也到达AC的中点,
∴S△PMN=S△ABC;
结束时,S△PMN=S△ACP=S△ABC,
在整个运动过程中设BC=a,AC=b,
∴S=[ab﹣VN?t?﹣(a﹣VN?t)?VM?t﹣(b﹣VM?t)?]
=(ab﹣VNb?t﹣aVM?t+VNVM?t2﹣ab+aVM?t)
=VNVM?t2﹣(VNb+aVM)t+ab,
∴△MPN的面积大小变化情况是:先减小后增大,而且是以抛物线的方式变化,
∴△PMN的面积S与运动时间t的函数关系图象大致是:
.
故选:A.
8.(2014?徐州)如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为 y=﹣3x+18 .
【解答】解:∵点P沿边DA从点D开始向点A以1cm/s的速度移动;点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.
∴当Q到达B点,P在AD的中点时,△PAQ的面积最大是9cm2,设正方形的边长为acm,
∴×a×a=9,
解得a=6,即正方形的边长为6,
当Q点在BC上时,AP=6﹣x,△APQ的高为AB,
∴y=(6﹣x)×6,即y=﹣3x+18.
故答案为:y=﹣3x+18.
9.(2013?咸宁)“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 ①③④ .(把你认为正确说法的序号都填上)
【解答】解:根据图象可知:
龟兔再次赛跑的路程为1000米,故①正确;
兔子在乌龟跑了40分钟之后开始跑,故②错误;
乌龟在30﹣﹣40分钟时的路程为0,故这10分钟乌龟没有跑在休息,故③正确;
y1=20x﹣200(40≤x≤60),y2=100x﹣4000(40≤x≤50),当y1=y2时,兔子追上乌龟,
此时20x﹣200=100x﹣4000,
解得:x=47.5,
y1=y2=750米,即兔子在途中750米处追上乌龟,故④正确.
综上可得①③④正确.
故答案为:①③④.
10.(1999?哈尔滨)函数y=中,自变量x的取值范围是 x≥,且x≠2 .
【解答】解:2x﹣1≥0,x﹣2≠0,解得:x≥,且x≠2.
考点3、一次函数的概念
1.(2016春?潮南区期末)已知y=(m+1),如果y是x的正比例函数,则m的值为( )
A.1 B.﹣1 C.1,﹣1 D.0
【解答】解:由y=(m+1),如果y是x的正比例函数,得
,
解得m=1,
故选:A.
2.(2015秋?陕西校级期末)若y=(m﹣1)是正比例函数,则m的值为( )
A.1 B.﹣1 C.1或﹣1 D.或﹣
【解答】解:根据正比例函数的定义,可得2﹣m2=1,m﹣1≠0,∴m=﹣1.
故选B.
3.(2012?江西模拟)当m= 1或﹣5或 时,函数y=(m+5)x2m﹣1+7x﹣3(x≠0)是一个一次函数.
【解答】解:①,
解得:m=1
根据题意得:2m﹣1=1,
解得:m=1,
此时函数化简为y=13x﹣3.
②2m﹣1=0,
解得:m=,
此时函数化简为y=7x+2.5;
③m+5=0,
解得:m=﹣5,
此时函数化简为y=7x﹣3.
故答案为:1或﹣5或.
4.(1999?贵阳)已知y=(k﹣3)k2x﹣2k﹣2是正比例函数,则k= ﹣1 .
【解答】解:根据定义﹣2k﹣2=0,(k﹣3)k2≠0,
解得:k=﹣1,满足(k﹣3)k2≠0,
所以k=﹣1.
故填﹣1.
5.(2015春?大名县期末)要使y=(m﹣2)x|m﹣1|+3是关于x的一次函数,则m= 0 .
【解答】解:根据一次函数的定义可得:m﹣2≠0,|m﹣1|=1,
由|m﹣1|=1,解得:m=0或2,
又m﹣2≠0,m≠2,
∴m=0.
故答案为:0.
6.(2015?石家庄模拟)新定义[a,b]为一次函数(其中a≠0,且a,b为实数)的“关联数”,若“关联数”[3,m+2]所对应的一次函数是正比例函数,则关于x的方程+=1的解为 .
【解答】解:根据“关联数”[3,m+2]所对应的一次函数是正比例函数,
得到y=3x+m+2为正比例函数,即m+2=0,
解得:m=﹣2,
则分式方程为﹣=1,
去分母得:2﹣(x﹣1)=2(x﹣1),
去括号得:2﹣x+1=2x﹣2,
解得:x=,
经检验x=是分式方程的解.
故答案为:x=.
考点4、一次函数的图象与性质
1.(2016?福州校级模拟)函数y=|2x|的图象是( )
A. B. C. D.
【解答】解:函数y=|2x|,当x≥0时,y=2x;当x≤0时,y=﹣2x,
故图象C符合,
故选C
2.(2015春?温岭市期末)定义运算*为:a*b=如:1*(﹣2)=﹣1×(﹣2)=2,则函数y=2*x的图象大致是( )
A. B. C. D.
【解答】解:y=2※x=,
x>0时,图象是y=2x的正比例函数中y轴右侧的部分;x≤0时,图象是y=﹣2x的正比例函数中y左侧的部分,
故选:C.
3.(1998?广东)已知y是x的函数,y与x﹣1成正比例,如果这个函数的图象经过点(a,a)(a≠0),那么它的图象大致是( )
A. B. C. D.
【解答】解:∵y与x﹣1成正比例,
∴y=k(x﹣1)(k≠0),
当x=1时,y=0,与k值无关,
∴直线y=k(x﹣1)经过定点(1,0),
∵点(a,a)(a≠0),
∴点(a,a)在第一三象限的平分线上,
∴直线的大致图象为B选项图象.
故选B.
4.(2015春?和平区期末)如图,两个不同的一次函数y=ax+b与y=bx+a的图象在同一平面直角坐标系的位置可能是( )
A. B. C. D.
【解答】解:A、若经过第一、二、三象限的直线为y=ax+b,则a>0,b>0,所以直线y=bx+a经过第一、二、三象限,所以A选项错误;
B、若经过第一、二、四象限的直线为y=ax+b,则a<0,b>0,所以直线y=bx+a经过第一、三、四象限,所以B选项错误;
C、若经过第一、三、四象限的直线为y=ax+b,则a>0,b<0,所以直线y=bx+a经过第一、二、四象限,所以C选项正确;
D、若经过第一、二、三象限的直线为y=ax+b,则a>0,b>0,所以直线y=bx+a经过第一、二、三象限,所以D选项错误;
故选C.
5.(2015秋?西安校级期末)直线y=kx+b经过一、三、四象限,则直线y=bx﹣k的图象只能是图中的( )
A. B. C. D.
【解答】解:∵直线y=kx+b经过第一、三、四象限,
∴k>0,b<0,
∴﹣k<0,
∴直线y=bx﹣k经过第二、三、四象限.
故选C.
6.(2013秋?南京期末)在同一平面直角坐标中,关于下列函数:①y=x+1;②y=2x+1;③y=2x﹣1;④y=﹣2x+1的图象,说法不正确的是( )
A.②和③的图象相互平行
B.②的图象可由③的图象平移得到
C.①和④的图象关于y轴对称
D.③和④的图象关于x轴对称
【解答】解:由题意得:y=2x+1与y=2x﹣1比例系数相等;y=2x﹣1与y=﹣2x+1的比例系数互为相反数,
所以②和③的图象相互平行,③和④的图象关于x轴对称,
故A、B、D正确,C错误,
故选C.
7.(2006?贵阳)函数y1=x+1与y2=ax+b的图象如图所示,这两个函数的交点在y轴上,那么y1、y2的值都大于零的x的取值范围是 ﹣1<x<2 .
【解答】解:根据图示及数据可知,
函数y1=x+1与x轴的交点坐标是(﹣1,0),
由图可知y2=ax+b与x轴的交点坐标是(2,0),
所以y1、y2的值都大于零的x的取值范围是:﹣1<x<2.
8.(2006?西岗区)如图是一次函数y1=ax+b,y2=kx+c的图象,观察图象,写出同时满足y1≥0,y2≥0时x的取值范围 ﹣2≤x≤1 .
【解答】解:根据图象和图中数据可知,同时满足y1≥0,y2≥0时,
x的取值范围﹣2≤x≤1.
9.(2012春?丘北县校级期中)如图,已知函数y=2x﹣5,观察图象回答下列问题:
(1)x <2.5 时,y<0;
(2)y <﹣5 时,x<0.
【解答】解:(1)∵当x<2.5时函数的图象在x轴的下方,
∴x<2.5时,y<0;
(2)∵当y<﹣5时函数图象在y轴的右侧,
∴y<﹣5时,x<0.
故答案为:<2.5,<﹣5.
10.作函数y=2x﹣4的图象,并根据图象回答下列问题.
(1)当﹣2≤x≤4,求函数y的取值范围.
(2)当x取何值时,y<0?y=0?y>0?
【解答】解:当x=0时,y=﹣4;
当y=0时,2x﹣4=0,
解得x=2,
∴函数图象与两坐标轴的交点为(0,﹣4)(2,0).
图象如下:
(1)x=﹣2时,y=2×(﹣2)﹣4=﹣8,
x=4时,y=2×4﹣4=4,
∵k=2>0,
∴y随x的增大而增大,
∴﹣8≤y≤4;
(2)x<2时,y<0;
x=2时,y=0;
x>2时,y>0.
考点5、一次函数的性质
1.(2015春?武平县校级月考)对于y=k2x(k≠0)的图象下列说法不正确的是( )
A.是一条直线 B.过点(,k)
C.经过一、三象限或二、四象限 D.y随x增大而增大
【解答】解:∵y=k2x(k≠0),
∴k2>0.
∴y=k2x(k≠0)的图象是正比例函数的图象,图象在第一、三象限,y随x的增大而增大,图象是一条直线.
当x=时,y=k2x=.
即y=k2x(k≠0)的图象过点().
由上可得,选项A的说法正确,选项B的说法正确,选项C的说法不正确,选项D的说法正确.
故选C.
2.(2011?黑龙江模拟)已知四条直线y=kx﹣3,y=﹣1,y=3和x=1所围成的四边形的面积是12,则k的值为( )
A.1或2 B.1或﹣2 C.﹣1或2 D.﹣1或﹣2
【解答】解:如图所示,根据题意,得
A(1,3),B(1,﹣1),C(,﹣1),D(,3).
显然ABCD是梯形,且梯形的高是4,根据梯形的面积是12,则梯形的上下底的和是6,则有
①当k<0时,1﹣+1﹣=6,
∴2﹣=6,
∴=﹣4,
解得k=﹣2;
②当k>0时,﹣1+﹣1=6,
∴=8,
解得k=1.
综上所述,则k=﹣2或1.
故选B.
3.(2016?江西校级模拟)设0<k<2,关于x的一次函数y=kx+2(1﹣x),当1≤x≤2时的最大值是( )
A.2k﹣2 B.k﹣1 C.k D.k+1
【解答】解:原式可以化为:y=(k﹣2)x+2,
∵0<k<2,
∴k﹣2<0,则函数值随x的增大而减小.
∴当x=1时,函数值最大,最大值是:(k﹣2)+2=k.
故选:C.
4.(2014?余姚市校级自主招生)对每个x,y是y1=2x,y2=x+2,y3=三个值中的最大值,则当x变化时,函数y的最小值为( )
A.4 B.6 C.8 D.
【解答】解:分别联立y1、y2,y1、y3,y2、y3,可知y1、y2的交点A(2,4);y1、y3的交点B(,);y2、y3的交点C(4,6),
∴当x≤2时,y最小=9;
当2<x≤时,y最小=;
当<x≤4时,y最小=;
当x>4时,y最小=8.
故选D.
5.(2012?上城区二模)已知四条直线y=kx﹣3,y=﹣1,y=3和x=1所围成的四边形的面积是8,则k的值为( )
A.或﹣4 B.或4 C.或﹣2 D.2或﹣2
【解答】解:∵y=﹣1,y=3,
∴围成的四边形是梯形,
直线y=﹣1,y=3之间的距离为3﹣(﹣1)=3=1=4,
所以,梯形的高为4,
联立,解得,
联立,解得,
①交点在直线x=1的左侧时,(1﹣+1﹣)×4=8,
解得k=﹣4,
②交点在直线x=1的右侧时,(﹣1+﹣1)×4=8,
解得k=,
综上,k的值为或﹣4.
故选A.
6.(2016春?泗县期中)要使直线y=(2m﹣3)x+(3n+1)的图象经过一、二、四象限,则m与n的取值为( )
A.m>,n>﹣ B.m>3,n>﹣3 C.m<,n<﹣ D.m<,n>﹣
【解答】解:∵直线y=(2m﹣3)x+(3n+1)的图象经过一、二、四象限,
∴,解得.
故选D.
7.(2014秋?郑州期末)下图中表示一次函数y=mx+n与正比例函数y=nx(m,n是常数,且mn<0)图象的是( )
A. B. C. D.
【解答】解:A、根据图中正比例函数y=nx的图象知,n<0;∵m,n是常数,且mn<0,∴m>0,∴一次函数y=mx+n的图象经过第一、三、四象限;故本选项错误;
B、根据图中正比例函数y=nx的图象知,n>0;∵m,n是常数,且mn<0,∴m<0,∴一次函数y=mx+n的图象经过第一、二、四象限;故本选项正确;
C、根据图中正比例函数y=nx的图象知,n<0;∵m,n是常数,且mn<0,∴m>0,∴一次函数y=mx+n的图象经过第一、三、四象限;故本选项错误;
D、根据图中正比例函数y=nx的图象知,n>0;∵m,n是常数,且mn<0,∴m<0,∴一次函数y=mx+n的图象经过第一、二、四象限;故本选项错误;
故选B.
8.(2015秋?丹阳市校级月考)已知一次函数y=kx﹣1的图象不经过第二象限,则正比例函数y=(k+1)x必定经过第 一、三 象限.
【解答】解:∵一次函数y=kx﹣1的图象经过第一、三、四象限
∴k>0
∴k+1>0
∴正比例函数y=(k+1)x必定经过第一、三象限.
9.(2012?北海)如图,点A的坐标为(﹣1,0),点B在直线y=2x﹣4上运动,当线段AB最短时,点B的坐标是 (,﹣) .
【解答】解:设AB′解析式为y=kx+b,
∵AB′⊥BB′,BB′解析式为y=2x﹣4,k1×k2=﹣1,
∴2k=﹣1,
k=﹣,于是函数解析式为y=﹣x+b,
将A(﹣1,0)代入y=﹣x+b得,+b=0,b=﹣,
则函数解析式为y=﹣x﹣,
将两函数解析式组成方程组得,
,
解得,故B点坐标为(,﹣).
故答案为(,﹣).
10.(2012?麻城市校级自主招生)设直线kx+(k+1)y﹣1=0与坐标轴所构成的直角三角形的面积为Sk,则S1+S2+…+S2008= .
【解答】解:∵kx+(k+1)y﹣1=0
∴当x=0时,y=;当y=0时,x=
∴Sk=××=,
根据公式可知,S1+S2+…+S2008=[﹣+﹣+…+﹣]=(1﹣)=.
11.(1998?大连)已知一次函数,若y随x的增大而减小,则m的值为 .
【解答】解:∵函数是一次函数,
∴
解得:m=﹣,
故答案为:.
12.(2014?自贡)一次函数y=kx+b,当1≤x≤4时,3≤y≤6,则的值是 2或﹣7 .
【解答】解:当k>0时,此函数是增函数,
∵当1≤x≤4时,3≤y≤6,
∴当x=1时,y=3;当x=4时,y=6,
∴,解得,
∴=2;
当k<0时,此函数是减函数,
∵当1≤x≤4时,3≤y≤6,
∴当x=1时,y=6;当x=4时,y=3,
∴,解得,
∴=﹣7.
故答案为:2或﹣7.
13.已知一次函数y=(m﹣1)+m的图象经过第二、三、四象限,则m的值是 ﹣ .
【解答】解:若一次函数y=(m﹣1)+m的图象经过第二、三、四象限,
则得到,
解得m=﹣.
14.(2014?梅州)已知直线y=kx+b,若k+b=﹣5,kb=6,那么该直线不经过第 一 象限.
【解答】解:∵k+b=﹣5,kb=6,
∴k<0,b<0,
∴直线y=kx+b经过二、三、四象限,即不经过第一象限.
故答案为:一.
15.(2015春?巴南区校级期末)已知函数y=(2m﹣2)x+m+1,
(1)m为何值时,图象过原点.
(2)已知y随x增大而增大,求m的取值范围.
(3)函数图象与y轴交点在x轴上方,求m取值范围.
(4)图象过二、一、四象限,求m的取值范围.
【解答】解:(1)∵函数图象过原点,
∴m+1=0,即m=﹣1;
(2)∵y随x增大而增大,
∴2m﹣2>0,解得m>1;
(3)∵函数图象与y轴交点在x轴上方,
∴m+1>0,即m>﹣1;
(4)∵图象过二、一、四象限,
∴,解得﹣1<m<1.
16.(2015秋?当涂县校级期中)已知一次函数y=(4﹣k)x﹣2k2+32
(1)k为何值时,y随x的增大而减小?
(2)k为何值时,它的图象经过原点?
【解答】解:(1)∵一次函数y=(4﹣k)x﹣2k2+32,y随x的增大而减小,
∴4﹣k<0
∴k>4;
(2)∵一次函数y=(4﹣k)x﹣2k2+32,它的图象经过原点,
∴﹣2k2+32=0
解得:k=±4
∵4﹣k≠0
∴k=﹣4.
考点6、一次函数的应用
1.小丽一家利用元旦三天驾车到某景点旅游。小汽车出发前油箱有油36L,行驶若干小时后,途中在加油站加油若干升。油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示。根据图象回答下列问题:
(1)小汽车行驶________h后加油, 中途加油__________L;
(2)求加油前油箱余油量Q与行驶时间t的函数关系式;
(3)如果加油站距景点200km,车速为80km/h,要到达目
的地,油箱中的油是否够用?请说明理由.
解:(1)3 ; 24
(2)设Q与t的函数关系式:Q=kt+b过(0、36),(3、6)
b=36
6=3k+b
k=-1
b=36
Q与t的函数关系式为:Q=-10t+36
(3)够用
到达目的地的时间t:200÷80=2.5(h)
需要油量: 2.5×10=25(L)
余油量30升 25<30
油箱中的油够用
2.在一次远足活动中,某班学生分成两组,第一组由甲地匀速步行到乙地后原路返回,第二组由甲地匀速步行经乙地继续前行到丙地后原路返回,两组同时出发,设步行的时间为t(h),两组离乙地的距离分别为S1(km)和S2(km),图中的折线分别表示S1、S2与t之间的函数关系.
(1)甲、乙两地之间的距离为 km,乙、丙两地之间的距离为 km;
(2)求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少?
(3)求图中线段AB所表示的S2与t间的函数关系式,并写出自变量t的取值范围.
解(1)8,2
(2)第二组由甲地出发首次到达乙地所用的时间为:[来源:Zxxk.Com]
(小时)
第二组由乙地到达丙地所用的时间为:
(小时)
(3)根据题意得A、B的坐标分别为(0.8,0)
和(1,2),设线段AB的函数关系式为:
,根据题意得:
解得:
∴图中线段AB所表示的S2与t间的函数关系式为:,自变量t的取值范围是:.
3.鞋子的“鞋码”和鞋长(cm)存在一种换算关系,下表是几组“鞋码”与鞋长换算的对应数值:[注:“鞋码”是表示鞋子大小的一种号码]
鞋长(cm)
16
19
21
24
鞋码(号)
22
28
32
38
(1)设鞋长为x,“鞋码”为y,试判断点(x,y)在你学过的哪种函数的图象上?
(2)求x、y之间的函数关系式;
(3)如果某人穿44号“鞋码”的鞋,那么他的鞋长是多少?
、解:(1)一次函数.
(2)设.
由题意,得
解得
∴.(x是一些不连续的值.一般情况下,x取16、16.5、17、17.5、…、26、26.5、27等)
(3)时,.
答:此人的鞋长为27cm.
4.某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件,可获利润150元,每制造一个乙种零件可获利润260元,在这20名工人中,车间每天安排x名工人制造甲种零件,其余工人制造乙种零件.
(1)请写出此车间每天所获利润y(元)与x(人)之间的函数关系式;
(2)若要使车间每天所获利润不低于24000元,你认为至少要派多少名工人去制造乙种零件才合适?
解:(1)此车间每天所获利润y(元)与x(人)之间的函数关系式是
y=6x·150+5(20-x)·260=26000-400x(0≤x≤20).
(2)当y≥24000时,有26000-400x≥24000,
∴x≤5,
∴20-x≥15.
∴要想使每天车间所获利润不低于24000元,至少要派15名工人去制造乙种零件才合适。
5.光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,现将这50台收割机派往A,B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见下表.
?
每台甲型收割机的租金
每台乙型收割机的租金
A地区
1800元
1600元
B地区
1600元
1200元
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x之间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分派方案,并将各种方案设计出来;
(1)派往A地区x台乙型联合收割机,则派往A地区(30-x)台甲型联合收割机,派往B地区(30-x)台乙型联合收割机,派往B地区20-(30-x)=x-10(台)甲型联合收割机.
∴y=1600x+120O(30-x)+180O(30-x)+1600(x-10)=20Ox+74000.
自变量x的取值范围是10≤x≤30(x是正整数),
(2)由题意得20Ox+74000≥7960O,∴x≥28.
∴x=28,29,30.
∴有3种不同分配方案.
①当x=28时,即派往A地区甲型联合收割机2台,乙型联合收割机28台,派往B地区甲型联合收割机18台,乙型联合收割机2台.
②当x=29时,即派往A地区甲型联合收割机1台,乙型联合收割机29台,派往B地区甲型联合收割机19台,乙型联合收割机1台.[来源:学科网ZXXK]
③当x=30时,即30台乙型联合收割机全部派往A地区,20台甲型联合收割机全部派往B地区.
6.辽南素有“苹果之乡”美称,某乡组织20辆汽车装运A、B、C三种苹果42吨到外地销售,按规定每辆车只装同一种苹果,且必须装满,每种苹果不少于2车。(1)设有x辆车装A种苹果,用y辆车装B种苹果,根据下表提供的信息求y与x的函数关系式,并求x的取值范围。
苹果的品种
A
B
C
每辆车运载量(吨)
2.2
2.1
2
每吨苹果获利(百元)
6
8
5
(2)设此次外销活动的利润为W(百元),求W与x的函数关系式及最大利润,并安排相应的车辆分配方案。
解:(1)由题意得,运C种苹果有(20-x-y)辆车,则2.2x+2.1y+2·(20-x-y)=42
∴y=-2x+20
∴运A种苹果有x辆汽车,运B种苹果有(-2x+20)辆汽车,运C种苹果有20-x-y=20-x-(20-2x)=x辆汽车
∴x为整数
∴x的取值范围是2≤x≤9,且x为整数
(2)W=2.2×6x+2.1×8(20-2x)+2×5x
∴W=-10.4x+336,∴-10.4<0,∴W随x的增大而减小,当x=2时,W有最大值为315.2,即最大利润为31520元。
二、课堂重难点题型精讲
题型1、一次函数的解析式
1.(2009?鄂州校级模拟)如图,已知点A的坐标为(0,1),点B的坐标为(,﹣2),点P在直线y=﹣x上运动,当|PA﹣PB|最大时点P的坐标为( )
A.(2,﹣2) B.(4,﹣4) C.(,﹣) D.(5,﹣5)
【解答】解:作A关于直线y=﹣x对称点C,易得C的坐标为(﹣1,0);连接BC,可得直线BC的方程为y=﹣x﹣;
求BC与直线y=﹣x的交点,可得交点坐标为(4,﹣4);
此时|PA﹣PB|=|PC﹣PB|=BC取得最大值,其他B C P不共线的情况,根据三角形三边的关系可得|PC﹣PB|<BC;
故答案为B.
2.(2012?洪山区校级模拟)已知点A(2a﹣1,3a+1),直线l经过点A,则直线l的解析式是 y=x+ .
【解答】解:∵点A的坐标为A(2a﹣1,3a+1),
∴,
由①得,a=,
由②得,a=,
所以=,
整理得,y=x+.
故答案为:y=x+.
3.(2005?黑龙江)一次函数y=kx+3的图象与坐标轴的两个交点之间的距离为5,则k的值为 或 .
【解答】解:在y=kx+3中令x=0,得y=3,
则函数与y轴的交点坐标是:(0,3);
设函数与x轴的交点坐标是(a,0),
根据勾股定理得到a2+32=25,
解得a=±4;
当a=4时,把(4,0)代入y=kx+3,得k=﹣;
当a=﹣4时,把(﹣4,0)代入y=kx+3,得k=.
故k的值为或.
4.(2011?辽阳)甲、乙两名自行车爱好者准备在一段长为3 500米的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面.他们同时出发,匀速前进,已知甲的速度为12米/秒,设甲、乙两人之间的距离为s(米),比赛时间为t(秒),图中的折线表示从两人出发至其中一人先到达终点的过程中s(米)与t(秒)的函数关系.根据图中信息,回答下列问题:
(1)乙的速度为 14 米/秒;
(2)当乙追上甲时,求乙距起点多少米.
(3)求线段BC所在直线的函数关系式.
【解答】解:(1)设乙的速度为x米/秒,
则300+150×12=150x,解得x=14,
故答案为:14;
(2)由图象可知乙用了150秒追上甲,
14×150=2 100(米).
∴当乙追上甲时,乙距起点2 100米;
(3)乙从出发到终点的时间为=250(秒),
此时甲、乙的距离为:
(250﹣150)(14﹣12)=200(米),
∴C点(250,200),
又B点坐标(150,0),
设BC所在直线的函数关系式为s=kt+b(k≠0,k,b为常数),
将B、C两点代入,得,解得,
∴BC所在直线的函数关系式为s=2t﹣300.
5.(2014春?武侯区校级月考)已知:一次函数y=kx+b的函数值随x的增大而减少,若已知自变量x的取值范围是﹣1≤x≤1,相应的函数值的取值范围是﹣3≤y≤﹣1,求函数解析式.
【解答】解:当k<0时,y随x的增大而减小,
把x=﹣1,y=﹣1;x=1,y=﹣3代入的解析式y=kx+b,
得
解得
∴一次函数解析式为y=﹣x﹣2.
题型2、一次函数图象上点的坐标的特征
1.(2012?巴中校级自主招生)如果一条直线l经过不同的三点A(a,b),B(b,a),C(a﹣b,b﹣a),那么直线l经过( )
A.第二、四象限 B.第一、二、三象限
C.第二、三、四象限 D.第一、三、四象限
【解答】解:设直线的解析式是y=kx+c,
把A(a,b),B(b,a),C(a﹣b,b﹣a)代入得:,
解得:k=﹣1,c=0,
∴y=﹣x,
∴图象经过第二、四象限,
故选A.
2.(2014?内江)如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、A2B3、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )
A. B. C. D.
【解答】解:∵A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,
∴依题意得:B1(1,2),B2(2,4),B3(3,6),…,Bn(n,2n)
∵A1B1∥A2B2,
∴△A1B1P1∽△A2B2P1,
∴=,
∴△A1B1P1与△A2B2P1对应高的比为:1:2,
∵A1A2=1,
∴A1B1边上的高为:,
∴=××2=,
同理可得:=,=,
∴Sn=.
故选:D.
3.(2013?江干区一模)已知两直线y1=kx+k﹣1、y2=(k+1)x+k(k为正整数),设这两条直线与x轴所围成的三角形的面积为Sk,则S1+S2+S3+…+S2013的值是( )
A. B. C. D.
【解答】解:∵方程组的解为,
∴两直线的交点是(﹣1,﹣1),
∵直线y1=kx+k﹣1与x轴的交点为(,0),y2=(k+1)x+k与x轴的交点为(,0),
∴Sk=×|﹣1|×|﹣|=|﹣|,
∴S1+S2+S3+…+S2013=×(1﹣+﹣+﹣+…+﹣)
=×(1﹣)
=×
=.
故选D.
4.(2015?宁德)如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2015的坐标是( )
A.(22014,22014) B.(22015,22015) C.(22014,22015) D.(22015,22014)
【解答】解:∵OA1=1,
∴点A1的坐标为(1,0),
∵△OA1B1是等腰直角三角形,
∴A1B1=1,
∴B1(1,1),
∵△B1A1A2是等腰直角三角形,
∴A1A2=1,B1A2=,
∵△B2B1A2为等腰直角三角形,
∴A2A3=2,
∴B2(2,2),
同理可得,B3(22,22),B4(23,23),…Bn(2n﹣1,2n﹣1),
∴点B2015的坐标是(22014,22014).
故选:A.
5.(2016春?秦皇岛期末)已知直线y=2x+8与x轴和y轴的交点的坐标分别是 (﹣4,0) 、 (0,8) ;与两条坐标轴围成的三角形的面积是 16 .
【解答】解:当y=0时,x=﹣4,
∴直线y=2x+8与x轴的交点坐标为(﹣4,0);
当x=0时,y=8,
∴直线y=2x+8与y轴的交点坐标为(0,8);
∴三角形的底是|﹣4|,高是8,
∴与两条坐标轴围成的三角形的面积是×|﹣4|×8=16.
故填(﹣4,0)、(0,8)、16.
6.(2013?广安)已知直线y=x+(n为正整数)与坐标轴围成的三角形的面积为Sn,则S1+S2+S3+…+S2012= .
【解答】解:令x=0,则y=,
令y=0,则﹣x+=0,
解得x=,
所以,Sn=??=(﹣),
所以,S1+S2+S3+…+S2012=(﹣+﹣+﹣+…+﹣)=(﹣)=.
故答案为:.
7.(2012?南通)无论a取什么实数,点P(a﹣1,2a﹣3)都在直线l上.Q(m,n)是直线l上的点,则(2m﹣n+3)2的值等于 16 .
【解答】解:∵令a=0,则P(﹣1,﹣3);再令a=1,则P(0,﹣1),由于a不论为何值此点均在直线l上,
∴设此直线的解析式为y=kx+b(k≠0),
∴,解得,
∴此直线的解析式为:y=2x﹣1,
∵Q(m,n)是直线l上的点,
∴2m﹣1=n,即2m﹣n=1,
∴原式=(1+3)2=16.
故答案为:16.
8.(2009?株洲)孔明同学在解方程组的过程中,错把b看成了6,他其余的解题过程没有出错,解得此方程组的解为,又已知直线y=kx+b过点(3,1),则b的正确值应该是 ﹣11 .
【解答】解:依题意将代入y=kx+6
得:2=﹣k+6,k=4;
将点(3,1)和k=4代入y=kx+b
得1=3×4+b,
∴b=﹣11.
9.(2015?东营)如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标是 (,) .
【解答】解:过B1向x轴作垂线B1C,垂足为C,
由题意可得:A(1,0),AO∥A1B1,∠B1OC=30°,
∴CB1=OB1cos30°=,
∴B1的横坐标为:,则B1的纵坐标为:,
∴点B1,B2,B3,…都在直线y=x上,
∴B1(,),
同理可得出:A的横坐标为:1,
∴y=,
∴A2(2,),
…
An(1+,).
∴A2015(,).
故答案为(,).
10.(2015?丹东)如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1A2B1、△A2A3B2、△A3A4B3…△AnAn+1Bn均为等边三角形,点A1、A2、A3…An+1在x轴的正半轴上依次排列,点B1、B2、B3…Bn在直线OD上依次排列,那么点Bn的坐标为 (3×2n﹣2,×2n﹣2) .
【解答】解:∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,
∵∠B1OA2=30°,
∴∠B1OA2=∠A1B1O=30°,可求得OA2=2OA1=2,
同理可求得OAn=2n﹣1,
∵∠BnOAn+1=30°,∠BnAnAn+1=60°,
∴∠BnOAn+1=∠OBnAn=30°
∴BnAn=OAn=2n﹣1,
即△AnBnAn+1的边长为2n﹣1,则可求得其高为×2n﹣1=×2n﹣2,
∴点Bn的横坐标为×2n﹣1+2n﹣1=×2n﹣1=3×2n﹣2,
∴点Bn的坐标为(3×2n﹣2,×2n﹣2).
故答案为(3×2n﹣2,×2n﹣2).
11.(2015?衡阳)如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA1=1,则OA2015的长为 22014 .
【解答】解:因为OA1=1,
∴OA2=2,OA3=4,OA4=8,
由此得出OAn=2n﹣1,
所以OA2015=22014,
故答案为:22014.
12.(2015?北海)如图,直线y=﹣2x+2与两坐标轴分别交于A、B两点,将线段OA分成n等份,分点分别为P1,P2,P3,…,Pn﹣1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn﹣1,用S1,S2,S3,…,Sn﹣1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn﹣1Pn﹣2Pn﹣1的面积,则当n=2015时,S1+S2+S3+…+Sn﹣1= .
【解答】解:∵P1,P2,P3,…,Pn﹣1是x轴上的点,且OP1=P1P2=P2P3=…=Pn﹣2Pn﹣1=,
分别过点p1、p2、p3、…、pn﹣2、pn﹣1作x轴的垂线交直线y=﹣2x+2于点T1,T2,T3,…,Tn﹣1,
∴T1的横坐标为:,纵坐标为:2﹣,
∴S1=×(2﹣)=(1﹣)
同理可得:T2的横坐标为:,纵坐标为:2﹣,
∴S2=(1﹣),
T3的横坐标为:,纵坐标为:2﹣,
S3=(1﹣)
…
Sn﹣1=(1﹣)
∴S1+S2+S3+…+Sn﹣1=[n﹣1﹣(n﹣1)]=×(n﹣1)=,
∵n=2015,
∴S1+S2+S3+…+S2014=××2014=.
故答案为:.
13.(2006?绍兴)如图,一次函数y=x+5的图象经过点P(a,b)和Q(c,d),则a(c﹣d)﹣b(c﹣d)的值为 25 .
【解答】解:由P(a,b),Q(c,d)两点在一次函数y=x+5的图象上,
则b=a+5,d=c+5,即:a﹣b=﹣5,c﹣d=﹣5.
所以a(c﹣d)﹣b(c﹣d)=(c﹣d)(a﹣b)=(﹣5)×(﹣5)=25.
14.(2016?鄂州)如图,直线l:y=﹣x,点A1坐标为(﹣3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2016的坐标为 (﹣,0) .
【解答】解:∵点A1坐标为(﹣3,0),
∴OA1=3,
∵在y=﹣x中,当x=﹣3时,y=4,即B1点的坐标为(﹣3,4),
∴由勾股定理可得OB1==5,即OA2=5=3×,
同理可得,
OB2=,即OA3==5×()1,
OB3=,即OA4==5×()2,
以此类推,
OAn=5×()n﹣2=,
即点An坐标为(﹣,0),
当n=2016时,点A2016坐标为(﹣,0).
故答案为:(﹣,0)
15.(2014?高青县模拟)直线y=x+2与x轴、y轴分别交于A、B两点,D是x轴上一点,坐标为(x,0),△ABD的面积为S.
(1)求点A和点B的坐标;
(2)求S与x的函数关系式;
(3)当S=12时,求点D的坐标.
【解答】解:(1)令y=0,则x+2=0,解得x=﹣4,
令x=0,则y=2,
所以,点A,B的坐标分别为(﹣4,0)和(0,2);
(2)∵A(﹣4,0),D(x,0),
∴AD=|x﹣(﹣4)|,
∴S=AD?OB=|x﹣(﹣4)|×2=|x+4|;
(3)∵S=12,
∴|x+4|=12,
即x+4=12或x+4=﹣12,
解得x=8或x=﹣16,
所以,D的坐标为(8,0)或(﹣16,0).
16.(2015春?自贡期末)点P(x,y)在直线x+y=8上,且x>0,y>0,点A的坐标为A(6,0),设△OPA的面积为S.
(1)求S与x的函数关系式,并直接写出x的取值范围;
(2)当S=9时,求点P的坐标.
【解答】解:(1)过点P作PB⊥x轴,垂足为B,
由三角形的面积公式可知:S==即:s=﹣3x+24.(0<x<8);
(2)将s=9代入s=﹣3x+24得:x=5,将x=5代入x+y=8得:y=3,
故点P的坐标为(5,3).
题型3、一次函数图象的几何变换
1.(2016春?云梦县期末)如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x﹣5上时,线段BC扫过的面积为( )
A.80 B.88 C.96 D.100
【解答】解:∵点A、B的坐标分别为(2,0)、(8,0),
∴AB=6,
∵∠CAB=90°,BC=10,
∴CA==8,
∴C点纵坐标为:8,
∵将△ABC沿x轴向右平移,当点C落在直线y=x﹣5上时,
∴y=8时,8=x﹣5,
解得:x=13,
即A点向右平移13﹣2=11个单位,
∴线段BC扫过的面积为:11×8=88.
故选:B.
2.(2015?白云区校级一模)把函数y=﹣2x+3的图象向左平移2个单位长度,再向下平移2个单位长度,可得到的图象的函数解析式是( )
A.y=﹣2x+7 B.y=﹣2x﹣7 C.y=﹣2x﹣3 D.y=﹣2x
【解答】解:把函数y=﹣2x+3的图象向左平移2个单位长度,再向下平移2个单位长度,可得到的图象的函数解析式是:y=﹣2(x+2)+3﹣2=﹣2x﹣3,
故选C.
3.(2010?黄石)将函数y=﹣6x的图象l1向上平移5个单位得直线l2,则直线l2与坐标轴围成的三角形面积为 .
【解答】解:由题意得l2的解析式为:y=﹣6x+5,
∴与y轴的交点为(0,5),
与x轴的交点为(,0),
∴所求三角形的面积=×5×=.
4.(2013?包头)如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D.若DB=DC,则直线CD的函数解析式为 y=﹣2x﹣2 .
【解答】解:设直线AB的解析式为y=kx+b,
把A(0,2)、点B(1,0)代入,得,
解得,
故直线AB的解析式为y=﹣2x+2;
将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D,使DB=DC,
∴DO垂直平分BC,
∴OC=OB,
∵直线CD由直线AB平移而成,
∴CD=AB,
∴点D的坐标为(0,﹣2),
∵平移后的图形与原图形平行,
∴平移以后的函数解析式为:y=﹣2x﹣2.
故答案为:y=﹣2x﹣2.
5.(2014秋?南京校级期末)如图,正比例函数y=kx(k≠0)的图象经过点A(2,4),AB⊥x轴于点B,将△ABO绕点A逆时针旋转90°得到△ADC,则直线AC的函数表达式为 y=﹣0.5x+5 .
【解答】解:∵正比例函数y=kx(k≠0)经过点A(2,4)
∴4=2k,
解得:k=2,
∴y=2x;
∵A(2,4),AB⊥x轴于点B,
∴OB=2,AB=4,
∵△ABO绕点A逆时针旋转90°得到△ADC,
∴DC=OB=2,AD=AB=4
∴C(6,2)
设直线AC的解析式为y=ax+b,
把(2,4)(6,2)代入解析式可得:,
解得:,
所以解析式为:y=﹣0.5x+5
6.(2011?咸宁)在平面直角坐标系中,点P从原点O出发,每次向上平移2个单位长度或向右平移1个单位长度.
(1)实验操作:
在平面直角坐标系中描出点P从点O出发,平移1次后,2次后,3次后可能到达的点,并把相应点的坐标填写在表格中:
P从点O出发平移次数
可能到达的点的坐标
1次
(0,2),(1,0)
2次
3次
(2)观察发现:
任一次平移,点P可能到达的点在我们学过的一种函数的图象上,如:平移1次后在函数 y=﹣2x+2 的图象上;平移2次后在函数 y=﹣2x+4 的图象上…由此我们知道,平移n次后在函数 y=﹣2x+2n 的图象上.(请填写相应的解析式)
(3)探索运用:
点P从点O出发经过n次平移后,到达直线y=x上的点Q,且平移的路径长不小于50,不超过56,求点Q的坐标.
【解答】解:(1)如图所示:
P从点O出发平移次数
可能到达的点
的坐标
1次
2次
(0,4),(1,2),(2,0)
3次
(0,6),(1,4),(2,2),(3,0)
(2)设过(0,2),(1,0)点的函数解析式为:y=kx+b(k≠0),
则,
解得,
故第一次平移后的函数解析式为:y=﹣2x+2;
∴答案依次为:y=﹣2x+2;y=﹣2x+4;y=﹣2x+2n.
(3)设点Q的坐标为(x,y),依题意,.
解这个方程组,得到点Q的坐标为.
∵平移的路径长为x+y,
∴50≤≤56.
∴37.5≤n≤42.
∵点Q的坐标为正整数,
∴n是3的倍数,n可以取39、42,
∴点Q的坐标为(26,26),(28,28).
7.(2010?顺义区二模)如图,在平面直角坐标系xOy中,A点的坐标为(1,2),B点的坐标为(2,1).
(1)求△OAB的面积;
(2)若△OAB沿直线向下平移,使点A落在x轴上,画出平移后的三角形,求平移的距离及平移过程中△OAB所扫过的面积.
【解答】解:(1)△OAB的面积等于正方形的面积﹣3个三角形的面积
=2×2﹣
=;
(2)
平移的距离=
△OAB所扫过的面积=2+=11.5.
8.(2014?六合区一模)已知一次函数y=x+b的图象与x轴,y轴交于点A、B.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b= 2 ;
(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值;
(3)当b>0时,函数y1=x+b图象绕点B逆时针旋转n°(0°<n°<180°)后,对应的函数关系式为
y=﹣x+b,求n的值.
【解答】解:(1)将y=x+b的图象沿x轴向右平移2个单位后得到y=x﹣2+b,
由题意,得0=0﹣2+b,
解得b=2.
故答案为2;
(2)∵当x=0时,y=4,
∴y2=kx+4图象与y轴交于点(0,4).
∵(0,4)关于y轴对称点就是本身,
∴(0,4)在函数y=x+b图象上.
∴b=4.
∴一次函数y1=x+4,它与x轴的交点坐标为(﹣4,0).
∵y2=kx﹣4的图象与y1=x+4的图象关于y轴对称,
∴y2=kx﹣4的图象经过点(4,0),则0=4k+4,
∴k=﹣1;
(3)∵当x=0时,y1=b,
∴y1=x+b图象与y轴交于点B(0,b).
∵当y1=0时,x=﹣b,
∴y1=x+b图象与x轴交于点A(﹣b,0).
如图,∵AO=BO=b(b>0),∴∠ABO=45°.
∵当y3=0时,x=,
∴y3=﹣x+b图象与x轴交于点C(,0).
如图,∵CO=,
∴tan∠ACB==,
∴∠ACB=60°.
∴n°=180°﹣∠ACB﹣∠BAC=75°.
即n的值为75.
题型4、一次函数与一元一次方程
1.(2015春?迁安市期末)如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则方程2x=ax+4的解集为( )
A.x= B.x=3 C.x=﹣ D.x=﹣3
【解答】解:∵A点在直线y=2x上,
∴3=2m,解得m=,
∴A点坐标为(,3),
∵y=2x,y=ax+4,
∴方程2x=ax+4的解即为两函数图象的交点横坐标,
∴方程2x=ax+4的解为x=,
故选A.
2.(2015秋?合肥校级期中)已知方程x+b=0的解是x=﹣2,下列可能为直线y=x+b的图象是( )
A. B. C. D.
【解答】解:∵方程x+b=0的解是x=﹣2,
∴直线y=x+b过点(﹣2,0),
∵直线y=x+b经过第一、三象限.
故选C.
3.(2014秋?常熟市校级期末)同一平面直角坐标系中,一次函数y=k1x+b的图象与一次函数y=k2x的图象如图所示,则关于x的方程k1x+b=k2x的解为( )
A.x=0 B.x=﹣1 C.x=﹣2 D.x=1
【解答】解:由函数图象,得两直线的交点坐标是(﹣1,﹣2),
k1x+b=k2x的解为x=﹣1,
故选:B.
4.(2014春?博白县期末)一次函数y=ax+b交x轴于点(﹣3,0),则关于x的方程ax+b=0的解是 x=﹣3 .
【解答】解:由题意可知:当x=﹣3时,函数值为0;
因此当x=﹣3时,ax+b=0,
即方程ax+b=0的解为:x=﹣3.
故答案为:x=﹣3.
5.(2014秋?淄川区期末)已知关于x的一元一次方程kx+b=0的解是x=﹣2,一次函数y=kx+b的图象与y轴交于点(0,2),则这个一次函数的表达式是 y=x+2 .
【解答】解:把x=﹣2代入kx+b=0得﹣2k+b=0,
把(0,2)代入y=kx+b得b=2,
所以﹣2k+2=0,解得k=1,
所以一次函数解析式为y=x+2.
故答案为y=x+2.
6.(2014秋?宁化县校级期中)一次函数y=kx+b(k≠0)中,x与y的部分对应值如下表
x
﹣2
﹣1
0
1
2
y
6
4
2
0
﹣2
那么,一元一次方程kx+b=0在这里的解为: x=1 .
【解答】解:根据上表中的数据值,当y=0时,x=1,
即一元一次方程kx+b=0的解是x=1.
故答案是:x=1.
7.(2014秋?海宁市校级月考)如图,直线l1:y=k1x+b与直线l2:y=k2x+c在同一平面直角坐标系中的图象如图所示,则关于x的方程k1x+b=k2x+c的解x= 1 .
【解答】解:∵直线y=k1x+b与直线y=k2x+c的交点坐标为(1,﹣2),
∴关于x的方程k1x+b=k2x+c的解为x=1.
故答案为1.
8.(2012?湖州)一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为 x=﹣1 .
【解答】解∵一次函数y=kx+b过(2,3),(0,1)点,
∴,
解得:,
一次函数的解析式为:y=x+1,
∵一次函数y=x+1的图象与x轴交于(﹣1,0)点,
∴关于x的方程kx+b=0的解为x=﹣1.
故答案为:x=﹣1.
9.(2012秋?滨海县期末)直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图,则关于x的方程:k1x+b=k2x的解为x= ﹣1 .
【解答】解:∵直线l1:y=k1x+b与直线l2:y=k2x交于点(﹣1,2),
∴关于x的方程:k1x+b=k2x的解为x=﹣1,
故答案为:﹣1.
10.(2014春?江西期末)如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:
(1)方程kx+b=0的解;
(2)式子k+b的值;
(3)方程kx+b=﹣3的解.
【解答】解:(1)如图所示,当y=0时,x=2.
故方程kx+b=0的解是x=2;
(2)根据图示知,该直线经过点(2,0)和点(0,﹣2),则
,
解得 ,
故k+b=1﹣2=﹣1,即k+b=﹣1;
(3)根据图示知,当y=﹣3时,x=﹣1.
故方程kx+b=﹣3的解是x=﹣1.
题型5、一次函数与二元一次方程组
1.(2012?南宁)如图,已知函数y=x﹣2和y=﹣2x+1的图象交于点P,根据图象可得方程组的解是 .
【解答】解:∵由图象可知:函数y=x﹣2和y=﹣2x+1的图象的交点P的坐标是(1,﹣1),
又∵由y=x﹣2,移项后得出x﹣y=2,
由y=﹣2x+1,移项后得出2x+y=1,
∴方程组的解是,
故答案为:.
2.(2013秋?平川区期末)如图,已知y=ax+b和y=kx的图象交于点P,根据图象可得关于x、y的二元一次方程组的解是 .
【解答】解:∵y=ax+b和y=kx的图象交于点P(﹣4,﹣2),
∴方程组的解是.
故答案为.
3.(2015秋?古田县月考)(1)求一次函y=2x﹣2的图象l1与y=x﹣1的图象l2的交点P的坐标.
(2)求直线l1与y轴交点A的坐标;求直线l2与x轴的交点B的坐标;
(3)求由三点P、A、B围成的三角形的面积.
【解答】解:(1)由解得:所以点P的坐标为(,﹣),
(2)当x=0时,由y=2×0﹣2=﹣2,所以点A坐标是(0,﹣2).
当y=0时,由0=﹣x﹣1,得x=2,所以点B坐标是(2,0).
(3)如图:连AB,
∴S△PAB=S△ABC﹣S△PBC=×2×1﹣××1=.
4.(2010秋?文成县校级期末)如图,L1,L2分别表示两个一次函数的图象,它们相交于点P,
(1)求出两条直线的函数关系式;
(2)点P的坐标可看作是哪个二元一次方程组的解;
(3)求出图中△APB的面积.
【解答】解:(1)设直线L1的解析式是y=kx+b,已知L1经过点(0,3),(1,0),
可得:,解得,
则函数的解析式是y=﹣3x+3;
同理可得L2的解析式是:y=x﹣2.
(2)点P的坐标可看作是二元一次方程组的解.
(3)易知:A(0,3),B(0,﹣2),P(,﹣);
∴S△APB=AB?|xP|=×5×=.
5.(2009?怀柔区二模)我们知道,在数轴上,x=1表示一个点,而在平面直角坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x﹣y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象,它也是一条直线,如图1.
观察图1可以得出:直线x=1与直线y=2x+1的交点P的坐标(1,3)就是
方程组的解,所以这个方程组的解为.
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它左侧的部分,如图②;y≤2x+1也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图3;
那么,所围成的区域就是图4中的阴影部分.
回答下列问题:
(1)在下面的直角坐标系中,用作图象的方法求出方程组的解;
(2)在右面的直角坐标系中用阴影表示,所围成的区域.
【解答】解:(1)在坐标系中分别作出直线x=2和直线,
这两条直线的交点是(2,0).
则x=2,y=0就是方程组的解.
(2)在(1)问的前提下作出y=﹣x2+2x+3的图象,
则所围成的区域如图阴影所示.
题型6、一次函数与一元一次不等式
1.(2013?潍坊二模)如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx﹣2的解集是( )
A.1<x<2 B.0<x<2 C.0<x<1 D.1<x
【解答】解:由于直线y1=kx+b过点A(0,2),P(1,m),
则有:,
解得 .
∴直线y1=(m﹣2)x+2.
故所求不等式组可化为:
mx>(m﹣2)x+2>mx﹣2,
不等号两边同时减去mx得,0>﹣2x+2>﹣2,
解得:1<x<2,
故选A.
2.(2015?黄冈中学自主招生)如图,表示阴影区域的不等式组为( )
A. B.
C. D.
【解答】解:∵x≥0表示直线x=0右侧的部分,2x+y≤5表示直线y=﹣2x+5左下方的部分,3x+4y≥9表示直线y=﹣x+右上方的部分,
故根据图形可知:满足阴影部分的不等式组为:.
故选D.
3.(2014春?通川区期末)如图,已知:函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是( )
A.x>﹣5 B.x>﹣2 C.x>﹣3 D.x<﹣2
【解答】解:∵函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),
则根据图象可得不等式3x+b>ax﹣3的解集是x>﹣2,
故选B.
4.(2011?鄂尔多斯)如图,直线y1=mx经过P(2,1)和Q(﹣4,﹣2)两点,且与直线y2=kx+b交于点P,则不等式kx+b>mx>﹣2的解集为 ﹣4<x<2 .
【解答】解:将P(2,1)代入解析式y1=mx得,1=2m,m=,
函数解析式为y=x,
将Q点纵坐标﹣2代入解析式得,﹣2=x,
x=﹣4,
则Q点坐标为(﹣4,﹣2).
kx+b>mx>﹣2的解集为y2>y1>﹣2时,x的取值范围为﹣4<x<2.
故答案为:﹣4<x<2.
5.(2015?甘南州)如图是一次函数的y=kx+b图象,则关于x的不等式kx+b>0的解集为 x>﹣2 .
【解答】解:由图可知:当x>﹣2时,y>0,即kx+b>0;
因此kx+b>0的解集为:x>﹣2.
6.(2015?德州校级二模)已知一次函数y=ax+b(a、b是常数,a≠0)函数图象经过(﹣1,4),(2,﹣2)两点,下面说法中:(1)a=2,b=2;(2)函数图象经过(1,0);(3)不等式ax+b>0的解集是x<1;(4)不等式ax+b<0的解集是x<1;正确的说法有 (2)(3) .(请写出所有正确说法的序号)
【解答】解:∵一次函数y=ax+b(a、b是常数,a≠0)函数图象经过(﹣1,4),(2,﹣2)两点,
∴,
解得a=﹣2,b=2,
∴一次函数的解析式为y=﹣2x+2,图象经过(1,0)点,
不等式﹣2x+b>0的解集为x<1,
不等式﹣2x+b<0的解集为x>1,
(1)错误.(2)正确,(3)正确,(4)错误.
故正确说法为(2)(3).
7.(2011?西宁)如图,直线y=kx+b经过A(﹣1,1)和B(﹣,0)两点,则关于x的不等式组0<kx+b<﹣x的解集为 ﹣<x<﹣1 .
【解答】解:∵直线y=kx+b经过B(﹣,0)点,
∴0<kx+b,就是y>0,y>0的范围在x轴的上方,
此时:﹣<x,
∵直线y=﹣x经过A(﹣1,1),
那么就是A点左侧kx+b<﹣x,
得:x<﹣1,
故不等式组0<kx+b<﹣x的解集为:﹣<x<﹣1.
故答案为:﹣<x<﹣1.
8.(2016春?十堰期末)如图所示,函数y=ax+b和y=|x|的图象相交于(﹣1,1),(2,2)两点.当y1>y2时,x的取值范围是 x<﹣1或x>2 .
【解答】解:∵函数y=ax+b和y=|x|的图象相交于(﹣1,1),(2,2)两点,
∴根据图象可以看出,当y1>y2时,x的取值范围是x>2或x<﹣1,
故答案为:x<﹣1或x>2.
9.(2015?辽宁校级模拟)如图所示,函数y1=|x|和y2=x+的图象相交于(﹣1,1),(2,2)两点.当y1>y2时,x的取值范围是 x<﹣1或x>2 .
【解答】解:当x≥0时,y1=x,又,
∴两直线的交点为(2,2),
y2=x+当x<0时,y1=﹣x,又y2=x+,
∴两直线的交点为(﹣1,1),
由图象可知:当y1>y2时x的取值范围为:x<﹣1或x>2.
故答案为:x<﹣1或x>2.
题型7、两直线的平行和相交问题
1.(2011?潮州校级模拟)直线y=﹣x+6和直线y=x﹣2与y轴围成的三角形的面积是( )
A.20 B.10 C.40 D.12
【解答】解:∵直线y=﹣x+6与y轴的交点为(0,6),直线y=x﹣2与y轴的交点分别为(0,﹣2),
∴两条直线与y轴交点之间距离为|6+2|=8,
由题意得,
解得,故两直线的交点坐标为(5,3),
∴两直线与y轴围成的三角形的面积=×8×5=20.
故选A.
2.已知直线y1=x,,,若无论x取何值,y总取y1、y2、y3中的最小值,则y的最大值为 .
【解答】解:如图,y的最小值在三条直线的公共部分所在的区域,∵y2与y3的交点最高,
∴y2=x+1,y3=﹣x+5的交点的y值最大,
联立得,,
解得,
∴y的最大值为.
故答案为:.
3.(2015?大连)在平面直角坐标系中,点A,B的坐标分别为(m,3),(3m﹣1,3),若线段AB与直线y=2x+1相交,则m的取值范围为 ≤m≤1 .
【解答】解:当y=3时,2x+1=3,解得x=1,
所以直线y=3与直线y=2x+1的交点为(1,3),
当点B在点A的右侧,则m≤1≤3m﹣1,解得≤m≤1;
当点B在点A的左侧,则3m﹣1≤1≤m,无解,
所以m的取值范围为≤m≤1.
4.(2004?西藏)已知,如图,直线y=8﹣2x与y轴交于点A,与x轴交于点B,直线y=x+b与y轴交于点C,与x轴交于点D,如果两直线交于点P,且AC:CO=3:5(AO>CO).
(1)求点A、B的坐标;
(2)求四边形COBP的面积S.
【解答】解:(1)∵直线y=8﹣2x与y轴交于点A,与x轴交于点B,
∴当x=0时,y=8﹣2×0=8,
当y=0时,x=4,
∴A(0,8),B(4,0);
(2)AC:CO=3:5,AO=8,
∴C(0,5),
∵直线y=x+b与y轴交于点C,
∴5=0+b,
b=5,
∴y=x+5,
,
解得:,
∴P(1,6),
∴四边形COBP的面积S=(5+6)×1+×3×6=.
5.(2015秋?沛县期末)如图,直线l1的函数表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
(1)图中点D的坐标为 (1,0) .
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上是否存在点P,使得△PDC的面积是△ADC面积的2倍?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【解答】解:(1)∵D在直线l1y=﹣3x+3的图象上,
∴当y=0时,0=﹣3x+3,
解得:x=1,
∴D(1,0),
故答案为:(1,0);
(2)设直线l2的解析表达式为y=kx+b,
∵过(3,﹣),(4,0),
∴,
解得,
∴直线l2的解析表达式为y=x﹣6;
(3)∵,解得:,
∴C(2,﹣3),
∴△ADC的面积为:×AD×3=×3×3=;
(4)存在,
∵△PDC的面积是△ADC面积的2倍,
∴△PDC的面积是9,
当P在第一象限时,△PDA面积为,
∴P点纵坐标为3,
∵P在直线l2上,
∴横坐标为6,
∴P(6,3);
当P在第三象限时,△DPA面积为,
∴P纵坐标为﹣9,
∵P在直线l2上,
∴横坐标为﹣2,
∴P(﹣2,﹣9);
综上:P(﹣2,﹣9)或(6,3).
6.(2015秋?深圳期末)如图,已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,与直线l2:y=﹣x交于点P.直线l3:y=﹣x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R.
(1)点A的坐标是 (﹣3,0) ,点B的坐标是 (0,3) ,点P的坐标是 (﹣2,1) ;
(2)将△POB沿y轴折叠后,点P的对应点为P′,试判断点P′是否在直线l3上,并说明理由;
(3)求△PQR的面积.
【解答】解:(1)∵直线l1:y=x+3与x轴交于点A,与y轴交于点B,
∴令y=0,求得x=﹣3,令x=0,求得y=3,
∴A(﹣3,0)、B(0,3),
∵直线l1与直线l2y=﹣x交于点P.
∴解得,
∴P(﹣2,1),
故答案为:(﹣3,0),(0,3),(﹣2,1);
(2)点P?在直线l3上
∵P(﹣2,1),且将△POB沿y轴折叠后,点P?与点P关于y轴对称,
∴P?(2,1),
当x=2时,代入y=﹣x+4得y=﹣×2+4=1,
∴点P?在直线l3上;
(3)分别过点P作PE⊥x轴于F,过点Q作QF⊥x轴于F,过点R作RG⊥x轴于G,
由 得,
∴Q(,),
由 得
∴R(4,﹣2),
对于y=﹣x+4,则y=0得x=,
∴C(,0),
∴S△AQC=AC×QF=×(+3)×=,S△OCR=OC?GR=××2=,S△AOP=OA?PE=×3×1=,
∴S△PQR=S△AQC+S△OCR﹣S△AOP=+﹣=.
7.(2015秋?建湖县期末)如图,直线l1:y1=kx+2(k≠0)与直线l2:y2=4x﹣4交于点P(m,4),直线l1分别交x轴、y轴于点A、B,直线l2交x轴于点C.
(1)求k、m的值;
(2)写出使得不等式kx+2<4x﹣4成立的x的取值范围;
(3)在直线l2上找点Q,使得S△QAC=S△BPC,求点Q的坐标.
【解答】解:(1)把P(m,4)代入y2=4x﹣4得4m﹣4=4,解得m=2,
所以P点坐标为(2,4),
把P(2,4)代入y1=kx+2得2k+2=4,解得k=1;
(2)当x>2时,kx+2<4x﹣4;
(3)当y=0时,x+2=0,解得x=﹣2,则A(﹣2,0);当x=0时,y1=x+2=2,则B(0,2),
当y=0时,4x﹣4=0,解得x=1,则C(1,0),
所以S△BPC=S△PAC﹣S△BAC=×(1+2)×4﹣×(1+2)×2=3,
设Q点坐标为(t,4t﹣4),
因为S△QAC=S△BPC=3,
所以×(1+2)×|4t﹣4|=3,解得t=或t=,
所以Q点的坐标为(,2)或(,2).
8.(2015秋?重庆校级期中)如图,在平面直角坐标系中,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B的坐标为(18,6).在x轴上有一点P(a,0),过点P作x轴的垂线分别交直线l1、l2于点C、D,直线l2与x轴交于点E.
(1)求直线l1、l2的表达式;
(2)若线段CD长为15,求此时a的值;
(3)若S△OBD=,求此时点P的坐标.
【解答】解:(1)设直线l1的表达式为y=k1x,
∵过点B(18,6),
∴18k1=6,
解得:k1=,
∴直线l1的表达式为y=x;
设直线l2的表达式为y=k2x+b,
∵过点A (0,24),B(18,6)
∴,解得:k2=﹣1,b=24,
∴直线l2的表达式y=﹣x+24;
(2)∵在x轴上有一点P(a,0),过点P作x轴的垂线分别交直线l1、l2于点C、D,
∴点C坐标为(a,a),点D坐标为(a,﹣a+24),
∴a﹣(﹣a+24)=15或﹣a+24﹣a=15,
解得:a=或a=;
(3)设点P(a,0),
由题意:××24×18=×24×18﹣×24×a,或××24×18=×24×a﹣×24×18,
解得a=1.8 或a=﹣(舍弃)
所以P点坐标为(﹣1.8,0).
题型8、与一次函数有关的几何动点问题
1.(2012?金东区一模)已知:如图,直线y=kx+b与x轴交于点A(8,0),与y轴交于点B(0,16),与直线y=x相交于点C.P(0,t)是y轴上的一个动点,过点P作直线l垂直y轴,与直线y=x相交于点D,与直线y=kx+b相交于点E,在直线l下方作一个等腰直角三角形DEF,使DF=DE,∠EDF=90°.
(1)求直线AB的解析式和C点的坐标;
(2)当点F落在x轴上时,求t的值;
(3)当t为何值时,以A,E,P,F为顶点的四边形是梯形?
【解答】解:(1)∵直线y=kx+b与x轴交于点A(8,0),与y轴交于点B(0,16),
∴,
解得,
所以,直线AB的解析式为y=﹣2x+16,
联立,
解得,
所以,C点坐标为(,);
(2)根据题意,点D、E的纵坐标都是t,
所以,﹣2x+16=t,
解得x=,
所以,点D(t,t),E(,t),
DE=|﹣t|,
∵点F在x轴上,
∴|﹣t|=t,
即﹣t=t或﹣t=﹣t,
解得t=或t=16,
所以,t的值为,16;
(3)①PE∥AF时,点F在x轴上,根据(2)的结论,
t=或16,
当t=16时,P、B、E三点重合,以A,E,P,F为顶点的是三角形,不符合题意舍去,
所以,t=;
②PF∥AE时,点D在点E的左边,
∵D(t,t),E(,t),
∴DE=﹣t=,
点F的纵坐标为:t﹣=,
∴点F(t,),
设直线PF的解析式为y=ex+f,
则,
解得,
所以,直线PF的解析式为y=x+t,
∵PF∥AE,
∴=﹣2,
解得t=;
③AP∥EF时,(i)若点P在y轴正半轴,则DE=t﹣=,
点F的纵坐标为t﹣=,
∴点F的坐标为(t,),
设直线EF的解析式为y=cx+d,则,
解得,
∴直线EF的解析式为y=﹣x+,
又∵A(8,0),P(0,t),
∴直线AP的解析式为y=﹣+t,
∵AP∥EF,
∴﹣=﹣1,
解得t=8,
(ii)若点P在y轴负半轴,则DE=﹣t=,
点F的纵坐标为t﹣=,
∴点F的坐标为(t,),
设直线EF的解析式为y=mx+n,则,
解得,
∴直线EF的解析式为y=x+,
又∵A(8,0),P(0,t),
∴直线AP的解析式为y=﹣+t,
∵AP∥EF,
∴﹣=1,
解得t=﹣8,
综上所述,t的值为,,8,﹣8.
2.(2016春?惠安县期末)如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x﹣2与x轴、y轴分别交于点E、F.
(1)求:①点D的坐标;
②经过点D,且与直线FC平行的直线的函数表达式;
(2)直线y=x﹣2上是否存在点P,使得△PDC为等腰直角三角形?若存在,求出点P 的坐标;若不存在,请说明理由.
(3)在平面直角坐标系内确定点M,使得以点M、D、C、E为顶点的四边形是平行四边形,请直接写出点M的坐标.
【解答】解:(1)①设点C的坐标为(m,2),
∵点C在直线y=x﹣2上,
∴2=m﹣2,
∴m=4,
即点C的坐标为(4,2),
∵四边形ABCD是矩形,
∴AB=CD=3,AD=BC=2,
∴点D的坐标为(1,2);
②设经过点D且与FC平行的直线函数表达式为y=x+b,
将D(1,2)代入y=x+b,得b=1,
∴经过点D且与FC平行的直线函数表达式为y=x+1;
(2)存在.
∵△EBC为等腰直角三角形,
∴∠CEB=∠ECB=45°,
又∵DC∥AB,
∴∠DCE=∠CEB=45°,
∴△PDC只能是以P、D为直角顶点的等腰直角三角形,
如图,①当∠D=90°时,延长DA与直线y=x﹣2交于点P1,
∵点D的坐标为(1,2),
∴点P1的横坐标为1,
把x=1代入y=x﹣2得,y=﹣1,
∴点P1(1,﹣1);
②当∠DPC=90°时,作DC的垂直平分线与直线y=x﹣2的交点即为点P2,
所以,点P2的横坐标为=,
把x=代入y=x﹣2得,y=,
所以,点P2(,),
综上所述,符合条件的点P的坐标为(1,﹣1)或(,);
(3)当y=0时,x﹣2=0,
解得x=2,
∴OE=2,
∵以点M、D、C、E为顶点的四边形是平行四边形,
∴若DE是对角线,则EM=CD=3,
∴OM=EM﹣OE=3﹣2=1,
此时,点M的坐标为(﹣1,0),
若CE是对角线,则EM=CD=3,
OM=OE+EM=2+3=5,
此时,点M的坐标为(5,0),
若CD是对角线,则平行四边形的中心坐标为(,2),
设点M的坐标为(x,y),
则=,=2,
解得x=3,y=4,
此时,点M的坐标为(3,4),
综上所述,点M的坐标为(﹣1,0),(5,0)(3,4).
3.(2015?泰州)已知一次函数y=2x﹣4的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为d1、d2.
(1)当P为线段AB的中点时,求d1+d2的值;
(2)直接写出d1+d2的范围,并求当d1+d2=3时点P的坐标;
(3)若在线段AB上存在无数个P点,使d1+ad2=4(a为常数),求a的值.
【解答】解:(1)对于一次函数y=2x﹣4,
令x=0,得到y=﹣4;令y=0,得到x=2,
∴A(2,0),B(0,﹣4),
∵P为AB的中点,
∴P(1,﹣2),
则d1+d2=3;
(2)①d1+d2≥2;
②设P(m,2m﹣4),
∴d1+d2=|m|+|2m﹣4|,
当0≤m≤2时,d1+d2=m+4﹣2m=4﹣m=3,
解得:m=1,此时P1(1,﹣2);
当m>2时,d1+d2=m+2m﹣4=3,
解得:m=,此时P2(,);
当m<0时,不存在,
综上,P的坐标为(1,﹣2)或(,);
(3)设P(m,2m﹣4),
∴d1=|2m﹣4|,d2=|m|,
∵P在线段AB上,
∴0≤m≤2,
∴d1=4﹣2m,d2=m,
∵d1+ad2=4,
∴4﹣2m+am=4,即(a﹣2)m=0,
∵有无数个点,
∴a=2.
4.(2015?温州模拟)如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0)、(12,6),直线y=﹣x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
(1)若直线y=﹣x+b平分矩形OABC的面积,求b的值;
(2)在(1)的条件下,当直线y=﹣x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
(3)在(1)的条件下,将矩形OABC沿DE折叠,若点O落在边BC上,求出该点坐标;若不在边BC上,求将(1)中的直线沿y轴怎样平移,使矩形OABC沿平移后的直线折叠,点O恰好落在边BC上.
【解答】解:(1)∵直线y=﹣x+b平分矩形OABC的面积,
∴其必过矩形的中心
由题意得矩形的中心坐标为(6,3),
∴3=﹣×6+b
解得b=12;
(2)如图1假设存在ON平分∠CNM的情况
①当直线PM与边BC和边OA相交时,过O作OH⊥PM于H
∵ON平分∠CNM,OC⊥BC,
∴OH=OC=6
由(1)知OP=12,
∴∠OPM=30°
∴OM=OP?tan30°=
当y=0时,由﹣x+12=0解得x=8,
∴OD=8
∴DM=8﹣;
②当直线PM与直线BC和x轴相交时
同上可得DM=8+(或由OM=MN解得);
(3)如图2假设沿DE将矩形OABC折叠,点O落在边BC上O′处连接PO′、OO′,则有PO′=OP
由(1)得BC垂直平分OP,∴PO′=OO′
∴△OPO′为等边三角形,∴∠OPD=30°
而由(2)知∠OPD>30°
所以沿DE将矩形OABC折叠,点O不可能落在边BC上;
如图3设沿直线y=﹣x+a将矩形OABC折叠,点O恰好落在边BC上O′处
连接P′O′、OO′,则有P′O′=OP′=a
由题意得:CP′=a﹣6,∠OPD=∠CO′O
在Rt△OPD中,tan∠OPD=
在Rt△OAO′中,tan∠CO′O=
∴=,即=,CO′=9
在Rt△CP′O′中,由勾股定理得:(a﹣6)2+92=a2
解得a=,12﹣=
所以将直线y=﹣x+12沿y轴向下平移个单位得直线y=﹣x+,将矩形OABC沿直线y=﹣x+折叠,点O恰好落在边BC上.
5.(2015?上虞区一模)如图1,平面直角坐标系中,已知A(0,4),B(5,0),D(3,0),点P从点A出发,沿y轴负方向在y轴上以每秒1个单位长度的速度匀速运动,过点P作PE∥x轴交直线AD于点E.
(1)设点P的运动时间为t(s),DE的单位长度为y,求y关于t的函数关系式,并写出t的取值范围;
(2)当t为何值时,以EP为半径的⊙E恰好与x轴相切?并求此时⊙E的半径;
(3)在点P的运动过程中,当以D,E,P三点为顶点的三角形是等腰三角形时,求此时t的值;
(4)如图2,将△ABD沿直线AD翻折,得到△AB′D,连结B′O,如果∠AOE=∠BOB′,求t值.(直接写出答案,不要求解答过程).
【解答】解:(1)∵A(0,4),B(5,0),D(3,0),
∴OA=4,OD=3,
由勾股定理得:AD==5,
①当0≤t≤4时,
∵PE∥x轴,
∴=,
∴=,
∴AE=t,
∴DE=5﹣t,
即y=5﹣t(0≤t≤4);
②当t>4时,y=t﹣5(t>4);
综上所述,y关于t的函数关系式为y=5﹣t(0≤t≤4),或y=t﹣5(t>4);
(2)作EM⊥OD于M,如图1所示:
则EM=4﹣t,
∵PE∥OD,
∴,
即,
解得:PE=t,AE=t,
当以EP为半径的⊙E恰好与x轴相切时,PE=EM,分两种情况:
①当0<t<4时,t=4﹣t,
解得:t=,此时PE=;
②当t>4时,t=t﹣4,
解得:t=16,此时12;
综上所述,当t为或16时,以EP为半径的⊙E恰好与x轴相切,⊙E的半径为或12;
(3)当0≤t≤4时,由PE=DE,
∴t=5﹣t,
解得:t=;
当t>4时,分三种情况:如图2所示:
①当DP=DE=t﹣5时,
由勾股定理得:OP2+OD2=DP2,
即(t﹣4)2+32=(t﹣5)2,
解得:t=8;
②当PE=PD时,
由勾股定理得:(t﹣4)2+32=(t)2,
解得:t=,或t=4(舍去);
∴t=;
③当PE=DE时,t=t﹣5
解得:t=10;
综上所述:当以D,E,P三点为顶点的三角形是等腰三角形时,t的值为或8或或10;
(4)设AD交BB′于F,连接BB′,如图3所示:
则AF⊥BB′,
∴∠AOD=∠BFD=90°,
又∵∠ADO=∠FDB,
∴∠OAD=∠FBD,△AOD∽△BFD,
∴,即,
∴BF=,
∴BB′=2BF=,
∵∠AOE=∠BOB′,∠OAD=∠FBD,
∴△AOE∽△BOB′,
∴,即,
∴AE==t,
∴t=.
6.(2015秋?宜兴市期末)如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=x相交于点A.
(1)求A点坐标;
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,则P点坐标是 (0,) ;
(3)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
【解答】解:(1)解方程组:得:
∴A点坐标是(2,3);
(2)设P点坐标是(0,y),
∵△OAP是以OA为底边的等腰三角形,
∴OP=PA,
∴22+(3﹣y)2=y2,
解得y=,
∴P点坐标是(0,),
故答案为(0,);
(3)存在;
由直线y=﹣2x+7可知B(0,7),C(,0),
∵S△AOC=××3=<6,S△AOB=×7×2=7>6,
∴Q点有两个位置:Q在线段AB上和AC的延长线上,设点Q的坐标是(x,y),
当Q点在线段AB上:作QD⊥y轴于点D,如图①,则QD=x,
∴S△OBQ=S△OAB﹣S△OAQ=7﹣6=1,
∴OB?QD=1,即×7x=1,
∴x=,
把x=代入y=﹣2x+7,得y=,
∴Q的坐标是(,),
当Q点在AC的延长线上时,作QD⊥x轴于点D,如图②则QD=﹣y,
∴S△OCQ=S△OAQ﹣S△OAC=6﹣=,
∴OC?QD=,即××(﹣y)=,
∴y=﹣,
把y=﹣代入y=﹣2x+7,解得x=,
∴Q的坐标是(,﹣),
综上所述:点Q是坐标是(,)或(,﹣).
7.(2014?新疆)如图,直线y=﹣x+8与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s)(0<t≤3).
(1)写出A,B两点的坐标;
(2)设△AQP的面积为S,试求出S与t之间的函数关系式;并求出当t为何值时,△AQP的面积最大?
(3)当t为何值时,以点A,P,Q为顶点的三角形与△ABO相似,并直接写出此时点Q的坐标.
【解答】解:(1)令y=0,则﹣x+8=0,
解得x=6,
x=0时,y=y=8,
∴OA=6,OB=8,
∴点A(6,0),B(0,8);
(2)在Rt△AOB中,由勾股定理得,AB===10,
∵点P的速度是每秒2个单位,点Q的速度是每秒1个单位,
∴AP=2t,
AQ=AB﹣BQ=10﹣t,
∴点Q到AP的距离为AQ?sin∠OAB=(10﹣t)×=(10﹣t),
∴△AQP的面积S=×2t×(10﹣t)=﹣(t2﹣10t)=﹣(t﹣5)2+20,
∵﹣<0,0<t≤3,
∴当t=3时,△AQP的面积最大,S最大=﹣(3﹣5)2+20=;
(3)若∠APQ=90°,则cos∠OAB=,
∴=,
解得t=,
若∠AQP=90°,则cos∠OAB=,
∴=,
解得t=,
∵0<t≤3,
∴t的值为,
此时,OP=6﹣2×=,
PQ=AP?tan∠OAB=(2×)×=,
∴点Q的坐标为(,),
综上所述,t=秒时,以点A,P,Q为顶点的三角形与△ABO相似,此时点Q的坐标为(,).
8.(2014?新余模拟)如图,在平面直角坐标系中,直线AB分别与x轴、y轴相交于A,B两点,OA、OB的长分别是方程x2﹣14x+48=0的两根,且OA<OB.
(1)求点A,B的坐标.
(2)过点A作直线AC交y轴于点C,∠1是直线AC与x轴相交所成的锐角,sin∠1=,求直线AC的解析式.
(3)若点M(m,m﹣5)在△AOC的内部,求m的取值范围.
【解答】解:(1)因式分解得,(x﹣6)(x﹣8)=0,
所以,x﹣6=0,x﹣8=0,
解得x1=6,x2=8,
∵OA<OB,
∴OA=6,OB=8,
∴点A(6,0),B(0,8);
(2)∵sin∠1=,∠1=∠COA,
∴设OC=3k,AC=5k,
由勾股定理得,OC2+OA2=AC2,
即(3k)2+62=(5k)2,
解得k=,
∴OC=3k=3×=,
∴点C(0,﹣),
设直线AC的解析式为y=kx+b,
则,
解得,
所以,直线AC的解析式为y=x﹣;
(3)∵点M(m,m﹣5)在△AOC的内部,
∴,
解不等式①得,m<5,
解不等式②得,m>2,
∴m的取值范围2<m<5.
9.(2013?维扬区校级二模)如图,已知直线y=x+4与x轴、y轴分别相交于点A、B,点C从O点出发沿射线OA以每秒1个单位长度的速度匀速运动,同时点D从A点出发沿AB以每秒1个单位长度的速度向B点匀速运动,当点D到达B点时C、D都停止运动.点E是CD的中点,直线EF⊥CD交y轴于点F,点E′与E点关于y轴对称.点C、D的运动时间为t(秒).
(1)当t=1时,AC= 2 ,点D的坐标为 (,) ;
(2)设四边形BDCO的面积为S,当0<t<3时,求S与t的函数关系式;
(3)当直线EF与△AOB的一边垂直时,求t的值;
(4)当△EFE′为等腰直角三角形时,直接写出t的值.
【解答】解:(1)如图1,过D作DH⊥AC于H,
∵直线y=x+4与x轴、y轴分别相交于点A,A、B,
∴A(﹣3,0),B(0,4),
∴AO=3,BO=4,
∴AB===5,
当0≤t≤3时,如图1,
∵CO=t,AD=t,
∴AC=3﹣t,DH=AD?sin∠BAO=t,AH=ADcos∠BAO=t,
当t=1时,AC=3﹣1=2,
点D的坐标为(,);
(2)∵AO=3,BO=4,AB=5
∴sin∠BAO==,cos∠BAO==
过D作DH⊥AC于H,
当0≤t≤3时,如图1,
∵CO=t,AD=t,
∴AC=3﹣t,DH=AD?sin∠BAO=t,
∴S=S△ABO﹣S△ADC=×3×4﹣?(3﹣t)?t,
S=t2﹣t+6(0<t<3).
(3)如图2,当EF⊥BO时,
∵EF⊥CD,
∴CD∥BO,
∴∠ACD=90°,
在Rt△ADC中,=cos∠BAO,
∴=,
t=,
当EF⊥AB时,如图3,
∵EF⊥CD,
∴直线CD和直线AB重合,
∴C点和A点重合,
∴t=3.
(4)①如图4,
当0<t<,且且重叠部分为等腰梯形PEQM时,
则∠PEQ=∠MQE,
∵菱形CDMN,
∴CD∥MN,
∴∠MQE=∠CEQ,
∵EF⊥CD,
即∠CEF=90°,
∴∠CEQ=45°,
∴∠ACD=∠CEQ=45°,
过D作DH⊥AC于H,则△DHC是等腰直角三角形,
∴DH=HC,
∴t=3﹣t﹣t,
∴t=;
②如图5,
当<t<5,且重叠部分为等腰梯形EHNK时,
同理可得∠CHE=45°,
连接DHDH,
∵EF垂直平分CD,
∴CH=DH,∠DHE=∠CHE=45°,
∴∠DHC=90°,
∴DH=t,
而CH=CO﹣HO=CO﹣(AO﹣AH)=t﹣(3﹣t),
∴t﹣(3﹣t)=t,
∴t=.
10.(2013?莆田模拟)阅读下面材料,并解决问题:
(I)如图4,等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5.则∠APB= 150° ,由于PA,PB不在一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌ △ABP .这样,就可以利用全等三角形知识,将三条线段的长度转化到一个三角形中从而求出∠APB的度数.
(II)(拓展运用)已知△ABC三边长a,b,c满足.
(1)试判断△ABC的形状 等腰直角三角形
(2)如图1,以点A为原点,AB所在直线为x轴建立平面直角坐标系,直接出点B,C的坐标 B(12,0),C(6,6) ;
(3)如图2,过点C作∠MCN=45°交AB于点M,N.请证明AM2+BN2=MN2;
(4)在(3)的条件下,若点N的坐标是(8,0),则点M的坐标为 (3,0) ;此时MN= 5 .并求直线CM的解析式.
(5)如图3,当点M,N分布在点B异侧时.则(3)中的结论还成立吗?
【解答】解:(Ⅰ)∵△ABC是等边三角形,
∴∠BAC=60°,
∵△ABP绕顶点A旋转到△ACP′处,
∴△ACP′≌△ABP,
∴P′A=PA=3,PB=P′C=4,∠PAP′=∠BAC=60°,
∴△APP′是等边三角形,
∴∠AP′P=60°,PP′=PA=3,
在△P′PC中,P′P2+P′C2=32+42=25=PC2,
∴∠PP′C=90°,
∴∠APB=∠AP′C=∠AP′P+∠PP′C=60°+90°=150°,
∴∠APB=150°;
故答案是:150°,△ABP;
(Ⅱ)(1)整理得,|a﹣6|+(c﹣12)2+=0,
由非负数的性质得,a﹣6=0,c﹣12=0,b﹣6=0,
解得a=b=6,c=12,
∵a2+b2=(6)2+(6)2=144=c2,
∴△ABC是直角三角形,
又∵a=b,
∴△ABC是等腰直角三角形;
(2)∵AB=c=12,
∴点B(12,0),
过点C作CD⊥x轴于D,则AD=CD=AB=×12=6,
∴点C的坐标为(6,6);
(3)如图,把△ACM绕点C逆时针旋转90°得到△BCM′,连接M′N,
由旋转的性质得,AM=BM′、CM=CM′、∠CAM=∠CBM′=45°,∠ACM=∠BCM′,
∴∠M′BN=∠ABC+∠CBN′=45°+45°=90°,
∵∠MCN=45°,
∴∠M′CN=∠BCN+∠BCM′=∠BCN+∠ACM=90°﹣∠MCN=90°﹣45°=45°,
∴∠MCN=∠M′CN,
在△MCN和△M′CN中,
,
∴△MCN≌△M′CN(SAS),
∴MN=M′N,
在Rt△M′NB中,BM′2+BN2=M′N2,
∴AM2+BN2=MN2;
(4)设AM=x,
∵点N的坐标是(8,0),
∴AN=8,BN=12﹣8=4,
∴MN=8﹣x,
由(3)的结论,x2+42=(8﹣x)2,
解得x=3,
∴AM=3,MN=8﹣3=5,
∴点M的坐标(3,0);
设直线CM的解析式为y=kx+b,
∵点C(6,6),M(3,0),
∴,
解得,
∴设直线CM的解析式为y=2x﹣6;
(5)如图,∵△ABC是等腰直角三角形,
∴∠CAB=∠CBA=45°,
把△BCN绕点C顺时针旋转90°得到△ACN′,
由旋转的性质得,AN′=BN,CN′=CN,∠CAN′=∠CBN=135°,
∴∠MAN′=135°﹣45°=90°,
∴点N′在y轴上,
∵∠MCN=45°,
∴∠MCN′=90°﹣45°=45°,
∴∠MCN=∠MCN′,
在△MCN和△MCN′中,
,
∴△MCN≌△MCN′(SAS),
∴MN=MN′,
在Rt△AMN′中,AM2+AN′2=MN′2,
∴AM2+BN2=MN2.
故答案为:(Ⅰ)150°,△ABP;(1)等腰直角三角形;(2)B(12,0),C(6,6);(4)(3,0),5.
11.(2013秋?镇江月考)如图,直线l1的解析表达式为:y=3x﹣3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
(1)求△ADC的面积;
(2)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,则点P的坐标为 (6,﹣3) ;
(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、D、C、H为顶点的四边形是平行四边形?若存在,请直接写出点H的坐标;若不存在,请说明理由.
【解答】解:(1)令y=0,则3x﹣3=0,
解得x=1,
∴点D(1,0),
∴AD=4﹣1=3,
设直线l2的解析式为y=kx+b(k≠0),
则,
解得,
∴设直线l2的解析式为y=﹣x+6,
联立,
解得,
∴点C的坐标为(2,3),
∴△ADC的面积=×3×3=;
(2)∵△ADP与△ADC的面积相等,点P是异于点C的点,
∴点P的纵坐标为﹣3,
∴﹣x+6=﹣3,
解得x=6,
∴点P(6,﹣3);
故答案为:(6,﹣3);
(3)①AC是平行四边形的对角线时,CH=AD=3,
点H的横坐标为2+3=5,
所以,点H的坐标为(5,3),
②CD是平行四边形的对角线时,CH=AD=3,
点H的横坐标是2﹣3=﹣1,
所以,点H的坐标为(﹣1,3),
③AD是对角线时,AD=,
所以,AD的中点坐标为(,0),
∵平行四边形的对角线互相平分,
∴设点H(x,y),则=,=0,
解得x=3,y=﹣3,
∴点H的坐标为(3,﹣3),
综上所述,存在点H(5,3)或(﹣1,3)或(3,﹣3),使以A、D、C、H为顶点的四边形是平行四边形.
12.(2009?随州)如图1,在Rt△A′OB′中,∠B′A′0=90°,A′,B′两点的坐标分别为(2,﹣1)和(0,﹣5),将A′0B′绕点O逆时针方向旋转90°,使OB’落在x轴正半轴上,得△AOB,点A′的对应点是A,点B’的对应点是B.
(1)写出A,B两点的坐标,并求直线AB的解析式;
(2)如图2,将△A0B沿垂直于x轴的线段CD折叠,(点C在x轴上,且不与点B重合,点D在线段AB上),使点B落在x轴上,对应点为点E,设点C的坐标为(x,0).
①当x为何值时,线段DE平分△AOB的面积;
②是否存在这样的点使得△AED为直角三角形?若存在,求出点C的坐标;若不存在,请说明理由.
③设△CDE与△AOB重叠部分的面积为S,直接写出S与点C的横坐标x之间的函数关系式(包括自变量x的取值范围).
【解答】解:(1)A(1,2),B(5,0),
设直线AB的解析式为y=kx+b,则有:
,
解得:,
∴直线AB的解析式为y=﹣x+.
(2)①当x=时,CD=y==,S△DEB=×5×=>3,
∴点E在O的右边.
由题意,得:S△DEB=×2(5﹣x)×=,x=5+(舍去),
∴x=5﹣.
②当∠ADE=90°时,得∠DBE=∠DEB=45°,舍去,
当∠EAD=90°时,点E与点O重合,得x=.
当∠AED=90°时,作AH⊥OB于H,证明△AHE∽△ECD,可得HE=1.
∴OE=2.
∴2+2(5﹣x)
一、基础知识及考点剖析
考点1、常量和变量
1.(2016春?迁安市期中)如果用总长为120m的篱笆围成一个长方形场地,设长方形的面积为S(m2),周长为C(m),一边长为a(m),那么S,C,a中是变量的是( )21世纪教育网版权所有
A.S和C B.S和a C.C和a D.S,C,a
【解答】解:S(m2),周长为C(m),一边长为a(m),那么S,a是变量,
故选:B.
2.(2015秋?上城区期末)在圆周长计算公式C=2πr中,对半径不同的圆,变量有( )
A.C,r B.C,π,r C.C,πr D.C,2π,r
【解答】解:在圆周长计算公式C=2πr中,对半径不同的圆,变量有:C,r.
故选:A.
3.(2014春?上街区校级期中)某公司销售部门发现,该公司的销售收入随销售量的变化而变化,其中 销售量 是自变量, 销售收入 是因变量.21教育网
【解答】解:根据题意知,公司的销售收入随销售量的变化而变化,
所以销售量是自变量,收入数为因变量.
故答案为:销售量,销售收入.
4.下表是小华做观察水的沸腾实验时所记录的数据:
(1)时间是8分钟时,水的温度为 100℃ ;
(2)此表反映了变量 温度 和 时间 之间的关系,其中 时间 是自变量, 温度 是因变量;
(3)在 0至8分钟 时间内,温度随时间增加而增加; 8至12分钟 时间内,水的温度不再变化.
【解答】解:(1)第8分钟时水的温度为100℃;
(2)反映的温度随着时间的变化而变化的,时间是自变量,温度是因变量;
(3)观察表格发现在0至8分钟时间内,温度随时间增加而增加;8至12分钟时间内,水的温度不再变化.
故答案为:(1)100℃(2)温度,时间,时间,温度;(3)0至8分钟,8至12分钟.
5.(2014春?通川区校级期中)已知某易拉罐厂设计一种易拉罐,在设计过程中发现符合要求的易拉罐的底面半径与铝用量有如下关系:21cnjy.com
底面半径x(cm)
1.6
2.0
2.4
2.8
3.2
3.6
4.0
用铝量y(cm3)
6.9
6.0
5.6
5.5
5.7
6.0
6.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当易拉罐底面半径为2.4cm时,易拉罐需要的用铝量是多少?
(3)根据表格中的数据,你认为易拉罐的底面半径为多少时比较适宜?说说你的理由.
(4)粗略说一说易拉罐底面半径对所需铝质量的影响.
【解答】解:(1)易拉罐底面半径和用铝量的关系,易拉罐底面半径为自变量,用铝量为因变量;
(2)当底面半径为2.4cm时,易拉罐的用铝量为5.6cm3
(3)易拉罐底面半径为2.8cm时比较合适,因为此时用铝较少,成本低
(4)当易拉罐底面半径在1.6~2.8cm变化时,用铝量随半径的增大而减小,当易拉罐底面半径在2.8~4.0cm间变化时,用铝量随半径的增大而增大.21·cn·jy·com
考点2、函数及其表示方式
1.(2014秋?太原期中)下列图象不能表示变量y是变量x的函数的是( )
A. B. C. D.
【解答】解:A、对于x的每一个取值,y都有唯一确定的值,故A正确;
B、对于x的每一个取值,y有不唯一确定的值,故B错误;
C、对于x的每一个取值,y都有唯一确定的值,故C正确;
D、对于x的每一个取值,y都有唯一确定的值,故D正确;
故选:B.
2.(2015秋?青岛校级期末)下列变量之间的关系:
(1)凸多边形的对角线条数与边数;
(2)三角形面积与它的底边(高为定值);
(3)x﹣y=3中的x与y;
(4)圆的面积与圆的半径;
(5)y=|x|中的x与y.
其中成函数关系的有( )
A.2个 B.3个 C.4个 D.5个
【解答】解:(1)凸多边形的对角线条数与边数是函数关系;
(2)三角形面积与它的底边(高为定值)是函数关系;
(3)x﹣y=3中的x与y是函数关系;
(4)圆的面积与圆的半径是函数关系;
(5)y=|x|中的x与y是函数关系;
故选:D..
3.(2013?北京)如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2.设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. B. C. D.
【解答】解:作OC⊥AP,如图,则AC=AP=x,
在Rt△AOC中,OA=1,OC===,
所以y=OC?AP=x?(0≤x≤2),
所以y与x的函数关系的图象为A选项.
故选:A.
排除法:
很显然,并非二次函数,排除B选项;
采用特殊位置法;
当P点与A点重合时,此时AP=x=0,S△PAO=0;
当P点与B点重合时,此时AP=x=2,S△PAO=0;
当AP=x=1时,此时△APO为等边三角形,S△PAO=;
排除B、C、D选项,
故选:A.
4.(2013?黄石)如图,已知某容器都是由上下两个相同的圆锥和中间一个与圆锥同底等高的圆柱组合而成,若往此容器中注水,设注入水的体积为y,高度为x,则y关于x的函数图象大致是( )
A. B. C. D.
【解答】解:如图,①水在下边的圆锥体内时,水面的半径为xtanα,
水的体积y=π(xtanα)2?x=πtan2α?x3,
所以,y与x成立方关系变化,即小于直线增长;
②水面在圆柱体内时,y是x的一次函数;
③水在上边的圆锥体时,水的高度增长的速度与①中相反,即直线变缓了,
纵观各选项,只有A选项符合.
故选A.
5.(2015?广元)如图,矩形ABCD中,AB=3,BC=4,点P从A点出发,按A→B→C的方向在AB和BC上移动.记PA=x,点D到直线PA的距离为y,则y关于x的函数大致图象是( )
A. B. C. D.
【解答】解:(1)当点P在AB上移动时,
点D到直线PA的距离为:
y=DA=BC=4(0≤x≤3).
(2)如图1,当点P在BC上移动时,,
∵AB=3,BC=4,
∴AC=,
∵∠PAB+∠DAE=90°,∠ADE+∠DAE=90°,
∴∠PAB=∠DAE,
在△PAB和△ADE中,
∴△PAB∽△ADE,
∴,
∴,
∴y=(3<x≤5).
综上,可得
y关于x的函数大致图象是:
.
故选:D.
6.(2015?烟台)如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
A. B. C. D.
【解答】解:如图1,CH是AB边上的高,与AB相交于点H,,
∵∠C=90°,∠BAC=30°,AB=8,
∴AC=AB×cos30°=8×=4,BC=AB×sin30°=8×=4,
∴CH=AC×,AH=,
(1)当0≤t≤2时,
S==t2;
(2)当2时,
S=﹣
=t2[t2﹣4t+12]
=2t﹣2
(3)当6<t≤8时,
S=[(t﹣2)?tan30°]×[6﹣(t﹣2)]×[(8﹣t)?tan60°]×(t﹣6)
=[]×[﹣t+2+6]×[﹣t]×(t﹣6)
=﹣t2+2t+4﹣t2﹣30
=﹣t2﹣26
综上,可得
S=
∴正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是A图象.
故选:A.
7.(2015?本溪)如图,在△ABC中,∠C=90°,点P是斜边AB的中点,点M从点C向点A匀速运动,点N从点B向点C匀速运动,已知两点同时出发,同时到达终点,连接PM、PN、MN,在整个运动过程中,△PMN的面积S与运动时间t的函数关系图象大致是( )
A. B. C. D.
【解答】解:如图1,连接CP,
,
∵点P是斜边AB的中点,
∴S△ACP=S△BCP=S△ABC,
出发时,S△PMN=S△BCP=S△ABC;
∵两点同时出发,同时到达终点,
∴点N到达BC的中点时,点M也到达AC的中点,
∴S△PMN=S△ABC;
结束时,S△PMN=S△ACP=S△ABC,
在整个运动过程中设BC=a,AC=b,
∴S=[ab﹣VN?t?﹣(a﹣VN?t)?VM?t﹣(b﹣VM?t)?]
=(ab﹣VNb?t﹣aVM?t+VNVM?t2﹣ab+aVM?t)
=VNVM?t2﹣(VNb+aVM)t+ab,
∴△MPN的面积大小变化情况是:先减小后增大,而且是以抛物线的方式变化,
∴△PMN的面积S与运动时间t的函数关系图象大致是:
.
故选:A.
8.(2014?徐州)如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为 y=﹣3x+18 .
【解答】解:∵点P沿边DA从点D开始向点A以1cm/s的速度移动;点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.
∴当Q到达B点,P在AD的中点时,△PAQ的面积最大是9cm2,设正方形的边长为acm,
∴×a×a=9,
解得a=6,即正方形的边长为6,
当Q点在BC上时,AP=6﹣x,△APQ的高为AB,
∴y=(6﹣x)×6,即y=﹣3x+18.
故答案为:y=﹣3x+18.
9.(2013?咸宁)“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 ①③④ .(把你认为正确说法的序号都填上)
【解答】解:根据图象可知:
龟兔再次赛跑的路程为1000米,故①正确;
兔子在乌龟跑了40分钟之后开始跑,故②错误;
乌龟在30﹣﹣40分钟时的路程为0,故这10分钟乌龟没有跑在休息,故③正确;
y1=20x﹣200(40≤x≤60),y2=100x﹣4000(40≤x≤50),当y1=y2时,兔子追上乌龟,
此时20x﹣200=100x﹣4000,
解得:x=47.5,
y1=y2=750米,即兔子在途中750米处追上乌龟,故④正确.
综上可得①③④正确.
故答案为:①③④.
10.(1999?哈尔滨)函数y=中,自变量x的取值范围是 x≥,且x≠2 .
【解答】解:2x﹣1≥0,x﹣2≠0,解得:x≥,且x≠2.
考点3、一次函数的概念
1.(2016春?潮南区期末)已知y=(m+1),如果y是x的正比例函数,则m的值为( )
A.1 B.﹣1 C.1,﹣1 D.0
【解答】解:由y=(m+1),如果y是x的正比例函数,得
,
解得m=1,
故选:A.
2.(2015秋?陕西校级期末)若y=(m﹣1)是正比例函数,则m的值为( )
A.1 B.﹣1 C.1或﹣1 D.或﹣
【解答】解:根据正比例函数的定义,可得2﹣m2=1,m﹣1≠0,∴m=﹣1.
故选B.
3.(2012?江西模拟)当m= 1或﹣5或 时,函数y=(m+5)x2m﹣1+7x﹣3(x≠0)是一个一次函数.
【解答】解:①,
解得:m=1
根据题意得:2m﹣1=1,
解得:m=1,
此时函数化简为y=13x﹣3.
②2m﹣1=0,
解得:m=,
此时函数化简为y=7x+2.5;
③m+5=0,
解得:m=﹣5,
此时函数化简为y=7x﹣3.
故答案为:1或﹣5或.
4.(1999?贵阳)已知y=(k﹣3)k2x﹣2k﹣2是正比例函数,则k= ﹣1 .
【解答】解:根据定义﹣2k﹣2=0,(k﹣3)k2≠0,
解得:k=﹣1,满足(k﹣3)k2≠0,
所以k=﹣1.
故填﹣1.
5.(2015春?大名县期末)要使y=(m﹣2)x|m﹣1|+3是关于x的一次函数,则m= 0 .
【解答】解:根据一次函数的定义可得:m﹣2≠0,|m﹣1|=1,
由|m﹣1|=1,解得:m=0或2,
又m﹣2≠0,m≠2,
∴m=0.
故答案为:0.
6.(2015?石家庄模拟)新定义[a,b]为一次函数(其中a≠0,且a,b为实数)的“关联数”,若“关联数”[3,m+2]所对应的一次函数是正比例函数,则关于x的方程+=1的解为 .
【解答】解:根据“关联数”[3,m+2]所对应的一次函数是正比例函数,
得到y=3x+m+2为正比例函数,即m+2=0,
解得:m=﹣2,
则分式方程为﹣=1,
去分母得:2﹣(x﹣1)=2(x﹣1),
去括号得:2﹣x+1=2x﹣2,
解得:x=,
经检验x=是分式方程的解.
故答案为:x=.
考点4、一次函数的图象与性质
1.(2016?福州校级模拟)函数y=|2x|的图象是( )
A. B. C. D.
【解答】解:函数y=|2x|,当x≥0时,y=2x;当x≤0时,y=﹣2x,
故图象C符合,
故选C
2.(2015春?温岭市期末)定义运算*为:a*b=如:1*(﹣2)=﹣1×(﹣2)=2,则函数y=2*x的图象大致是( )
A. B. C. D.
【解答】解:y=2※x=,
x>0时,图象是y=2x的正比例函数中y轴右侧的部分;x≤0时,图象是y=﹣2x的正比例函数中y左侧的部分,
故选:C.
3.(1998?广东)已知y是x的函数,y与x﹣1成正比例,如果这个函数的图象经过点(a,a)(a≠0),那么它的图象大致是( )
A. B. C. D.
【解答】解:∵y与x﹣1成正比例,
∴y=k(x﹣1)(k≠0),
当x=1时,y=0,与k值无关,
∴直线y=k(x﹣1)经过定点(1,0),
∵点(a,a)(a≠0),
∴点(a,a)在第一三象限的平分线上,
∴直线的大致图象为B选项图象.
故选B.
4.(2015春?和平区期末)如图,两个不同的一次函数y=ax+b与y=bx+a的图象在同一平面直角坐标系的位置可能是( )
A. B. C. D.
【解答】解:A、若经过第一、二、三象限的直线为y=ax+b,则a>0,b>0,所以直线y=bx+a经过第一、二、三象限,所以A选项错误;
B、若经过第一、二、四象限的直线为y=ax+b,则a<0,b>0,所以直线y=bx+a经过第一、三、四象限,所以B选项错误;
C、若经过第一、三、四象限的直线为y=ax+b,则a>0,b<0,所以直线y=bx+a经过第一、二、四象限,所以C选项正确;
D、若经过第一、二、三象限的直线为y=ax+b,则a>0,b>0,所以直线y=bx+a经过第一、二、三象限,所以D选项错误;
故选C.
5.(2015秋?西安校级期末)直线y=kx+b经过一、三、四象限,则直线y=bx﹣k的图象只能是图中的( )
A. B. C. D.
【解答】解:∵直线y=kx+b经过第一、三、四象限,
∴k>0,b<0,
∴﹣k<0,
∴直线y=bx﹣k经过第二、三、四象限.
故选C.
6.(2013秋?南京期末)在同一平面直角坐标中,关于下列函数:①y=x+1;②y=2x+1;③y=2x﹣1;④y=﹣2x+1的图象,说法不正确的是( )
A.②和③的图象相互平行
B.②的图象可由③的图象平移得到
C.①和④的图象关于y轴对称
D.③和④的图象关于x轴对称
【解答】解:由题意得:y=2x+1与y=2x﹣1比例系数相等;y=2x﹣1与y=﹣2x+1的比例系数互为相反数,
所以②和③的图象相互平行,③和④的图象关于x轴对称,
故A、B、D正确,C错误,
故选C.
7.(2006?贵阳)函数y1=x+1与y2=ax+b的图象如图所示,这两个函数的交点在y轴上,那么y1、y2的值都大于零的x的取值范围是 ﹣1<x<2 .
【解答】解:根据图示及数据可知,
函数y1=x+1与x轴的交点坐标是(﹣1,0),
由图可知y2=ax+b与x轴的交点坐标是(2,0),
所以y1、y2的值都大于零的x的取值范围是:﹣1<x<2.
8.(2006?西岗区)如图是一次函数y1=ax+b,y2=kx+c的图象,观察图象,写出同时满足y1≥0,y2≥0时x的取值范围 ﹣2≤x≤1 .
【解答】解:根据图象和图中数据可知,同时满足y1≥0,y2≥0时,
x的取值范围﹣2≤x≤1.
9.(2012春?丘北县校级期中)如图,已知函数y=2x﹣5,观察图象回答下列问题:
(1)x <2.5 时,y<0;
(2)y <﹣5 时,x<0.
【解答】解:(1)∵当x<2.5时函数的图象在x轴的下方,
∴x<2.5时,y<0;
(2)∵当y<﹣5时函数图象在y轴的右侧,
∴y<﹣5时,x<0.
故答案为:<2.5,<﹣5.
10.作函数y=2x﹣4的图象,并根据图象回答下列问题.
(1)当﹣2≤x≤4,求函数y的取值范围.
(2)当x取何值时,y<0?y=0?y>0?
【解答】解:当x=0时,y=﹣4;
当y=0时,2x﹣4=0,
解得x=2,
∴函数图象与两坐标轴的交点为(0,﹣4)(2,0).
图象如下:
(1)x=﹣2时,y=2×(﹣2)﹣4=﹣8,
x=4时,y=2×4﹣4=4,
∵k=2>0,
∴y随x的增大而增大,
∴﹣8≤y≤4;
(2)x<2时,y<0;
x=2时,y=0;
x>2时,y>0.
考点5、一次函数的性质
1.(2015春?武平县校级月考)对于y=k2x(k≠0)的图象下列说法不正确的是( )
A.是一条直线 B.过点(,k)
C.经过一、三象限或二、四象限 D.y随x增大而增大
【解答】解:∵y=k2x(k≠0),
∴k2>0.
∴y=k2x(k≠0)的图象是正比例函数的图象,图象在第一、三象限,y随x的增大而增大,图象是一条直线.
当x=时,y=k2x=.
即y=k2x(k≠0)的图象过点().
由上可得,选项A的说法正确,选项B的说法正确,选项C的说法不正确,选项D的说法正确.
故选C.
2.(2011?黑龙江模拟)已知四条直线y=kx﹣3,y=﹣1,y=3和x=1所围成的四边形的面积是12,则k的值为( )
A.1或2 B.1或﹣2 C.﹣1或2 D.﹣1或﹣2
【解答】解:如图所示,根据题意,得
A(1,3),B(1,﹣1),C(,﹣1),D(,3).
显然ABCD是梯形,且梯形的高是4,根据梯形的面积是12,则梯形的上下底的和是6,则有
①当k<0时,1﹣+1﹣=6,
∴2﹣=6,
∴=﹣4,
解得k=﹣2;
②当k>0时,﹣1+﹣1=6,
∴=8,
解得k=1.
综上所述,则k=﹣2或1.
故选B.
3.(2016?江西校级模拟)设0<k<2,关于x的一次函数y=kx+2(1﹣x),当1≤x≤2时的最大值是( )
A.2k﹣2 B.k﹣1 C.k D.k+1
【解答】解:原式可以化为:y=(k﹣2)x+2,
∵0<k<2,
∴k﹣2<0,则函数值随x的增大而减小.
∴当x=1时,函数值最大,最大值是:(k﹣2)+2=k.
故选:C.
4.(2014?余姚市校级自主招生)对每个x,y是y1=2x,y2=x+2,y3=三个值中的最大值,则当x变化时,函数y的最小值为( )
A.4 B.6 C.8 D.
【解答】解:分别联立y1、y2,y1、y3,y2、y3,可知y1、y2的交点A(2,4);y1、y3的交点B(,);y2、y3的交点C(4,6),
∴当x≤2时,y最小=9;
当2<x≤时,y最小=;
当<x≤4时,y最小=;
当x>4时,y最小=8.
故选D.
5.(2012?上城区二模)已知四条直线y=kx﹣3,y=﹣1,y=3和x=1所围成的四边形的面积是8,则k的值为( )
A.或﹣4 B.或4 C.或﹣2 D.2或﹣2
【解答】解:∵y=﹣1,y=3,
∴围成的四边形是梯形,
直线y=﹣1,y=3之间的距离为3﹣(﹣1)=3=1=4,
所以,梯形的高为4,
联立,解得,
联立,解得,
①交点在直线x=1的左侧时,(1﹣+1﹣)×4=8,
解得k=﹣4,
②交点在直线x=1的右侧时,(﹣1+﹣1)×4=8,
解得k=,
综上,k的值为或﹣4.
故选A.
6.(2016春?泗县期中)要使直线y=(2m﹣3)x+(3n+1)的图象经过一、二、四象限,则m与n的取值为( )
A.m>,n>﹣ B.m>3,n>﹣3 C.m<,n<﹣ D.m<,n>﹣
【解答】解:∵直线y=(2m﹣3)x+(3n+1)的图象经过一、二、四象限,
∴,解得.
故选D.
7.(2014秋?郑州期末)下图中表示一次函数y=mx+n与正比例函数y=nx(m,n是常数,且mn<0)图象的是( )
A. B. C. D.
【解答】解:A、根据图中正比例函数y=nx的图象知,n<0;∵m,n是常数,且mn<0,∴m>0,∴一次函数y=mx+n的图象经过第一、三、四象限;故本选项错误;
B、根据图中正比例函数y=nx的图象知,n>0;∵m,n是常数,且mn<0,∴m<0,∴一次函数y=mx+n的图象经过第一、二、四象限;故本选项正确;
C、根据图中正比例函数y=nx的图象知,n<0;∵m,n是常数,且mn<0,∴m>0,∴一次函数y=mx+n的图象经过第一、三、四象限;故本选项错误;
D、根据图中正比例函数y=nx的图象知,n>0;∵m,n是常数,且mn<0,∴m<0,∴一次函数y=mx+n的图象经过第一、二、四象限;故本选项错误;
故选B.
8.(2015秋?丹阳市校级月考)已知一次函数y=kx﹣1的图象不经过第二象限,则正比例函数y=(k+1)x必定经过第 一、三 象限.
【解答】解:∵一次函数y=kx﹣1的图象经过第一、三、四象限
∴k>0
∴k+1>0
∴正比例函数y=(k+1)x必定经过第一、三象限.
9.(2012?北海)如图,点A的坐标为(﹣1,0),点B在直线y=2x﹣4上运动,当线段AB最短时,点B的坐标是 (,﹣) .
【解答】解:设AB′解析式为y=kx+b,
∵AB′⊥BB′,BB′解析式为y=2x﹣4,k1×k2=﹣1,
∴2k=﹣1,
k=﹣,于是函数解析式为y=﹣x+b,
将A(﹣1,0)代入y=﹣x+b得,+b=0,b=﹣,
则函数解析式为y=﹣x﹣,
将两函数解析式组成方程组得,
,
解得,故B点坐标为(,﹣).
故答案为(,﹣).
10.(2012?麻城市校级自主招生)设直线kx+(k+1)y﹣1=0与坐标轴所构成的直角三角形的面积为Sk,则S1+S2+…+S2008= .
【解答】解:∵kx+(k+1)y﹣1=0
∴当x=0时,y=;当y=0时,x=
∴Sk=××=,
根据公式可知,S1+S2+…+S2008=[﹣+﹣+…+﹣]=(1﹣)=.
11.(1998?大连)已知一次函数,若y随x的增大而减小,则m的值为 .
【解答】解:∵函数是一次函数,
∴
解得:m=﹣,
故答案为:.
12.(2014?自贡)一次函数y=kx+b,当1≤x≤4时,3≤y≤6,则的值是 2或﹣7 .
【解答】解:当k>0时,此函数是增函数,
∵当1≤x≤4时,3≤y≤6,
∴当x=1时,y=3;当x=4时,y=6,
∴,解得,
∴=2;
当k<0时,此函数是减函数,
∵当1≤x≤4时,3≤y≤6,
∴当x=1时,y=6;当x=4时,y=3,
∴,解得,
∴=﹣7.
故答案为:2或﹣7.
13.已知一次函数y=(m﹣1)+m的图象经过第二、三、四象限,则m的值是 ﹣ .
【解答】解:若一次函数y=(m﹣1)+m的图象经过第二、三、四象限,
则得到,
解得m=﹣.
14.(2014?梅州)已知直线y=kx+b,若k+b=﹣5,kb=6,那么该直线不经过第 一 象限.
【解答】解:∵k+b=﹣5,kb=6,
∴k<0,b<0,
∴直线y=kx+b经过二、三、四象限,即不经过第一象限.
故答案为:一.
15.(2015春?巴南区校级期末)已知函数y=(2m﹣2)x+m+1,
(1)m为何值时,图象过原点.
(2)已知y随x增大而增大,求m的取值范围.
(3)函数图象与y轴交点在x轴上方,求m取值范围.
(4)图象过二、一、四象限,求m的取值范围.
【解答】解:(1)∵函数图象过原点,
∴m+1=0,即m=﹣1;
(2)∵y随x增大而增大,
∴2m﹣2>0,解得m>1;
(3)∵函数图象与y轴交点在x轴上方,
∴m+1>0,即m>﹣1;
(4)∵图象过二、一、四象限,
∴,解得﹣1<m<1.
16.(2015秋?当涂县校级期中)已知一次函数y=(4﹣k)x﹣2k2+32
(1)k为何值时,y随x的增大而减小?
(2)k为何值时,它的图象经过原点?
【解答】解:(1)∵一次函数y=(4﹣k)x﹣2k2+32,y随x的增大而减小,
∴4﹣k<0
∴k>4;
(2)∵一次函数y=(4﹣k)x﹣2k2+32,它的图象经过原点,
∴﹣2k2+32=0
解得:k=±4
∵4﹣k≠0
∴k=﹣4.
考点6、一次函数的应用
1.小丽一家利用元旦三天驾车到某景点旅游。小汽车出发前油箱有油36L,行驶若干小时后,途中在加油站加油若干升。油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示。根据图象回答下列问题:
(1)小汽车行驶________h后加油, 中途加油__________L;
(2)求加油前油箱余油量Q与行驶时间t的函数关系式;
(3)如果加油站距景点200km,车速为80km/h,要到达目
的地,油箱中的油是否够用?请说明理由.
解:(1)3 ; 24
(2)设Q与t的函数关系式:Q=kt+b过(0、36),(3、6)
b=36
6=3k+b
k=-1
b=36
Q与t的函数关系式为:Q=-10t+36
(3)够用
到达目的地的时间t:200÷80=2.5(h)
需要油量: 2.5×10=25(L)
余油量30升 25<30
油箱中的油够用
2.在一次远足活动中,某班学生分成两组,第一组由甲地匀速步行到乙地后原路返回,第二组由甲地匀速步行经乙地继续前行到丙地后原路返回,两组同时出发,设步行的时间为t(h),两组离乙地的距离分别为S1(km)和S2(km),图中的折线分别表示S1、S2与t之间的函数关系.
(1)甲、乙两地之间的距离为 km,乙、丙两地之间的距离为 km;
(2)求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少?
(3)求图中线段AB所表示的S2与t间的函数关系式,并写出自变量t的取值范围.
解(1)8,2
(2)第二组由甲地出发首次到达乙地所用的时间为:[来源:Zxxk.Com]
(小时)
第二组由乙地到达丙地所用的时间为:
(小时)
(3)根据题意得A、B的坐标分别为(0.8,0)
和(1,2),设线段AB的函数关系式为:
,根据题意得:
解得:
∴图中线段AB所表示的S2与t间的函数关系式为:,自变量t的取值范围是:.
3.鞋子的“鞋码”和鞋长(cm)存在一种换算关系,下表是几组“鞋码”与鞋长换算的对应数值:[注:“鞋码”是表示鞋子大小的一种号码]
鞋长(cm)
16
19
21
24
鞋码(号)
22
28
32
38
(1)设鞋长为x,“鞋码”为y,试判断点(x,y)在你学过的哪种函数的图象上?
(2)求x、y之间的函数关系式;
(3)如果某人穿44号“鞋码”的鞋,那么他的鞋长是多少?
、解:(1)一次函数.
(2)设.
由题意,得
解得
∴.(x是一些不连续的值.一般情况下,x取16、16.5、17、17.5、…、26、26.5、27等)
(3)时,.
答:此人的鞋长为27cm.
4.某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件,可获利润150元,每制造一个乙种零件可获利润260元,在这20名工人中,车间每天安排x名工人制造甲种零件,其余工人制造乙种零件.
(1)请写出此车间每天所获利润y(元)与x(人)之间的函数关系式;
(2)若要使车间每天所获利润不低于24000元,你认为至少要派多少名工人去制造乙种零件才合适?
解:(1)此车间每天所获利润y(元)与x(人)之间的函数关系式是
y=6x·150+5(20-x)·260=26000-400x(0≤x≤20).
(2)当y≥24000时,有26000-400x≥24000,
∴x≤5,
∴20-x≥15.
∴要想使每天车间所获利润不低于24000元,至少要派15名工人去制造乙种零件才合适。
5.光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,现将这50台收割机派往A,B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见下表.
?
每台甲型收割机的租金
每台乙型收割机的租金
A地区
1800元
1600元
B地区
1600元
1200元
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x之间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分派方案,并将各种方案设计出来;
(1)派往A地区x台乙型联合收割机,则派往A地区(30-x)台甲型联合收割机,派往B地区(30-x)台乙型联合收割机,派往B地区20-(30-x)=x-10(台)甲型联合收割机.
∴y=1600x+120O(30-x)+180O(30-x)+1600(x-10)=20Ox+74000.
自变量x的取值范围是10≤x≤30(x是正整数),
(2)由题意得20Ox+74000≥7960O,∴x≥28.
∴x=28,29,30.
∴有3种不同分配方案.
①当x=28时,即派往A地区甲型联合收割机2台,乙型联合收割机28台,派往B地区甲型联合收割机18台,乙型联合收割机2台.
②当x=29时,即派往A地区甲型联合收割机1台,乙型联合收割机29台,派往B地区甲型联合收割机19台,乙型联合收割机1台.[来源:学科网ZXXK]
③当x=30时,即30台乙型联合收割机全部派往A地区,20台甲型联合收割机全部派往B地区.
6.辽南素有“苹果之乡”美称,某乡组织20辆汽车装运A、B、C三种苹果42吨到外地销售,按规定每辆车只装同一种苹果,且必须装满,每种苹果不少于2车。(1)设有x辆车装A种苹果,用y辆车装B种苹果,根据下表提供的信息求y与x的函数关系式,并求x的取值范围。
苹果的品种
A
B
C
每辆车运载量(吨)
2.2
2.1
2
每吨苹果获利(百元)
6
8
5
(2)设此次外销活动的利润为W(百元),求W与x的函数关系式及最大利润,并安排相应的车辆分配方案。
解:(1)由题意得,运C种苹果有(20-x-y)辆车,则2.2x+2.1y+2·(20-x-y)=42
∴y=-2x+20
∴运A种苹果有x辆汽车,运B种苹果有(-2x+20)辆汽车,运C种苹果有20-x-y=20-x-(20-2x)=x辆汽车
∴x为整数
∴x的取值范围是2≤x≤9,且x为整数
(2)W=2.2×6x+2.1×8(20-2x)+2×5x
∴W=-10.4x+336,∴-10.4<0,∴W随x的增大而减小,当x=2时,W有最大值为315.2,即最大利润为31520元。
二、课堂重难点题型精讲
题型1、一次函数的解析式
1.(2009?鄂州校级模拟)如图,已知点A的坐标为(0,1),点B的坐标为(,﹣2),点P在直线y=﹣x上运动,当|PA﹣PB|最大时点P的坐标为( )
A.(2,﹣2) B.(4,﹣4) C.(,﹣) D.(5,﹣5)
【解答】解:作A关于直线y=﹣x对称点C,易得C的坐标为(﹣1,0);连接BC,可得直线BC的方程为y=﹣x﹣;
求BC与直线y=﹣x的交点,可得交点坐标为(4,﹣4);
此时|PA﹣PB|=|PC﹣PB|=BC取得最大值,其他B C P不共线的情况,根据三角形三边的关系可得|PC﹣PB|<BC;
故答案为B.
2.(2012?洪山区校级模拟)已知点A(2a﹣1,3a+1),直线l经过点A,则直线l的解析式是 y=x+ .
【解答】解:∵点A的坐标为A(2a﹣1,3a+1),
∴,
由①得,a=,
由②得,a=,
所以=,
整理得,y=x+.
故答案为:y=x+.
3.(2005?黑龙江)一次函数y=kx+3的图象与坐标轴的两个交点之间的距离为5,则k的值为 或 .
【解答】解:在y=kx+3中令x=0,得y=3,
则函数与y轴的交点坐标是:(0,3);
设函数与x轴的交点坐标是(a,0),
根据勾股定理得到a2+32=25,
解得a=±4;
当a=4时,把(4,0)代入y=kx+3,得k=﹣;
当a=﹣4时,把(﹣4,0)代入y=kx+3,得k=.
故k的值为或.
4.(2011?辽阳)甲、乙两名自行车爱好者准备在一段长为3 500米的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面.他们同时出发,匀速前进,已知甲的速度为12米/秒,设甲、乙两人之间的距离为s(米),比赛时间为t(秒),图中的折线表示从两人出发至其中一人先到达终点的过程中s(米)与t(秒)的函数关系.根据图中信息,回答下列问题:
(1)乙的速度为 14 米/秒;
(2)当乙追上甲时,求乙距起点多少米.
(3)求线段BC所在直线的函数关系式.
【解答】解:(1)设乙的速度为x米/秒,
则300+150×12=150x,解得x=14,
故答案为:14;
(2)由图象可知乙用了150秒追上甲,
14×150=2 100(米).
∴当乙追上甲时,乙距起点2 100米;
(3)乙从出发到终点的时间为=250(秒),
此时甲、乙的距离为:
(250﹣150)(14﹣12)=200(米),
∴C点(250,200),
又B点坐标(150,0),
设BC所在直线的函数关系式为s=kt+b(k≠0,k,b为常数),
将B、C两点代入,得,解得,
∴BC所在直线的函数关系式为s=2t﹣300.
5.(2014春?武侯区校级月考)已知:一次函数y=kx+b的函数值随x的增大而减少,若已知自变量x的取值范围是﹣1≤x≤1,相应的函数值的取值范围是﹣3≤y≤﹣1,求函数解析式.
【解答】解:当k<0时,y随x的增大而减小,
把x=﹣1,y=﹣1;x=1,y=﹣3代入的解析式y=kx+b,
得
解得
∴一次函数解析式为y=﹣x﹣2.
题型2、一次函数图象上点的坐标的特征
1.(2012?巴中校级自主招生)如果一条直线l经过不同的三点A(a,b),B(b,a),C(a﹣b,b﹣a),那么直线l经过( )
A.第二、四象限 B.第一、二、三象限
C.第二、三、四象限 D.第一、三、四象限
【解答】解:设直线的解析式是y=kx+c,
把A(a,b),B(b,a),C(a﹣b,b﹣a)代入得:,
解得:k=﹣1,c=0,
∴y=﹣x,
∴图象经过第二、四象限,
故选A.
2.(2014?内江)如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、A2B3、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )
A. B. C. D.
【解答】解:∵A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,
∴依题意得:B1(1,2),B2(2,4),B3(3,6),…,Bn(n,2n)
∵A1B1∥A2B2,
∴△A1B1P1∽△A2B2P1,
∴=,
∴△A1B1P1与△A2B2P1对应高的比为:1:2,
∵A1A2=1,
∴A1B1边上的高为:,
∴=××2=,
同理可得:=,=,
∴Sn=.
故选:D.
3.(2013?江干区一模)已知两直线y1=kx+k﹣1、y2=(k+1)x+k(k为正整数),设这两条直线与x轴所围成的三角形的面积为Sk,则S1+S2+S3+…+S2013的值是( )
A. B. C. D.
【解答】解:∵方程组的解为,
∴两直线的交点是(﹣1,﹣1),
∵直线y1=kx+k﹣1与x轴的交点为(,0),y2=(k+1)x+k与x轴的交点为(,0),
∴Sk=×|﹣1|×|﹣|=|﹣|,
∴S1+S2+S3+…+S2013=×(1﹣+﹣+﹣+…+﹣)
=×(1﹣)
=×
=.
故选D.
4.(2015?宁德)如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2015的坐标是( )
A.(22014,22014) B.(22015,22015) C.(22014,22015) D.(22015,22014)
【解答】解:∵OA1=1,
∴点A1的坐标为(1,0),
∵△OA1B1是等腰直角三角形,
∴A1B1=1,
∴B1(1,1),
∵△B1A1A2是等腰直角三角形,
∴A1A2=1,B1A2=,
∵△B2B1A2为等腰直角三角形,
∴A2A3=2,
∴B2(2,2),
同理可得,B3(22,22),B4(23,23),…Bn(2n﹣1,2n﹣1),
∴点B2015的坐标是(22014,22014).
故选:A.
5.(2016春?秦皇岛期末)已知直线y=2x+8与x轴和y轴的交点的坐标分别是 (﹣4,0) 、 (0,8) ;与两条坐标轴围成的三角形的面积是 16 .
【解答】解:当y=0时,x=﹣4,
∴直线y=2x+8与x轴的交点坐标为(﹣4,0);
当x=0时,y=8,
∴直线y=2x+8与y轴的交点坐标为(0,8);
∴三角形的底是|﹣4|,高是8,
∴与两条坐标轴围成的三角形的面积是×|﹣4|×8=16.
故填(﹣4,0)、(0,8)、16.
6.(2013?广安)已知直线y=x+(n为正整数)与坐标轴围成的三角形的面积为Sn,则S1+S2+S3+…+S2012= .
【解答】解:令x=0,则y=,
令y=0,则﹣x+=0,
解得x=,
所以,Sn=??=(﹣),
所以,S1+S2+S3+…+S2012=(﹣+﹣+﹣+…+﹣)=(﹣)=.
故答案为:.
7.(2012?南通)无论a取什么实数,点P(a﹣1,2a﹣3)都在直线l上.Q(m,n)是直线l上的点,则(2m﹣n+3)2的值等于 16 .
【解答】解:∵令a=0,则P(﹣1,﹣3);再令a=1,则P(0,﹣1),由于a不论为何值此点均在直线l上,
∴设此直线的解析式为y=kx+b(k≠0),
∴,解得,
∴此直线的解析式为:y=2x﹣1,
∵Q(m,n)是直线l上的点,
∴2m﹣1=n,即2m﹣n=1,
∴原式=(1+3)2=16.
故答案为:16.
8.(2009?株洲)孔明同学在解方程组的过程中,错把b看成了6,他其余的解题过程没有出错,解得此方程组的解为,又已知直线y=kx+b过点(3,1),则b的正确值应该是 ﹣11 .
【解答】解:依题意将代入y=kx+6
得:2=﹣k+6,k=4;
将点(3,1)和k=4代入y=kx+b
得1=3×4+b,
∴b=﹣11.
9.(2015?东营)如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标是 (,) .
【解答】解:过B1向x轴作垂线B1C,垂足为C,
由题意可得:A(1,0),AO∥A1B1,∠B1OC=30°,
∴CB1=OB1cos30°=,
∴B1的横坐标为:,则B1的纵坐标为:,
∴点B1,B2,B3,…都在直线y=x上,
∴B1(,),
同理可得出:A的横坐标为:1,
∴y=,
∴A2(2,),
…
An(1+,).
∴A2015(,).
故答案为(,).
10.(2015?丹东)如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1A2B1、△A2A3B2、△A3A4B3…△AnAn+1Bn均为等边三角形,点A1、A2、A3…An+1在x轴的正半轴上依次排列,点B1、B2、B3…Bn在直线OD上依次排列,那么点Bn的坐标为 (3×2n﹣2,×2n﹣2) .
【解答】解:∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,
∵∠B1OA2=30°,
∴∠B1OA2=∠A1B1O=30°,可求得OA2=2OA1=2,
同理可求得OAn=2n﹣1,
∵∠BnOAn+1=30°,∠BnAnAn+1=60°,
∴∠BnOAn+1=∠OBnAn=30°
∴BnAn=OAn=2n﹣1,
即△AnBnAn+1的边长为2n﹣1,则可求得其高为×2n﹣1=×2n﹣2,
∴点Bn的横坐标为×2n﹣1+2n﹣1=×2n﹣1=3×2n﹣2,
∴点Bn的坐标为(3×2n﹣2,×2n﹣2).
故答案为(3×2n﹣2,×2n﹣2).
11.(2015?衡阳)如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA1=1,则OA2015的长为 22014 .
【解答】解:因为OA1=1,
∴OA2=2,OA3=4,OA4=8,
由此得出OAn=2n﹣1,
所以OA2015=22014,
故答案为:22014.
12.(2015?北海)如图,直线y=﹣2x+2与两坐标轴分别交于A、B两点,将线段OA分成n等份,分点分别为P1,P2,P3,…,Pn﹣1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn﹣1,用S1,S2,S3,…,Sn﹣1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn﹣1Pn﹣2Pn﹣1的面积,则当n=2015时,S1+S2+S3+…+Sn﹣1= .
【解答】解:∵P1,P2,P3,…,Pn﹣1是x轴上的点,且OP1=P1P2=P2P3=…=Pn﹣2Pn﹣1=,
分别过点p1、p2、p3、…、pn﹣2、pn﹣1作x轴的垂线交直线y=﹣2x+2于点T1,T2,T3,…,Tn﹣1,
∴T1的横坐标为:,纵坐标为:2﹣,
∴S1=×(2﹣)=(1﹣)
同理可得:T2的横坐标为:,纵坐标为:2﹣,
∴S2=(1﹣),
T3的横坐标为:,纵坐标为:2﹣,
S3=(1﹣)
…
Sn﹣1=(1﹣)
∴S1+S2+S3+…+Sn﹣1=[n﹣1﹣(n﹣1)]=×(n﹣1)=,
∵n=2015,
∴S1+S2+S3+…+S2014=××2014=.
故答案为:.
13.(2006?绍兴)如图,一次函数y=x+5的图象经过点P(a,b)和Q(c,d),则a(c﹣d)﹣b(c﹣d)的值为 25 .
【解答】解:由P(a,b),Q(c,d)两点在一次函数y=x+5的图象上,
则b=a+5,d=c+5,即:a﹣b=﹣5,c﹣d=﹣5.
所以a(c﹣d)﹣b(c﹣d)=(c﹣d)(a﹣b)=(﹣5)×(﹣5)=25.
14.(2016?鄂州)如图,直线l:y=﹣x,点A1坐标为(﹣3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2016的坐标为 (﹣,0) .
【解答】解:∵点A1坐标为(﹣3,0),
∴OA1=3,
∵在y=﹣x中,当x=﹣3时,y=4,即B1点的坐标为(﹣3,4),
∴由勾股定理可得OB1==5,即OA2=5=3×,
同理可得,
OB2=,即OA3==5×()1,
OB3=,即OA4==5×()2,
以此类推,
OAn=5×()n﹣2=,
即点An坐标为(﹣,0),
当n=2016时,点A2016坐标为(﹣,0).
故答案为:(﹣,0)
15.(2014?高青县模拟)直线y=x+2与x轴、y轴分别交于A、B两点,D是x轴上一点,坐标为(x,0),△ABD的面积为S.
(1)求点A和点B的坐标;
(2)求S与x的函数关系式;
(3)当S=12时,求点D的坐标.
【解答】解:(1)令y=0,则x+2=0,解得x=﹣4,
令x=0,则y=2,
所以,点A,B的坐标分别为(﹣4,0)和(0,2);
(2)∵A(﹣4,0),D(x,0),
∴AD=|x﹣(﹣4)|,
∴S=AD?OB=|x﹣(﹣4)|×2=|x+4|;
(3)∵S=12,
∴|x+4|=12,
即x+4=12或x+4=﹣12,
解得x=8或x=﹣16,
所以,D的坐标为(8,0)或(﹣16,0).
16.(2015春?自贡期末)点P(x,y)在直线x+y=8上,且x>0,y>0,点A的坐标为A(6,0),设△OPA的面积为S.
(1)求S与x的函数关系式,并直接写出x的取值范围;
(2)当S=9时,求点P的坐标.
【解答】解:(1)过点P作PB⊥x轴,垂足为B,
由三角形的面积公式可知:S==即:s=﹣3x+24.(0<x<8);
(2)将s=9代入s=﹣3x+24得:x=5,将x=5代入x+y=8得:y=3,
故点P的坐标为(5,3).
题型3、一次函数图象的几何变换
1.(2016春?云梦县期末)如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x﹣5上时,线段BC扫过的面积为( )
A.80 B.88 C.96 D.100
【解答】解:∵点A、B的坐标分别为(2,0)、(8,0),
∴AB=6,
∵∠CAB=90°,BC=10,
∴CA==8,
∴C点纵坐标为:8,
∵将△ABC沿x轴向右平移,当点C落在直线y=x﹣5上时,
∴y=8时,8=x﹣5,
解得:x=13,
即A点向右平移13﹣2=11个单位,
∴线段BC扫过的面积为:11×8=88.
故选:B.
2.(2015?白云区校级一模)把函数y=﹣2x+3的图象向左平移2个单位长度,再向下平移2个单位长度,可得到的图象的函数解析式是( )
A.y=﹣2x+7 B.y=﹣2x﹣7 C.y=﹣2x﹣3 D.y=﹣2x
【解答】解:把函数y=﹣2x+3的图象向左平移2个单位长度,再向下平移2个单位长度,可得到的图象的函数解析式是:y=﹣2(x+2)+3﹣2=﹣2x﹣3,
故选C.
3.(2010?黄石)将函数y=﹣6x的图象l1向上平移5个单位得直线l2,则直线l2与坐标轴围成的三角形面积为 .
【解答】解:由题意得l2的解析式为:y=﹣6x+5,
∴与y轴的交点为(0,5),
与x轴的交点为(,0),
∴所求三角形的面积=×5×=.
4.(2013?包头)如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D.若DB=DC,则直线CD的函数解析式为 y=﹣2x﹣2 .
【解答】解:设直线AB的解析式为y=kx+b,
把A(0,2)、点B(1,0)代入,得,
解得,
故直线AB的解析式为y=﹣2x+2;
将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D,使DB=DC,
∴DO垂直平分BC,
∴OC=OB,
∵直线CD由直线AB平移而成,
∴CD=AB,
∴点D的坐标为(0,﹣2),
∵平移后的图形与原图形平行,
∴平移以后的函数解析式为:y=﹣2x﹣2.
故答案为:y=﹣2x﹣2.
5.(2014秋?南京校级期末)如图,正比例函数y=kx(k≠0)的图象经过点A(2,4),AB⊥x轴于点B,将△ABO绕点A逆时针旋转90°得到△ADC,则直线AC的函数表达式为 y=﹣0.5x+5 .
【解答】解:∵正比例函数y=kx(k≠0)经过点A(2,4)
∴4=2k,
解得:k=2,
∴y=2x;
∵A(2,4),AB⊥x轴于点B,
∴OB=2,AB=4,
∵△ABO绕点A逆时针旋转90°得到△ADC,
∴DC=OB=2,AD=AB=4
∴C(6,2)
设直线AC的解析式为y=ax+b,
把(2,4)(6,2)代入解析式可得:,
解得:,
所以解析式为:y=﹣0.5x+5
6.(2011?咸宁)在平面直角坐标系中,点P从原点O出发,每次向上平移2个单位长度或向右平移1个单位长度.
(1)实验操作:
在平面直角坐标系中描出点P从点O出发,平移1次后,2次后,3次后可能到达的点,并把相应点的坐标填写在表格中:
P从点O出发平移次数
可能到达的点的坐标
1次
(0,2),(1,0)
2次
3次
(2)观察发现:
任一次平移,点P可能到达的点在我们学过的一种函数的图象上,如:平移1次后在函数 y=﹣2x+2 的图象上;平移2次后在函数 y=﹣2x+4 的图象上…由此我们知道,平移n次后在函数 y=﹣2x+2n 的图象上.(请填写相应的解析式)
(3)探索运用:
点P从点O出发经过n次平移后,到达直线y=x上的点Q,且平移的路径长不小于50,不超过56,求点Q的坐标.
【解答】解:(1)如图所示:
P从点O出发平移次数
可能到达的点
的坐标
1次
2次
(0,4),(1,2),(2,0)
3次
(0,6),(1,4),(2,2),(3,0)
(2)设过(0,2),(1,0)点的函数解析式为:y=kx+b(k≠0),
则,
解得,
故第一次平移后的函数解析式为:y=﹣2x+2;
∴答案依次为:y=﹣2x+2;y=﹣2x+4;y=﹣2x+2n.
(3)设点Q的坐标为(x,y),依题意,.
解这个方程组,得到点Q的坐标为.
∵平移的路径长为x+y,
∴50≤≤56.
∴37.5≤n≤42.
∵点Q的坐标为正整数,
∴n是3的倍数,n可以取39、42,
∴点Q的坐标为(26,26),(28,28).
7.(2010?顺义区二模)如图,在平面直角坐标系xOy中,A点的坐标为(1,2),B点的坐标为(2,1).
(1)求△OAB的面积;
(2)若△OAB沿直线向下平移,使点A落在x轴上,画出平移后的三角形,求平移的距离及平移过程中△OAB所扫过的面积.
【解答】解:(1)△OAB的面积等于正方形的面积﹣3个三角形的面积
=2×2﹣
=;
(2)
平移的距离=
△OAB所扫过的面积=2+=11.5.
8.(2014?六合区一模)已知一次函数y=x+b的图象与x轴,y轴交于点A、B.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b= 2 ;
(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值;
(3)当b>0时,函数y1=x+b图象绕点B逆时针旋转n°(0°<n°<180°)后,对应的函数关系式为
y=﹣x+b,求n的值.
【解答】解:(1)将y=x+b的图象沿x轴向右平移2个单位后得到y=x﹣2+b,
由题意,得0=0﹣2+b,
解得b=2.
故答案为2;
(2)∵当x=0时,y=4,
∴y2=kx+4图象与y轴交于点(0,4).
∵(0,4)关于y轴对称点就是本身,
∴(0,4)在函数y=x+b图象上.
∴b=4.
∴一次函数y1=x+4,它与x轴的交点坐标为(﹣4,0).
∵y2=kx﹣4的图象与y1=x+4的图象关于y轴对称,
∴y2=kx﹣4的图象经过点(4,0),则0=4k+4,
∴k=﹣1;
(3)∵当x=0时,y1=b,
∴y1=x+b图象与y轴交于点B(0,b).
∵当y1=0时,x=﹣b,
∴y1=x+b图象与x轴交于点A(﹣b,0).
如图,∵AO=BO=b(b>0),∴∠ABO=45°.
∵当y3=0时,x=,
∴y3=﹣x+b图象与x轴交于点C(,0).
如图,∵CO=,
∴tan∠ACB==,
∴∠ACB=60°.
∴n°=180°﹣∠ACB﹣∠BAC=75°.
即n的值为75.
题型4、一次函数与一元一次方程
1.(2015春?迁安市期末)如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则方程2x=ax+4的解集为( )
A.x= B.x=3 C.x=﹣ D.x=﹣3
【解答】解:∵A点在直线y=2x上,
∴3=2m,解得m=,
∴A点坐标为(,3),
∵y=2x,y=ax+4,
∴方程2x=ax+4的解即为两函数图象的交点横坐标,
∴方程2x=ax+4的解为x=,
故选A.
2.(2015秋?合肥校级期中)已知方程x+b=0的解是x=﹣2,下列可能为直线y=x+b的图象是( )
A. B. C. D.
【解答】解:∵方程x+b=0的解是x=﹣2,
∴直线y=x+b过点(﹣2,0),
∵直线y=x+b经过第一、三象限.
故选C.
3.(2014秋?常熟市校级期末)同一平面直角坐标系中,一次函数y=k1x+b的图象与一次函数y=k2x的图象如图所示,则关于x的方程k1x+b=k2x的解为( )
A.x=0 B.x=﹣1 C.x=﹣2 D.x=1
【解答】解:由函数图象,得两直线的交点坐标是(﹣1,﹣2),
k1x+b=k2x的解为x=﹣1,
故选:B.
4.(2014春?博白县期末)一次函数y=ax+b交x轴于点(﹣3,0),则关于x的方程ax+b=0的解是 x=﹣3 .
【解答】解:由题意可知:当x=﹣3时,函数值为0;
因此当x=﹣3时,ax+b=0,
即方程ax+b=0的解为:x=﹣3.
故答案为:x=﹣3.
5.(2014秋?淄川区期末)已知关于x的一元一次方程kx+b=0的解是x=﹣2,一次函数y=kx+b的图象与y轴交于点(0,2),则这个一次函数的表达式是 y=x+2 .
【解答】解:把x=﹣2代入kx+b=0得﹣2k+b=0,
把(0,2)代入y=kx+b得b=2,
所以﹣2k+2=0,解得k=1,
所以一次函数解析式为y=x+2.
故答案为y=x+2.
6.(2014秋?宁化县校级期中)一次函数y=kx+b(k≠0)中,x与y的部分对应值如下表
x
﹣2
﹣1
0
1
2
y
6
4
2
0
﹣2
那么,一元一次方程kx+b=0在这里的解为: x=1 .
【解答】解:根据上表中的数据值,当y=0时,x=1,
即一元一次方程kx+b=0的解是x=1.
故答案是:x=1.
7.(2014秋?海宁市校级月考)如图,直线l1:y=k1x+b与直线l2:y=k2x+c在同一平面直角坐标系中的图象如图所示,则关于x的方程k1x+b=k2x+c的解x= 1 .
【解答】解:∵直线y=k1x+b与直线y=k2x+c的交点坐标为(1,﹣2),
∴关于x的方程k1x+b=k2x+c的解为x=1.
故答案为1.
8.(2012?湖州)一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为 x=﹣1 .
【解答】解∵一次函数y=kx+b过(2,3),(0,1)点,
∴,
解得:,
一次函数的解析式为:y=x+1,
∵一次函数y=x+1的图象与x轴交于(﹣1,0)点,
∴关于x的方程kx+b=0的解为x=﹣1.
故答案为:x=﹣1.
9.(2012秋?滨海县期末)直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图,则关于x的方程:k1x+b=k2x的解为x= ﹣1 .
【解答】解:∵直线l1:y=k1x+b与直线l2:y=k2x交于点(﹣1,2),
∴关于x的方程:k1x+b=k2x的解为x=﹣1,
故答案为:﹣1.
10.(2014春?江西期末)如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:
(1)方程kx+b=0的解;
(2)式子k+b的值;
(3)方程kx+b=﹣3的解.
【解答】解:(1)如图所示,当y=0时,x=2.
故方程kx+b=0的解是x=2;
(2)根据图示知,该直线经过点(2,0)和点(0,﹣2),则
,
解得 ,
故k+b=1﹣2=﹣1,即k+b=﹣1;
(3)根据图示知,当y=﹣3时,x=﹣1.
故方程kx+b=﹣3的解是x=﹣1.
题型5、一次函数与二元一次方程组
1.(2012?南宁)如图,已知函数y=x﹣2和y=﹣2x+1的图象交于点P,根据图象可得方程组的解是 .
【解答】解:∵由图象可知:函数y=x﹣2和y=﹣2x+1的图象的交点P的坐标是(1,﹣1),
又∵由y=x﹣2,移项后得出x﹣y=2,
由y=﹣2x+1,移项后得出2x+y=1,
∴方程组的解是,
故答案为:.
2.(2013秋?平川区期末)如图,已知y=ax+b和y=kx的图象交于点P,根据图象可得关于x、y的二元一次方程组的解是 .
【解答】解:∵y=ax+b和y=kx的图象交于点P(﹣4,﹣2),
∴方程组的解是.
故答案为.
3.(2015秋?古田县月考)(1)求一次函y=2x﹣2的图象l1与y=x﹣1的图象l2的交点P的坐标.
(2)求直线l1与y轴交点A的坐标;求直线l2与x轴的交点B的坐标;
(3)求由三点P、A、B围成的三角形的面积.
【解答】解:(1)由解得:所以点P的坐标为(,﹣),
(2)当x=0时,由y=2×0﹣2=﹣2,所以点A坐标是(0,﹣2).
当y=0时,由0=﹣x﹣1,得x=2,所以点B坐标是(2,0).
(3)如图:连AB,
∴S△PAB=S△ABC﹣S△PBC=×2×1﹣××1=.
4.(2010秋?文成县校级期末)如图,L1,L2分别表示两个一次函数的图象,它们相交于点P,
(1)求出两条直线的函数关系式;
(2)点P的坐标可看作是哪个二元一次方程组的解;
(3)求出图中△APB的面积.
【解答】解:(1)设直线L1的解析式是y=kx+b,已知L1经过点(0,3),(1,0),
可得:,解得,
则函数的解析式是y=﹣3x+3;
同理可得L2的解析式是:y=x﹣2.
(2)点P的坐标可看作是二元一次方程组的解.
(3)易知:A(0,3),B(0,﹣2),P(,﹣);
∴S△APB=AB?|xP|=×5×=.
5.(2009?怀柔区二模)我们知道,在数轴上,x=1表示一个点,而在平面直角坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x﹣y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象,它也是一条直线,如图1.
观察图1可以得出:直线x=1与直线y=2x+1的交点P的坐标(1,3)就是
方程组的解,所以这个方程组的解为.
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它左侧的部分,如图②;y≤2x+1也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图3;
那么,所围成的区域就是图4中的阴影部分.
回答下列问题:
(1)在下面的直角坐标系中,用作图象的方法求出方程组的解;
(2)在右面的直角坐标系中用阴影表示,所围成的区域.
【解答】解:(1)在坐标系中分别作出直线x=2和直线,
这两条直线的交点是(2,0).
则x=2,y=0就是方程组的解.
(2)在(1)问的前提下作出y=﹣x2+2x+3的图象,
则所围成的区域如图阴影所示.
题型6、一次函数与一元一次不等式
1.(2013?潍坊二模)如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx﹣2的解集是( )
A.1<x<2 B.0<x<2 C.0<x<1 D.1<x
【解答】解:由于直线y1=kx+b过点A(0,2),P(1,m),
则有:,
解得 .
∴直线y1=(m﹣2)x+2.
故所求不等式组可化为:
mx>(m﹣2)x+2>mx﹣2,
不等号两边同时减去mx得,0>﹣2x+2>﹣2,
解得:1<x<2,
故选A.
2.(2015?黄冈中学自主招生)如图,表示阴影区域的不等式组为( )
A. B.
C. D.
【解答】解:∵x≥0表示直线x=0右侧的部分,2x+y≤5表示直线y=﹣2x+5左下方的部分,3x+4y≥9表示直线y=﹣x+右上方的部分,
故根据图形可知:满足阴影部分的不等式组为:.
故选D.
3.(2014春?通川区期末)如图,已知:函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是( )
A.x>﹣5 B.x>﹣2 C.x>﹣3 D.x<﹣2
【解答】解:∵函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),
则根据图象可得不等式3x+b>ax﹣3的解集是x>﹣2,
故选B.
4.(2011?鄂尔多斯)如图,直线y1=mx经过P(2,1)和Q(﹣4,﹣2)两点,且与直线y2=kx+b交于点P,则不等式kx+b>mx>﹣2的解集为 ﹣4<x<2 .
【解答】解:将P(2,1)代入解析式y1=mx得,1=2m,m=,
函数解析式为y=x,
将Q点纵坐标﹣2代入解析式得,﹣2=x,
x=﹣4,
则Q点坐标为(﹣4,﹣2).
kx+b>mx>﹣2的解集为y2>y1>﹣2时,x的取值范围为﹣4<x<2.
故答案为:﹣4<x<2.
5.(2015?甘南州)如图是一次函数的y=kx+b图象,则关于x的不等式kx+b>0的解集为 x>﹣2 .
【解答】解:由图可知:当x>﹣2时,y>0,即kx+b>0;
因此kx+b>0的解集为:x>﹣2.
6.(2015?德州校级二模)已知一次函数y=ax+b(a、b是常数,a≠0)函数图象经过(﹣1,4),(2,﹣2)两点,下面说法中:(1)a=2,b=2;(2)函数图象经过(1,0);(3)不等式ax+b>0的解集是x<1;(4)不等式ax+b<0的解集是x<1;正确的说法有 (2)(3) .(请写出所有正确说法的序号)
【解答】解:∵一次函数y=ax+b(a、b是常数,a≠0)函数图象经过(﹣1,4),(2,﹣2)两点,
∴,
解得a=﹣2,b=2,
∴一次函数的解析式为y=﹣2x+2,图象经过(1,0)点,
不等式﹣2x+b>0的解集为x<1,
不等式﹣2x+b<0的解集为x>1,
(1)错误.(2)正确,(3)正确,(4)错误.
故正确说法为(2)(3).
7.(2011?西宁)如图,直线y=kx+b经过A(﹣1,1)和B(﹣,0)两点,则关于x的不等式组0<kx+b<﹣x的解集为 ﹣<x<﹣1 .
【解答】解:∵直线y=kx+b经过B(﹣,0)点,
∴0<kx+b,就是y>0,y>0的范围在x轴的上方,
此时:﹣<x,
∵直线y=﹣x经过A(﹣1,1),
那么就是A点左侧kx+b<﹣x,
得:x<﹣1,
故不等式组0<kx+b<﹣x的解集为:﹣<x<﹣1.
故答案为:﹣<x<﹣1.
8.(2016春?十堰期末)如图所示,函数y=ax+b和y=|x|的图象相交于(﹣1,1),(2,2)两点.当y1>y2时,x的取值范围是 x<﹣1或x>2 .
【解答】解:∵函数y=ax+b和y=|x|的图象相交于(﹣1,1),(2,2)两点,
∴根据图象可以看出,当y1>y2时,x的取值范围是x>2或x<﹣1,
故答案为:x<﹣1或x>2.
9.(2015?辽宁校级模拟)如图所示,函数y1=|x|和y2=x+的图象相交于(﹣1,1),(2,2)两点.当y1>y2时,x的取值范围是 x<﹣1或x>2 .
【解答】解:当x≥0时,y1=x,又,
∴两直线的交点为(2,2),
y2=x+当x<0时,y1=﹣x,又y2=x+,
∴两直线的交点为(﹣1,1),
由图象可知:当y1>y2时x的取值范围为:x<﹣1或x>2.
故答案为:x<﹣1或x>2.
题型7、两直线的平行和相交问题
1.(2011?潮州校级模拟)直线y=﹣x+6和直线y=x﹣2与y轴围成的三角形的面积是( )
A.20 B.10 C.40 D.12
【解答】解:∵直线y=﹣x+6与y轴的交点为(0,6),直线y=x﹣2与y轴的交点分别为(0,﹣2),
∴两条直线与y轴交点之间距离为|6+2|=8,
由题意得,
解得,故两直线的交点坐标为(5,3),
∴两直线与y轴围成的三角形的面积=×8×5=20.
故选A.
2.已知直线y1=x,,,若无论x取何值,y总取y1、y2、y3中的最小值,则y的最大值为 .
【解答】解:如图,y的最小值在三条直线的公共部分所在的区域,∵y2与y3的交点最高,
∴y2=x+1,y3=﹣x+5的交点的y值最大,
联立得,,
解得,
∴y的最大值为.
故答案为:.
3.(2015?大连)在平面直角坐标系中,点A,B的坐标分别为(m,3),(3m﹣1,3),若线段AB与直线y=2x+1相交,则m的取值范围为 ≤m≤1 .
【解答】解:当y=3时,2x+1=3,解得x=1,
所以直线y=3与直线y=2x+1的交点为(1,3),
当点B在点A的右侧,则m≤1≤3m﹣1,解得≤m≤1;
当点B在点A的左侧,则3m﹣1≤1≤m,无解,
所以m的取值范围为≤m≤1.
4.(2004?西藏)已知,如图,直线y=8﹣2x与y轴交于点A,与x轴交于点B,直线y=x+b与y轴交于点C,与x轴交于点D,如果两直线交于点P,且AC:CO=3:5(AO>CO).
(1)求点A、B的坐标;
(2)求四边形COBP的面积S.
【解答】解:(1)∵直线y=8﹣2x与y轴交于点A,与x轴交于点B,
∴当x=0时,y=8﹣2×0=8,
当y=0时,x=4,
∴A(0,8),B(4,0);
(2)AC:CO=3:5,AO=8,
∴C(0,5),
∵直线y=x+b与y轴交于点C,
∴5=0+b,
b=5,
∴y=x+5,
,
解得:,
∴P(1,6),
∴四边形COBP的面积S=(5+6)×1+×3×6=.
5.(2015秋?沛县期末)如图,直线l1的函数表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
(1)图中点D的坐标为 (1,0) .
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上是否存在点P,使得△PDC的面积是△ADC面积的2倍?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【解答】解:(1)∵D在直线l1y=﹣3x+3的图象上,
∴当y=0时,0=﹣3x+3,
解得:x=1,
∴D(1,0),
故答案为:(1,0);
(2)设直线l2的解析表达式为y=kx+b,
∵过(3,﹣),(4,0),
∴,
解得,
∴直线l2的解析表达式为y=x﹣6;
(3)∵,解得:,
∴C(2,﹣3),
∴△ADC的面积为:×AD×3=×3×3=;
(4)存在,
∵△PDC的面积是△ADC面积的2倍,
∴△PDC的面积是9,
当P在第一象限时,△PDA面积为,
∴P点纵坐标为3,
∵P在直线l2上,
∴横坐标为6,
∴P(6,3);
当P在第三象限时,△DPA面积为,
∴P纵坐标为﹣9,
∵P在直线l2上,
∴横坐标为﹣2,
∴P(﹣2,﹣9);
综上:P(﹣2,﹣9)或(6,3).
6.(2015秋?深圳期末)如图,已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,与直线l2:y=﹣x交于点P.直线l3:y=﹣x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R.
(1)点A的坐标是 (﹣3,0) ,点B的坐标是 (0,3) ,点P的坐标是 (﹣2,1) ;
(2)将△POB沿y轴折叠后,点P的对应点为P′,试判断点P′是否在直线l3上,并说明理由;
(3)求△PQR的面积.
【解答】解:(1)∵直线l1:y=x+3与x轴交于点A,与y轴交于点B,
∴令y=0,求得x=﹣3,令x=0,求得y=3,
∴A(﹣3,0)、B(0,3),
∵直线l1与直线l2y=﹣x交于点P.
∴解得,
∴P(﹣2,1),
故答案为:(﹣3,0),(0,3),(﹣2,1);
(2)点P?在直线l3上
∵P(﹣2,1),且将△POB沿y轴折叠后,点P?与点P关于y轴对称,
∴P?(2,1),
当x=2时,代入y=﹣x+4得y=﹣×2+4=1,
∴点P?在直线l3上;
(3)分别过点P作PE⊥x轴于F,过点Q作QF⊥x轴于F,过点R作RG⊥x轴于G,
由 得,
∴Q(,),
由 得
∴R(4,﹣2),
对于y=﹣x+4,则y=0得x=,
∴C(,0),
∴S△AQC=AC×QF=×(+3)×=,S△OCR=OC?GR=××2=,S△AOP=OA?PE=×3×1=,
∴S△PQR=S△AQC+S△OCR﹣S△AOP=+﹣=.
7.(2015秋?建湖县期末)如图,直线l1:y1=kx+2(k≠0)与直线l2:y2=4x﹣4交于点P(m,4),直线l1分别交x轴、y轴于点A、B,直线l2交x轴于点C.
(1)求k、m的值;
(2)写出使得不等式kx+2<4x﹣4成立的x的取值范围;
(3)在直线l2上找点Q,使得S△QAC=S△BPC,求点Q的坐标.
【解答】解:(1)把P(m,4)代入y2=4x﹣4得4m﹣4=4,解得m=2,
所以P点坐标为(2,4),
把P(2,4)代入y1=kx+2得2k+2=4,解得k=1;
(2)当x>2时,kx+2<4x﹣4;
(3)当y=0时,x+2=0,解得x=﹣2,则A(﹣2,0);当x=0时,y1=x+2=2,则B(0,2),
当y=0时,4x﹣4=0,解得x=1,则C(1,0),
所以S△BPC=S△PAC﹣S△BAC=×(1+2)×4﹣×(1+2)×2=3,
设Q点坐标为(t,4t﹣4),
因为S△QAC=S△BPC=3,
所以×(1+2)×|4t﹣4|=3,解得t=或t=,
所以Q点的坐标为(,2)或(,2).
8.(2015秋?重庆校级期中)如图,在平面直角坐标系中,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B的坐标为(18,6).在x轴上有一点P(a,0),过点P作x轴的垂线分别交直线l1、l2于点C、D,直线l2与x轴交于点E.
(1)求直线l1、l2的表达式;
(2)若线段CD长为15,求此时a的值;
(3)若S△OBD=,求此时点P的坐标.
【解答】解:(1)设直线l1的表达式为y=k1x,
∵过点B(18,6),
∴18k1=6,
解得:k1=,
∴直线l1的表达式为y=x;
设直线l2的表达式为y=k2x+b,
∵过点A (0,24),B(18,6)
∴,解得:k2=﹣1,b=24,
∴直线l2的表达式y=﹣x+24;
(2)∵在x轴上有一点P(a,0),过点P作x轴的垂线分别交直线l1、l2于点C、D,
∴点C坐标为(a,a),点D坐标为(a,﹣a+24),
∴a﹣(﹣a+24)=15或﹣a+24﹣a=15,
解得:a=或a=;
(3)设点P(a,0),
由题意:××24×18=×24×18﹣×24×a,或××24×18=×24×a﹣×24×18,
解得a=1.8 或a=﹣(舍弃)
所以P点坐标为(﹣1.8,0).
题型8、与一次函数有关的几何动点问题
1.(2012?金东区一模)已知:如图,直线y=kx+b与x轴交于点A(8,0),与y轴交于点B(0,16),与直线y=x相交于点C.P(0,t)是y轴上的一个动点,过点P作直线l垂直y轴,与直线y=x相交于点D,与直线y=kx+b相交于点E,在直线l下方作一个等腰直角三角形DEF,使DF=DE,∠EDF=90°.
(1)求直线AB的解析式和C点的坐标;
(2)当点F落在x轴上时,求t的值;
(3)当t为何值时,以A,E,P,F为顶点的四边形是梯形?
【解答】解:(1)∵直线y=kx+b与x轴交于点A(8,0),与y轴交于点B(0,16),
∴,
解得,
所以,直线AB的解析式为y=﹣2x+16,
联立,
解得,
所以,C点坐标为(,);
(2)根据题意,点D、E的纵坐标都是t,
所以,﹣2x+16=t,
解得x=,
所以,点D(t,t),E(,t),
DE=|﹣t|,
∵点F在x轴上,
∴|﹣t|=t,
即﹣t=t或﹣t=﹣t,
解得t=或t=16,
所以,t的值为,16;
(3)①PE∥AF时,点F在x轴上,根据(2)的结论,
t=或16,
当t=16时,P、B、E三点重合,以A,E,P,F为顶点的是三角形,不符合题意舍去,
所以,t=;
②PF∥AE时,点D在点E的左边,
∵D(t,t),E(,t),
∴DE=﹣t=,
点F的纵坐标为:t﹣=,
∴点F(t,),
设直线PF的解析式为y=ex+f,
则,
解得,
所以,直线PF的解析式为y=x+t,
∵PF∥AE,
∴=﹣2,
解得t=;
③AP∥EF时,(i)若点P在y轴正半轴,则DE=t﹣=,
点F的纵坐标为t﹣=,
∴点F的坐标为(t,),
设直线EF的解析式为y=cx+d,则,
解得,
∴直线EF的解析式为y=﹣x+,
又∵A(8,0),P(0,t),
∴直线AP的解析式为y=﹣+t,
∵AP∥EF,
∴﹣=﹣1,
解得t=8,
(ii)若点P在y轴负半轴,则DE=﹣t=,
点F的纵坐标为t﹣=,
∴点F的坐标为(t,),
设直线EF的解析式为y=mx+n,则,
解得,
∴直线EF的解析式为y=x+,
又∵A(8,0),P(0,t),
∴直线AP的解析式为y=﹣+t,
∵AP∥EF,
∴﹣=1,
解得t=﹣8,
综上所述,t的值为,,8,﹣8.
2.(2016春?惠安县期末)如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x﹣2与x轴、y轴分别交于点E、F.
(1)求:①点D的坐标;
②经过点D,且与直线FC平行的直线的函数表达式;
(2)直线y=x﹣2上是否存在点P,使得△PDC为等腰直角三角形?若存在,求出点P 的坐标;若不存在,请说明理由.
(3)在平面直角坐标系内确定点M,使得以点M、D、C、E为顶点的四边形是平行四边形,请直接写出点M的坐标.
【解答】解:(1)①设点C的坐标为(m,2),
∵点C在直线y=x﹣2上,
∴2=m﹣2,
∴m=4,
即点C的坐标为(4,2),
∵四边形ABCD是矩形,
∴AB=CD=3,AD=BC=2,
∴点D的坐标为(1,2);
②设经过点D且与FC平行的直线函数表达式为y=x+b,
将D(1,2)代入y=x+b,得b=1,
∴经过点D且与FC平行的直线函数表达式为y=x+1;
(2)存在.
∵△EBC为等腰直角三角形,
∴∠CEB=∠ECB=45°,
又∵DC∥AB,
∴∠DCE=∠CEB=45°,
∴△PDC只能是以P、D为直角顶点的等腰直角三角形,
如图,①当∠D=90°时,延长DA与直线y=x﹣2交于点P1,
∵点D的坐标为(1,2),
∴点P1的横坐标为1,
把x=1代入y=x﹣2得,y=﹣1,
∴点P1(1,﹣1);
②当∠DPC=90°时,作DC的垂直平分线与直线y=x﹣2的交点即为点P2,
所以,点P2的横坐标为=,
把x=代入y=x﹣2得,y=,
所以,点P2(,),
综上所述,符合条件的点P的坐标为(1,﹣1)或(,);
(3)当y=0时,x﹣2=0,
解得x=2,
∴OE=2,
∵以点M、D、C、E为顶点的四边形是平行四边形,
∴若DE是对角线,则EM=CD=3,
∴OM=EM﹣OE=3﹣2=1,
此时,点M的坐标为(﹣1,0),
若CE是对角线,则EM=CD=3,
OM=OE+EM=2+3=5,
此时,点M的坐标为(5,0),
若CD是对角线,则平行四边形的中心坐标为(,2),
设点M的坐标为(x,y),
则=,=2,
解得x=3,y=4,
此时,点M的坐标为(3,4),
综上所述,点M的坐标为(﹣1,0),(5,0)(3,4).
3.(2015?泰州)已知一次函数y=2x﹣4的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为d1、d2.
(1)当P为线段AB的中点时,求d1+d2的值;
(2)直接写出d1+d2的范围,并求当d1+d2=3时点P的坐标;
(3)若在线段AB上存在无数个P点,使d1+ad2=4(a为常数),求a的值.
【解答】解:(1)对于一次函数y=2x﹣4,
令x=0,得到y=﹣4;令y=0,得到x=2,
∴A(2,0),B(0,﹣4),
∵P为AB的中点,
∴P(1,﹣2),
则d1+d2=3;
(2)①d1+d2≥2;
②设P(m,2m﹣4),
∴d1+d2=|m|+|2m﹣4|,
当0≤m≤2时,d1+d2=m+4﹣2m=4﹣m=3,
解得:m=1,此时P1(1,﹣2);
当m>2时,d1+d2=m+2m﹣4=3,
解得:m=,此时P2(,);
当m<0时,不存在,
综上,P的坐标为(1,﹣2)或(,);
(3)设P(m,2m﹣4),
∴d1=|2m﹣4|,d2=|m|,
∵P在线段AB上,
∴0≤m≤2,
∴d1=4﹣2m,d2=m,
∵d1+ad2=4,
∴4﹣2m+am=4,即(a﹣2)m=0,
∵有无数个点,
∴a=2.
4.(2015?温州模拟)如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0)、(12,6),直线y=﹣x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
(1)若直线y=﹣x+b平分矩形OABC的面积,求b的值;
(2)在(1)的条件下,当直线y=﹣x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
(3)在(1)的条件下,将矩形OABC沿DE折叠,若点O落在边BC上,求出该点坐标;若不在边BC上,求将(1)中的直线沿y轴怎样平移,使矩形OABC沿平移后的直线折叠,点O恰好落在边BC上.
【解答】解:(1)∵直线y=﹣x+b平分矩形OABC的面积,
∴其必过矩形的中心
由题意得矩形的中心坐标为(6,3),
∴3=﹣×6+b
解得b=12;
(2)如图1假设存在ON平分∠CNM的情况
①当直线PM与边BC和边OA相交时,过O作OH⊥PM于H
∵ON平分∠CNM,OC⊥BC,
∴OH=OC=6
由(1)知OP=12,
∴∠OPM=30°
∴OM=OP?tan30°=
当y=0时,由﹣x+12=0解得x=8,
∴OD=8
∴DM=8﹣;
②当直线PM与直线BC和x轴相交时
同上可得DM=8+(或由OM=MN解得);
(3)如图2假设沿DE将矩形OABC折叠,点O落在边BC上O′处连接PO′、OO′,则有PO′=OP
由(1)得BC垂直平分OP,∴PO′=OO′
∴△OPO′为等边三角形,∴∠OPD=30°
而由(2)知∠OPD>30°
所以沿DE将矩形OABC折叠,点O不可能落在边BC上;
如图3设沿直线y=﹣x+a将矩形OABC折叠,点O恰好落在边BC上O′处
连接P′O′、OO′,则有P′O′=OP′=a
由题意得:CP′=a﹣6,∠OPD=∠CO′O
在Rt△OPD中,tan∠OPD=
在Rt△OAO′中,tan∠CO′O=
∴=,即=,CO′=9
在Rt△CP′O′中,由勾股定理得:(a﹣6)2+92=a2
解得a=,12﹣=
所以将直线y=﹣x+12沿y轴向下平移个单位得直线y=﹣x+,将矩形OABC沿直线y=﹣x+折叠,点O恰好落在边BC上.
5.(2015?上虞区一模)如图1,平面直角坐标系中,已知A(0,4),B(5,0),D(3,0),点P从点A出发,沿y轴负方向在y轴上以每秒1个单位长度的速度匀速运动,过点P作PE∥x轴交直线AD于点E.
(1)设点P的运动时间为t(s),DE的单位长度为y,求y关于t的函数关系式,并写出t的取值范围;
(2)当t为何值时,以EP为半径的⊙E恰好与x轴相切?并求此时⊙E的半径;
(3)在点P的运动过程中,当以D,E,P三点为顶点的三角形是等腰三角形时,求此时t的值;
(4)如图2,将△ABD沿直线AD翻折,得到△AB′D,连结B′O,如果∠AOE=∠BOB′,求t值.(直接写出答案,不要求解答过程).
【解答】解:(1)∵A(0,4),B(5,0),D(3,0),
∴OA=4,OD=3,
由勾股定理得:AD==5,
①当0≤t≤4时,
∵PE∥x轴,
∴=,
∴=,
∴AE=t,
∴DE=5﹣t,
即y=5﹣t(0≤t≤4);
②当t>4时,y=t﹣5(t>4);
综上所述,y关于t的函数关系式为y=5﹣t(0≤t≤4),或y=t﹣5(t>4);
(2)作EM⊥OD于M,如图1所示:
则EM=4﹣t,
∵PE∥OD,
∴,
即,
解得:PE=t,AE=t,
当以EP为半径的⊙E恰好与x轴相切时,PE=EM,分两种情况:
①当0<t<4时,t=4﹣t,
解得:t=,此时PE=;
②当t>4时,t=t﹣4,
解得:t=16,此时12;
综上所述,当t为或16时,以EP为半径的⊙E恰好与x轴相切,⊙E的半径为或12;
(3)当0≤t≤4时,由PE=DE,
∴t=5﹣t,
解得:t=;
当t>4时,分三种情况:如图2所示:
①当DP=DE=t﹣5时,
由勾股定理得:OP2+OD2=DP2,
即(t﹣4)2+32=(t﹣5)2,
解得:t=8;
②当PE=PD时,
由勾股定理得:(t﹣4)2+32=(t)2,
解得:t=,或t=4(舍去);
∴t=;
③当PE=DE时,t=t﹣5
解得:t=10;
综上所述:当以D,E,P三点为顶点的三角形是等腰三角形时,t的值为或8或或10;
(4)设AD交BB′于F,连接BB′,如图3所示:
则AF⊥BB′,
∴∠AOD=∠BFD=90°,
又∵∠ADO=∠FDB,
∴∠OAD=∠FBD,△AOD∽△BFD,
∴,即,
∴BF=,
∴BB′=2BF=,
∵∠AOE=∠BOB′,∠OAD=∠FBD,
∴△AOE∽△BOB′,
∴,即,
∴AE==t,
∴t=.
6.(2015秋?宜兴市期末)如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=x相交于点A.
(1)求A点坐标;
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,则P点坐标是 (0,) ;
(3)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
【解答】解:(1)解方程组:得:
∴A点坐标是(2,3);
(2)设P点坐标是(0,y),
∵△OAP是以OA为底边的等腰三角形,
∴OP=PA,
∴22+(3﹣y)2=y2,
解得y=,
∴P点坐标是(0,),
故答案为(0,);
(3)存在;
由直线y=﹣2x+7可知B(0,7),C(,0),
∵S△AOC=××3=<6,S△AOB=×7×2=7>6,
∴Q点有两个位置:Q在线段AB上和AC的延长线上,设点Q的坐标是(x,y),
当Q点在线段AB上:作QD⊥y轴于点D,如图①,则QD=x,
∴S△OBQ=S△OAB﹣S△OAQ=7﹣6=1,
∴OB?QD=1,即×7x=1,
∴x=,
把x=代入y=﹣2x+7,得y=,
∴Q的坐标是(,),
当Q点在AC的延长线上时,作QD⊥x轴于点D,如图②则QD=﹣y,
∴S△OCQ=S△OAQ﹣S△OAC=6﹣=,
∴OC?QD=,即××(﹣y)=,
∴y=﹣,
把y=﹣代入y=﹣2x+7,解得x=,
∴Q的坐标是(,﹣),
综上所述:点Q是坐标是(,)或(,﹣).
7.(2014?新疆)如图,直线y=﹣x+8与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s)(0<t≤3).
(1)写出A,B两点的坐标;
(2)设△AQP的面积为S,试求出S与t之间的函数关系式;并求出当t为何值时,△AQP的面积最大?
(3)当t为何值时,以点A,P,Q为顶点的三角形与△ABO相似,并直接写出此时点Q的坐标.
【解答】解:(1)令y=0,则﹣x+8=0,
解得x=6,
x=0时,y=y=8,
∴OA=6,OB=8,
∴点A(6,0),B(0,8);
(2)在Rt△AOB中,由勾股定理得,AB===10,
∵点P的速度是每秒2个单位,点Q的速度是每秒1个单位,
∴AP=2t,
AQ=AB﹣BQ=10﹣t,
∴点Q到AP的距离为AQ?sin∠OAB=(10﹣t)×=(10﹣t),
∴△AQP的面积S=×2t×(10﹣t)=﹣(t2﹣10t)=﹣(t﹣5)2+20,
∵﹣<0,0<t≤3,
∴当t=3时,△AQP的面积最大,S最大=﹣(3﹣5)2+20=;
(3)若∠APQ=90°,则cos∠OAB=,
∴=,
解得t=,
若∠AQP=90°,则cos∠OAB=,
∴=,
解得t=,
∵0<t≤3,
∴t的值为,
此时,OP=6﹣2×=,
PQ=AP?tan∠OAB=(2×)×=,
∴点Q的坐标为(,),
综上所述,t=秒时,以点A,P,Q为顶点的三角形与△ABO相似,此时点Q的坐标为(,).
8.(2014?新余模拟)如图,在平面直角坐标系中,直线AB分别与x轴、y轴相交于A,B两点,OA、OB的长分别是方程x2﹣14x+48=0的两根,且OA<OB.
(1)求点A,B的坐标.
(2)过点A作直线AC交y轴于点C,∠1是直线AC与x轴相交所成的锐角,sin∠1=,求直线AC的解析式.
(3)若点M(m,m﹣5)在△AOC的内部,求m的取值范围.
【解答】解:(1)因式分解得,(x﹣6)(x﹣8)=0,
所以,x﹣6=0,x﹣8=0,
解得x1=6,x2=8,
∵OA<OB,
∴OA=6,OB=8,
∴点A(6,0),B(0,8);
(2)∵sin∠1=,∠1=∠COA,
∴设OC=3k,AC=5k,
由勾股定理得,OC2+OA2=AC2,
即(3k)2+62=(5k)2,
解得k=,
∴OC=3k=3×=,
∴点C(0,﹣),
设直线AC的解析式为y=kx+b,
则,
解得,
所以,直线AC的解析式为y=x﹣;
(3)∵点M(m,m﹣5)在△AOC的内部,
∴,
解不等式①得,m<5,
解不等式②得,m>2,
∴m的取值范围2<m<5.
9.(2013?维扬区校级二模)如图,已知直线y=x+4与x轴、y轴分别相交于点A、B,点C从O点出发沿射线OA以每秒1个单位长度的速度匀速运动,同时点D从A点出发沿AB以每秒1个单位长度的速度向B点匀速运动,当点D到达B点时C、D都停止运动.点E是CD的中点,直线EF⊥CD交y轴于点F,点E′与E点关于y轴对称.点C、D的运动时间为t(秒).
(1)当t=1时,AC= 2 ,点D的坐标为 (,) ;
(2)设四边形BDCO的面积为S,当0<t<3时,求S与t的函数关系式;
(3)当直线EF与△AOB的一边垂直时,求t的值;
(4)当△EFE′为等腰直角三角形时,直接写出t的值.
【解答】解:(1)如图1,过D作DH⊥AC于H,
∵直线y=x+4与x轴、y轴分别相交于点A,A、B,
∴A(﹣3,0),B(0,4),
∴AO=3,BO=4,
∴AB===5,
当0≤t≤3时,如图1,
∵CO=t,AD=t,
∴AC=3﹣t,DH=AD?sin∠BAO=t,AH=ADcos∠BAO=t,
当t=1时,AC=3﹣1=2,
点D的坐标为(,);
(2)∵AO=3,BO=4,AB=5
∴sin∠BAO==,cos∠BAO==
过D作DH⊥AC于H,
当0≤t≤3时,如图1,
∵CO=t,AD=t,
∴AC=3﹣t,DH=AD?sin∠BAO=t,
∴S=S△ABO﹣S△ADC=×3×4﹣?(3﹣t)?t,
S=t2﹣t+6(0<t<3).
(3)如图2,当EF⊥BO时,
∵EF⊥CD,
∴CD∥BO,
∴∠ACD=90°,
在Rt△ADC中,=cos∠BAO,
∴=,
t=,
当EF⊥AB时,如图3,
∵EF⊥CD,
∴直线CD和直线AB重合,
∴C点和A点重合,
∴t=3.
(4)①如图4,
当0<t<,且且重叠部分为等腰梯形PEQM时,
则∠PEQ=∠MQE,
∵菱形CDMN,
∴CD∥MN,
∴∠MQE=∠CEQ,
∵EF⊥CD,
即∠CEF=90°,
∴∠CEQ=45°,
∴∠ACD=∠CEQ=45°,
过D作DH⊥AC于H,则△DHC是等腰直角三角形,
∴DH=HC,
∴t=3﹣t﹣t,
∴t=;
②如图5,
当<t<5,且重叠部分为等腰梯形EHNK时,
同理可得∠CHE=45°,
连接DHDH,
∵EF垂直平分CD,
∴CH=DH,∠DHE=∠CHE=45°,
∴∠DHC=90°,
∴DH=t,
而CH=CO﹣HO=CO﹣(AO﹣AH)=t﹣(3﹣t),
∴t﹣(3﹣t)=t,
∴t=.
10.(2013?莆田模拟)阅读下面材料,并解决问题:
(I)如图4,等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5.则∠APB= 150° ,由于PA,PB不在一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌ △ABP .这样,就可以利用全等三角形知识,将三条线段的长度转化到一个三角形中从而求出∠APB的度数.
(II)(拓展运用)已知△ABC三边长a,b,c满足.
(1)试判断△ABC的形状 等腰直角三角形
(2)如图1,以点A为原点,AB所在直线为x轴建立平面直角坐标系,直接出点B,C的坐标 B(12,0),C(6,6) ;
(3)如图2,过点C作∠MCN=45°交AB于点M,N.请证明AM2+BN2=MN2;
(4)在(3)的条件下,若点N的坐标是(8,0),则点M的坐标为 (3,0) ;此时MN= 5 .并求直线CM的解析式.
(5)如图3,当点M,N分布在点B异侧时.则(3)中的结论还成立吗?
【解答】解:(Ⅰ)∵△ABC是等边三角形,
∴∠BAC=60°,
∵△ABP绕顶点A旋转到△ACP′处,
∴△ACP′≌△ABP,
∴P′A=PA=3,PB=P′C=4,∠PAP′=∠BAC=60°,
∴△APP′是等边三角形,
∴∠AP′P=60°,PP′=PA=3,
在△P′PC中,P′P2+P′C2=32+42=25=PC2,
∴∠PP′C=90°,
∴∠APB=∠AP′C=∠AP′P+∠PP′C=60°+90°=150°,
∴∠APB=150°;
故答案是:150°,△ABP;
(Ⅱ)(1)整理得,|a﹣6|+(c﹣12)2+=0,
由非负数的性质得,a﹣6=0,c﹣12=0,b﹣6=0,
解得a=b=6,c=12,
∵a2+b2=(6)2+(6)2=144=c2,
∴△ABC是直角三角形,
又∵a=b,
∴△ABC是等腰直角三角形;
(2)∵AB=c=12,
∴点B(12,0),
过点C作CD⊥x轴于D,则AD=CD=AB=×12=6,
∴点C的坐标为(6,6);
(3)如图,把△ACM绕点C逆时针旋转90°得到△BCM′,连接M′N,
由旋转的性质得,AM=BM′、CM=CM′、∠CAM=∠CBM′=45°,∠ACM=∠BCM′,
∴∠M′BN=∠ABC+∠CBN′=45°+45°=90°,
∵∠MCN=45°,
∴∠M′CN=∠BCN+∠BCM′=∠BCN+∠ACM=90°﹣∠MCN=90°﹣45°=45°,
∴∠MCN=∠M′CN,
在△MCN和△M′CN中,
,
∴△MCN≌△M′CN(SAS),
∴MN=M′N,
在Rt△M′NB中,BM′2+BN2=M′N2,
∴AM2+BN2=MN2;
(4)设AM=x,
∵点N的坐标是(8,0),
∴AN=8,BN=12﹣8=4,
∴MN=8﹣x,
由(3)的结论,x2+42=(8﹣x)2,
解得x=3,
∴AM=3,MN=8﹣3=5,
∴点M的坐标(3,0);
设直线CM的解析式为y=kx+b,
∵点C(6,6),M(3,0),
∴,
解得,
∴设直线CM的解析式为y=2x﹣6;
(5)如图,∵△ABC是等腰直角三角形,
∴∠CAB=∠CBA=45°,
把△BCN绕点C顺时针旋转90°得到△ACN′,
由旋转的性质得,AN′=BN,CN′=CN,∠CAN′=∠CBN=135°,
∴∠MAN′=135°﹣45°=90°,
∴点N′在y轴上,
∵∠MCN=45°,
∴∠MCN′=90°﹣45°=45°,
∴∠MCN=∠MCN′,
在△MCN和△MCN′中,
,
∴△MCN≌△MCN′(SAS),
∴MN=MN′,
在Rt△AMN′中,AM2+AN′2=MN′2,
∴AM2+BN2=MN2.
故答案为:(Ⅰ)150°,△ABP;(1)等腰直角三角形;(2)B(12,0),C(6,6);(4)(3,0),5.
11.(2013秋?镇江月考)如图,直线l1的解析表达式为:y=3x﹣3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
(1)求△ADC的面积;
(2)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,则点P的坐标为 (6,﹣3) ;
(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、D、C、H为顶点的四边形是平行四边形?若存在,请直接写出点H的坐标;若不存在,请说明理由.
【解答】解:(1)令y=0,则3x﹣3=0,
解得x=1,
∴点D(1,0),
∴AD=4﹣1=3,
设直线l2的解析式为y=kx+b(k≠0),
则,
解得,
∴设直线l2的解析式为y=﹣x+6,
联立,
解得,
∴点C的坐标为(2,3),
∴△ADC的面积=×3×3=;
(2)∵△ADP与△ADC的面积相等,点P是异于点C的点,
∴点P的纵坐标为﹣3,
∴﹣x+6=﹣3,
解得x=6,
∴点P(6,﹣3);
故答案为:(6,﹣3);
(3)①AC是平行四边形的对角线时,CH=AD=3,
点H的横坐标为2+3=5,
所以,点H的坐标为(5,3),
②CD是平行四边形的对角线时,CH=AD=3,
点H的横坐标是2﹣3=﹣1,
所以,点H的坐标为(﹣1,3),
③AD是对角线时,AD=,
所以,AD的中点坐标为(,0),
∵平行四边形的对角线互相平分,
∴设点H(x,y),则=,=0,
解得x=3,y=﹣3,
∴点H的坐标为(3,﹣3),
综上所述,存在点H(5,3)或(﹣1,3)或(3,﹣3),使以A、D、C、H为顶点的四边形是平行四边形.
12.(2009?随州)如图1,在Rt△A′OB′中,∠B′A′0=90°,A′,B′两点的坐标分别为(2,﹣1)和(0,﹣5),将A′0B′绕点O逆时针方向旋转90°,使OB’落在x轴正半轴上,得△AOB,点A′的对应点是A,点B’的对应点是B.
(1)写出A,B两点的坐标,并求直线AB的解析式;
(2)如图2,将△A0B沿垂直于x轴的线段CD折叠,(点C在x轴上,且不与点B重合,点D在线段AB上),使点B落在x轴上,对应点为点E,设点C的坐标为(x,0).
①当x为何值时,线段DE平分△AOB的面积;
②是否存在这样的点使得△AED为直角三角形?若存在,求出点C的坐标;若不存在,请说明理由.
③设△CDE与△AOB重叠部分的面积为S,直接写出S与点C的横坐标x之间的函数关系式(包括自变量x的取值范围).
【解答】解:(1)A(1,2),B(5,0),
设直线AB的解析式为y=kx+b,则有:
,
解得:,
∴直线AB的解析式为y=﹣x+.
(2)①当x=时,CD=y==,S△DEB=×5×=>3,
∴点E在O的右边.
由题意,得:S△DEB=×2(5﹣x)×=,x=5+(舍去),
∴x=5﹣.
②当∠ADE=90°时,得∠DBE=∠DEB=45°,舍去,
当∠EAD=90°时,点E与点O重合,得x=.
当∠AED=90°时,作AH⊥OB于H,证明△AHE∽△ECD,可得HE=1.
∴OE=2.
∴2+2(5﹣x)
同课章节目录
