破题致胜——期末复习检测高二数学:第一章常用逻辑用语1.1命题及其关系
文档属性
| 名称 | 破题致胜——期末复习检测高二数学:第一章常用逻辑用语1.1命题及其关系 |  | |
| 格式 | zip | ||
| 文件大小 | 597.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-04 08:29:46 | ||
图片预览



文档简介
复习指导
考点一:命题
例题:
1.设α和β为不重合的两个平面,给出下列命题: (1)若α内的两条相交直线分别平行于α内的两条直线,则α平行于β; (2)若α外一条直线l与α内的一条直线平行,则l和α平行; (3)设α和β相交于直线l,若β内有一条直线垂直于l,则β和β垂直; (4)直线l与β垂直的充分必要条件是l与α内的两条直线垂直. 上面命题中,真命题的序号是________. (写出所有真命题的序号)
【答案】 (1) (2).
2.下列命题是真命题的是( )
(1)若,则
(2)若,则
(3)函数有且仅有一个零点
(4)数列的前项和,则数列为等差数列
A. (1) (2) B. (2) (3) C. (2) (4) D. (3) (4)
【答案】B
【解析】 对于(1)中,当时, ,所以不正确;
对于(2)中,根据三角函数的定义,所以当时, 是正确的;
对于(3)中, ,当,解得,
当时, ,函数单调递减,当时, ,函数 单调递增,所以,所以函数的图象与轴只有一个交点,所以函数只有一个零点,所以是正确的;
对于(4)中,当,则,当时, ,所以数列不是等差数列,所以不正确,故选B.
考点二:四种命题
1.四种命题的概念
① 原命题与逆命题
一般地,对于两个命题,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么我们把这样的两个命题叫做互逆命题.其中一个命题叫做原命题,另一个命题叫做原命题的逆命题.也就是说,如果原命题为“若p,则q”,那么它的逆命题为“若q,则p”.
② 否命题
对于两个命题,其中一个命题的条件和结论恰好是另一个命题的条件的否定和结论的否定,我们把这样的两个命题叫做互否命题.其中一个命题叫做原命题,另一个命题叫做原命题的否命题.也就是说,如果原命题为“若p,则q”,那么它的否命题为“若,则”.
③ 逆否命题
对于两个命题,其中一个命题的条件和结论恰好是另一个命题的结论的否定和条件的否定,我们把这样的两个命题叫做互为逆否命题.如果把其中一个命题叫做原命题,那么另一个命题叫做原命题的逆否命题.也就是说,如果原命题为“若p,则q”,那么它的逆否命题为“若,则”.
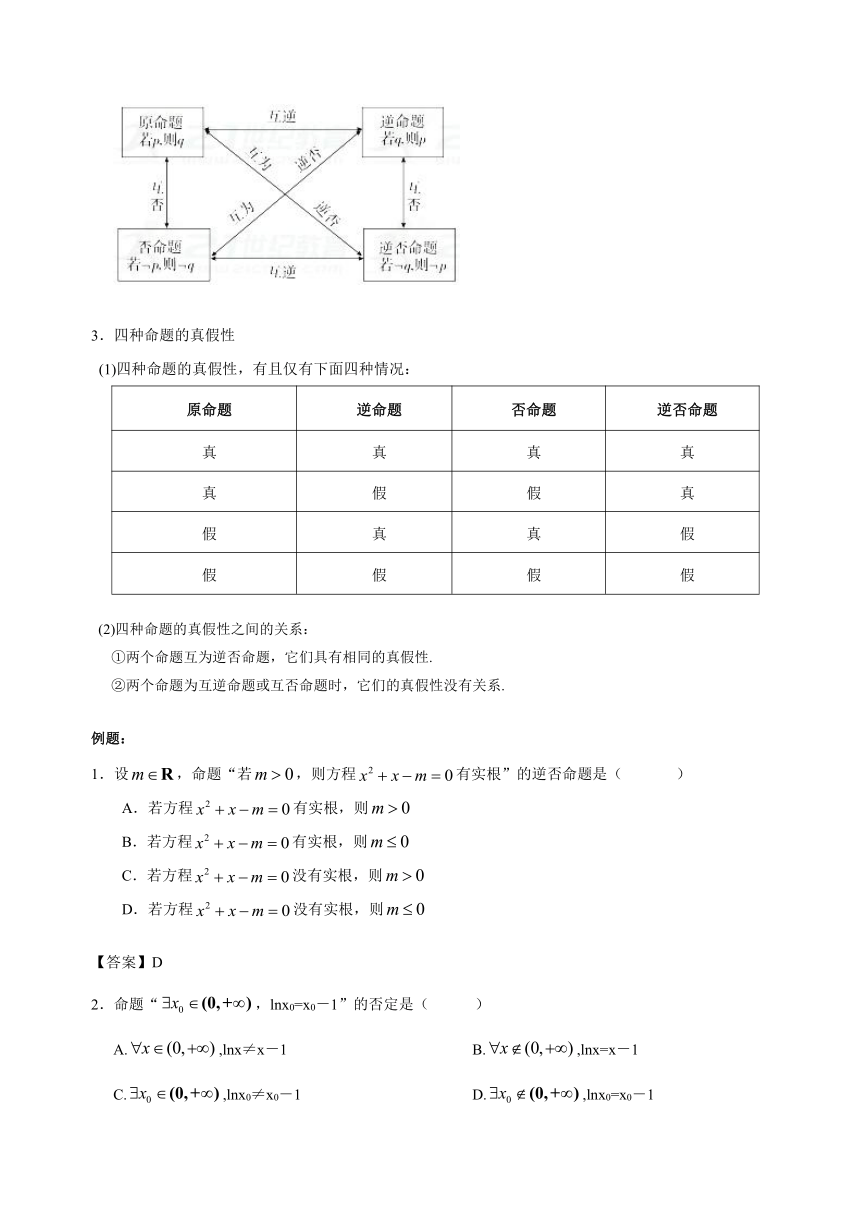
2.四种命题的相互关系
3.四种命题的真假性
(1)四种命题的真假性,有且仅有下面四种情况:
原命题
逆命题
否命题
逆否命题
真
真
真
真
真
假
假
真
假
真
真
假
假
假
假
假
(2)四种命题的真假性之间的关系:
①两个命题互为逆否命题,它们具有相同的真假性.
②两个命题为互逆命题或互否命题时,它们的真假性没有关系.
例题:
1.设,命题“若,则方程有实根”的逆否命题是( )
A.若方程有实根,则
B.若方程有实根,则
C.若方程没有实根,则
D.若方程没有实根,则
【答案】D
2.命题“,lnx0=x0-1”的否定是( )
A.,lnx≠x-1 B.,lnx=x-1
C.,lnx0≠x0-1 D.,lnx0=x0-1
【答案】C
巩固练习
一、选择题
1.命题“若,则中至少有一个大于”的否命题为( )
A. 若中至少有一个大于,则
B. 若,则中至多有一个大于
C. 若,则中至少有一个大于
D. 若,则都不大于
2.命题“若,则”的逆否命题为( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
3.我国古代太极图是一种优美的对称图.如果一个函数的图像能够将圆的面积和周长分成两个相等的部分,我们称这样的函数为圆的“太极函数”.下列命题中错误命题的个数是( )
对于任意一个圆其对应的太极函数不唯一;
如果一个函数是两个圆的太极函数,那么这两个圆为同心圆;
圆的一个太极函数为;
圆的太极函数均是中心对称图形;
奇函数都是太极函数;
偶函数不可能是太极函数.
A. 2 B. 3 C. 4 D. 5
4.下列说法正确的是( )
A. 命题“”的否定是:“”
B. “”是“”的必要不充分条件
C. 命题“若,则”的否命题是:若,则
D. 命题“若,则”的逆否命题为真命题.
5.已知命题p:|x-1|+|x+1|≥3a恒成立,命题q:y=(2a-1)x为减函数,若p且q为真命题,则a的取值范围是( )
A. a B. 0<a<
C. D.
6.已知条件条件且的一个充分不必要条件是,则的取值范围是
A. B. C. D.
二、填空题
7.下列说法中所有正确命题的序号是__________.
①“”是“”成立的充分非必要条件;
②、,则“”是“”的必要非充分条件;
③若一个命题的逆命题为真,则它的否命题一定为真;
④设等比数列的前项和为,则“”是“”成立的充要条件.
三、解答题
8.已知命题: , ;命题: ,使.若“或”为真,“且”为假,求实数的取值范围.
9.已知, .
(1)若为真命题,求实数的取值范围;
(2)若是成立的充分不必要条件,求实数的取值范围.
参考答案与解析
1.D
【解析】“中至少有一个大于”表示“中只有一个大于”或“中两个都大于”,故其否定为“没有一个大于”,所以所给命题的否命题为“若,则都不大于”。选D。
2.B
【解析】由题意得,命题“若,则”的逆否命题为“若,则”。选B。
3.C
故错误;奇函数的图象关于原点对称,其图象可以将任意以原点为圆心的圆面积及周长进行平分,故奇函数可以为太极函数,故正确;如图所示
偶函数可以是太极函数,故错误;则错误的命题有3个,故选C.
4.D
5.C
【解析】命题p:|x-1|+|x+1|≥3a恒成立,由于|x-1|+|x+1|≥2,故有3a≤2,即命题q:
为减函数,可得2a-1∈(0,1),即a∈(,又p且q为真命题,可得a∈
故选C
6.A
【解析】解 得?3?x<1,不等式x2+x
∴该命题的逆否命题为:若q,则p;
∴若?a>a?1,则:不等式(x+a)(x+1?a)<0的解是a?1
若?a
∴a的取值范围是[?1,2].
本题选择A选项.
7.②③④
对于③中,原命题的逆命题与原命题的否命题,互为逆否关系,说以一个命题的逆命题为真,则它的否命题一定为真是正确的;
对于④中,在等比数列中,当时, ,即成立,
当时,则,所以,所以在等比数列中, 是的充要条件,所以是正确的,故选②③④.
8.
【解析】试题分析:先根据分离变量法将不等式恒成立转化为对应函数最值,求得命题为真时实数的取值范围,再根据二次函数图像得不等式有解条件,解得命题为真时实数的取值范围,最后根据“或”为真,“且”为假得与为一真一假,分别解对应不等式组,求并集得结果
试题解析:依题意得: 对成立;
∴;
∵,使
∴不等式的解集非空
∴即或
∵或为真, 且为假;
∴与为一真一假
当真假时, ∴
当假真时, ∴
∴实数的取值范围是
9.:(1)-2≤x≤8.(2)m≥6.
所以当p为真命题时,实数x的取值范围为-2≤x≤8.
(2)解法一:若q为真,可由x2-4x+4-m2≤0(m>0),解得2-m≤x≤2+m(m>0).
若p是q成立的充分不必要条件,则[-2,8]是[2-m,2+m]的真子集,
所以 (两等号不同时成立),得m≥6.
所以实数m的取值范围是m≥6.
解法二:设f(x)=x2-4x+4-m2(m>0),
若p是q成立的充分不必要条件,
∵x2-4x+4-m2≤0在[-2,8]恒成立,
则有 (两等号不同时成立),解得m≥6.
同课章节目录
