破题致胜——期末复习检测高一数学:第二章基本初等函数(I)2.3幂函数
文档属性
| 名称 | 破题致胜——期末复习检测高一数学:第二章基本初等函数(I)2.3幂函数 |  | |
| 格式 | zip | ||
| 文件大小 | 355.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-04 08:35:13 | ||
图片预览

文档简介
复习指导
考点:幂函数及其性质
1.幂函数的概念
一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.
2.幂函数y=x,y=x2,y=x3,,y=x-1的性质.
y=x
y=x2
y=x3
y=x-1
图象
定义
域
R
R
R
[0,+∞)
(-∞,0)(0,+∞)
值域
R
[0,+∞)
R
[0,+∞)
(-∞,0)(0,+∞)
奇偶
性
奇函数
偶函数
奇函数
非奇非偶函数
奇函数
单调
性
在(-∞,+∞)上单调递增
在(-∞,0]
上单调递减,在(0,+∞)上单调递增
在(-∞,+∞)上单调递增
在[0,+∞)
上单调递增
在(-∞,0)上单调递学
在(0,+∞)上单调递减
定点
(1,1),(0,0)
(1,1),(0,0)
(1,1),(0,0)
(1,1),(0,0)
(1,1)
3.幂函数y=xα在第一象限的特征
α的范围
过定点
单调性
α>0[
α>1
(0,0),(1,1)
下凸递增
0<α<1
上凸递增
α<0
(1,1)
递减,且以两坐标轴为渐近线
幂函数的奇偶性
解题指导:求幂函数的定义域时,首先改写成分式或根式形式,再由分式、根式有意义求定义域.
例题:
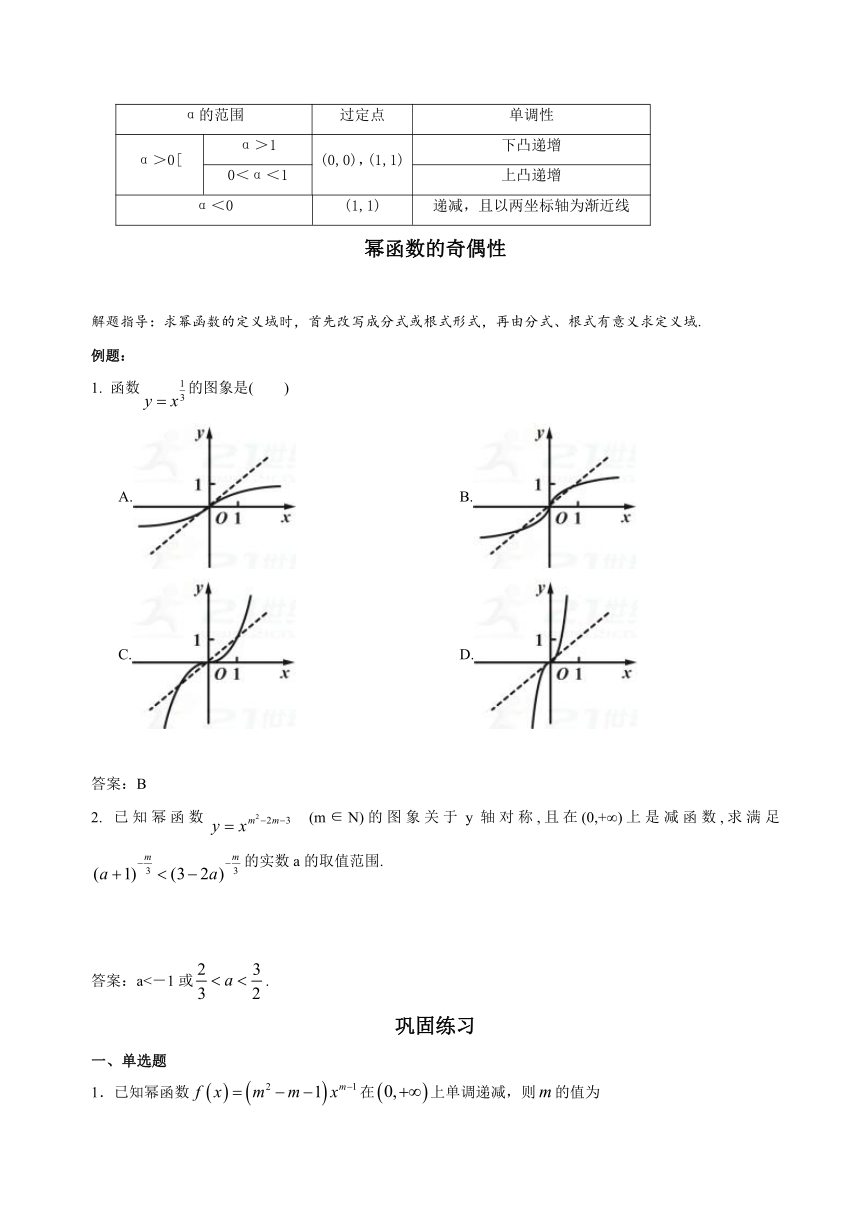
1. 函数的图象是( )
A. B.
C. D.
答案:B
2. 已知幂函数 (m∈N)的图象关于y轴对称,且在(0,+∞)上是减函数,求满足的实数a的取值范围.
答案:a<-1或.
巩固练习
一、单选题
1.已知幂函数在上单调递减,则的值为
A. B. C. 或 D.
2.已知函数是幂函数,则
A. 2 B. C. D. 0
3.若函数为幂函数,且当时, 是增函数,则函数( )
A. B. C. D.
4.已知幂函数的图象过点,则 ( )
A. B. C. D.
5.已知幂函数在上为减函数,则等于
A. 3 B. 4 C. -2 D. -2或3
6.已知幂函数的图像关于原点对称,且在上是减函数,则( )
A. 0 B. 0或2 C. 0 D. 2
二、填空题
7.若幂函数的图象不过原点,则是__________.
8.若幂函数的图象经过点,则__________.
9.已知函数是定义在上的奇函数,当时, ,则__________.
10.已知函数, ,如果成立,则实数的取值范围为__________.
参考答案与解析
1.A
【解析】由函数为幂函数得,即,解得或。当时, ,符合题意。当时, ,不和题意。
综上。选A。
2.D
【解析】∵函数是幂函数
∴,即
∴
故选:D
3.D
当时, ,在是增函数,符合题意。
所以。选D。
4.D
【解析】,则, ,所以,故选D。
5.C
【解析】幂函数在上为减函数,
解得
即
故选
6.B
【解析】幂函数在上是减函数,所以,解得,又,所以,当时, 不是奇函数,所以,故选B.
7.
【解析】幂函数的图象不过原点, ,解得,故答案为.
8.
【解析】由题意有: ,
则: .
9.1
10.
【解析】因为函数, 为奇函数,又恒成立,所以在R上递增,? ,可化为,? 由递增,得 .
