2017-2018上人教版八年级数学下册(广西)期末复习(一)二次根式(含答案)
文档属性
| 名称 | 2017-2018上人教版八年级数学下册(广西)期末复习(一)二次根式(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 216.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-04 00:00:00 | ||
图片预览





文档简介
广西期末复习(一) 二次根式
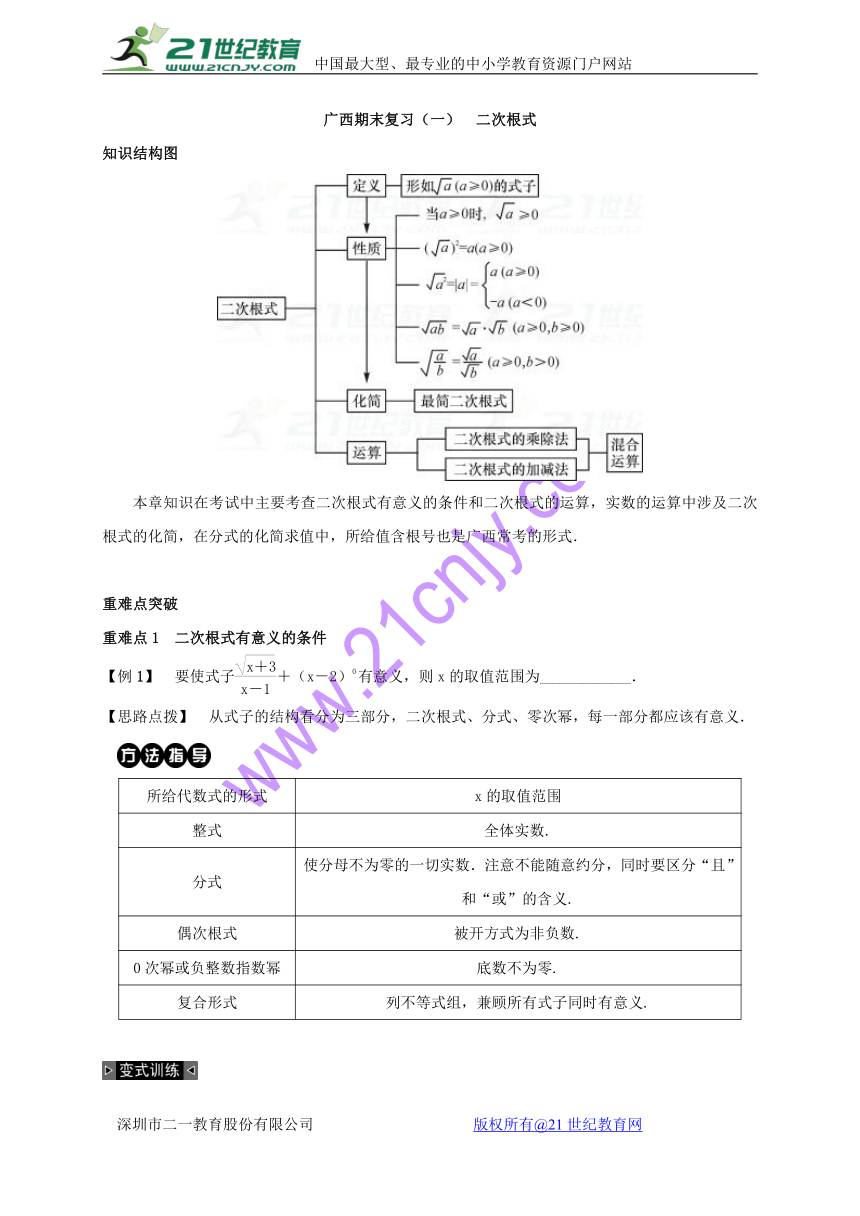
知识结构图
本章知识在考试中主要考查二次根式有意义的条件和二次根式的运算,实数的运算中涉及二次根式的化简,在分式的化简求值中,所给值含根号也是广西常考的形式.21世纪教育网版权所有
重难点突破
重难点1 二次根式有意义的条件
【例1】 要使式子+(x-2)0有意义,则x的取值范围为____________.
【思路点拨】 从式子的结构看分为三部分,二次根式、分式、零次幂,每一部分都应该有意义.
所给代数式的形式
x的取值范围
整式
全体实数.
分式
使分母不为零的一切实数.注意不能随意约分,同时要区分“且”和“或”的含义.
偶次根式
被开方式为非负数.
0次幂或负整数指数幂
底数不为零.
复合形式
列不等式组,兼顾所有式子同时有意义.
1.若有意义,则实数x的取值范围是( )
A.x≥ B.x≥-
C.x> D.x≠
2.若代数式有意义,则实数x的取值范围是( )
A.x≥-1 B.x≥-1且x≠3
C.x>-1 D.x>-1且x≠3
重难点2 二次根式的非负性
【例2】 (2016·南宁)若实数a,b满足|a+2|+=0,则=____________.
这一类问题主要利用非负数的和为0,进而得出每一个非负数的式子为0构造方程求未知数的值,通常利用的非负数有:(1)≥0;(2)x2≥0;(3)≥0.21教育网
3.(2016·泰州)实数a,b满足+4a2+4ab+b2=0,则ba的值为( )
A.2 B. C.-2 D.-
重难点3 二次根式的运算
【例3】 (2017·南宁月考)计算:
(1)(-)-(+); (2)2×÷.
【解答】
二次根式的运算是实数运算中的一种,运算顺序与运算律都遵循有理数的运算顺序与运算律.
4.(2017·玉林期中)计算:4+-.
5.计算:(1-)++()-1.
重难点4 与二次根式有关的化简求值
【例4】 (2016·青海)先化简,再求值:(x-)÷,其中x=2+.
【解答】
将二次根式的运算与分式的化简求值相结合考查,是最常见的考查形式.当未知数的值含根号时,求值时就用到二次根式的运算.21cnjy.com
6.(2017·钦州钦南区月考)先化简,再求值:-,其中x=+1,y=-1.
重难点5 与二次根式有关的规律探究
【例5】 (2016·黄石)观察下列等式:
第1个等式:a1==-1;
第2个等式:a2==-;
第3个等式:a3==2-;
第4个等式:a4==-2.
按上述规律,回答以下问题:
(1)请写出第n个等式:an=__________________;
(2)a1+a2+a3+…+an=________________.
【思路点拨】 (1)观察上面四个式子可得第n个等式;(2)根据所得的规律可得a1+a2+a3+…+an=-1+-+2-+-2+…+-.
规律的探究都遵循从特殊到一般的思维过程,在探究过程中要认真分析等式左右两边“变的量”与“不变的量”.
7.下面是一个按某种规律排列的数阵:
1
第1行
2
第2行
2
3
2
第3行
4
3
2
第4行
…
…
…
…
…
…
…
…
…
根据数阵排列的规律,第n(n是整数,且n≥3)行从左向右数第n-2个数是________________(用含n的代数式表示).
备考集训
一、选择题(每小题4分,共32分)
1.(2017·南宁月考)以下式子中,一定是二次根式的是( )
A. B. C. D.
2.(2017·玉林期中)下列各式成立的是( )
A.=-2 B.=2
C.=±6 D.=±5
3.下列二次根式中,可与进行合并的二次根式为( )
A. B. C. D.
4.(2017·钦州月考)计算:·=( )
A.a B.12a2b
C.a2 D.2a
5.设m=3,n=2,则m,n的大小关系为( )
A.m>n B.m=n
C.m<n D.不能确定
6.已知x+y=3+2,x-y=3-2,则的值为( )
A.4 B.6
C.1 D.3-2
7.若=-a,则a的取值范围是( )
A.-3≤a≤0 B.a≤0
C.a<0 D.a≥-3
8.已知一个等腰三角形的两条边长a,b满足|a-2|+=0,则这个三角形的周长为( )
A.4+5 B.2+5
C.2+10 D.4+5或2+10
二、填空题(每小题3分,共18分)
9.(2017·南宁期末)当x____________时,有意义.
10.(2016·金华)能够说明“=x不成立”的x的值是____________(写出一个即可).
11.(2016·南京)比较大小:-3____________.(填“>”“<”或“=”)
12.若m,n都是无理数,且m+n=2,则m,n的值可以是m=________________,n=________________.(填一组即可)
13.在实数范围内分解因式:4m2-7=________________.
14.当x≤0时,化简|1-x|-的结果是____________.
三、解答题(共50分)
15.(8分)计算:
(1)×÷;
(2)(2017·钦州期末)(2-3)÷.
16.(10分)(2017·玉林期末)已知x=,y=,求+的值.
17.(10分)先化简,再求值:2(a+)(a-)-a(a-6)+6,其中a=-1.
18.(10分)若实数a,b,c满足|a-|+=+.
(1)求a,b,c;
(2)若满足上式的a,b为等腰三角形的两边,求这个等腰三角形的周长.
19.(12分)如图,在8×10的网格内取A,B,C,D四个格点,使AB=BC=2CD=4.P是线段BC上的动点,连接AP,DP.
(1)设BP=a,CP=b,用含字母a,b的代数式分别表示线段AP,DP的长;
(2)设k=AP+DP,k是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
参考答案
广西期末复习(一) 二次根式
【例1】 x≥-3且x≠1,x≠2
【例2】 -
【例3】 (1)原式=2--2-=-3.
(2)原式=2××=.
【例4】 原式=÷=·=·=.当x=2+时,原式===.
【例5】 (1)=- (2)-1
变式训练
1.C 2.B 3.B
4.原式=4+3-2=5.
5.原式=-3+2+3=3.
6.原式=-==.
当x=+1,y=-1时,原式===2.
7.
备考集训
1.A 2.B 3.D 4.D 5.A 6.C 7.A 8.C 9.≥2 10.答案不唯一,如:-1 11.< 12.1+ 1- 13.(2m+)(2m-) 14.1
15.(1)原式=5××=10.
(2)原式=2-3=2-6.
16.∵x+y==5,xy==1,∴+====3.
17.原式=a2+6a.当a=-1时,原式=4-3.
18.(1)由题意,得c-3≥0,3-c≥0,即c=3.∴|a-|+=0.∴a-=0,b-2=0,即a=,b=2.(2)当a是腰长,b是底边长时,等腰三角形的周长为++2=2+2;当b是腰长,a是底边长时,等腰三角形的周长为+2+2=+4.综上,这个等腰三角形的周长为2+2或+4.
19.(1)AP=,DP=.(2)k存在最小值.作点A关于BC的对称点A′,连接A′D,交BC于点P,连接AP,过A′作A′E⊥DC于点E.∴AP=A′P.∴k=AP+DP=A′P+DP====2.
知识结构图
本章知识在考试中主要考查二次根式有意义的条件和二次根式的运算,实数的运算中涉及二次根式的化简,在分式的化简求值中,所给值含根号也是广西常考的形式.21世纪教育网版权所有
重难点突破
重难点1 二次根式有意义的条件
【例1】 要使式子+(x-2)0有意义,则x的取值范围为____________.
【思路点拨】 从式子的结构看分为三部分,二次根式、分式、零次幂,每一部分都应该有意义.
所给代数式的形式
x的取值范围
整式
全体实数.
分式
使分母不为零的一切实数.注意不能随意约分,同时要区分“且”和“或”的含义.
偶次根式
被开方式为非负数.
0次幂或负整数指数幂
底数不为零.
复合形式
列不等式组,兼顾所有式子同时有意义.
1.若有意义,则实数x的取值范围是( )
A.x≥ B.x≥-
C.x> D.x≠
2.若代数式有意义,则实数x的取值范围是( )
A.x≥-1 B.x≥-1且x≠3
C.x>-1 D.x>-1且x≠3
重难点2 二次根式的非负性
【例2】 (2016·南宁)若实数a,b满足|a+2|+=0,则=____________.
这一类问题主要利用非负数的和为0,进而得出每一个非负数的式子为0构造方程求未知数的值,通常利用的非负数有:(1)≥0;(2)x2≥0;(3)≥0.21教育网
3.(2016·泰州)实数a,b满足+4a2+4ab+b2=0,则ba的值为( )
A.2 B. C.-2 D.-
重难点3 二次根式的运算
【例3】 (2017·南宁月考)计算:
(1)(-)-(+); (2)2×÷.
【解答】
二次根式的运算是实数运算中的一种,运算顺序与运算律都遵循有理数的运算顺序与运算律.
4.(2017·玉林期中)计算:4+-.
5.计算:(1-)++()-1.
重难点4 与二次根式有关的化简求值
【例4】 (2016·青海)先化简,再求值:(x-)÷,其中x=2+.
【解答】
将二次根式的运算与分式的化简求值相结合考查,是最常见的考查形式.当未知数的值含根号时,求值时就用到二次根式的运算.21cnjy.com
6.(2017·钦州钦南区月考)先化简,再求值:-,其中x=+1,y=-1.
重难点5 与二次根式有关的规律探究
【例5】 (2016·黄石)观察下列等式:
第1个等式:a1==-1;
第2个等式:a2==-;
第3个等式:a3==2-;
第4个等式:a4==-2.
按上述规律,回答以下问题:
(1)请写出第n个等式:an=__________________;
(2)a1+a2+a3+…+an=________________.
【思路点拨】 (1)观察上面四个式子可得第n个等式;(2)根据所得的规律可得a1+a2+a3+…+an=-1+-+2-+-2+…+-.
规律的探究都遵循从特殊到一般的思维过程,在探究过程中要认真分析等式左右两边“变的量”与“不变的量”.
7.下面是一个按某种规律排列的数阵:
1
第1行
2
第2行
2
3
2
第3行
4
3
2
第4行
…
…
…
…
…
…
…
…
…
根据数阵排列的规律,第n(n是整数,且n≥3)行从左向右数第n-2个数是________________(用含n的代数式表示).
备考集训
一、选择题(每小题4分,共32分)
1.(2017·南宁月考)以下式子中,一定是二次根式的是( )
A. B. C. D.
2.(2017·玉林期中)下列各式成立的是( )
A.=-2 B.=2
C.=±6 D.=±5
3.下列二次根式中,可与进行合并的二次根式为( )
A. B. C. D.
4.(2017·钦州月考)计算:·=( )
A.a B.12a2b
C.a2 D.2a
5.设m=3,n=2,则m,n的大小关系为( )
A.m>n B.m=n
C.m<n D.不能确定
6.已知x+y=3+2,x-y=3-2,则的值为( )
A.4 B.6
C.1 D.3-2
7.若=-a,则a的取值范围是( )
A.-3≤a≤0 B.a≤0
C.a<0 D.a≥-3
8.已知一个等腰三角形的两条边长a,b满足|a-2|+=0,则这个三角形的周长为( )
A.4+5 B.2+5
C.2+10 D.4+5或2+10
二、填空题(每小题3分,共18分)
9.(2017·南宁期末)当x____________时,有意义.
10.(2016·金华)能够说明“=x不成立”的x的值是____________(写出一个即可).
11.(2016·南京)比较大小:-3____________.(填“>”“<”或“=”)
12.若m,n都是无理数,且m+n=2,则m,n的值可以是m=________________,n=________________.(填一组即可)
13.在实数范围内分解因式:4m2-7=________________.
14.当x≤0时,化简|1-x|-的结果是____________.
三、解答题(共50分)
15.(8分)计算:
(1)×÷;
(2)(2017·钦州期末)(2-3)÷.
16.(10分)(2017·玉林期末)已知x=,y=,求+的值.
17.(10分)先化简,再求值:2(a+)(a-)-a(a-6)+6,其中a=-1.
18.(10分)若实数a,b,c满足|a-|+=+.
(1)求a,b,c;
(2)若满足上式的a,b为等腰三角形的两边,求这个等腰三角形的周长.
19.(12分)如图,在8×10的网格内取A,B,C,D四个格点,使AB=BC=2CD=4.P是线段BC上的动点,连接AP,DP.
(1)设BP=a,CP=b,用含字母a,b的代数式分别表示线段AP,DP的长;
(2)设k=AP+DP,k是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
参考答案
广西期末复习(一) 二次根式
【例1】 x≥-3且x≠1,x≠2
【例2】 -
【例3】 (1)原式=2--2-=-3.
(2)原式=2××=.
【例4】 原式=÷=·=·=.当x=2+时,原式===.
【例5】 (1)=- (2)-1
变式训练
1.C 2.B 3.B
4.原式=4+3-2=5.
5.原式=-3+2+3=3.
6.原式=-==.
当x=+1,y=-1时,原式===2.
7.
备考集训
1.A 2.B 3.D 4.D 5.A 6.C 7.A 8.C 9.≥2 10.答案不唯一,如:-1 11.< 12.1+ 1- 13.(2m+)(2m-) 14.1
15.(1)原式=5××=10.
(2)原式=2-3=2-6.
16.∵x+y==5,xy==1,∴+====3.
17.原式=a2+6a.当a=-1时,原式=4-3.
18.(1)由题意,得c-3≥0,3-c≥0,即c=3.∴|a-|+=0.∴a-=0,b-2=0,即a=,b=2.(2)当a是腰长,b是底边长时,等腰三角形的周长为++2=2+2;当b是腰长,a是底边长时,等腰三角形的周长为+2+2=+4.综上,这个等腰三角形的周长为2+2或+4.
19.(1)AP=,DP=.(2)k存在最小值.作点A关于BC的对称点A′,连接A′D,交BC于点P,连接AP,过A′作A′E⊥DC于点E.∴AP=A′P.∴k=AP+DP=A′P+DP====2.
