2018年春人教版八年级数学下册(广西) 期末复习学案(四) 一次函数(含答案)
文档属性
| 名称 | 2018年春人教版八年级数学下册(广西) 期末复习学案(四) 一次函数(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 262.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-04 00:00:00 | ||
图片预览




文档简介
广西期末复习(四) 一次函数
知识结构图
本章知识在考试中主要考查一次函数的图象与性质,确定一次函数解析式及一次函数的实际应用,其中运用一次函数选择方案是难点,复习时应强化.
重难点突破
重难点1 函数图象
【例1】 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒,在跑步过程中,甲、乙两人之间的距离y(m)与乙出发的时间t(s)之间的函数关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )
A.①②③
B.仅有①②
C.仅有①③
D.仅有②③
【思路点拨】 通过对函数图象的分析及行程问题的数量关系可以求出甲、乙的速度;b的值就是乙到达终点时与甲之间的距离,a表示乙追上甲的时间,c表示乙出发后到甲到达终点的时间.根据行程问题之间的数量关系就可以得出结论.甲的速度为:8÷2=4(m/s);乙的速度为:500÷100=5(m/s);b=5×100-4×(100+2)=92(m);5a-4×(a+2)=0,解得a=8,c=100+92÷4=123.
解决此类题的关键是弄清函数图象的意义,解题时要注重生活实际,通过看图进行思考和分析,活用数学知识,学会把实际问题转化为数学问题.
1.甲、乙两人以相同路线前往距离单位10 km的培训中心参加学习.图中l甲,l乙分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8 km后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
重难点2 一次函数的图象与性质
【例2】 (2016·郴州)当b<0时,一次函数y=x+b的图象大致是( )
一次函数y=kx+b的图象和性质与解析式中的k,b有关,如表:
k>0
k<0
图象
经过象限
一、二、三
一、三
一、三、四
一、二、四
二、四
二、三、四
增减性
y随x的增大而增大
y随x的增大而减小
2.若一次函数y=kx+b的函数值y随x的增大而减小,且图象与y轴的正半轴相交,那么对k和b的符号判断正确的是( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
3.已知直线y=kx+b,若k+b=-5,kb=6,那么该直线不经过第____________象限.
重难点3 确定一次函数解析式
【例3】 已知:一次函数y=kx+b的图象经过(0,2),(1,3)两点.
(1)求k,b的值;
(2)若一次函数y=kx+b的图象与x轴的交点为A(a,0),求a的值.
【思路点拨】 (1)用待定系数法可求k,b;(2)把A(a,0)代入求出的解析式即可求出a值.
【解答】
求一次函数的解析式都是把已知点的坐标代入解析式,运用待定系数法求出k,b;当求与坐标轴的交点坐标时,根据坐标轴上点的坐标特征代入解析式求出符合题意的解.
4.已知y是x的一次函数,且其图象过点(3,1)和(-2,-4).
(1)求此一次函数的解析式;
(2)求一次函数的图象与两坐标轴的交点坐标.
重难点4 一次函数与方程、不等式
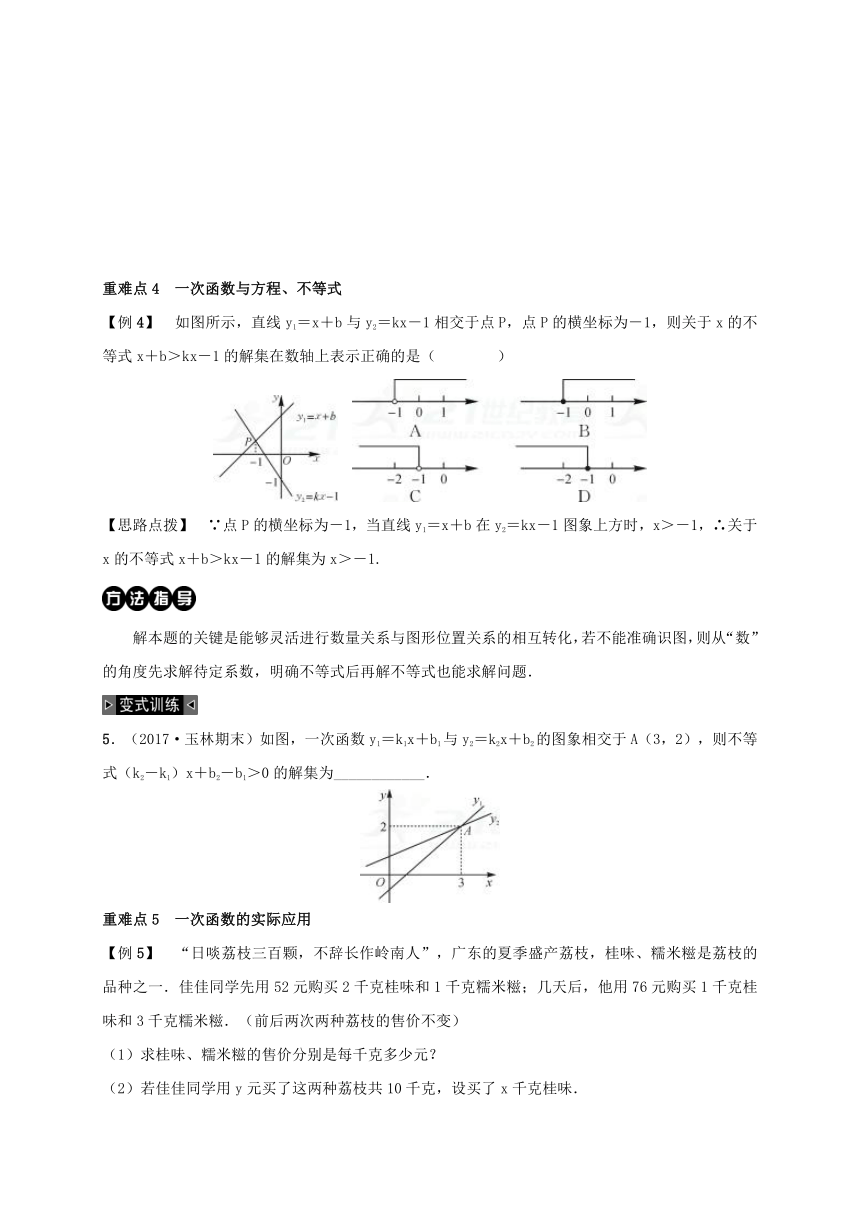
【例4】 如图所示,直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集在数轴上表示正确的是( )
【思路点拨】 ∵点P的横坐标为-1,当直线y1=x+b在y2=kx-1图象上方时,x>-1,∴关于x的不等式x+b>kx-1的解集为x>-1.
解本题的关键是能够灵活进行数量关系与图形位置关系的相互转化,若不能准确识图,则从“数”的角度先求解待定系数,明确不等式后再解不等式也能求解问题.
5.(2017·玉林期末)如图,一次函数y1=k1x+b1与y2=k2x+b2的图象相交于A(3,2),则不等式(k2-k1)x+b2-b1>0的解集为____________.
重难点5 一次函数的实际应用
【例5】 “日啖荔枝三百颗,不辞长作岭南人”,广东的夏季盛产荔枝,桂味、糯米糍是荔枝的品种之一.佳佳同学先用52元购买2千克桂味和1千克糯米糍;几天后,他用76元购买1千克桂味和3千克糯米糍.(前后两次两种荔枝的售价不变)
(1)求桂味、糯米糍的售价分别是每千克多少元?
(2)若佳佳同学用y元买了这两种荔枝共10千克,设买了x千克桂味.
①写出y与x的函数关系式;
②若要求糯米糍的重量不少于桂味重量的3倍,请帮佳佳同学设计一个购买方案,使所需的费用最少,并求出最少费用.
【解答】
此题主要考查了一次函数的应用,关键是求函数的关系式,以及求自变量时把函数值正确代入相对应的函数.
6.随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水,某市对居民用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示.图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元),请根据图象信息,回答下列问题:
(1)该市人均月生活用水的收费标准是:不超过5吨,每吨按____________元收取;超过5吨的部分,每吨按____________元收取;
(2)请写出y与x的函数关系式;
(3)若某个家庭有5人,五月份的生活用水费共76元,则该家庭这个月用了多少吨生活用水?
备考集训
一、选择题(每小题4分,共32分)
1.当x=3时,函数y=-2x+1的值是( )
A.-5 B.3 C.7 D.5
2.函数y=+的自变量x的取值范围是( )
A.x≤3 B.x≠4
C.x≥3且x≠4 D.x≤3或x≠4
3.若正比例函数的图象经过点(-1,2),则这个图象必经过点( )
A.(1,2) B.(-1,-2)
C.(2,-1) D.(1,-2)
4.对于一次函数y=kx+k-1(k≠0),下列叙述正确的是( )
A.当0<k<1时,函数图象经过第一、二、三象限
B.当k>0时,y随x的增大而减小
C.当k<1时,函数图象一定交于y轴的负半轴
D.函数图象一定经过点(-1,-2)
5.正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )
6.如图,直线y=kx+b与y轴交于点(0,3),与x轴交于点(a,0),当a满足-3≤a<0时,k的取值范围是( )
A.-1≤k<0 B.1≤k≤3
C.k≥1 D.k≥3
7.惠农种子公司以一定价格销售“丰收一号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间函数关系如图所示.下列四种说法:①一次购买30千克种子时,付款金额为1 000元;②一次购买种子数量不超过10千克时,销售价格为50元/千克;③一次购买10千克以上种子时,超过10千克的那部分种子的价格打五折;④一次购买40千克种子比分两次购买且每次购买20千克种子少花200元钱,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.已知四条直线y=kx-3,y=-1,y=3和x=1所围成的四边形的面积是12,则k的值为( )
A.1或-2 B.2或-1
C.3 D.4
二、填空题(每小题3分,共18分)
9.在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1),P2(x2,y2)两点.若x1<x2,则y1____________y2.(填“>”“<”或“=”)
10.(2017·玉林期末)一条直线与已知直线y=-3x+1平行,这条直线可以为________________.
11.如果直线y=2x+m不经过第二象限,那么实数m的取值范围是____________.
12.若一次函数y1=kx-b的图象经过第一、三、四象限,则一次函数y2=bx+k的图象经过第____________象限.
13.将直线y=2x+1平移后经过点(2,1),则平移后的直线解析式为____________.
14.一次函数y=kx+b,当3≤x≤4时,3≤y≤6,则的值是____________.
三、解答题(共50分)
15.(12分)已知y+2与x成正比例,且当x=-2时,y=0.
(1)求y与x之间的函数关系式;
(2)画出函数的图象;
(3)观察图象,当x取何值时,y≥0;
(4)若点(m,6)在该函数的图象上,求m的值.
16.(12分)如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的解析式;
(2)若直线AB上一点C在第一象限且点C的坐标为(2,2),求△BOC的面积.
17.(12分)某游泳池普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费;
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常销售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一平面直角坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A,B,C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
18.(14分)梧州市特产批发市场有龟苓膏粉批发,其中A品牌的批发价是每包20元,B品牌的批发价是每包25元,小王需购买A,B两种品牌的龟苓膏粉共1 000包.
(1)若小王按需购买A,B两种品牌龟苓膏粉共用22 000元,则各购买多少包?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1 000包龟苓膏粉,共用了y元,设A品牌买了x包,请求出y与x之间的函数关系式;
(3)在(2)中,小王共用了20 000元,他计划在网店包邮销售这批龟苓膏粉,每包龟苓膏粉小王需支付邮费8元.若每包销售价格A品牌比B品牌少5元,请你帮他计算,A品牌的龟苓膏粉每包定价不低于多少元时才不亏本(运算结果取整数).
广西期末复习(四) 一次函数
【例1】 A
【例2】 B
【例3】 (1)由题意,得解得(2)由(1)得y=x+2,∴当y=0时,x=-2,即a=-2.
【例4】 A
【例5】 (1)设桂味的售价是每千克m元,糯米糍的售价是每千克n元.根据题意,得解得答:桂味的售价是每千克16元,糯米糍的售价是每千克20元.(2)①设买了x千克桂味,则买了(10-x)千克糯米糍,根据题意,得y=16x+20(10-x)=-4x+200(0<x<10).②∵糯米糍的重量不少于桂味重量的3倍,∴10-x≥3x.∴x≤.∵y=-4x+200中,k=-4<0,∴y值随x值的增大而减小.∴当x=时,y取最小值,最小值为190.答:当购买桂味千克、糯米糍千克时,所需的费用最少,最少费用为190元.
变式训练
1.B 2.C 3.一
4.(1)设一次函数解析式为y=kx+b,由题意,得解得∴该一次函数的解析式为y=x-2.(2)当x=0时,y=-2,∴一次函数的图象与y轴交点坐标为(0,-2).当y=0时,x-2=0,解得x=2.∴一次函数的图象与x轴交点坐标为(2,0).
5.x<3
7.(1)1.6 2.4 (2)当0≤x≤5时,设y=kx,将(5,8)代入,得8=5k,即k=.∴y=x.当x>5时,设y=kx+b,将(5,8),(10,20)代入,得解得∴y=x-4.综上所述,y=(3)由题意,得x-4=.解得x=8.∴5×8=40(吨).答:该家庭这个月共用了40吨生活用水.
备考集训
1.A 2.A 3.D 4.C 5.B 6.C 7.C 8.A 9.< 10.y=-3x+5(答案不唯一) 11.m≤0 12.一、二、三 13.y=2x-3 14.-2或-5
15.(1)y=-x-2.(2)图象略.(3)当x≤-2时,y≥0.(4)m=-8.
16.(1)设直线AB的解析式为y=kx+b(k≠0).将A(1,0),B(0,-2)代入解析式,得解得∴直线AB的解析式为y=2x-2.(2)S△BOC=×2×2=2.
17.(1)选择银卡消费:y=10x+150;选择普通票消费:y=20x.(2)对于y=10x+150,令x=0,则y=150.∴A(0,150).联立解得∴B(15,300).令y=600,则10x+150=600,解得x=45,∴C(45,600).(3)根据图象可知:当0≤x<15时,选择普通票消费合算;当x=15时,选择银卡和普通票消费一样;当15<x<45时,选择银卡消费合算;当x=45时,选择金卡和银卡消费一样;当x>45时,选择金卡消费合算.
18.(1)设小王购买A,B两种品牌龟苓膏粉分别为x包,y包,由题意,得解得答:小王购买A,B两种品牌龟苓膏粉分别为600包,400包.(2)由题意,得y=500+0.8×[20x+25(1 000-x)]=500+0.8×(25 000-5x)=-4x+20 500.∴y与x之间的函数关系式是:y=-4x+20 500.(3)由(2)可得20 000=-4x+20 500,解得x=125.∴小王购买A,B两种品牌龟苓膏粉分别为125包,875包.设A种品牌龟苓膏粉的售价为z元,则B种品牌龟苓膏粉的售价为(z+5)元,∴125z+875(z+5)≥20 000+8×1 000.解得z≥23.625.答:A品牌的龟苓膏粉每包定价不低于24元时才不亏本.
知识结构图
本章知识在考试中主要考查一次函数的图象与性质,确定一次函数解析式及一次函数的实际应用,其中运用一次函数选择方案是难点,复习时应强化.
重难点突破
重难点1 函数图象
【例1】 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒,在跑步过程中,甲、乙两人之间的距离y(m)与乙出发的时间t(s)之间的函数关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )
A.①②③
B.仅有①②
C.仅有①③
D.仅有②③
【思路点拨】 通过对函数图象的分析及行程问题的数量关系可以求出甲、乙的速度;b的值就是乙到达终点时与甲之间的距离,a表示乙追上甲的时间,c表示乙出发后到甲到达终点的时间.根据行程问题之间的数量关系就可以得出结论.甲的速度为:8÷2=4(m/s);乙的速度为:500÷100=5(m/s);b=5×100-4×(100+2)=92(m);5a-4×(a+2)=0,解得a=8,c=100+92÷4=123.
解决此类题的关键是弄清函数图象的意义,解题时要注重生活实际,通过看图进行思考和分析,活用数学知识,学会把实际问题转化为数学问题.
1.甲、乙两人以相同路线前往距离单位10 km的培训中心参加学习.图中l甲,l乙分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8 km后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
重难点2 一次函数的图象与性质
【例2】 (2016·郴州)当b<0时,一次函数y=x+b的图象大致是( )
一次函数y=kx+b的图象和性质与解析式中的k,b有关,如表:
k>0
k<0
图象
经过象限
一、二、三
一、三
一、三、四
一、二、四
二、四
二、三、四
增减性
y随x的增大而增大
y随x的增大而减小
2.若一次函数y=kx+b的函数值y随x的增大而减小,且图象与y轴的正半轴相交,那么对k和b的符号判断正确的是( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
3.已知直线y=kx+b,若k+b=-5,kb=6,那么该直线不经过第____________象限.
重难点3 确定一次函数解析式
【例3】 已知:一次函数y=kx+b的图象经过(0,2),(1,3)两点.
(1)求k,b的值;
(2)若一次函数y=kx+b的图象与x轴的交点为A(a,0),求a的值.
【思路点拨】 (1)用待定系数法可求k,b;(2)把A(a,0)代入求出的解析式即可求出a值.
【解答】
求一次函数的解析式都是把已知点的坐标代入解析式,运用待定系数法求出k,b;当求与坐标轴的交点坐标时,根据坐标轴上点的坐标特征代入解析式求出符合题意的解.
4.已知y是x的一次函数,且其图象过点(3,1)和(-2,-4).
(1)求此一次函数的解析式;
(2)求一次函数的图象与两坐标轴的交点坐标.
重难点4 一次函数与方程、不等式
【例4】 如图所示,直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集在数轴上表示正确的是( )
【思路点拨】 ∵点P的横坐标为-1,当直线y1=x+b在y2=kx-1图象上方时,x>-1,∴关于x的不等式x+b>kx-1的解集为x>-1.
解本题的关键是能够灵活进行数量关系与图形位置关系的相互转化,若不能准确识图,则从“数”的角度先求解待定系数,明确不等式后再解不等式也能求解问题.
5.(2017·玉林期末)如图,一次函数y1=k1x+b1与y2=k2x+b2的图象相交于A(3,2),则不等式(k2-k1)x+b2-b1>0的解集为____________.
重难点5 一次函数的实际应用
【例5】 “日啖荔枝三百颗,不辞长作岭南人”,广东的夏季盛产荔枝,桂味、糯米糍是荔枝的品种之一.佳佳同学先用52元购买2千克桂味和1千克糯米糍;几天后,他用76元购买1千克桂味和3千克糯米糍.(前后两次两种荔枝的售价不变)
(1)求桂味、糯米糍的售价分别是每千克多少元?
(2)若佳佳同学用y元买了这两种荔枝共10千克,设买了x千克桂味.
①写出y与x的函数关系式;
②若要求糯米糍的重量不少于桂味重量的3倍,请帮佳佳同学设计一个购买方案,使所需的费用最少,并求出最少费用.
【解答】
此题主要考查了一次函数的应用,关键是求函数的关系式,以及求自变量时把函数值正确代入相对应的函数.
6.随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水,某市对居民用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示.图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元),请根据图象信息,回答下列问题:
(1)该市人均月生活用水的收费标准是:不超过5吨,每吨按____________元收取;超过5吨的部分,每吨按____________元收取;
(2)请写出y与x的函数关系式;
(3)若某个家庭有5人,五月份的生活用水费共76元,则该家庭这个月用了多少吨生活用水?
备考集训
一、选择题(每小题4分,共32分)
1.当x=3时,函数y=-2x+1的值是( )
A.-5 B.3 C.7 D.5
2.函数y=+的自变量x的取值范围是( )
A.x≤3 B.x≠4
C.x≥3且x≠4 D.x≤3或x≠4
3.若正比例函数的图象经过点(-1,2),则这个图象必经过点( )
A.(1,2) B.(-1,-2)
C.(2,-1) D.(1,-2)
4.对于一次函数y=kx+k-1(k≠0),下列叙述正确的是( )
A.当0<k<1时,函数图象经过第一、二、三象限
B.当k>0时,y随x的增大而减小
C.当k<1时,函数图象一定交于y轴的负半轴
D.函数图象一定经过点(-1,-2)
5.正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )
6.如图,直线y=kx+b与y轴交于点(0,3),与x轴交于点(a,0),当a满足-3≤a<0时,k的取值范围是( )
A.-1≤k<0 B.1≤k≤3
C.k≥1 D.k≥3
7.惠农种子公司以一定价格销售“丰收一号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间函数关系如图所示.下列四种说法:①一次购买30千克种子时,付款金额为1 000元;②一次购买种子数量不超过10千克时,销售价格为50元/千克;③一次购买10千克以上种子时,超过10千克的那部分种子的价格打五折;④一次购买40千克种子比分两次购买且每次购买20千克种子少花200元钱,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.已知四条直线y=kx-3,y=-1,y=3和x=1所围成的四边形的面积是12,则k的值为( )
A.1或-2 B.2或-1
C.3 D.4
二、填空题(每小题3分,共18分)
9.在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1),P2(x2,y2)两点.若x1<x2,则y1____________y2.(填“>”“<”或“=”)
10.(2017·玉林期末)一条直线与已知直线y=-3x+1平行,这条直线可以为________________.
11.如果直线y=2x+m不经过第二象限,那么实数m的取值范围是____________.
12.若一次函数y1=kx-b的图象经过第一、三、四象限,则一次函数y2=bx+k的图象经过第____________象限.
13.将直线y=2x+1平移后经过点(2,1),则平移后的直线解析式为____________.
14.一次函数y=kx+b,当3≤x≤4时,3≤y≤6,则的值是____________.
三、解答题(共50分)
15.(12分)已知y+2与x成正比例,且当x=-2时,y=0.
(1)求y与x之间的函数关系式;
(2)画出函数的图象;
(3)观察图象,当x取何值时,y≥0;
(4)若点(m,6)在该函数的图象上,求m的值.
16.(12分)如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的解析式;
(2)若直线AB上一点C在第一象限且点C的坐标为(2,2),求△BOC的面积.
17.(12分)某游泳池普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费;
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常销售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一平面直角坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A,B,C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
18.(14分)梧州市特产批发市场有龟苓膏粉批发,其中A品牌的批发价是每包20元,B品牌的批发价是每包25元,小王需购买A,B两种品牌的龟苓膏粉共1 000包.
(1)若小王按需购买A,B两种品牌龟苓膏粉共用22 000元,则各购买多少包?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1 000包龟苓膏粉,共用了y元,设A品牌买了x包,请求出y与x之间的函数关系式;
(3)在(2)中,小王共用了20 000元,他计划在网店包邮销售这批龟苓膏粉,每包龟苓膏粉小王需支付邮费8元.若每包销售价格A品牌比B品牌少5元,请你帮他计算,A品牌的龟苓膏粉每包定价不低于多少元时才不亏本(运算结果取整数).
广西期末复习(四) 一次函数
【例1】 A
【例2】 B
【例3】 (1)由题意,得解得(2)由(1)得y=x+2,∴当y=0时,x=-2,即a=-2.
【例4】 A
【例5】 (1)设桂味的售价是每千克m元,糯米糍的售价是每千克n元.根据题意,得解得答:桂味的售价是每千克16元,糯米糍的售价是每千克20元.(2)①设买了x千克桂味,则买了(10-x)千克糯米糍,根据题意,得y=16x+20(10-x)=-4x+200(0<x<10).②∵糯米糍的重量不少于桂味重量的3倍,∴10-x≥3x.∴x≤.∵y=-4x+200中,k=-4<0,∴y值随x值的增大而减小.∴当x=时,y取最小值,最小值为190.答:当购买桂味千克、糯米糍千克时,所需的费用最少,最少费用为190元.
变式训练
1.B 2.C 3.一
4.(1)设一次函数解析式为y=kx+b,由题意,得解得∴该一次函数的解析式为y=x-2.(2)当x=0时,y=-2,∴一次函数的图象与y轴交点坐标为(0,-2).当y=0时,x-2=0,解得x=2.∴一次函数的图象与x轴交点坐标为(2,0).
5.x<3
7.(1)1.6 2.4 (2)当0≤x≤5时,设y=kx,将(5,8)代入,得8=5k,即k=.∴y=x.当x>5时,设y=kx+b,将(5,8),(10,20)代入,得解得∴y=x-4.综上所述,y=(3)由题意,得x-4=.解得x=8.∴5×8=40(吨).答:该家庭这个月共用了40吨生活用水.
备考集训
1.A 2.A 3.D 4.C 5.B 6.C 7.C 8.A 9.< 10.y=-3x+5(答案不唯一) 11.m≤0 12.一、二、三 13.y=2x-3 14.-2或-5
15.(1)y=-x-2.(2)图象略.(3)当x≤-2时,y≥0.(4)m=-8.
16.(1)设直线AB的解析式为y=kx+b(k≠0).将A(1,0),B(0,-2)代入解析式,得解得∴直线AB的解析式为y=2x-2.(2)S△BOC=×2×2=2.
17.(1)选择银卡消费:y=10x+150;选择普通票消费:y=20x.(2)对于y=10x+150,令x=0,则y=150.∴A(0,150).联立解得∴B(15,300).令y=600,则10x+150=600,解得x=45,∴C(45,600).(3)根据图象可知:当0≤x<15时,选择普通票消费合算;当x=15时,选择银卡和普通票消费一样;当15<x<45时,选择银卡消费合算;当x=45时,选择金卡和银卡消费一样;当x>45时,选择金卡消费合算.
18.(1)设小王购买A,B两种品牌龟苓膏粉分别为x包,y包,由题意,得解得答:小王购买A,B两种品牌龟苓膏粉分别为600包,400包.(2)由题意,得y=500+0.8×[20x+25(1 000-x)]=500+0.8×(25 000-5x)=-4x+20 500.∴y与x之间的函数关系式是:y=-4x+20 500.(3)由(2)可得20 000=-4x+20 500,解得x=125.∴小王购买A,B两种品牌龟苓膏粉分别为125包,875包.设A种品牌龟苓膏粉的售价为z元,则B种品牌龟苓膏粉的售价为(z+5)元,∴125z+875(z+5)≥20 000+8×1 000.解得z≥23.625.答:A品牌的龟苓膏粉每包定价不低于24元时才不亏本.
