21.2.4 一元二次方程根与系数的关系学案(附答案)
文档属性
| 名称 | 21.2.4 一元二次方程根与系数的关系学案(附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 856.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-06 00:00:00 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
21.2.4 一元二次方程的根与系数的关系
知识梳理
1.一元二次方程根与系数的关系(韦达定理):设一元二次方程的两根是x1和x2,则 .21世纪教育网版权所有
2.当一元二次方程的两根是x1和x2时:
(1)若,则方程有 根;
(2)若,则方程有 个正根;
(3)若,则方程有 个负根.
重点突破
知识点 一元二次方程根与系数的关系
1.若x1、x2是一元二次方程x2+10x+16的两个根,则x1+x2的值是( )
A.-10 B.10 C.-16 D.16
【解析】本题主要考查利用根与系数的关系求两根之间关系的代数式的值。根据一元二次方程根与系数的关系得x1+x2=21cnjy.com
【答案】A
【点评】本题考查了根与系数的关系。
2.方程ax2+bx﹣c=0(a>0、b>0、c>0)的两个根的符号为( )
A.同号 B.异号 C.两根都为正 D.不能确定
【解析】本题主要考查利用根与系数的关系求方程中待定字母的值。首先由△=b2+4ac>0,可知方程有两个不等的实数根,再由x1x2=<0可知两根异号.www.21-cn-jy.com
【答案】B
3. 设x1、x2是一元二次方程x2﹣5x﹣1=0的两实数根,则2x1x2的值为________.
【解析】本题主要考查根与系数的关系知识的巧妙运用。首先根据根与系数的关系求出,再求出的值。解:∵x1、x2是一元二次方程x2﹣5x﹣1=0的两实数根,
∴x1+x2=5,x1x2=﹣1,∴2x1x2=﹣2,
【答案】-2.
基础过关
1.已知、是方程的两个实数根,那么下列结论正确的是( )
A.+=-1 B.+=-3 C.+=1 D. +=3
2.已知方程3x2-4x-4=0的两个实数根分别为x1,x2.则x1+x2=( )
A.-3 B. 3 C. D.
3.已知x1,x2是一元二次方程x2-4x+1=0的两个实数根,则x1x2等于( )
A.-4 B.-1 C.1 D.4
4.已知关于x的一元二次方程ax2+bx+c=0(a≠0)的两根互为相反数,则( )
A.b>0 B.b=0 C.b<0 D.c=0
5.已知关于x的一元二次方程x2-(m-1)x-(2m-2)=0的两根之和等于两根之积,则m的值为( )21·cn·jy·com
A.1 B.-1 C.2 D.-2
6.已知一元二次方程x2-x+2=0,则下列说法正确的是( )
A.两根之和为1 B.两根之积为2 C.两根的平方和为-3 D.没有实数根
7.已知实数x1,x2满足x1+x2=7,x1x2=12,则以x1,x2为根的一元二次方程是( )
A.x2﹣7x+12=0 B.x2+7x+12=0 C.x2+7x﹣12=0 D.x2﹣7x﹣12=0
8. 一元二次方程x2+px=2的两根为x1,x2,且x1=﹣2x2,则p的值为( )
A.2 B.1 C.1或﹣1 D.﹣1
9.已知一元二次方程2x2-5x+1=0的两根为m、n,则m2+n2= ___ _.
10.关于x的一元二次方程 ( http: / / www.21cnjy.com )的两个实数根分别为1和2,则 ( http: / / www.21cnjy.com ) , ( http: / / www.21cnjy.com ) .
11.已知 ( http: / / www.21cnjy.com )、 ( http: / / www.21cnjy.com )是方程 ( http: / / www.21cnjy.com )的两实数根,则 ( http: / / www.21cnjy.com )的值是 .
12.已知方程x2+mx+3=0的一个根是1,则它的另一个根是 ,m的值是 .
13.关于的一元二次方程=0的两实数根之积为负,则实数的取值范围是________.
14.已知关于x的一元二次方程有两个不相等的实数根、.
(1)求m的值;
(2)当时,求另一个根的值.
能力拓展
1.已知x1,x2是关于x的方程x2+ax-2b=0的两实数根,且x1+x2=-2,x1·x2=1,则ba的值是( )2·1·c·n·j·y
A. B.- C.4 D.-1
2.关于x的一元二次方程:x2—4x—m2=0有两个实数根x1,x2,则( )
A. B. C.4 D.-4
3.已知一元二次方程的两根分别是2和-3,则这个一元二次方程是( )
A.x2-6x+8=0 B.x2+2x-3=0 C.x2-x-6=0 D.x2+x-6=0
4.有两个一元二次方程:M:ax2+bx+c=0,N:cx2+bx+a=0,其中a·c≠0,a≠c,以下四个结论中,错误的是 ( )
A. 如果方程M有两个相等的实数根,那么方程N也有两个相等的实数根
B. 如果方程M有两根符号相同,那么方程N的两根符号也相同
C. 如果5是方程M的一个根,那么15是方程N的一个根
D. 如果方程M和方程N有一个相同的根,那么这个根必是x=1
5.一若关于x的一元二次方程x2-4x+k-3=0的两个实数根为x1,x2,且满足x1=3x2,试求出方程的两个实数根及k的值.2-1-c-n-j-y
6.关于的一元二次方程有两个不等实根、.
(1)求实数的取值范围;
(2)若方程两实根、满足,求的值.
7.已知关于x的一元二次方程x2-6x+(2m+1)=0有实数根.
①求m的取值范围;
②如果方程的两个实数根为x1,x2,且2x1x2+x1+x2≥20,求m的取值范围.
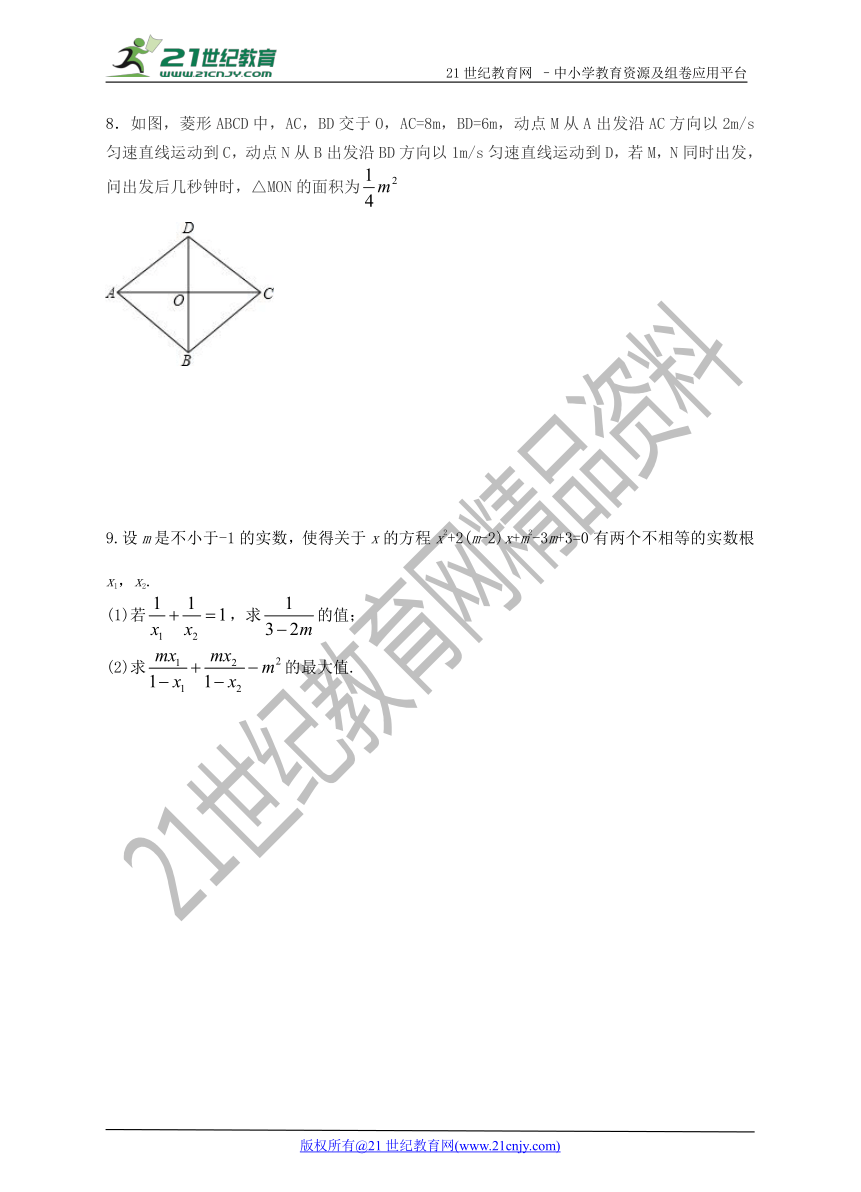
8.如图,菱形ABCD中,AC,BD交于O,AC=8m,BD=6m,动点M从A出发沿AC方向以2m/s匀速直线运动到C,动点N从B出发沿BD方向以1m/s匀速直线运动到D,若M,N同时出发,问出发后几秒钟时,△MON的面积为
【来源:21·世纪·教育·网】
9.设m是不小于-1的实数,使得关于x的 ( http: / / www.21cnjy.com )方程x2+2(m-2)x+m2-3m+3=0有两个不相等的实数根x1,x2.www.21-cn-jy.com21·世纪*教育网
(1)若,求的值;
(2)求的最大值.
参考答案
知识梳理
1..
2.一正一负,2,2
基础过关
1.B
2.D
3.C
4.B
5.A
6.D
7.A
8.C
9.
10.-3,2
11.10
12.3,-4
13.
14. 解:(1)∵一元二次方程有两个不相等的实数根,
∴,∴,∴.
(2)根据一元二次方程根与系数的关系,得,,∴.
能力拓展
1.A
2.D
3.D
4.D
5.解:由根与系数的关系,得 ( http: / / www.21cnjy.com )
又∵x1=3x2,③,
联立①、③,解方程组,得 ( http: / / www.21cnjy.com )
∴k=x1x2+3=3×1+3=6.
答:方程两根为x1=3,x2=1;k=6.
6.解:(1)∵原方程有两个不相等的实数根,
∴, 解得: .
(2)由根与系数的关系,得, .
∵,
∴,
解得:或,
又∵,
∴.
7.解:①根据题意得b2-4ac=(-6)2-4(2m+1)≥0,解得m≤4;
②根据题意得x1+x2=6,x1x2=2m ( http: / / www.21cnjy.com )+1,而2x1x2+x1+x2≥20,所以2(2m+1)+6≥20,解得m≥3,而m≤4,所以m的取值范围为3≤m≤421教育网
8.解:设解:设出发后x秒时,
(1)当x<2时,点M在线段AO上,点N在线段BO上.(4-2x)(3-x)=;
解得x1=,x2=
∵x<2,
∴;
(2)当2<x<3时,点M在线段OC上,点N在线段BO上,(2x-4)(3-x)=;
解得;
(3)当x>3时,点M在线段OC上,点N在线段OD上,(2x-4)(x-3)=;
解得或x=s.
综上所述,出发后或s或时,△MON的面积为.
9. 解:(1)∵=1,
∴=1,即,
解得,
∵方程有两个不相等的实数根,
∴b2-4ac=[2(m-2)] 2-4(m2-3m+3)>0,
解得m<1,
又∵m不小于-1,
∴-1≤m<1,
∴m=,
将m=代入得,原式=-2;世纪*教育网
(2)
=
=
=
=
=
=-2(m-1)-m2
=-m2-2m+2
=-(m+1)2+3, om
∵-1≤m<1,
∴当m=-1时,有最大值,最大值是3.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
21.2.4 一元二次方程的根与系数的关系
知识梳理
1.一元二次方程根与系数的关系(韦达定理):设一元二次方程的两根是x1和x2,则 .21世纪教育网版权所有
2.当一元二次方程的两根是x1和x2时:
(1)若,则方程有 根;
(2)若,则方程有 个正根;
(3)若,则方程有 个负根.
重点突破
知识点 一元二次方程根与系数的关系
1.若x1、x2是一元二次方程x2+10x+16的两个根,则x1+x2的值是( )
A.-10 B.10 C.-16 D.16
【解析】本题主要考查利用根与系数的关系求两根之间关系的代数式的值。根据一元二次方程根与系数的关系得x1+x2=21cnjy.com
【答案】A
【点评】本题考查了根与系数的关系。
2.方程ax2+bx﹣c=0(a>0、b>0、c>0)的两个根的符号为( )
A.同号 B.异号 C.两根都为正 D.不能确定
【解析】本题主要考查利用根与系数的关系求方程中待定字母的值。首先由△=b2+4ac>0,可知方程有两个不等的实数根,再由x1x2=<0可知两根异号.www.21-cn-jy.com
【答案】B
3. 设x1、x2是一元二次方程x2﹣5x﹣1=0的两实数根,则2x1x2的值为________.
【解析】本题主要考查根与系数的关系知识的巧妙运用。首先根据根与系数的关系求出,再求出的值。解:∵x1、x2是一元二次方程x2﹣5x﹣1=0的两实数根,
∴x1+x2=5,x1x2=﹣1,∴2x1x2=﹣2,
【答案】-2.
基础过关
1.已知、是方程的两个实数根,那么下列结论正确的是( )
A.+=-1 B.+=-3 C.+=1 D. +=3
2.已知方程3x2-4x-4=0的两个实数根分别为x1,x2.则x1+x2=( )
A.-3 B. 3 C. D.
3.已知x1,x2是一元二次方程x2-4x+1=0的两个实数根,则x1x2等于( )
A.-4 B.-1 C.1 D.4
4.已知关于x的一元二次方程ax2+bx+c=0(a≠0)的两根互为相反数,则( )
A.b>0 B.b=0 C.b<0 D.c=0
5.已知关于x的一元二次方程x2-(m-1)x-(2m-2)=0的两根之和等于两根之积,则m的值为( )21·cn·jy·com
A.1 B.-1 C.2 D.-2
6.已知一元二次方程x2-x+2=0,则下列说法正确的是( )
A.两根之和为1 B.两根之积为2 C.两根的平方和为-3 D.没有实数根
7.已知实数x1,x2满足x1+x2=7,x1x2=12,则以x1,x2为根的一元二次方程是( )
A.x2﹣7x+12=0 B.x2+7x+12=0 C.x2+7x﹣12=0 D.x2﹣7x﹣12=0
8. 一元二次方程x2+px=2的两根为x1,x2,且x1=﹣2x2,则p的值为( )
A.2 B.1 C.1或﹣1 D.﹣1
9.已知一元二次方程2x2-5x+1=0的两根为m、n,则m2+n2= ___ _.
10.关于x的一元二次方程 ( http: / / www.21cnjy.com )的两个实数根分别为1和2,则 ( http: / / www.21cnjy.com ) , ( http: / / www.21cnjy.com ) .
11.已知 ( http: / / www.21cnjy.com )、 ( http: / / www.21cnjy.com )是方程 ( http: / / www.21cnjy.com )的两实数根,则 ( http: / / www.21cnjy.com )的值是 .
12.已知方程x2+mx+3=0的一个根是1,则它的另一个根是 ,m的值是 .
13.关于的一元二次方程=0的两实数根之积为负,则实数的取值范围是________.
14.已知关于x的一元二次方程有两个不相等的实数根、.
(1)求m的值;
(2)当时,求另一个根的值.
能力拓展
1.已知x1,x2是关于x的方程x2+ax-2b=0的两实数根,且x1+x2=-2,x1·x2=1,则ba的值是( )2·1·c·n·j·y
A. B.- C.4 D.-1
2.关于x的一元二次方程:x2—4x—m2=0有两个实数根x1,x2,则( )
A. B. C.4 D.-4
3.已知一元二次方程的两根分别是2和-3,则这个一元二次方程是( )
A.x2-6x+8=0 B.x2+2x-3=0 C.x2-x-6=0 D.x2+x-6=0
4.有两个一元二次方程:M:ax2+bx+c=0,N:cx2+bx+a=0,其中a·c≠0,a≠c,以下四个结论中,错误的是 ( )
A. 如果方程M有两个相等的实数根,那么方程N也有两个相等的实数根
B. 如果方程M有两根符号相同,那么方程N的两根符号也相同
C. 如果5是方程M的一个根,那么15是方程N的一个根
D. 如果方程M和方程N有一个相同的根,那么这个根必是x=1
5.一若关于x的一元二次方程x2-4x+k-3=0的两个实数根为x1,x2,且满足x1=3x2,试求出方程的两个实数根及k的值.2-1-c-n-j-y
6.关于的一元二次方程有两个不等实根、.
(1)求实数的取值范围;
(2)若方程两实根、满足,求的值.
7.已知关于x的一元二次方程x2-6x+(2m+1)=0有实数根.
①求m的取值范围;
②如果方程的两个实数根为x1,x2,且2x1x2+x1+x2≥20,求m的取值范围.
8.如图,菱形ABCD中,AC,BD交于O,AC=8m,BD=6m,动点M从A出发沿AC方向以2m/s匀速直线运动到C,动点N从B出发沿BD方向以1m/s匀速直线运动到D,若M,N同时出发,问出发后几秒钟时,△MON的面积为
【来源:21·世纪·教育·网】
9.设m是不小于-1的实数,使得关于x的 ( http: / / www.21cnjy.com )方程x2+2(m-2)x+m2-3m+3=0有两个不相等的实数根x1,x2.www.21-cn-jy.com21·世纪*教育网
(1)若,求的值;
(2)求的最大值.
参考答案
知识梳理
1..
2.一正一负,2,2
基础过关
1.B
2.D
3.C
4.B
5.A
6.D
7.A
8.C
9.
10.-3,2
11.10
12.3,-4
13.
14. 解:(1)∵一元二次方程有两个不相等的实数根,
∴,∴,∴.
(2)根据一元二次方程根与系数的关系,得,,∴.
能力拓展
1.A
2.D
3.D
4.D
5.解:由根与系数的关系,得 ( http: / / www.21cnjy.com )
又∵x1=3x2,③,
联立①、③,解方程组,得 ( http: / / www.21cnjy.com )
∴k=x1x2+3=3×1+3=6.
答:方程两根为x1=3,x2=1;k=6.
6.解:(1)∵原方程有两个不相等的实数根,
∴, 解得: .
(2)由根与系数的关系,得, .
∵,
∴,
解得:或,
又∵,
∴.
7.解:①根据题意得b2-4ac=(-6)2-4(2m+1)≥0,解得m≤4;
②根据题意得x1+x2=6,x1x2=2m ( http: / / www.21cnjy.com )+1,而2x1x2+x1+x2≥20,所以2(2m+1)+6≥20,解得m≥3,而m≤4,所以m的取值范围为3≤m≤421教育网
8.解:设解:设出发后x秒时,
(1)当x<2时,点M在线段AO上,点N在线段BO上.(4-2x)(3-x)=;
解得x1=,x2=
∵x<2,
∴;
(2)当2<x<3时,点M在线段OC上,点N在线段BO上,(2x-4)(3-x)=;
解得;
(3)当x>3时,点M在线段OC上,点N在线段OD上,(2x-4)(x-3)=;
解得或x=s.
综上所述,出发后或s或时,△MON的面积为.
9. 解:(1)∵=1,
∴=1,即,
解得,
∵方程有两个不相等的实数根,
∴b2-4ac=[2(m-2)] 2-4(m2-3m+3)>0,
解得m<1,
又∵m不小于-1,
∴-1≤m<1,
∴m=,
将m=代入得,原式=-2;世纪*教育网
(2)
=
=
=
=
=
=-2(m-1)-m2
=-m2-2m+2
=-(m+1)2+3, om
∵-1≤m<1,
∴当m=-1时,有最大值,最大值是3.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
