22.1.3 二次函数y=a(x-h)2+k的图象和性质学案(附答案)
文档属性
| 名称 | 22.1.3 二次函数y=a(x-h)2+k的图象和性质学案(附答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 890.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-06 00:00:00 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
22.1.3 二次函数的图象和性质
知识梳理
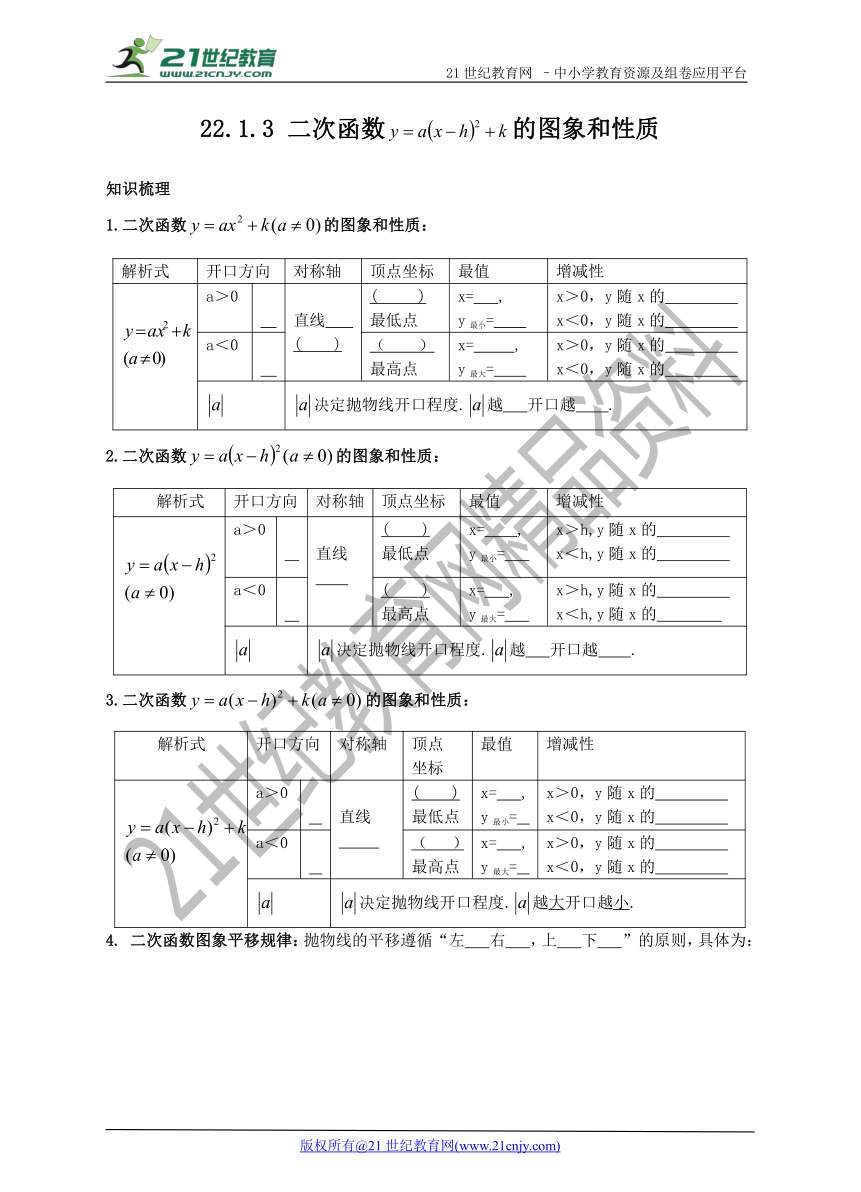
1.二次函数的图象和性质:
解析式 开口方向 对称轴 顶点坐标 最值 增减性
a>0 直线 ( ) ( )最低点 x= ,y最小= x>0,y随x的 x<0,y随x的
a<0 ( )最高点 x= ,y最大= x>0,y随x的 x<0,y随x的
决定抛物线开口程度.越 开口越 .
2.二次函数的图象和性质:
解析式 开口方向 对称轴 顶点坐标 最值 增减性
a>0 直线 ( )最低点 x= ,y最小= x>h,y随x的 x<h,y随x的
a<0 ( )最高点 x= ,y最大= x>h,y随x的 x<h,y随x的
决定抛物线开口程度.越 开口越 .
3.二次函数的图象和性质:
解析式 开口方向 对称轴 顶点坐标 最值 增减性
a>0 直线 ( )最低点 x= ,y最小= x>0,y随x的 x<0,y随x的
a<0 ( )最高点 x= ,y最大= x>0,y随x的 x<0,y随x的
决定抛物线开口程度.越大开口越小.
4. 二次函数图象平移规律:抛物线的平移遵循“左 右 ,上 下 ”的原则,具体为:
重点突破
知识点一 二次函数的性质
1.抛物线y = 3(x 2)2+4的开口方向、对称轴、顶点坐标分别为( )
A.开口向下,对称轴为x = 2,顶点坐标为( 2,4)
B.开口向上,对称轴为x = 2,顶点坐标为(2,4)
C.开口向上,对称轴为x = 2,顶点坐标为(2, 4)
D.开口向下,对称轴为x = 2,顶点坐标为(2,4)
【解析】本题主要考查二次函数的基本性质,熟练掌握二次函数的基本性质是解题的关键。此题对照顶点式,a=-3,h=2,k=4.所以开口向下,对称轴轴为x=2,顶点坐标为(2,4)
【答案】D
2.二次函数的最小值为 .
【解析】本题主要考查二次函数的基本性质—最值问题,解题的关键是掌握二次函数的性质.此题根据函数的表示形式可直接读出图象的顶点坐标,即可得到答案.∵a=2,抛物线开口向上,顶点位置最低,∴这个二次函数有最小值.当x=3时,y的最小值为-4.故答案为-4.
【答案】-4
知识点二 二次函数图象的平移规律
1. ( cm )将抛物线先向左平移2个单位长度,再向下平移3个单位长度得到抛物线对应的函数解析式是( )
A. B.
C. D.
【解析】本题主要考查二次函数图象的平移,解题的关键是掌握二次函数图象的平移规律.按照“左加右减、上加下减”的变换方式先把x变为x-2,再整体-3.即,故选择B.
【答案】B
基础过关
1.二次函数和,以下说法:①它们的图象都是开口向上;
②它们的对称轴都是轴,顶点坐标都是原点(0,0);
③当时,它们的函数值都是随着的增大而增大;
④它们的开口的大小是一样的.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
2.一次函数和二次函数的图象大致所示中的( )
A B. C. D.
3.如图,在平面直角坐标系中,抛物线所表示的函数解析式为y=-2(x-h)2+k,则下列结论正确的是( )
A.h>0,k>0 B.h<0,k>0 C.h<0,k<0 D.h>0,k<0
4.抛物线y=2(x-3)2+1的顶点坐标是( )
A.(3,1) B. (3,-1) C. (-3,1) D. (-3,-1)
5.若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则所得抛物线的解析式为( )
A.y=(x+2)2+3 B.y=(x-2)2+3 C.y=(x+2)2-3 D.y=(x-2)2-3
6.已知二次函数y=2(x-3)2+1.下列说法:①其图象的开口向下;②其图象的对称轴为直线x=-3;③其图象顶点坐标为(3,-1);④当x<3时,y随x的增大而减小.则其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
7.已知二次函数y=a(x-h)2+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是( )
A.6 B.5 C.4 D.3
8.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+a上的三点,则y1,y2,y3的大小关系为( )
A.y1>y2>y3 B.y1>y3>y2 C.y3>y2>y1 D.y3>y1>y2
9.已知点(x1,y1),(x2,y2)均在抛物线y=x2-1上,下列说法中正确的是( )
A.若y1=y2,则x1=x2 B.若x1=-x2,则y1=-y2
C.若0<x1<x2,则y1>y2 D.若x1<x2<0,则y1>y2
10.若抛物线y=-7(x+4)2-1平移得到y=-7x2,则必须( )
A.先向左平移4个单位,再向下平移1个单位
B.先向右平移4个单位,再向上平移1个单位
C.先向左平移1个单位,再向下平移4个单位
D.先向右平移1个单位,再向上平移4个单位
11.将二次三项式x2+4x+5化成(x+p)2+q的形式应为 .
12.将抛物线y=3(x-4)2+2向右平移1个单位长度,再向下平移3个单位长度,平移后的抛物线的解析式是____________.
13.如图,隧道的截图由抛物线和长方形构成,长方形的长是8 m,宽是2 m,抛物线可以用y=-x2+4表示.(1)一辆货运卡车高4 m,宽2 m,它能通过该隧道吗?(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过?
14.在直角坐标平面内,二次函数图象的顶点为A(1,-4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得的图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
能力拓展
1.如图,把抛物线y=x2沿直线y=x平移2个单位后,其顶点在直线上的A处,则平移后抛物线的解析式是( )
A.y=(x+1)2-1 B.y=(x+1)2+1 C.y=(x-1)2+1 D.y=(x-1)2-1
2.已知二次函数 在自变量x的值满足的情况下,与其对应的函数值y的最小值为5,则h的值为( )
A.1或-5 B.-1或5 C.1或-3 D.1或3
3.二次函数y=-(x-1)2+5,当m≤x≤n,且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( )
(A) (B)2 (C) (D)
4.如图,抛物线的顶点M在x轴上,抛物线与y轴交于点N,且OM=ON=4,矩形ABCD的顶点A、B在抛物线上,C、D在x轴上. (1)求抛物线的解析式;(2)设点A的横坐标为t(t>4),矩形ABCD的周长为 ,求与t之间函数关系式.
5.如图,在平面直角坐标系中,抛物线交轴于A,B两点(点A在点B的左侧),交轴于点W,顶点为C,抛物线的对称轴与轴的交点为D。
(1)求直线BC的解析式。
(2)点E(m,0),F(m+2,0)为轴上两点,其中,,F分别垂直于轴,交抛物线与点,,交BC于点M,N,当的值最大时,在轴上找一点R,使得值最大,请求出R点的坐标及的最大值。
6.如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.(1)求证:四边形EFGH是正方形;(2)判断直线EG是否经过一个定点,并说明理由;(3)求四边形EFGH面积的最小值.
参考答案
知识梳理
1.上,下,x=0,y轴,(0,k),(0,k),0,k,0,k,增大而增大,增大而减小,增大而减小,增大而增大,大,小
2. 上,下,x=h,(h,0),(h,0),h,0,h,0,增大而增大,增大而减小,增大而减小,增大而增大,大,小
3. 上,下,x=h,(h,k),(h,k),h,k,h,k,增大而增大,增大而减小,增大而减小,增大而增大,大,小
4. 加,减,加,减
基础过关
1.B
2.B
3.A
4.A
5.B
6.A
7.D
8.A
9.D
10.B
11.(x+2)2+1
12. y=3(x-5)2-1
13. 解:(1)把y=4-2=2代入y=-x2+4得: 2=-x2+4, 解得x=±2,
∴此时可通过物体的宽度为2-(-2)=4>2,
∴能通过.
(2)∵货车上面有2 m在矩形上面,当y=2时 2=-x2+4,
解得x=±2,∵2>2,∴能通过.
14.解:(1)设二次函数的解析式为y=a(x-1)2-4.
∵二次函数的图象过点B(3,0),
∴0=4a-4,解得a=1.
∴二次函数的解析式为y=(x-1)2-4,
即y=x2-2x-3.
(2)令y=0,得x2-2x-3=0,
解得x1=3,x2=-1.
∴二次函数的图象与x轴的两个交点坐标分别为(3,0)和(-1,0).
∴二次函数的图象向右平移1个单位后经过坐标原点,平移后所得的图象与x轴的另一个交点的坐标为(4,0).
能力拓展
1.C
2. B
3.D
4. 解:(1)∵OM=ON=4
∴M(4,0),N(0,4)
设抛物线的解析式为y=a(x-4)2(a≠0)
把N(0,4)代入上式得
∴
(2)设
,
CD=2DM=2(t-4)
5.解:⑴
⑵
故:
当时,最大,
此时
∴
∴,
6.(1)证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG,
在△AEH、△BFE、△CGF和△DHG中,,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形;
(2)解:直线EG经过一个定点,这个定点为正方形的中心(AC、BD的交点);理由如下:
连接AC、EG,交点为O;如图所示:
∵四边形ABCD是正方形,
∴AB∥CD,
∴∠OAE=∠OCG,
在△AOE和△COG中,
∴△AOE≌△COG(AAS),
∴OA=OC,即O为AC的中点,
∵正方形的对角线互相平分,
∴O为对角线AC、BD的交点,即O为正方形的中心;
(3)解:设四边形EFGH面积为S,设BE=xcm,则BF=(8﹣x)cm,
根据勾股定理得:EF2=BE2+BF2=x2+(8﹣x)2,
∴S=x2+(8﹣x)2=2(x﹣4)2+32,
∵2>0,
∴S有最小值,
当x=4时,S的最小值=32,
∴四边形EFGH面积的最小值为32cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
22.1.3 二次函数的图象和性质
知识梳理
1.二次函数的图象和性质:
解析式 开口方向 对称轴 顶点坐标 最值 增减性
a>0 直线 ( ) ( )最低点 x= ,y最小= x>0,y随x的 x<0,y随x的
a<0 ( )最高点 x= ,y最大= x>0,y随x的 x<0,y随x的
决定抛物线开口程度.越 开口越 .
2.二次函数的图象和性质:
解析式 开口方向 对称轴 顶点坐标 最值 增减性
a>0 直线 ( )最低点 x= ,y最小= x>h,y随x的 x<h,y随x的
a<0 ( )最高点 x= ,y最大= x>h,y随x的 x<h,y随x的
决定抛物线开口程度.越 开口越 .
3.二次函数的图象和性质:
解析式 开口方向 对称轴 顶点坐标 最值 增减性
a>0 直线 ( )最低点 x= ,y最小= x>0,y随x的 x<0,y随x的
a<0 ( )最高点 x= ,y最大= x>0,y随x的 x<0,y随x的
决定抛物线开口程度.越大开口越小.
4. 二次函数图象平移规律:抛物线的平移遵循“左 右 ,上 下 ”的原则,具体为:
重点突破
知识点一 二次函数的性质
1.抛物线y = 3(x 2)2+4的开口方向、对称轴、顶点坐标分别为( )
A.开口向下,对称轴为x = 2,顶点坐标为( 2,4)
B.开口向上,对称轴为x = 2,顶点坐标为(2,4)
C.开口向上,对称轴为x = 2,顶点坐标为(2, 4)
D.开口向下,对称轴为x = 2,顶点坐标为(2,4)
【解析】本题主要考查二次函数的基本性质,熟练掌握二次函数的基本性质是解题的关键。此题对照顶点式,a=-3,h=2,k=4.所以开口向下,对称轴轴为x=2,顶点坐标为(2,4)
【答案】D
2.二次函数的最小值为 .
【解析】本题主要考查二次函数的基本性质—最值问题,解题的关键是掌握二次函数的性质.此题根据函数的表示形式可直接读出图象的顶点坐标,即可得到答案.∵a=2,抛物线开口向上,顶点位置最低,∴这个二次函数有最小值.当x=3时,y的最小值为-4.故答案为-4.
【答案】-4
知识点二 二次函数图象的平移规律
1. ( cm )将抛物线先向左平移2个单位长度,再向下平移3个单位长度得到抛物线对应的函数解析式是( )
A. B.
C. D.
【解析】本题主要考查二次函数图象的平移,解题的关键是掌握二次函数图象的平移规律.按照“左加右减、上加下减”的变换方式先把x变为x-2,再整体-3.即,故选择B.
【答案】B
基础过关
1.二次函数和,以下说法:①它们的图象都是开口向上;
②它们的对称轴都是轴,顶点坐标都是原点(0,0);
③当时,它们的函数值都是随着的增大而增大;
④它们的开口的大小是一样的.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
2.一次函数和二次函数的图象大致所示中的( )
A B. C. D.
3.如图,在平面直角坐标系中,抛物线所表示的函数解析式为y=-2(x-h)2+k,则下列结论正确的是( )
A.h>0,k>0 B.h<0,k>0 C.h<0,k<0 D.h>0,k<0
4.抛物线y=2(x-3)2+1的顶点坐标是( )
A.(3,1) B. (3,-1) C. (-3,1) D. (-3,-1)
5.若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则所得抛物线的解析式为( )
A.y=(x+2)2+3 B.y=(x-2)2+3 C.y=(x+2)2-3 D.y=(x-2)2-3
6.已知二次函数y=2(x-3)2+1.下列说法:①其图象的开口向下;②其图象的对称轴为直线x=-3;③其图象顶点坐标为(3,-1);④当x<3时,y随x的增大而减小.则其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
7.已知二次函数y=a(x-h)2+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是( )
A.6 B.5 C.4 D.3
8.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+a上的三点,则y1,y2,y3的大小关系为( )
A.y1>y2>y3 B.y1>y3>y2 C.y3>y2>y1 D.y3>y1>y2
9.已知点(x1,y1),(x2,y2)均在抛物线y=x2-1上,下列说法中正确的是( )
A.若y1=y2,则x1=x2 B.若x1=-x2,则y1=-y2
C.若0<x1<x2,则y1>y2 D.若x1<x2<0,则y1>y2
10.若抛物线y=-7(x+4)2-1平移得到y=-7x2,则必须( )
A.先向左平移4个单位,再向下平移1个单位
B.先向右平移4个单位,再向上平移1个单位
C.先向左平移1个单位,再向下平移4个单位
D.先向右平移1个单位,再向上平移4个单位
11.将二次三项式x2+4x+5化成(x+p)2+q的形式应为 .
12.将抛物线y=3(x-4)2+2向右平移1个单位长度,再向下平移3个单位长度,平移后的抛物线的解析式是____________.
13.如图,隧道的截图由抛物线和长方形构成,长方形的长是8 m,宽是2 m,抛物线可以用y=-x2+4表示.(1)一辆货运卡车高4 m,宽2 m,它能通过该隧道吗?(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过?
14.在直角坐标平面内,二次函数图象的顶点为A(1,-4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得的图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
能力拓展
1.如图,把抛物线y=x2沿直线y=x平移2个单位后,其顶点在直线上的A处,则平移后抛物线的解析式是( )
A.y=(x+1)2-1 B.y=(x+1)2+1 C.y=(x-1)2+1 D.y=(x-1)2-1
2.已知二次函数 在自变量x的值满足的情况下,与其对应的函数值y的最小值为5,则h的值为( )
A.1或-5 B.-1或5 C.1或-3 D.1或3
3.二次函数y=-(x-1)2+5,当m≤x≤n,且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( )
(A) (B)2 (C) (D)
4.如图,抛物线的顶点M在x轴上,抛物线与y轴交于点N,且OM=ON=4,矩形ABCD的顶点A、B在抛物线上,C、D在x轴上. (1)求抛物线的解析式;(2)设点A的横坐标为t(t>4),矩形ABCD的周长为 ,求与t之间函数关系式.
5.如图,在平面直角坐标系中,抛物线交轴于A,B两点(点A在点B的左侧),交轴于点W,顶点为C,抛物线的对称轴与轴的交点为D。
(1)求直线BC的解析式。
(2)点E(m,0),F(m+2,0)为轴上两点,其中,,F分别垂直于轴,交抛物线与点,,交BC于点M,N,当的值最大时,在轴上找一点R,使得值最大,请求出R点的坐标及的最大值。
6.如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.(1)求证:四边形EFGH是正方形;(2)判断直线EG是否经过一个定点,并说明理由;(3)求四边形EFGH面积的最小值.
参考答案
知识梳理
1.上,下,x=0,y轴,(0,k),(0,k),0,k,0,k,增大而增大,增大而减小,增大而减小,增大而增大,大,小
2. 上,下,x=h,(h,0),(h,0),h,0,h,0,增大而增大,增大而减小,增大而减小,增大而增大,大,小
3. 上,下,x=h,(h,k),(h,k),h,k,h,k,增大而增大,增大而减小,增大而减小,增大而增大,大,小
4. 加,减,加,减
基础过关
1.B
2.B
3.A
4.A
5.B
6.A
7.D
8.A
9.D
10.B
11.(x+2)2+1
12. y=3(x-5)2-1
13. 解:(1)把y=4-2=2代入y=-x2+4得: 2=-x2+4, 解得x=±2,
∴此时可通过物体的宽度为2-(-2)=4>2,
∴能通过.
(2)∵货车上面有2 m在矩形上面,当y=2时 2=-x2+4,
解得x=±2,∵2>2,∴能通过.
14.解:(1)设二次函数的解析式为y=a(x-1)2-4.
∵二次函数的图象过点B(3,0),
∴0=4a-4,解得a=1.
∴二次函数的解析式为y=(x-1)2-4,
即y=x2-2x-3.
(2)令y=0,得x2-2x-3=0,
解得x1=3,x2=-1.
∴二次函数的图象与x轴的两个交点坐标分别为(3,0)和(-1,0).
∴二次函数的图象向右平移1个单位后经过坐标原点,平移后所得的图象与x轴的另一个交点的坐标为(4,0).
能力拓展
1.C
2. B
3.D
4. 解:(1)∵OM=ON=4
∴M(4,0),N(0,4)
设抛物线的解析式为y=a(x-4)2(a≠0)
把N(0,4)代入上式得
∴
(2)设
,
CD=2DM=2(t-4)
5.解:⑴
⑵
故:
当时,最大,
此时
∴
∴,
6.(1)证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG,
在△AEH、△BFE、△CGF和△DHG中,,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形;
(2)解:直线EG经过一个定点,这个定点为正方形的中心(AC、BD的交点);理由如下:
连接AC、EG,交点为O;如图所示:
∵四边形ABCD是正方形,
∴AB∥CD,
∴∠OAE=∠OCG,
在△AOE和△COG中,
∴△AOE≌△COG(AAS),
∴OA=OC,即O为AC的中点,
∵正方形的对角线互相平分,
∴O为对角线AC、BD的交点,即O为正方形的中心;
(3)解:设四边形EFGH面积为S,设BE=xcm,则BF=(8﹣x)cm,
根据勾股定理得:EF2=BE2+BF2=x2+(8﹣x)2,
∴S=x2+(8﹣x)2=2(x﹣4)2+32,
∵2>0,
∴S有最小值,
当x=4时,S的最小值=32,
∴四边形EFGH面积的最小值为32cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
