23.1 图形的旋转学案（附答案）

21世纪教育网 –中小学教育资源及组卷应用平台
第二十三章 旋转
23.1图形的旋转
知识梳理
1.旋转的相关概念
（1）定义：把一个平面图形绕着平面内某一点O转动一个角度，叫做图形的 .点O叫做 ，转动的角叫做 .21cnjy.com
① 在旋转过程中是 ( http: / / www.21cnjy.com ) 的，它可以在图形的外部，也可以在图形的内部，还可以在图形上. 可以按顺时针方向转动，也可以按逆时针方向转动.
②将一个图形绕一个定点沿某个方向转动一个角度，意味着 .
③旋转三要素： ， ， .
（2）相关概念：旋转得到的图形能够与原图形 ( http: / / www.21cnjy.com )重合，我们就把能够重合的点叫做 ，能够重合的线段叫做 ，能够重合的角叫做 .2·1·c·n·j·y
（3）旋转的范围是 ，否则就形成立体图形，不是我们研究的范围，因此“ ”不可忽略.【来源：21·世纪·教育·网】
2.旋转的性质
（1）性质：
①对应点到旋转中心的距离 .
②对应点与旋转中心所连线段的夹角等于 .
③旋转前、后的图形 .
（2）旋转不改变图形的 和 ，只改变图形的 ，即旋转前后的两个图形一定 .21*cnjy*com
（3）经过旋转，图形上的每一点都绕旋转中心 ( http: / / www.21cnjy.com )沿相同的方向旋转 ，任意一对对应点与旋转中心的连线所成的角都是 ，对应点到旋转中心的距离 .
（4）分析旋转形成的方法:“ ”，即分析 ， ， .
（5）画旋转图形时容易忽视 ( http: / / www.21cnjy.com )对旋转方向的要求，除了旋转中心及旋转角之外，还应指明旋转方向 ，若无特别说明，则应考虑两种情况.【版权所有：21教育】
3.利用旋转性质作图：
（1）作一个图形的旋转图形的依据是旋转的性质：对应点到 距离相等，每组 都旋转相同的角度.21教育名师原创作品
（2）简单旋转作图一般步骤：
①找出图形的 .
②确定 、 和 .
③将关键点与旋转中心连接起来，然后按旋转方向分别将它们旋转一个角，得到关键点的 .
④按照原图形的顺序连接这些对应点，所得到的图形就是 .
（3）画旋转图形时，已知条件必须满足以下几点：
①基本图形；②旋转中心；③旋转角；④旋转方向.
重点突破
知识点一 旋转的定义
1.下列运动属于旋转的是（　　）
A.滚动过程中的篮球的滚动 B.钟表的钟摆的摆动
C.气球升空的运动 D.一个图形沿某直线对折的过程
【解析】本题主要考查旋转的定义. A. ( http: / / www.21cnjy.com )滚动过程中的篮球属于滚动，不是绕着某一个固定的点转动，不属旋转；B.钟表的钟摆的摆动，符合旋转变换的定义，属于旋转；C.气球升空的运动是平移，不属于旋转；D.一个图形沿某直线对折的过程是轴对称，不属于旋转．故选B.
【答案】B
知识点二 旋转性质的应用
1.如图，将△ABC绕点C按顺时针 ( http: / / www.21cnjy.com )方向旋转至△A′B′C，使点A′落在BC的延长线上．已知∠A=27°，∠B=40°，则∠ACB′=　　度．21世纪教育网版权所有
( http: / / www.21cnjy.com )
【解析】本题主要考查旋转的性质，解决本题的关键是由旋转得到△ABC≌△A′B′C．
先根据三角形外角的性质求出∠ACA ( http: / / www.21cnjy.com )′=67°，再由△ABC绕点C按顺时针方向旋转至△A′B′C，得到△ABC≌△A′B′C，证明∠BCB′=∠ACA′，利用平角即可解答．
【答案】 46
2.如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（﹣2，5）的对应点A′的坐标是（　　）2-1-c-n-j-y
( http: / / www.21cnjy.com )
A.（2，5） B.（5，2） C.（2，﹣5） D.（5，﹣2）
【解析】本题主要考查旋转性质的应用. 由线段 ( http: / / www.21cnjy.com )AB绕点O顺时针旋转90°得到线段A′B′可以得出△ABO≌△A′B′O′，∠AOA′=90°，作AC⊥y轴于C，A′C′⊥x轴于C′，就可以得出△ACO≌△A′C′O，就可以得出AC=A′C′，CO=C′O，由A的坐标就可以求出结论，即A′（5，2）．21*cnjy*com
【答案】B．
知识点三 利用旋转的性质作图
1.如图，在方格纸上，以格 ( http: / / www.21cnjy.com )点连线为边的三角形叫做格点三角形，请按要求完成下列操作：先将格点△ABC绕A点逆时针旋转90°得到△A1B1C1，再将△A1B1C1沿直线B1C1作轴对称得到△A2B2C2.www.21-cn-jy.com
( http: / / www.21cnjy.com )
【解析】本题主要考查利用旋转、轴对称的性质作图，解答的关键是根据旋转、轴对称的性质准确的作出图形.
【答案】解：如图所示：
( http: / / www.21cnjy.com )
基础过关
1.下列现象中，不属于旋转的是（　　）
A.汽车在笔直的公路上行驶 B.大风车的转动
C.电风扇叶片的转动 D.时针的转动
2.规定：在平面内，将一 ( http: / / www.21cnjy.com )个图形绕着某一点旋转一定的角度（小于周角）后能和自身重合，则称此图形为旋转对称图形．下列图形是旋转对称图形，且有一个旋转角为60°的是（　　）
A． 正三角形 B．正方形 C．正六边形 D．正十边形
3.如图，将△ABC绕点A逆时针旋转一定角度，得到△ADE，若∠CAE=65°，∠E=70°，且AD⊥BC，则∠BAC的度数为（　　）【来源：21cnj*y.co*m】
A．60° B．75° C．85° D．90°
4.如图，正方形OABC的两边OA、O ( http: / / www.21cnjy.com )C分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是（　　）
( http: / / www.21cnjy.com )
A.（2，10） B.（﹣2，0）
C.（2，10）或（﹣2，0） D.（10，2）或（﹣2，0）
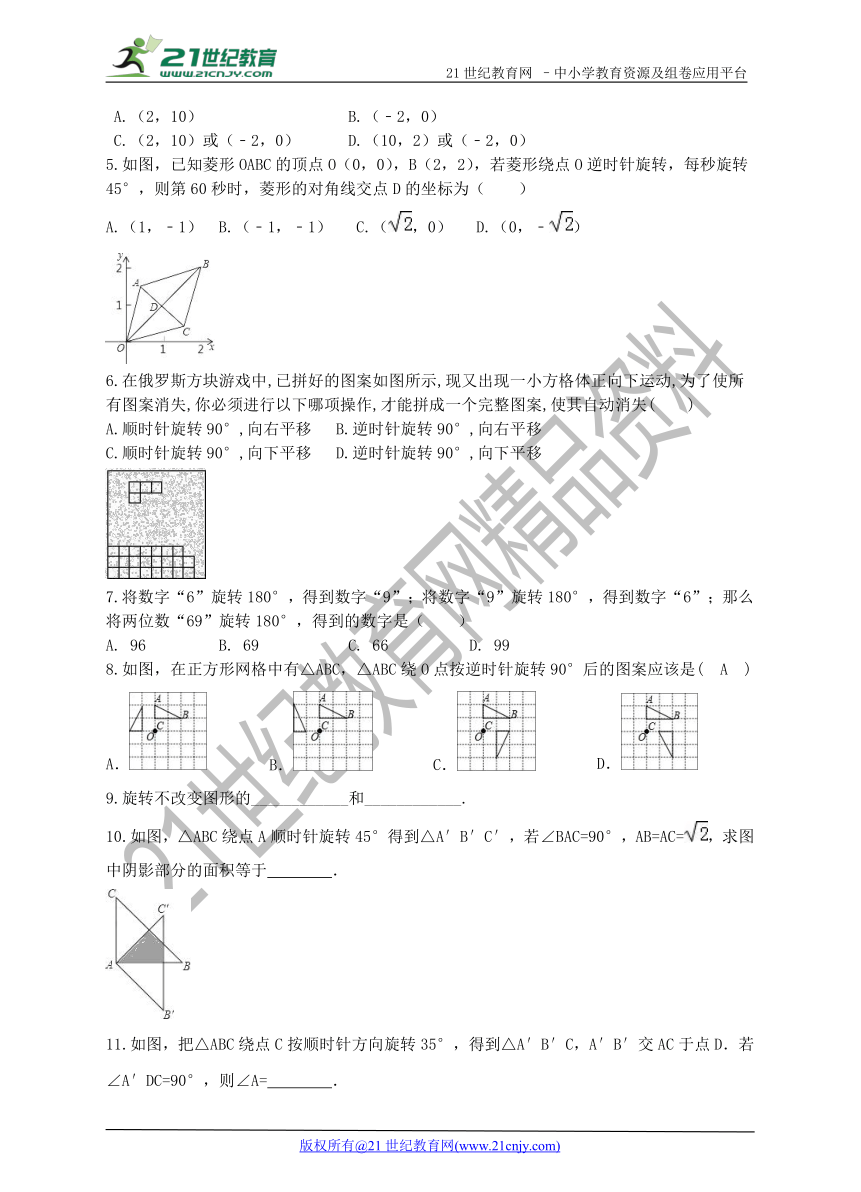
5.如图，已知菱形OABC的顶点O（0 ( http: / / www.21cnjy.com )，0），B（2，2），若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D的坐标为（　　）【出处：21教育名师】
A.（1，﹣1） B.（﹣1，﹣1） C.（ ( http: / / www.21cnjy.com )，0） D.（0，﹣ ( http: / / www.21cnjy.com )）
( http: / / www.21cnjy.com )
6.在俄罗斯方块游戏中,已拼好的图案如图所示,现又出现一小方格体正向下运动,为了使所
有图案消失,你必须进行以下哪项操作,才能拼成一个完整图案,使其自动消失( )
A.顺时针旋转90°,向右平移 B.逆时针旋转90°,向右平移
C.顺时针旋转90°,向下平移 D.逆时针旋转90°,向下平移
21·cn·jy·com
7.将数字“6”旋转180°，得到 ( http: / / www.21cnjy.com )数字“9”；将数字“9”旋转180°，得到数字“6”；那么将两位数“69”旋转180°，得到的数字是（　　）
A. 96 B. 69 C. 66 D. 99
8.如图，在正方形网格中有△ABC，△ABC绕O点按逆时针旋转90°后的图案应该是( A )
A． B． C． D．
9.旋转不改变图形的____________和____________.
10.如图，△ABC绕点A顺时针旋转45°得到△A′B′C′，若∠BAC=90°，AB=AC= ( http: / / www.21cnjy.com )，求图中阴影部分的面积等于 ．
( http: / / www.21cnjy.com )
11.如图，把△ABC绕点C按顺时针方向旋转35°，得到△A′B′C，A′B′交AC于点D．若∠A′DC=90°，则∠A=　 　．
( http: / / www.21cnjy.com )
12.如图，在平面直角坐标系xOy中，已知点A（3，4），将OA绕坐标原点O逆时针旋转90°至OA′，则点A′的坐标是 ．
13. 如图，已知Rt△ABC中，∠AB ( http: / / www.21cnjy.com )C=90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线平移至△FEG，DF、FG相交于点H．
（1）判断线段DE、FG的位置关系，并说明理由；
（2）连结CG，求证：四边形CBEG是正方形．
( http: / / www.21cnjy.com )
能力拓展
1.把一副三角板按如图放置，其中∠A ( http: / / www.21cnjy.com )BC ＝∠DEB＝90°，∠A ＝45°，∠D ＝30°，斜边AC＝BD＝10，若将三角板DEB绕点B逆时针旋转45°得到△D'E'B，则点A在△D'E'B的（　　）
A．内部 B．外部 C．边上 D．以上都有可能
( http: / / www.21cnjy.com )
2.有两个完全重合的矩形，将其中一个始 ( http: / / www.21cnjy.com )终保持不动，另一个矩形绕其对称中心O按逆时针方向进行旋转，每次均旋转45°，第1次旋转后得到图①，第2次旋转后得到图②，……，则第10次旋转后得到的图形与图①～④中相同的是（　　）21教育网
A．图① B．图② C．图③ D．图④
3.如图，在Rt△ABC中，∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△，点A在边上，则∠的大小为（　　）21·世纪*教育网
A．42° B．48° C．52° D．58°
4.在平面直角坐标系中，O为原 ( http: / / www.21cnjy.com )点，点A（4，0），点B（0，3），把△ABO绕点B逆时针旋转，得△A＇BO＇，点A、O旋转后的对应点为A＇、O＇，记旋转角为α.www-2-1-cnjy-com
（Ⅰ）如图①，若α=90°，求AA＇的长；
（Ⅱ）如图②，若α=120°，求点O＇的坐标；
（Ⅲ）在（Ⅱ）的条件下，边OA上的一点P旋转后的对应点是P＇，当O＇P+BP＇取得最小值时，求点P＇的坐标（直接写出结果即可）.
( http: / / www.21cnjy.com )
参考答案
知识梳理
1.（1）旋转.旋转中心，旋转角.
①旋转中心，静止不动，旋转方向.
②图形上每一个点同时按相同方向旋转相同的角度.
③旋转中心，旋转角，旋转方向.
（2）对应点，对应线段，对应角.
（3）在平面内，在平面内.
2.（1）①相等.②旋转角.③全等.
（2）大小，形状，位置，全等.
（3）相同的角度，旋转角，相等.
（4）三个一，一个中心，一个方向，一个角度.
（5）是顺时针还是逆时针.
3.（1）旋转中心,对应点
（2）关键点；旋转中心、旋转方向、旋转角；对应点.；旋转后的图形.
基础过关
1.A
2.C
3.C
4.C
5.B
6.A
7.B
8.A
9. 形状 大小
10. ( http: / / www.21cnjy.com )﹣1．
11.55°
12.（﹣4，3）
13. （1）解：FG⊥ED．理由如下：
∵△ABC绕点B顺时针旋转90°至△DBE后，
∴∠DEB=∠ACB，
∵把△ABC沿射线平移至△FEG，
∴∠GFE=∠A，
∵∠ABC=90°，
∴∠A+∠ACB=90°，
∴∠DEB+∠GFE=90°，
∴∠FHE=90°，
∴FG⊥ED；
（2）证明：根据旋转和平移可得∠GEF=90°，∠CBE=90°，CG∥EB，CB=BE，
∵CG∥EB，
∴∠BCG+∠CBE=90°，
∴∠BCG=90°，
∴四边形BCGE是矩形，
∵CB=BE，
∴四边形CBEG是正方形．
能力拓展
1.C
2.B
3.A
4.解：（Ⅰ）∵点A（4，0），点B（0，3），
∴OA=4，OB=3，
在Rt△AOB中，由勾股定理，得AB= ( http: / / www.21cnjy.com )=5，
根据题意，△A′BO′是△ABO绕点B逆时针旋转90°得到的，
由旋转的性质，可得∠ABA′=90°，A′B=AB=5，
在Rt△ABA′中，AA′= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )；
（Ⅱ）如图，根据题意，
由旋转的性质，可得∠O′BO=120°，O′B=OB=3，
过点O′作O′C⊥y轴于点C，则∠O′CB=90°，
在Rt△O′CB中，由∠O′BC=180°—120°=60°，得∠BO′C=180°—90°=30°
∴BC=O′B= ( http: / / www.21cnjy.com )，根据勾股定理得O′C= ( http: / / www.21cnjy.com )，
又OC=OB+BC= ( http: / / www.21cnjy.com )，
∴点O′的坐标为（ ( http: / / www.21cnjy.com )， ( http: / / www.21cnjy.com )）.
( http: / / www.21cnjy.com )
（Ⅲ）（ ( http: / / www.21cnjy.com )， ( http: / / www.21cnjy.com )）
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)