24.1.2 垂直于弦的直径学案(附答案)
文档属性
| 名称 | 24.1.2 垂直于弦的直径学案(附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 909.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-06 15:08:51 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
24.1.2 垂直于弦的直径
知识梳理
1.圆的对称性:
圆是 图形, 是它的对称中心;圆是 图形, 都是它的对称轴,有 条对称轴.
2.垂径定理及推论:
(1)定理:垂直于弦的直径 弦,并且 弦所对的两条弧.
用数学符号语言表示为(如下图):
∵CD过圆心,CD⊥AB于点P,
∴AP=PB、、.
(2)推论:平分弦( )的直径 弦,并且 弦所对的两条弧.用数学符号语言表示为:
∵AB不是直径,CD过圆心,AP=PB,
∴ CD⊥AB、、
3.其他:
圆中常作的辅助线是 作弦的垂线,垂径定理常用作计算,若圆的半径为r,一条弦长为a,圆心到弦的距离为d, 则r、a、d三者之间的关系式是 .
重点突破
知识点 垂径定理的应用
1.如图,在⊙O中,若弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.
【解析】本题主要考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
【答案】解:过点O作OE⊥AB于点E,连接OA
∵OE⊥弦AB,
∴AE= QUOTE \* MERGEFORMAT AB=4,
在Rt△OAE中,由勾股定理得,
OA2=AE2+OE2=42+32=25,
∴OA=5
2.如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D.
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
【解析】本题主要考查垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.(1)过O作OE⊥AB,根据垂径定理得到AE=BE,CE=DE,从而得到AC=BD;(2)由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,再根据勾股定理求出CE及AE的长,根据AC=AE﹣CE即可得出结论.
【答案】(1)证明:过点O作OE⊥AB于点E
∵AE=BE,CE=DE,
∴BE﹣DE=AE﹣CE,即AC=BD;
(2)解∵由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,∴OE=6,
∴CE=== ,AE===8,
∴AC=AE﹣CE=8﹣.
基础过关
1.如图所示,在☉O中,直径MN⊥弦AB,垂足为C,则下列结论中错误的是( )
A.AC=CB B.= C.= D.OC=CN
2.如图所示,⊙O的半径为13,弦AB的长度是24,,垂足为N,则( )
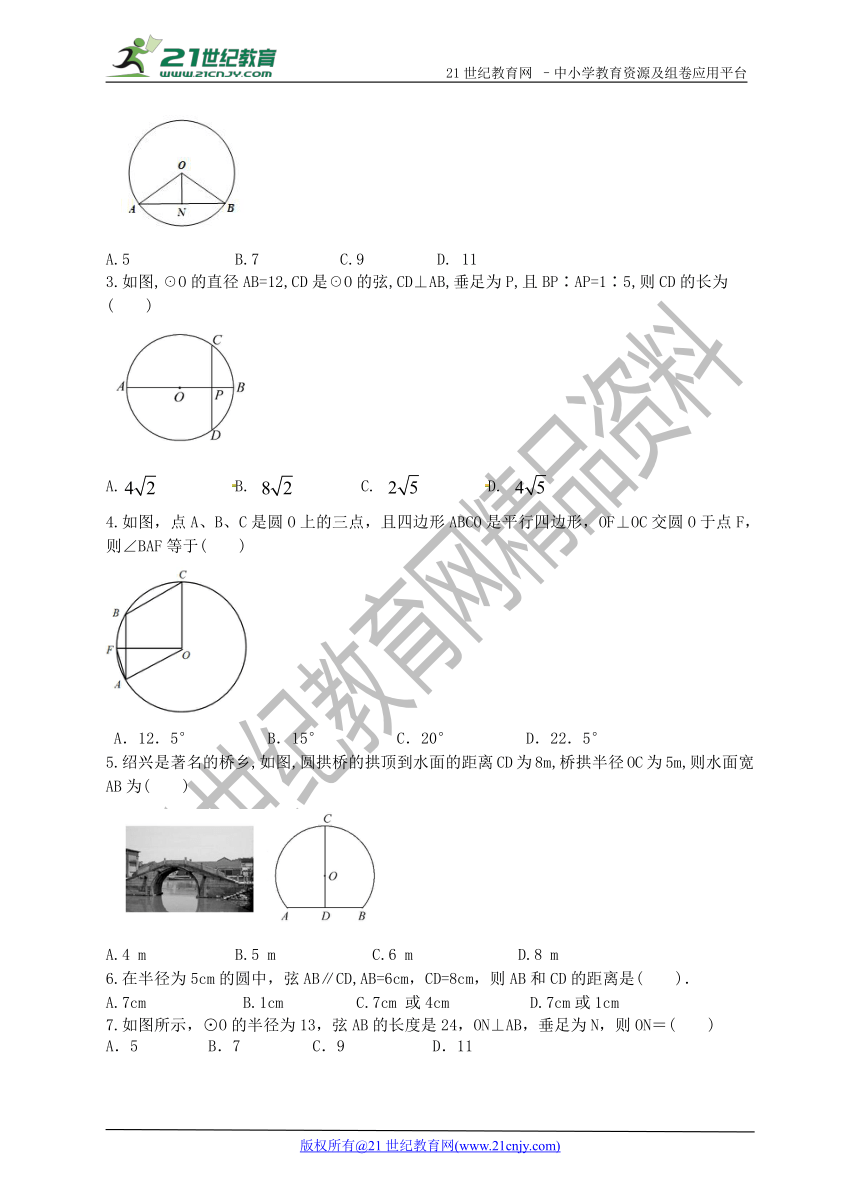
A.5 B.7 C.9 D. 11
3.如图,☉O的直径AB=12,CD是☉O的弦,CD⊥AB,垂足为P,且BP∶AP=1∶5,则CD的长为 ( )
A. B. C. D.
4.如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5° B.15° C.20° D.22.5°
5.绍兴是著名的桥乡,如图,圆拱桥的拱顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为( )
A.4 m B.5 m C.6 m D.8 m
6.在半径为5cm的圆中,弦AB∥CD,AB=6cm,CD=8cm,则AB和CD的距离是( ).
A.7cm B.1cm C.7cm 或4cm D.7cm或1cm
7.如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
A.5 B.7 C.9 D.11
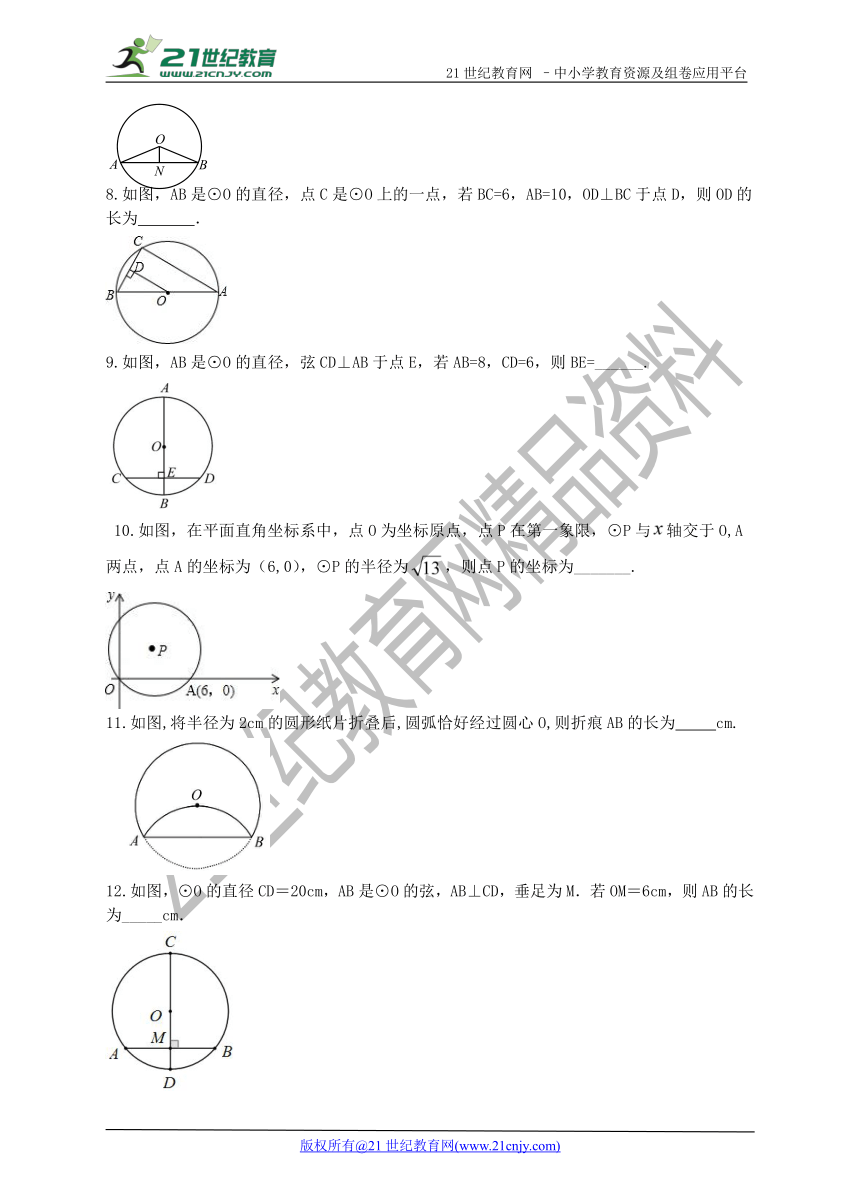
8.如图,AB是⊙O的直径,点C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为 .
9.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE=______.
10.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为,则点P的坐标为_______.
11.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为 cm.
12.如图,⊙O的直径CD=20cm,AB是⊙O的弦,AB⊥CD,垂足为M.若OM=6cm,则AB的长为_____cm.
能力拓展
1.已知☉O的直径CD=10cm,AB是☉O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )
A. cm B. cm C. cm或cm D. cm或cm
2.如图是由两个长方形组成的工件平面图(单位,mm),直线l是它的对称轴,能完全覆盖这个平面图形的圆面的最小半径是 mm.
3.如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若一直重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
参考答案
知识梳理
1.中心对称,圆心,轴对称,经过圆心的任何一条直径所在的直线,无数.
2.(1)平分,平分;(2)不是直径,垂直于,平分
3.过圆心,
基础过关
1.D
2.A
3.D
4.B
5.D
6.D
7.A
8.4
9.
10.(3,2)
11.
12.16
能力拓展
1.C
2.50
3.解:(1)过点A作AD⊥ON于点D,
∵∠NOM=30°,AO=80m,
∴AD=40m,
即对学校A的噪声影响最大时卡车P与学校A的距离为40米;
(2)由图可知:以50m为半径画圆,分别交ON于B,C两点,AD⊥BC,BD=CD=BC,OA=800m,
∵在Rt△AOD中,∠AOB=30°,
∴AD=OA=×800=400(m),
在Rt△ABD中,AB=50,AD=40,由勾股定理得:BD===30(m),
故BC=2×30=60米,即重型运输卡车在经过BD时对学校产生影响.
∵重型运输卡车的速度为18千米/小时,即=300(米/分钟),
∴重型运输卡车经过BD时需要60÷300=0.2(分钟).
答:卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为0.2分钟.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
24.1.2 垂直于弦的直径
知识梳理
1.圆的对称性:
圆是 图形, 是它的对称中心;圆是 图形, 都是它的对称轴,有 条对称轴.
2.垂径定理及推论:
(1)定理:垂直于弦的直径 弦,并且 弦所对的两条弧.
用数学符号语言表示为(如下图):
∵CD过圆心,CD⊥AB于点P,
∴AP=PB、、.
(2)推论:平分弦( )的直径 弦,并且 弦所对的两条弧.用数学符号语言表示为:
∵AB不是直径,CD过圆心,AP=PB,
∴ CD⊥AB、、
3.其他:
圆中常作的辅助线是 作弦的垂线,垂径定理常用作计算,若圆的半径为r,一条弦长为a,圆心到弦的距离为d, 则r、a、d三者之间的关系式是 .
重点突破
知识点 垂径定理的应用
1.如图,在⊙O中,若弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.
【解析】本题主要考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
【答案】解:过点O作OE⊥AB于点E,连接OA
∵OE⊥弦AB,
∴AE= QUOTE \* MERGEFORMAT AB=4,
在Rt△OAE中,由勾股定理得,
OA2=AE2+OE2=42+32=25,
∴OA=5
2.如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D.
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
【解析】本题主要考查垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.(1)过O作OE⊥AB,根据垂径定理得到AE=BE,CE=DE,从而得到AC=BD;(2)由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,再根据勾股定理求出CE及AE的长,根据AC=AE﹣CE即可得出结论.
【答案】(1)证明:过点O作OE⊥AB于点E
∵AE=BE,CE=DE,
∴BE﹣DE=AE﹣CE,即AC=BD;
(2)解∵由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,∴OE=6,
∴CE=== ,AE===8,
∴AC=AE﹣CE=8﹣.
基础过关
1.如图所示,在☉O中,直径MN⊥弦AB,垂足为C,则下列结论中错误的是( )
A.AC=CB B.= C.= D.OC=CN
2.如图所示,⊙O的半径为13,弦AB的长度是24,,垂足为N,则( )
A.5 B.7 C.9 D. 11
3.如图,☉O的直径AB=12,CD是☉O的弦,CD⊥AB,垂足为P,且BP∶AP=1∶5,则CD的长为 ( )
A. B. C. D.
4.如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5° B.15° C.20° D.22.5°
5.绍兴是著名的桥乡,如图,圆拱桥的拱顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为( )
A.4 m B.5 m C.6 m D.8 m
6.在半径为5cm的圆中,弦AB∥CD,AB=6cm,CD=8cm,则AB和CD的距离是( ).
A.7cm B.1cm C.7cm 或4cm D.7cm或1cm
7.如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
A.5 B.7 C.9 D.11
8.如图,AB是⊙O的直径,点C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为 .
9.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE=______.
10.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为,则点P的坐标为_______.
11.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为 cm.
12.如图,⊙O的直径CD=20cm,AB是⊙O的弦,AB⊥CD,垂足为M.若OM=6cm,则AB的长为_____cm.
能力拓展
1.已知☉O的直径CD=10cm,AB是☉O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )
A. cm B. cm C. cm或cm D. cm或cm
2.如图是由两个长方形组成的工件平面图(单位,mm),直线l是它的对称轴,能完全覆盖这个平面图形的圆面的最小半径是 mm.
3.如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若一直重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
参考答案
知识梳理
1.中心对称,圆心,轴对称,经过圆心的任何一条直径所在的直线,无数.
2.(1)平分,平分;(2)不是直径,垂直于,平分
3.过圆心,
基础过关
1.D
2.A
3.D
4.B
5.D
6.D
7.A
8.4
9.
10.(3,2)
11.
12.16
能力拓展
1.C
2.50
3.解:(1)过点A作AD⊥ON于点D,
∵∠NOM=30°,AO=80m,
∴AD=40m,
即对学校A的噪声影响最大时卡车P与学校A的距离为40米;
(2)由图可知:以50m为半径画圆,分别交ON于B,C两点,AD⊥BC,BD=CD=BC,OA=800m,
∵在Rt△AOD中,∠AOB=30°,
∴AD=OA=×800=400(m),
在Rt△ABD中,AB=50,AD=40,由勾股定理得:BD===30(m),
故BC=2×30=60米,即重型运输卡车在经过BD时对学校产生影响.
∵重型运输卡车的速度为18千米/小时,即=300(米/分钟),
∴重型运输卡车经过BD时需要60÷300=0.2(分钟).
答:卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为0.2分钟.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
