24.1.3 弧、弦、圆心角学案(附答案)
文档属性
| 名称 | 24.1.3 弧、弦、圆心角学案(附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-06 15:14:27 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
24.1.3 弧、弦、圆心角
知识梳理
1.圆心角定义:顶点在 的角叫做圆心角。
2.弧、弦、圆心角关系定理:
①在同圆或等圆中,相等的圆心角所对的 ( http: / / www.21cnjy.com ) 相等,所对的 也相等.用数学符号语言表示为: ∵∠AOB=∠A /OB/,∴ , .21世纪教育网版权所有
②在同圆或等圆中,如果两条弧相等,那么它们所对的 相等,所对的 也相等.用数学符号语言表示为: ∵ ( http: / / www.21cnjy.com ) = ( http: / / www.21cnjy.com ) ,∴ , .
③在同圆或等圆中,如果两条弦相等,那么它们 ( http: / / www.21cnjy.com )所对的 相等,所对的 也相等.用数学符号语言表示为: ∵AB=AˊBˊ, ∴ , .21教育网
( http: / / www.21cnjy.com )
3.其他:
(1)同圆或等圆中,两个圆心角、两条弧、两条弦中有 相等,就可以推出它们所对应的 也分别相等.这些结论是根据圆旋转的 得出,可归纳为圆心角相等 ( http: / / www.21cnjy.com )弧相等 ( http: / / www.21cnjy.com )弦相等.21·世纪*教育网
(2)推论中“弦相等”得出“所对的弧相等”,这里所对的弧指的是对应的劣弧与劣弧相等,优弧与优弧相等.www-2-1-cnjy-com
重点突破
知识点 弧、弦、圆心角关系定理
1.如图,在⊙O中,点C是 ( http: / / www.21cnjy.com )的中点,∠A=50°,则∠BOC=( )
( http: / / www.21cnjy.com )
A.40° B.45° C.50° D.60°
【解析】本题主要考查圆心角、弧、弦之间的关 ( http: / / www.21cnjy.com )系,等腰三角形的性质的应用,解题的关键是掌握圆心角、弧、弦之间的关系.①因为半径OA=OB,故可先根据等边对等角求得∠B的度数;②根据三角形内角和定理求得∠AOB的度数;③根据等弧所对圆心角相等求得∠BOC的度数.www.21-cn-jy.com
【答案】A
基础过关
1.下列图形中表示的角是圆心角的是( )
( http: / / www.21cnjy.com )
2.如图,在☉O中,=,∠A=30°,则∠B=( )
( http: / / www.21cnjy.com )
A.150° B.75° C.60° D.15°
3.已知M、N、P、Q四点的位置如图所示,下列结论中,正确的是( )
( http: / / www.21cnjy.com )
A. ∠NOQ=42 B. ∠NOP=132 C. ∠PON比∠MOQ大 D. ∠MOQ比∠MOP互补
4.在同圆中,圆心角∠AOB=2∠COD,则两条弧与的关系是( )
A.=2 B.>2 C.<2 D.不能确定
5.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是( )
A.51° B.56° C.68° D.78
6.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A.5πcm B.6πcm C.9πcm D.8πcm
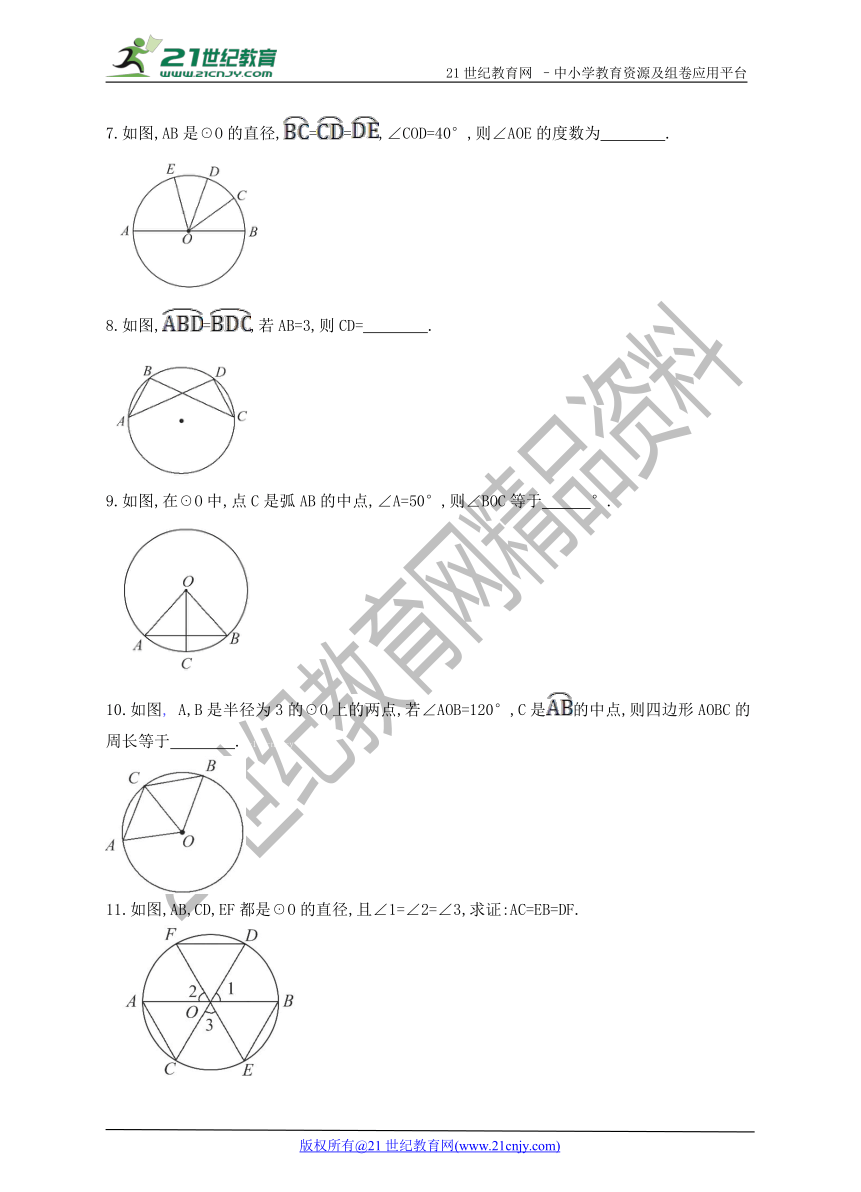
7.如图,AB是☉O的直径,==,∠COD=40°,则∠AOE的度数为 .
( http: / / www.21cnjy.com )
8.如图,=,若AB=3,则CD= .
( http: / / www.21cnjy.com )
9.如图,在☉O中,点C是弧AB的中点,∠A=50°,则∠BOC等于 °.
( http: / / www.21cnjy.com )
10.如图, A,B是半径为3的☉O上的两点,若∠AOB=120°,C是的中点,则四边形AOBC的周长等于 .2-1-c-n-j-y
( http: / / www.21cnjy.com )
11.如图,AB,CD,EF都是☉O的直径,且∠1=∠2=∠3,求证:AC=EB=DF.
( http: / / www.21cnjy.com )
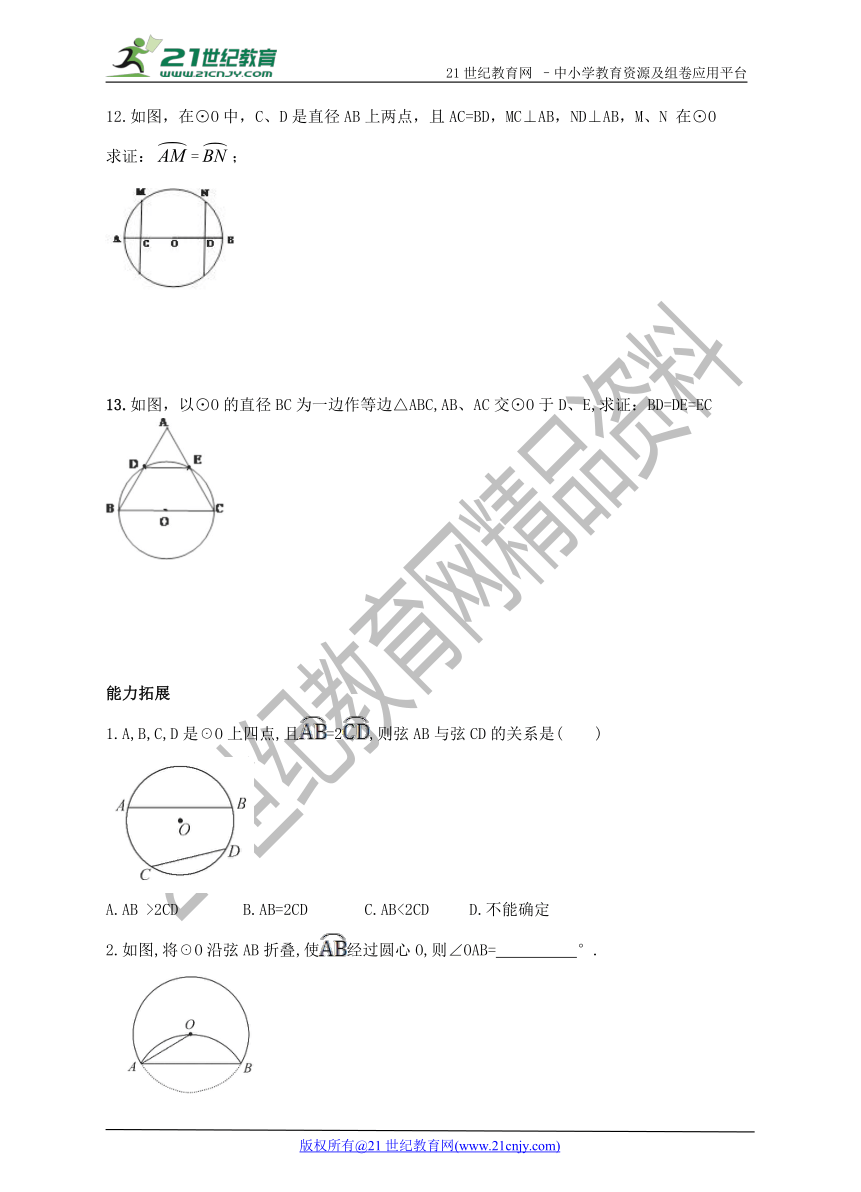
12.如图,在⊙O中,C、D是直径AB上两点,且AC=BD,MC⊥AB,ND⊥AB,M、N在⊙O
求证:=;
( http: / / www.21cnjy.com )
13.如图,以⊙O的直径BC为一边作等边△ABC,AB、AC交⊙O于D、E,求证:BD=DE=EC
( http: / / www.21cnjy.com )
能力拓展
1.A,B,C,D是☉O上四点,且=2,则弦AB与弦CD的关系是( )
( http: / / www.21cnjy.com )
A.AB >2CD B.AB=2CD C.AB<2CD D.不能确定21·cn·jy·com
2.如图,将☉O沿弦AB折叠,使经过圆心O,则∠OAB= °.
( http: / / www.21cnjy.com )
3.如图,已知OA,OB是☉O的半径,C为的中点,M,N分别是OA,OB的中点,求证:MC=NC.
( http: / / www.21cnjy.com ) [
4.如图,点A是半圆上的一个三等分点,点B是的中点,点P是直径MN上一个动点,圆O的半径为1.
( http: / / www.21cnjy.com )
(1)找出当AP+BP能得到最小值时点P的位置.
(2)求出AP+BP的最小值.
参考答案
知识梳理
1.圆心
2.弧,弦, ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ), AB=AˊBˊ ;圆心角,弦,∠AOB=∠AˊOBˊ ,AB=AˊBˊ ;圆心角,弧,∠AOB=∠AˊOBˊ , ( http: / / www.21cnjy.com ) = ( http: / / www.21cnjy.com ) .21cnjy.com
3.一组量,其余各组量,不变性.
基础过关
1.A
2.B
3.C
4.A
5.A
6.D
7.60°
8.3
9.40
10.12
11.证明:在☉O中,
∵AB,CD,EF都是☉O的直径,
∴∠AOC=∠1,∠ BOE=∠2,∠FOD=∠3.
∵∠1=∠2=∠3,
∴∠AOC=∠BOE=∠FOD.
∴ ( http: / / www.21cnjy.com ) QUOTE http://www.21cnjy.com/ ( http: / / www.21cnjy.com ) = QUOTE http://www.21cnjy.com/ ( http: / / www.21cnjy.com ) QUOTE http://www.21cnjy.com/ ( http: / / www.21cnjy.com ) = ( http: / / www.21cnjy.com )
∴AC=EB=DF.
12.证明:连结OM、ON,
( http: / / www.21cnjy.com )
∵OA=OB,AC=BD
∴OA-AC=OB-BD
即CO=DO
在Rt△OCM和Rt△ODN中,
OM=ON
OC=OD,
∴Rt△OCM≌Rt△ODN(HL),
∴∠AOM=∠BON,
∴
13.证明:连接OD、OE,
( http: / / www.21cnjy.com )
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵OB=OD,OE=OC,
∴△OBD、△OEC是等边三角形,
∴∠BOD=60°,∠EOC=60°
∴∠DOE=180°-∠BOD=∠EOC=60°,
∴∠BOD=∠DOE=∠EOC
∴BD=DE=EC
能力拓展
1.C
2.30
3.证明:连接OC.
∵C为的中点,
∴=,
∴∠MOC=∠NOC.
又∵M,N分别是OA,OB的中点,
∴OM=OA,ON=OB,
∴OM=ON.
在△OMC与△ONC中,
OM=ON
∠MOC=∠NOC
OC=OC,
∴△OMC≌△ONC,
∴MC=NC
4.解:(1)过A作AA′⊥MN于E,连接BA′.
( http: / / www.21cnjy.com )
∴P位于A′B与MN的交点处.
(2)∵点A是半圆上的一个三等分点,
∴∠AON=∠A′ON=60°,
∵点B是的中点,∴∠BON=30°,
∴∠BOA′=∠A′ON+∠BON=90°,
∵OB=OA′=1,
∴BA′=,即AP+BP最小值为.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
24.1.3 弧、弦、圆心角
知识梳理
1.圆心角定义:顶点在 的角叫做圆心角。
2.弧、弦、圆心角关系定理:
①在同圆或等圆中,相等的圆心角所对的 ( http: / / www.21cnjy.com ) 相等,所对的 也相等.用数学符号语言表示为: ∵∠AOB=∠A /OB/,∴ , .21世纪教育网版权所有
②在同圆或等圆中,如果两条弧相等,那么它们所对的 相等,所对的 也相等.用数学符号语言表示为: ∵ ( http: / / www.21cnjy.com ) = ( http: / / www.21cnjy.com ) ,∴ , .
③在同圆或等圆中,如果两条弦相等,那么它们 ( http: / / www.21cnjy.com )所对的 相等,所对的 也相等.用数学符号语言表示为: ∵AB=AˊBˊ, ∴ , .21教育网
( http: / / www.21cnjy.com )
3.其他:
(1)同圆或等圆中,两个圆心角、两条弧、两条弦中有 相等,就可以推出它们所对应的 也分别相等.这些结论是根据圆旋转的 得出,可归纳为圆心角相等 ( http: / / www.21cnjy.com )弧相等 ( http: / / www.21cnjy.com )弦相等.21·世纪*教育网
(2)推论中“弦相等”得出“所对的弧相等”,这里所对的弧指的是对应的劣弧与劣弧相等,优弧与优弧相等.www-2-1-cnjy-com
重点突破
知识点 弧、弦、圆心角关系定理
1.如图,在⊙O中,点C是 ( http: / / www.21cnjy.com )的中点,∠A=50°,则∠BOC=( )
( http: / / www.21cnjy.com )
A.40° B.45° C.50° D.60°
【解析】本题主要考查圆心角、弧、弦之间的关 ( http: / / www.21cnjy.com )系,等腰三角形的性质的应用,解题的关键是掌握圆心角、弧、弦之间的关系.①因为半径OA=OB,故可先根据等边对等角求得∠B的度数;②根据三角形内角和定理求得∠AOB的度数;③根据等弧所对圆心角相等求得∠BOC的度数.www.21-cn-jy.com
【答案】A
基础过关
1.下列图形中表示的角是圆心角的是( )
( http: / / www.21cnjy.com )
2.如图,在☉O中,=,∠A=30°,则∠B=( )
( http: / / www.21cnjy.com )
A.150° B.75° C.60° D.15°
3.已知M、N、P、Q四点的位置如图所示,下列结论中,正确的是( )
( http: / / www.21cnjy.com )
A. ∠NOQ=42 B. ∠NOP=132 C. ∠PON比∠MOQ大 D. ∠MOQ比∠MOP互补
4.在同圆中,圆心角∠AOB=2∠COD,则两条弧与的关系是( )
A.=2 B.>2 C.<2 D.不能确定
5.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是( )
A.51° B.56° C.68° D.78
6.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A.5πcm B.6πcm C.9πcm D.8πcm
7.如图,AB是☉O的直径,==,∠COD=40°,则∠AOE的度数为 .
( http: / / www.21cnjy.com )
8.如图,=,若AB=3,则CD= .
( http: / / www.21cnjy.com )
9.如图,在☉O中,点C是弧AB的中点,∠A=50°,则∠BOC等于 °.
( http: / / www.21cnjy.com )
10.如图, A,B是半径为3的☉O上的两点,若∠AOB=120°,C是的中点,则四边形AOBC的周长等于 .2-1-c-n-j-y
( http: / / www.21cnjy.com )
11.如图,AB,CD,EF都是☉O的直径,且∠1=∠2=∠3,求证:AC=EB=DF.
( http: / / www.21cnjy.com )
12.如图,在⊙O中,C、D是直径AB上两点,且AC=BD,MC⊥AB,ND⊥AB,M、N在⊙O
求证:=;
( http: / / www.21cnjy.com )
13.如图,以⊙O的直径BC为一边作等边△ABC,AB、AC交⊙O于D、E,求证:BD=DE=EC
( http: / / www.21cnjy.com )
能力拓展
1.A,B,C,D是☉O上四点,且=2,则弦AB与弦CD的关系是( )
( http: / / www.21cnjy.com )
A.AB >2CD B.AB=2CD C.AB<2CD D.不能确定21·cn·jy·com
2.如图,将☉O沿弦AB折叠,使经过圆心O,则∠OAB= °.
( http: / / www.21cnjy.com )
3.如图,已知OA,OB是☉O的半径,C为的中点,M,N分别是OA,OB的中点,求证:MC=NC.
( http: / / www.21cnjy.com ) [
4.如图,点A是半圆上的一个三等分点,点B是的中点,点P是直径MN上一个动点,圆O的半径为1.
( http: / / www.21cnjy.com )
(1)找出当AP+BP能得到最小值时点P的位置.
(2)求出AP+BP的最小值.
参考答案
知识梳理
1.圆心
2.弧,弦, ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ), AB=AˊBˊ ;圆心角,弦,∠AOB=∠AˊOBˊ ,AB=AˊBˊ ;圆心角,弧,∠AOB=∠AˊOBˊ , ( http: / / www.21cnjy.com ) = ( http: / / www.21cnjy.com ) .21cnjy.com
3.一组量,其余各组量,不变性.
基础过关
1.A
2.B
3.C
4.A
5.A
6.D
7.60°
8.3
9.40
10.12
11.证明:在☉O中,
∵AB,CD,EF都是☉O的直径,
∴∠AOC=∠1,∠ BOE=∠2,∠FOD=∠3.
∵∠1=∠2=∠3,
∴∠AOC=∠BOE=∠FOD.
∴ ( http: / / www.21cnjy.com ) QUOTE http://www.21cnjy.com/ ( http: / / www.21cnjy.com ) = QUOTE http://www.21cnjy.com/ ( http: / / www.21cnjy.com ) QUOTE http://www.21cnjy.com/ ( http: / / www.21cnjy.com ) = ( http: / / www.21cnjy.com )
∴AC=EB=DF.
12.证明:连结OM、ON,
( http: / / www.21cnjy.com )
∵OA=OB,AC=BD
∴OA-AC=OB-BD
即CO=DO
在Rt△OCM和Rt△ODN中,
OM=ON
OC=OD,
∴Rt△OCM≌Rt△ODN(HL),
∴∠AOM=∠BON,
∴
13.证明:连接OD、OE,
( http: / / www.21cnjy.com )
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵OB=OD,OE=OC,
∴△OBD、△OEC是等边三角形,
∴∠BOD=60°,∠EOC=60°
∴∠DOE=180°-∠BOD=∠EOC=60°,
∴∠BOD=∠DOE=∠EOC
∴BD=DE=EC
能力拓展
1.C
2.30
3.证明:连接OC.
∵C为的中点,
∴=,
∴∠MOC=∠NOC.
又∵M,N分别是OA,OB的中点,
∴OM=OA,ON=OB,
∴OM=ON.
在△OMC与△ONC中,
OM=ON
∠MOC=∠NOC
OC=OC,
∴△OMC≌△ONC,
∴MC=NC
4.解:(1)过A作AA′⊥MN于E,连接BA′.
( http: / / www.21cnjy.com )
∴P位于A′B与MN的交点处.
(2)∵点A是半圆上的一个三等分点,
∴∠AON=∠A′ON=60°,
∵点B是的中点,∴∠BON=30°,
∴∠BOA′=∠A′ON+∠BON=90°,
∵OB=OA′=1,
∴BA′=,即AP+BP最小值为.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
