24.1.4 圆周角学案（附答案）

21世纪教育网 –中小学教育资源及组卷应用平台
24.1.4圆周角
知识梳理
1.圆周角的定义：顶点在 ，两边都与圆 的角叫做圆周角.
2.圆周角定理及推论：
（1）在同圆或等圆中，同弧或等弧所对的圆周角 ，都等于这条弧所对的圆心角的 .
（2）半圆（或直径）所对的圆周角是 .
（3）900的圆周角所对的弦是 .
3.圆内接四边形：
（1）定义：如果一个四边形的所有顶点都在 上，这个多边形叫做 ，这个圆叫做这个四边形的 .21世纪教育网版权所有
（2）性质：圆内接四边形对角 .
重点突破
知识点一 圆周角定理及推论
1.如图，已知AB是⊙O的直径，∠D=40°，则∠CAB的度数为（ ）
( http: / / www.21cnjy.com )
A.20° B. 40° C. 50° D. 70°21·cn·jy·com
【解析】本题主要考查圆周角定理的推论，解题关键是掌握圆周角的相关性质．先由同弧所对的圆周角相等得出∠B的大小，再根据直径所对的圆周角是直角在△ABC中求出∠CAB的大小．∵，∴∠B＝∠D＝40°，∵AB为直径，∴∠ACB＝90°，∴∠CAB＝90°-40°=50°，故选择C.www.21-cn-jy.com
【答案】C
知识点二 圆内接四边形的性质
1.如图所示，四边形ABCD内接于⊙O，F是弧CD上一点，且，连接CF并延长交AD的延长线于点E，连接AC，若∠ABC=105°，∠BAC=25°，则∠E的度数为（ ）
A．45° B．50° C．55° D．60°
【解析】本题主要考查圆内接四边形及性质，解题的关键是掌握圆内接四边形的性质，并结合三角形内外角关系解决问题．①先利用圆的内接四边形对角互补的性质求出ACD的度数，②利用等弧所对的圆周角相等求出∠DCE，③利用三角形的一个外角等于不相邻两个内角的和求出∠E的度数.即∠E=∠ADC－∠DCE=75°－25°=50°，故选择B.2·1·c·n·j·y
【答案】B
基础过关
1.如图，在⊙O中， ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )，∠AOB=40°，则∠ADC的度数是（　　）
( http: / / www.21cnjy.com )
A．40° B．30° C．20° D．15°
2.如图4，C、D是以线段AB为直径的⊙O上两点，若CA=CD，且∠ACD=40°，则∠CAB= ( )．
A．10° B．20° C．30° D．40°
( http: / / www.21cnjy.com )
3.如图，已知AB是⊙O的直径，∠D=40°，则∠CAB的度数为（　　）
( http: / / www.21cnjy.com )
A．20° B．40° C．50° D．70°
4.如图，AB是⊙O的直径，BC是⊙O的弦，若∠OBC＝60°，则∠BAC的度数是（ ）
A.75° B. 60° C.45° D.30°
( http: / / www.21cnjy.com )
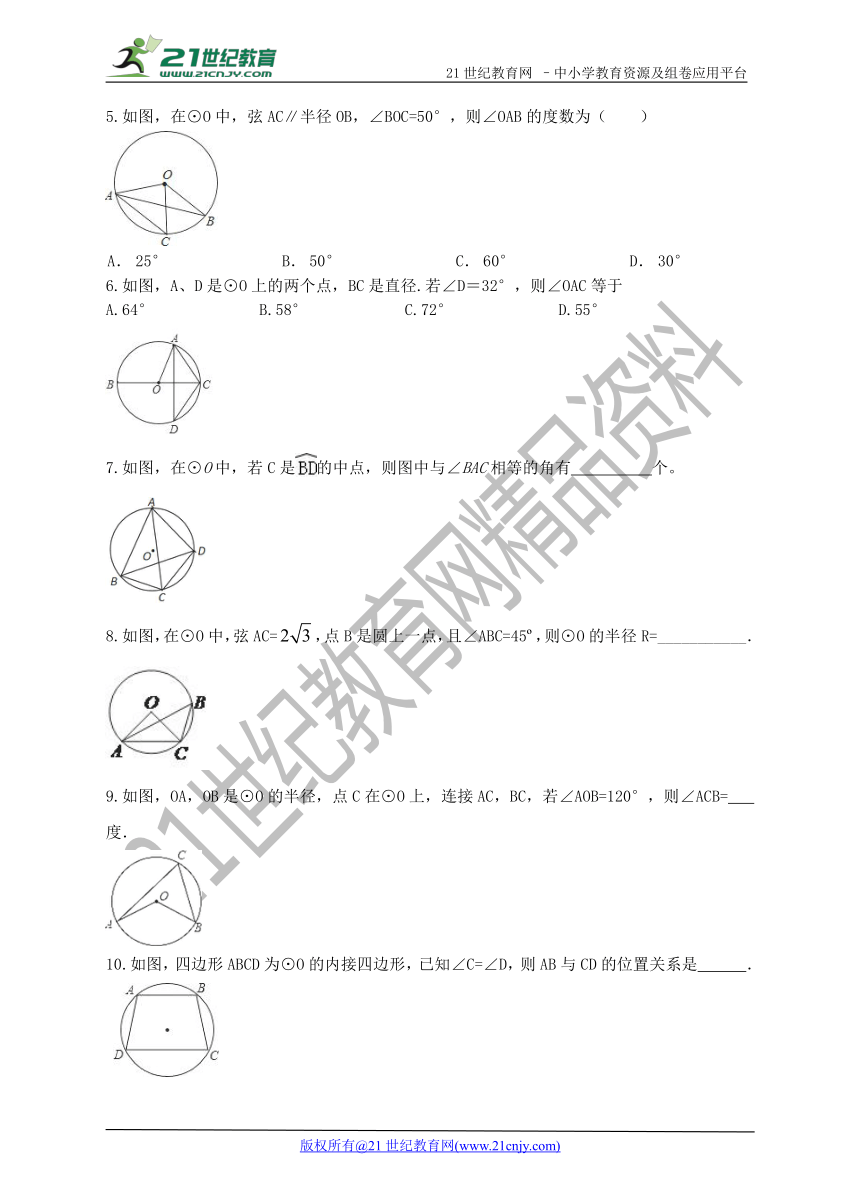
5.如图，在⊙O中，弦AC∥半径OB，∠BOC=50°，则∠OAB的度数为（　　）
( http: / / www.21cnjy.com )
　 A． 25° B． 50° C． 60° D． 30°
6.如图，A、D是⊙O上的两个点，BC是直径.若∠D＝32°，则∠OAC等于
A.64° B.58° C.72° D.55°
( http: / / www.21cnjy.com )
7.如图，在⊙O中，若C是 ( http: / / www.21cnjy.com )的中点，则图中与∠BAC相等的角有　　　　　个。
( http: / / www.21cnjy.com )
8.如图，在⊙O中，弦AC=，点B是圆上一点，且∠ABC=45 ，则⊙O的半径R=___________．
( http: / / www.21cnjy.com )
9.如图，OA，OB是⊙O的半径，点C在⊙O上，连接AC，BC，若∠AOB=120°，则∠ACB=　　度．
( http: / / www.21cnjy.com )
10.如图，四边形ABCD为⊙O的内接四边形，已知∠C=∠D，则AB与CD的位置关系是　　　．
( http: / / www.21cnjy.com )
11.如图，⊙C过原点，且与两坐标轴分别 ( http: / / www.21cnjy.com )交于点A，点B，点A的坐标为（0，3），M是第三象限内⊙C上一点，∠BMO=120°，则⊙C的半径为　　　　．【来源：21·世纪·教育·网】
12.如图，在⊙O中，圆心角∠AOB=70°，那么圆周角∠C= .
( http: / / www.21cnjy.com )
13.如图，在⊙O中，A，B是圆上的两点，已知∠AOB=40°，直径CD∥AB，连接AC，则∠BAC=______度．21·世纪*教育网
( http: / / www.21cnjy.com )
14.如图，四边形ABCD为⊙O的内接四边形，已知∠BCD =110°，则∠BAD =______度.
( http: / / www.21cnjy.com )
15.如图,在☉O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°，(1)求∠B的大小. (2)已知AD=6,求圆心O到BD的距离.www-2-1-cnjy-com
( http: / / www.21cnjy.com )
16.如图，已知BC为半圆O的直径，AB= ( http: / / www.21cnjy.com )AF,AC交BF于点M，过A点作AD⊥BC于D，交BF于E，则AE与BE的大小有什么关系？为什么？21*cnjy*com
( http: / / www.21cnjy.com )
能力拓展
1.如图，Rt△ABC的斜边AB与量角器的 ( http: / / www.21cnjy.com )直径恰好重合，B点与0刻度线的一端重合，∠ABC=40°，射线CD绕点C转动，与量角器外沿交于点D，若射线CD将△ABC分割出以BC为边的等腰三角形，则点D在量角器上对应的度数是（　　） 21教育网
( http: / / www.21cnjy.com )
A．40° B．70° C．70°或80° D．80°或140°
2.如图，AD、BC是⊙O ( http: / / www.21cnjy.com )的两条互相垂直的直径，点P从点O出发，沿O→C→D→O的路线匀速运动，设∠APB=y（单位：度），那么y与点P运动的时间x（单位：秒）的关系图是（ ）
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
3.如图，AB是○O的直径，C，D是○O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：2-1-c-n-j-y
①AD⊥BD；②∠AOC=∠AEC；③CB平分∠ABD；④AF=DF；⑤BD=2OF；⑥△CEF≌△BED，其中一定成立的是【来源：21cnj*y.co*m】
( http: / / www.21cnjy.com )
A．②④⑤⑥ B．①③⑤⑥ C．②③④⑥ D．①③④⑤
4.两圆相交于A,B两点,小圆经过大圆的圆心O,点C,D分别在两圆上,若∠ADB=100°,
则∠ACB的度数为　　　　　　．
( http: / / www.21cnjy.com )
5．如图,☉O的直径AB的长为6,弦AC的长为2,∠ACB的平分线交☉O于点D,求四边形ADBC的面积.【出处：21教育名师】
( http: / / www.21cnjy.com )
6. 如图，已知△ABC内接于⊙O，且 ( http: / / www.21cnjy.com )AB=AC，直径AD交BC于点E，F是OE上的一点，使CF∥BD．（1）求证：BE=CE；（2）试判断四边形BFCD的形状，并说明理由；（3）若BC=8，AD=10，求CD的长．21cnjy.com
( http: / / www.21cnjy.com )
参考答案
知识梳理
1.圆上，相交.
2.相等，一半；直角；直径.
3.同一个圆，圆内接四边形，外接圆；互补.
基础过关
1.C
2.B
3.C
4.D
5.A
6.B
7.3
8.
9.60 ．
10.AB∥CD．
11.3
12.35°
13.35
14.70°
15.解：(1)∵∠APD=∠C+∠CAB,
∴∠C=65°-40°=25°.
∴∠B=∠C=25°.
(2)过点O作OE⊥BD于E,则DE=BE.
( http: / / www.21cnjy.com )
又∵AO=BO,
∴OE=AD=×6=3.
∴圆心O到BD的距离为3.
16.解：AE=BE理由如下：
∵AB=AF
∴ ( http: / / www.21cnjy.com )=弧AF
∴∠ACB=∠ABF
∵BC为直径
∴∠BAC=90°即∠BAD+∠DAC=90°
∵AD⊥BC于D
∴∠DAC+∠ACD=90°
∴∠BAD=∠ACB
∴∠ABF=∠BAD
∴AE=BE
能力拓展
1.D
2.B
3.D
4.40°
5．解：∵AB是直径,∴∠ACB=∠ADB=90°.
在Rt△ABC中,AB=6,AC=2,
∴BC===4.
∵∠ACB的平分线交☉O于点D,
∴∠DCA=∠BCD,∴=,∴AD=BD,
∴在Rt△ABD中,AD=BD=AB=3,
∴四边形ADBC的面积=S△ABC+S△ABD
=AC·BC+AD·BD
=×2×4+×(3)2=9+4.
6.（1）证明：∵AD是直径，
∴∠ABD=∠ACD=90°，
在Rt△ABD和Rt△ACD中，
( http: / / www.21cnjy.com )，
∴Rt△ABD≌Rt△ACD，
∴∠BAD=∠CAD，
∵AB=AC，
∴BE=CE；
（2）四边形BFCD是菱形．
证明：∵AD是直径，AB=AC，
∴AD⊥BC，BE=CE，
∵CF∥BD，
∴∠FCE=∠DBE，
在△BED和△CEF中
( http: / / www.21cnjy.com )，
∴△BED≌△CEF，
∴CF=BD，
∴四边形BFCD是平行四边形，
∵∠BAD=∠CAD，
∴BD=CD，
∴四边形BFCD是菱形；
（3）解：∵AD是直径，AD⊥BC，BE=CE，
∴CE2=DE AE，
设DE=x，
∵BC=8，AD=10，
∴42=x（10﹣x），
解得：x=2或x=8（舍去）
在Rt△CED中，
CD= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com )．
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)