28.2.1解直角三角形 课件
图片预览



文档简介
课件16张PPT。28.2.1 解直角三角形献县第三中学
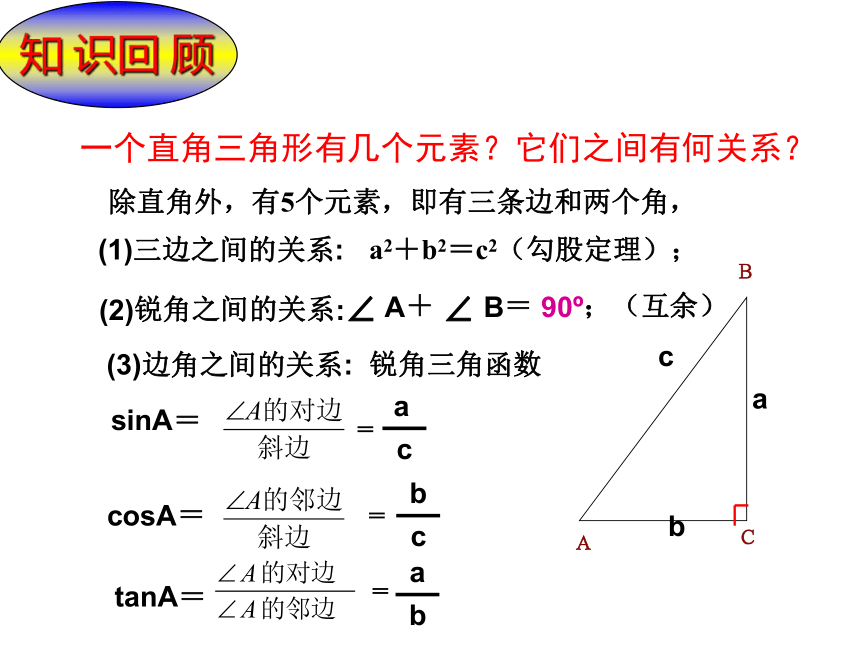
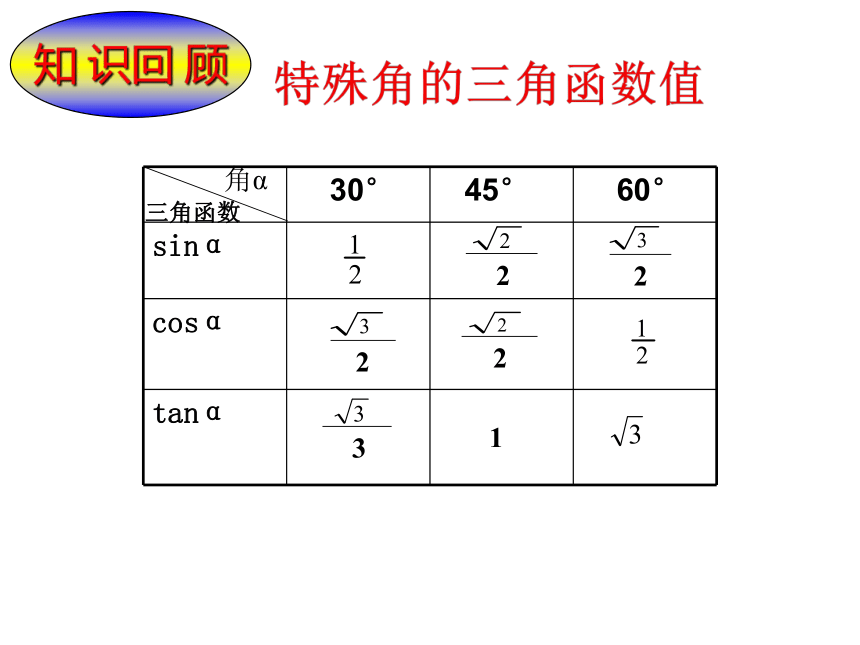
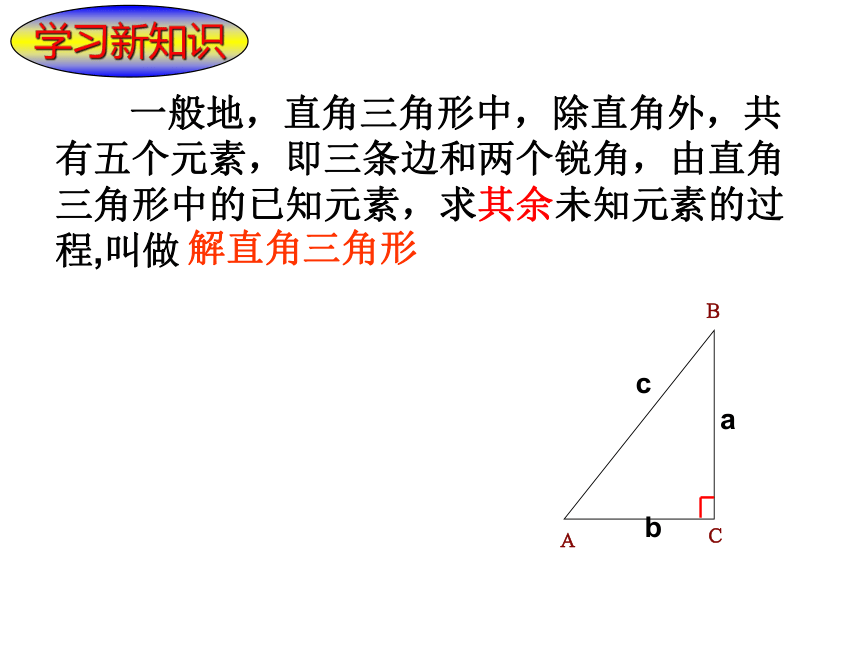
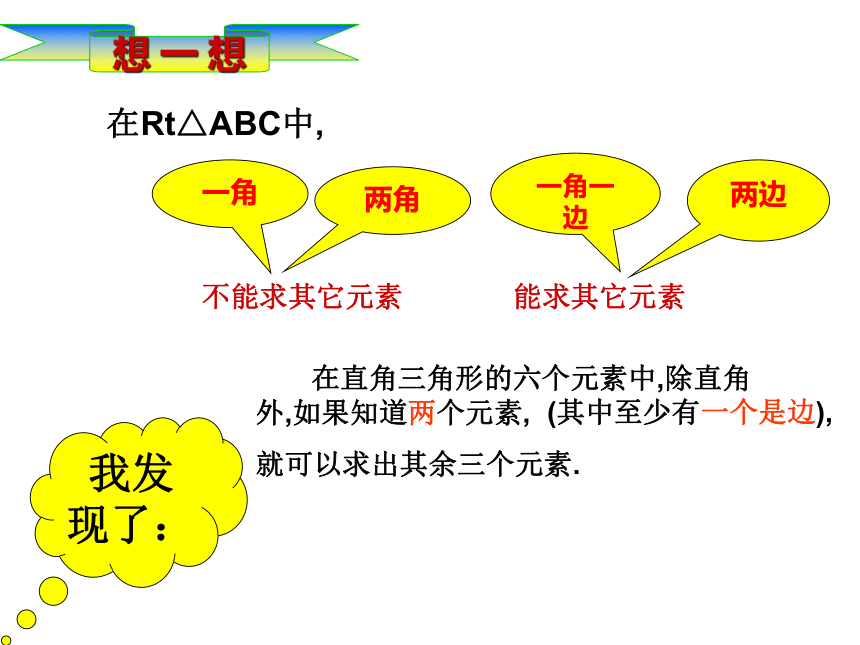
邢娇娇知 识回 顾一个直角三角形有几个元素?它们之间有何关系?(1)三边之间的关系:a2+b2=c2(勾股定理);(2)锐角之间的关系:∠ A+ ∠ B= 90o;(互余)(3)边角之间的关系:sinA=cosA=tanA=除直角外,有5个元素,即有三条边和两个角,锐角三角函数═══角α三角函数1知 识回 顾特殊角的三角函数值ABCBC=5.2mAB=54.5m 在本章引言中我们曾经描述过比萨斜塔倾斜程度的问题,把1972年的情形抽象为数学问题为:设塔顶中心点为B,塔身中心线与垂直中心线的夹角为∠A,过点B向垂直中心线引垂线,垂足为C(如图所示).在Rt△ABC中,∠C=90°,BC=5.2 m,AB=54.5 m,求∠A的度数.利用计算器可得∠A≈5°28′ 一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角,由直角三角形中的已知元素,求其余未知元素的过程,叫做解直角三角形学习新知识在Rt△ABC中,探究 你发现了什么?不能不能一角一角一边两角 (2)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗? (1)根据∠A= 60°,你能求出这个三角形的其他元素吗?∠B AC BC两边∠A ∠B AB在Rt△ABC中,(其中至少有一个是边),想 一 想一角一边两边两角不能求其它元素一角能求其它元素解直角三角形的依据锐角三角函数关系式的变形:·例1:在Rt△ABC中,∠C=90°,AC= ,BC= ,
解这个直角三角形.例题讲解解:∴∠A=60°,
∠B=90°— ∠A
= 90°— 60°
= 30°, ==例2:在Rt△ABC中,∠C=90°,∠B=35°,b=20,
解这个直角三角形.(精确到0.1)解:尽量选择原始数据,避免累积错误35°20???试一试你学会了吗?在Rt△ABC,∠C=90°,根据下列条件解直角三角形
(1)a=20 , b=20,
(2) ∠A=60°, b=4,
解题时要先把直角三角形画出来1.在Rt△ABC中,∠C=90 °,a,b,c分别是∠A,∠B,∠C的对边. 解这个直角三角形 补充练习∠BAC的平分线AD=42.在Rt△ABC中,∠C为直角,AC=6,,解此直角三角形。 补充练习60°30°61230° 3.在四边形ABCD中,∠A= ,AB⊥BC,AD⊥DC,AB=20cm,CD=10cm,求AD,BC的长(保留根号)? 60°补充练习E60°30°作业:课本第77页习题第1题。
《课时练》28.2.1解直角三角形
邢娇娇知 识回 顾一个直角三角形有几个元素?它们之间有何关系?(1)三边之间的关系:a2+b2=c2(勾股定理);(2)锐角之间的关系:∠ A+ ∠ B= 90o;(互余)(3)边角之间的关系:sinA=cosA=tanA=除直角外,有5个元素,即有三条边和两个角,锐角三角函数═══角α三角函数1知 识回 顾特殊角的三角函数值ABCBC=5.2mAB=54.5m 在本章引言中我们曾经描述过比萨斜塔倾斜程度的问题,把1972年的情形抽象为数学问题为:设塔顶中心点为B,塔身中心线与垂直中心线的夹角为∠A,过点B向垂直中心线引垂线,垂足为C(如图所示).在Rt△ABC中,∠C=90°,BC=5.2 m,AB=54.5 m,求∠A的度数.利用计算器可得∠A≈5°28′ 一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角,由直角三角形中的已知元素,求其余未知元素的过程,叫做解直角三角形学习新知识在Rt△ABC中,探究 你发现了什么?不能不能一角一角一边两角 (2)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗? (1)根据∠A= 60°,你能求出这个三角形的其他元素吗?∠B AC BC两边∠A ∠B AB在Rt△ABC中,(其中至少有一个是边),想 一 想一角一边两边两角不能求其它元素一角能求其它元素解直角三角形的依据锐角三角函数关系式的变形:·例1:在Rt△ABC中,∠C=90°,AC= ,BC= ,
解这个直角三角形.例题讲解解:∴∠A=60°,
∠B=90°— ∠A
= 90°— 60°
= 30°, ==例2:在Rt△ABC中,∠C=90°,∠B=35°,b=20,
解这个直角三角形.(精确到0.1)解:尽量选择原始数据,避免累积错误35°20???试一试你学会了吗?在Rt△ABC,∠C=90°,根据下列条件解直角三角形
(1)a=20 , b=20,
(2) ∠A=60°, b=4,
解题时要先把直角三角形画出来1.在Rt△ABC中,∠C=90 °,a,b,c分别是∠A,∠B,∠C的对边. 解这个直角三角形 补充练习∠BAC的平分线AD=42.在Rt△ABC中,∠C为直角,AC=6,,解此直角三角形。 补充练习60°30°61230° 3.在四边形ABCD中,∠A= ,AB⊥BC,AD⊥DC,AB=20cm,CD=10cm,求AD,BC的长(保留根号)? 60°补充练习E60°30°作业:课本第77页习题第1题。
《课时练》28.2.1解直角三角形
