人教版九年级数学上册24.1.4圆周角课件(24张ppt)
文档属性
| 名称 | 人教版九年级数学上册24.1.4圆周角课件(24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 268.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-08 11:18:10 | ||
图片预览

文档简介
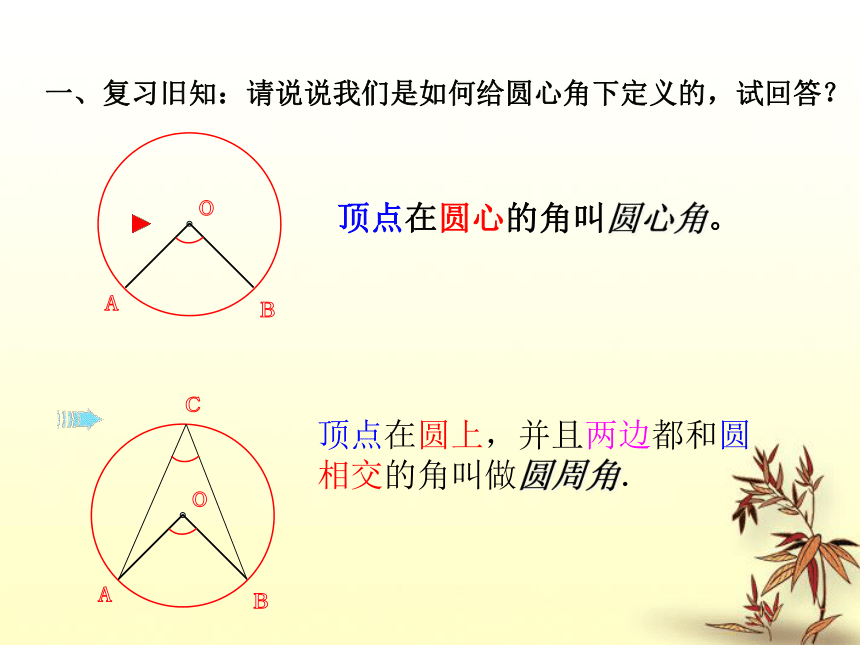
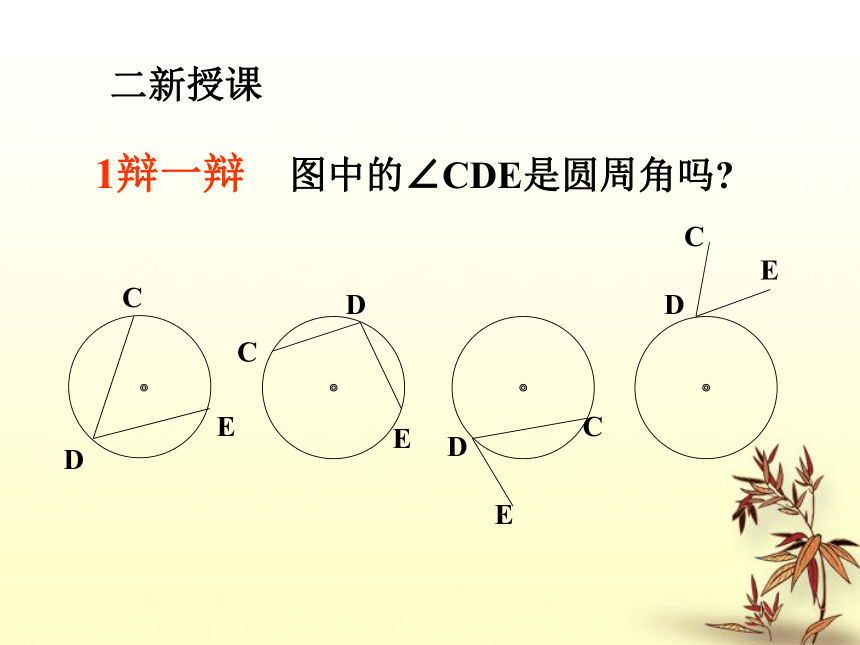
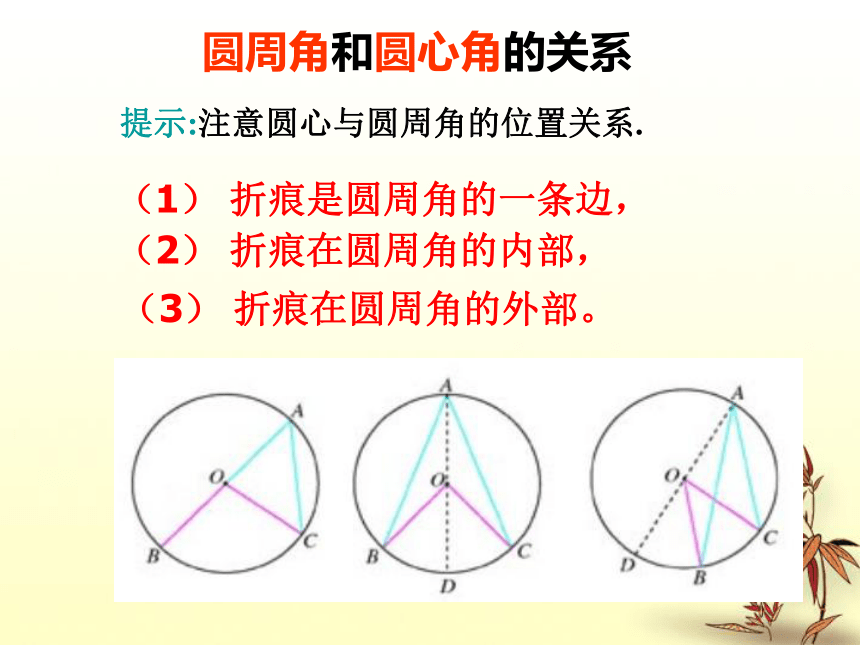
课件24张PPT。24.1 圆周角一、复习旧知:请说说我们是如何给圆心角下定义的,试回答?顶点在圆心的角叫圆心角。顶点在圆上,并且两边都和圆相交的角叫做圆周角. 1辩一辩 图中的∠CDE是圆周角吗?E二新授课圆周角和圆心角的关系 提示:注意圆心与圆周角的位置关系.(1) 折痕是圆周角的一条边, (2) 折痕在圆周角的内部, (3) 折痕在圆周角的外部。 分三种情况来证明:
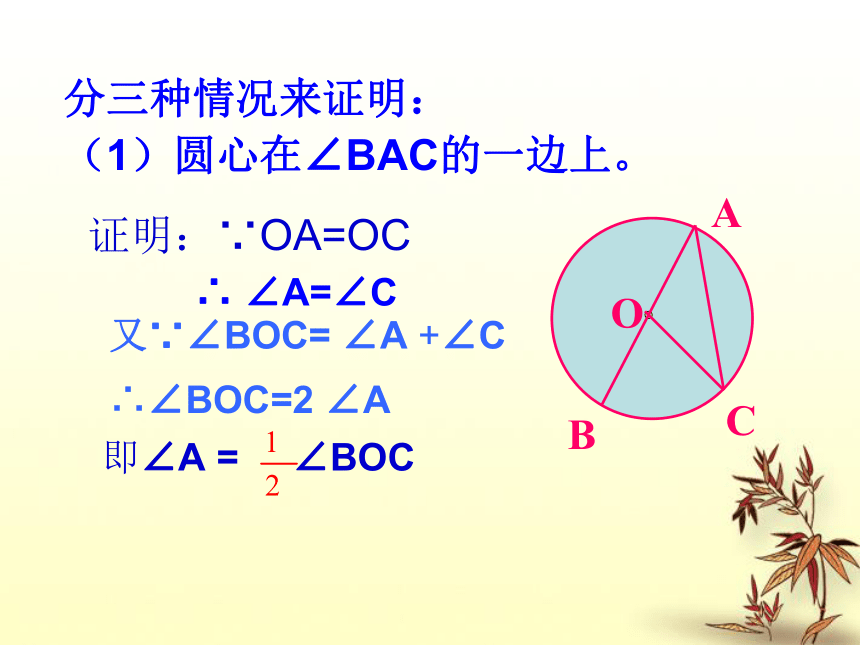
(1)圆心在∠BAC的一边上。
∴ ∠A=∠C证明:∵OA=OC又∵∠BOC= ∠A +∠C
∴∠BOC=2 ∠A
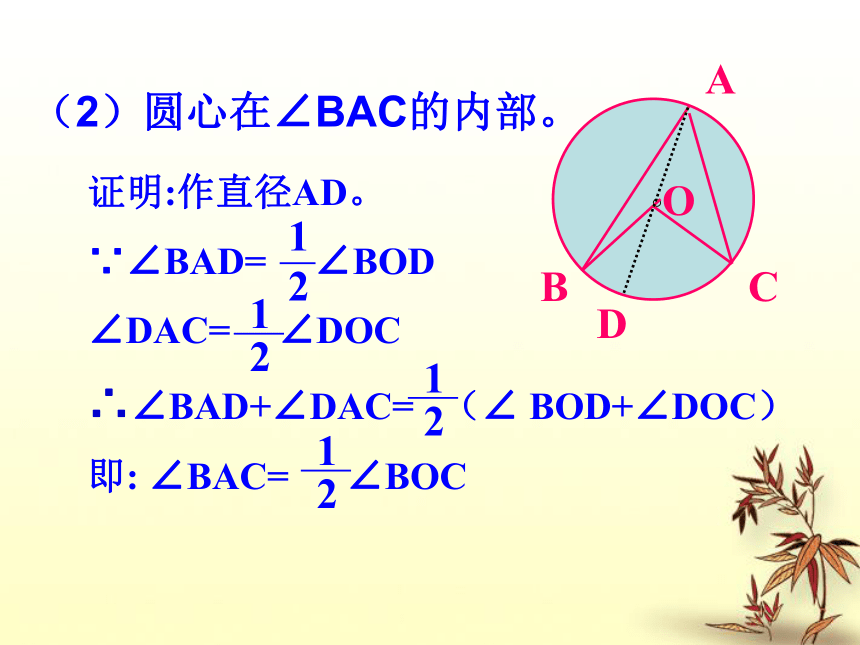
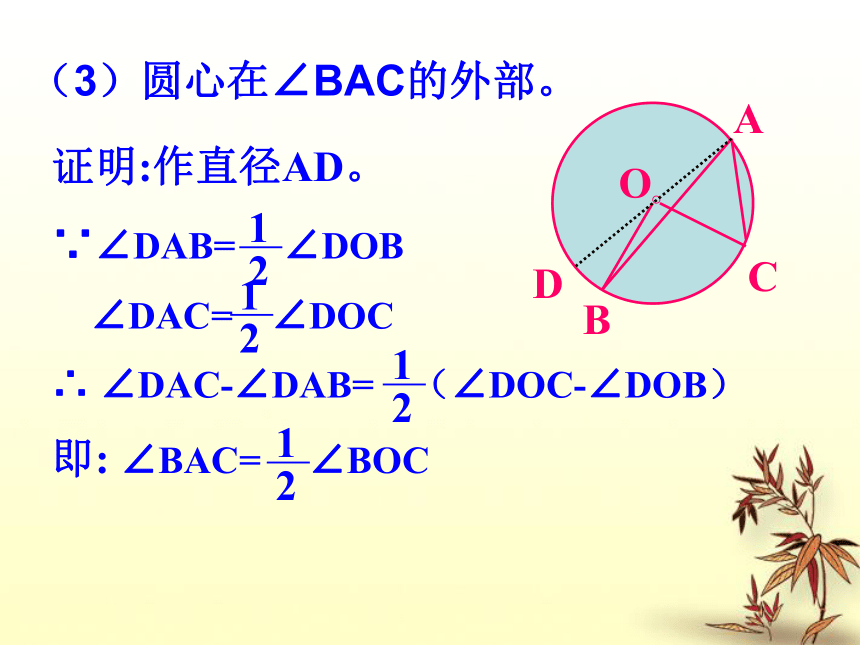
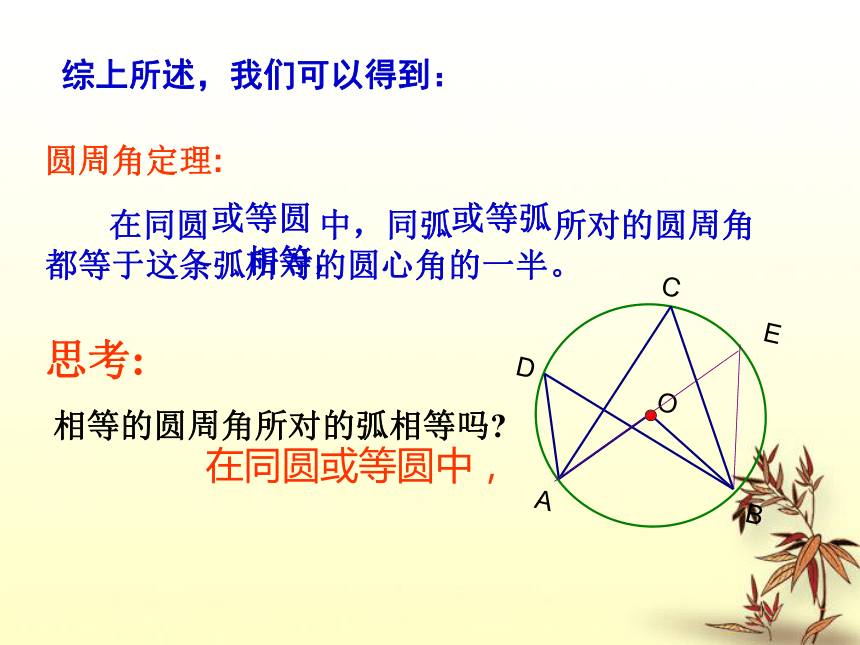
即∠A = ∠BOC(2)圆心在∠BAC的内部。(3)圆心在∠BAC的外部。D 综上所述,我们可以得到:圆周角定理: 在同圆 中,同弧 所对的圆周角 都等于这条弧所对的圆心角的一半。 或等圆或等弧相等,思考:
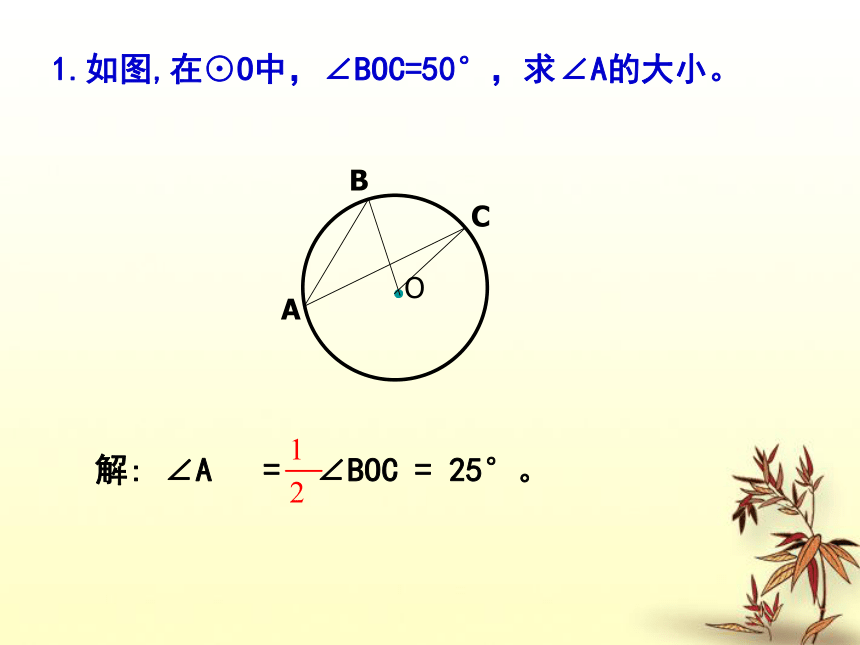
相等的圆周角所对的弧相等吗?在同圆或等圆中,1.如图,在⊙O中,∠BOC=50°,求∠A的大小。2.如图,∠A是圆O的圆周角,
∠A=40°,求∠OBC的度数。 3.试找出下图中所有相等的圆周角。 ∠2=∠7∠1=∠4∠3=∠6∠5=∠8探索如图,线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B),那么,∠ACB就是直径AB所对的圆周角,想想看,∠ACB会是怎样的角?思考
90°的圆周角所对的弦是什么? 从而得出结论:
90°的圆周角所对的弦是直径半圆(或直径)所对的圆周角是直角4.如图,在△ABC中,AB=AC=6,以AB为直径的半圆交BC于D,交AC于E,若∠DAC=30°,则∠BAC=___,BD=___。5, 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.又在Rt△ABD中,AD2+BD2=AB2,解:∵AB是直径,∴ ∠ACB= ∠ADB=90°.在Rt△ABC中,∵CD平分∠ACB,∴AD=BD.6,求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)·ABCO求证: △ABC 为直角三角形.证明:以AB为直径作⊙O,∵AO=BO, ∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴ △ABC 为直角三角形.(三)圆内接多边形与多边形的内接圆1.圆内接多边形与多边形的内接圆的定义
如何区别两个定义?(前者是特殊的多边形后者是特殊的圆)
2.圆内接四边形性质
这条性质的题设和结论分别是什么?怎样证明 课堂训练: 2. 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?请证明.7.如图,OA⊥BC,∠AOB=50°,试确定∠ADC的大小?8.如图,你能设法确定一个圆形纸片的圆心吗?你有多少种方法?与同学交流一下.DOOO·方法一方法二方法三方法四AB1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角。2.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。小结:1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角。2.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角。2.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。4. 圆内接多边形与多边形的内接圆概念和圆内接四边形性质 3. 半圆或直径所对的圆周角是直角, 90°的圆周角所对的弦是直径。
2.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。3. 应用本节定理解决相关问题.画一个圆心角,然后再画同弧所对的圆周角。量一量它们之间有什么大小关系?你发现了什么?有什么猜想?猜想: 同弧所对的圆周角等于它所对圆心角的一半。
作业1阅读作业:阅读教科书90至93页的内容
2巩固作业:教科书94页
习题24.1第2、3、4、5题
这节课你还有什么收获和体会,和大家一起分享一下吧!
(1)圆心在∠BAC的一边上。
∴ ∠A=∠C证明:∵OA=OC又∵∠BOC= ∠A +∠C
∴∠BOC=2 ∠A
即∠A = ∠BOC(2)圆心在∠BAC的内部。(3)圆心在∠BAC的外部。D 综上所述,我们可以得到:圆周角定理: 在同圆 中,同弧 所对的圆周角 都等于这条弧所对的圆心角的一半。 或等圆或等弧相等,思考:
相等的圆周角所对的弧相等吗?在同圆或等圆中,1.如图,在⊙O中,∠BOC=50°,求∠A的大小。2.如图,∠A是圆O的圆周角,
∠A=40°,求∠OBC的度数。 3.试找出下图中所有相等的圆周角。 ∠2=∠7∠1=∠4∠3=∠6∠5=∠8探索如图,线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B),那么,∠ACB就是直径AB所对的圆周角,想想看,∠ACB会是怎样的角?思考
90°的圆周角所对的弦是什么? 从而得出结论:
90°的圆周角所对的弦是直径半圆(或直径)所对的圆周角是直角4.如图,在△ABC中,AB=AC=6,以AB为直径的半圆交BC于D,交AC于E,若∠DAC=30°,则∠BAC=___,BD=___。5, 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.又在Rt△ABD中,AD2+BD2=AB2,解:∵AB是直径,∴ ∠ACB= ∠ADB=90°.在Rt△ABC中,∵CD平分∠ACB,∴AD=BD.6,求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)·ABCO求证: △ABC 为直角三角形.证明:以AB为直径作⊙O,∵AO=BO, ∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴ △ABC 为直角三角形.(三)圆内接多边形与多边形的内接圆1.圆内接多边形与多边形的内接圆的定义
如何区别两个定义?(前者是特殊的多边形后者是特殊的圆)
2.圆内接四边形性质
这条性质的题设和结论分别是什么?怎样证明 课堂训练: 2. 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?请证明.7.如图,OA⊥BC,∠AOB=50°,试确定∠ADC的大小?8.如图,你能设法确定一个圆形纸片的圆心吗?你有多少种方法?与同学交流一下.DOOO·方法一方法二方法三方法四AB1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角。2.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。小结:1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角。2.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角。2.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。4. 圆内接多边形与多边形的内接圆概念和圆内接四边形性质 3. 半圆或直径所对的圆周角是直角, 90°的圆周角所对的弦是直径。
2.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。3. 应用本节定理解决相关问题.画一个圆心角,然后再画同弧所对的圆周角。量一量它们之间有什么大小关系?你发现了什么?有什么猜想?猜想: 同弧所对的圆周角等于它所对圆心角的一半。
作业1阅读作业:阅读教科书90至93页的内容
2巩固作业:教科书94页
习题24.1第2、3、4、5题
这节课你还有什么收获和体会,和大家一起分享一下吧!
同课章节目录
