6.3.2实数课件(共42张PPT)
图片预览










文档简介
课件42张PPT。实 数人教版七年级数学下册
第六章6.3.2学习目标:
会求实数的相反数与绝对值,会对实数进行简单的运算.
学习重点:
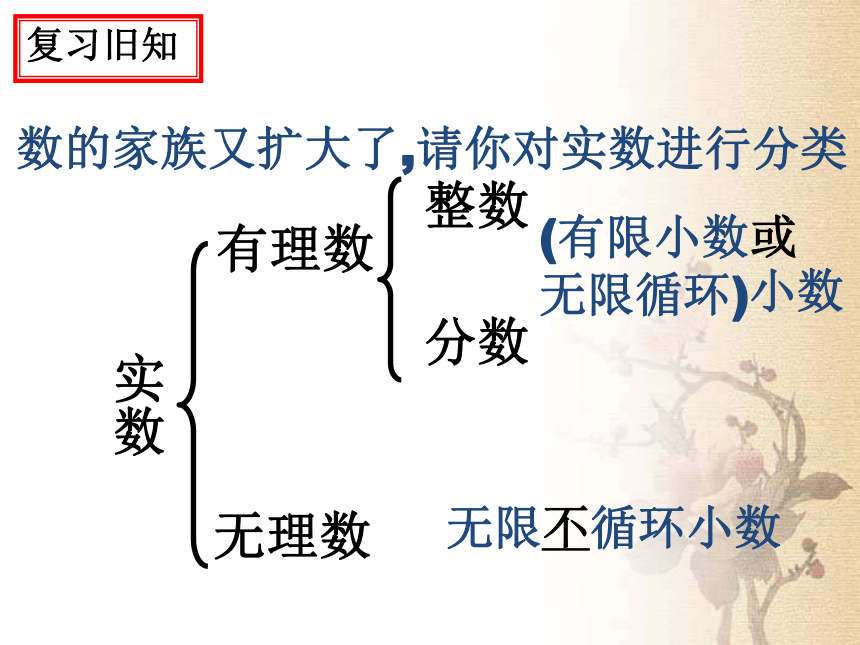
知道有理数的运算律和运算性质同样适合于实数的运算,并会进行简单的运算.课件说明数的家族又扩大了,请你对实数进行分类实数有理数无理数整数分数(有限小数或
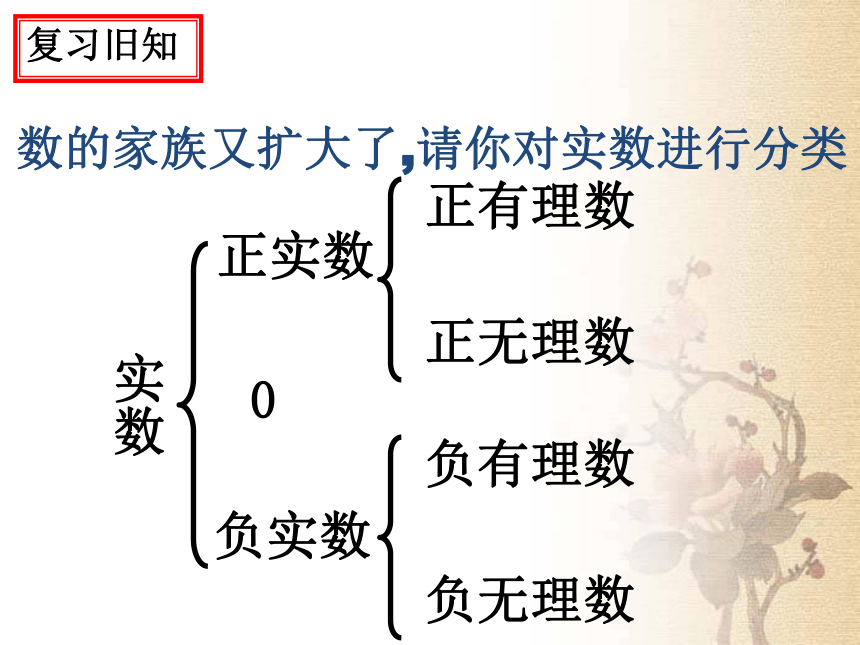
无限循环)无限不循环小数小数复习旧知实数正实数负实数正有理数0正无理数负有理数负无理数数的家族又扩大了,请你对实数进行分类复习旧知复习引入有理数关于相反数和绝对值的意义是什么?数 的相反数是 ,一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
0的绝对值是0.创设情境,引入新课1.求下列有理数的相反数、绝对值和倒数. 相反数:绝对值:倒 数:你能解答下列问题吗? (1) 的相反数是 ,
的相反数是 ,
0 的相反数是 ;
(2) = , = ,
= .探究新知 在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。它本身0它的相反数实数范围内的相反数、绝对值 的相反数是___________,
的相反数是__________,
0的相反数是__________.2. 00实数范围内的相反数、绝对值它本身它的相反数字母
表示3.求下列各数的相反数、倒数、绝对值: 例1
(1)分别写出 的相反数;
(2)指出 是什么数的相反数;
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.运用新知解:
(1) 的相反数是 ;
的相反数是 .
(2) 的相反数是 ;
的相反数是 .
(3) 的绝对值是4.
(4) 绝对值是 的数是 或 .运用新知1. 的相反数是 ,
的相反数是2. 5、在实数 中,
整数有
有理数有
无理数有
实数有它本身0它的相反数DD创设情境,引入新课2. 用字母表示有理数的加法交换律和结合律.
有理数的加法交换律:结合律:创设情境,引入新课3. 用字母表示有理数的乘法
交换律、乘法结合律、乘法分
配律.有理数的乘法交换律: 结合律:
分配律:实数范围内的简单计算例2:计算下列各式的值. (2)实数范围内的简单计算例2:计算下列各式的值. (2)
计算: (2) 实数范围内的简单计算例3:计算.(结果保留小数点后两位) (2)实数的运算顺序(1) 先算乘方和开方;
(2)再算乘除,最后算加;
(3)如果遇到括号, 则先进行括号里的运算引入合并算术平方根性质乘法交换律
结合律范例例1、计算下列各式的值:注意:(1)计算题解题格式;(2)根指数、被开方数都分别相
同的无理数要合并。巩固1、计算:(1)(2)范例例2、计算:(2)注意:(1)先去括号、绝对值;(2)再合并。巩固2、计算:(1)(2)探究 例3、计算:(1) (精确到0.01)(2) (结果保留3个有效数字)注意:(1)无理数近似值多取1位;(2)结果按要求取近似值。巩固 3、计算:(1) (精确到0.01)(2) (保留3个有效数字)范例例4、解方程:(1)(2)注意:(1)将括号看作一个整体;(2)开平方有两个值,开立方只有一个值。(3)巩固5、解方程:(1)(2)(3)2、(结果保留3个有效数字)注意:计算过程中要多保留一位!解:(3)原式=
=18.94≈18.9一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.两个无理数之积不一定是无理数。( )7.两个无理数之和一定是无理数。( )×××课后作业教材习题6.3第3、4、5题.比一比8算一算( )651.绝对值等于它本身的实数只有0.2.倒数等于它本身的实数只有1.3.相反数等于它本身的实数只有0.4.算术平方根等于本身的实数只有1.5.有算术平方根的数是有理数.辩一辩6.0是最小的实数.7.无限小数都是无理数.9.带根号的数都是无理数. 10.不带根号的数都是有理数.8.无理数都是无限小数.归纳总结什么是实数的相反数和绝对值? 举例说明.布置作业教科书 第56页练习第3题,
习题6.3 第3、4、5题再 见
第六章6.3.2学习目标:
会求实数的相反数与绝对值,会对实数进行简单的运算.
学习重点:
知道有理数的运算律和运算性质同样适合于实数的运算,并会进行简单的运算.课件说明数的家族又扩大了,请你对实数进行分类实数有理数无理数整数分数(有限小数或
无限循环)无限不循环小数小数复习旧知实数正实数负实数正有理数0正无理数负有理数负无理数数的家族又扩大了,请你对实数进行分类复习旧知复习引入有理数关于相反数和绝对值的意义是什么?数 的相反数是 ,一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
0的绝对值是0.创设情境,引入新课1.求下列有理数的相反数、绝对值和倒数. 相反数:绝对值:倒 数:你能解答下列问题吗? (1) 的相反数是 ,
的相反数是 ,
0 的相反数是 ;
(2) = , = ,
= .探究新知 在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。它本身0它的相反数实数范围内的相反数、绝对值 的相反数是___________,
的相反数是__________,
0的相反数是__________.2. 00实数范围内的相反数、绝对值它本身它的相反数字母
表示3.求下列各数的相反数、倒数、绝对值: 例1
(1)分别写出 的相反数;
(2)指出 是什么数的相反数;
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.运用新知解:
(1) 的相反数是 ;
的相反数是 .
(2) 的相反数是 ;
的相反数是 .
(3) 的绝对值是4.
(4) 绝对值是 的数是 或 .运用新知1. 的相反数是 ,
的相反数是2. 5、在实数 中,
整数有
有理数有
无理数有
实数有它本身0它的相反数DD创设情境,引入新课2. 用字母表示有理数的加法交换律和结合律.
有理数的加法交换律:结合律:创设情境,引入新课3. 用字母表示有理数的乘法
交换律、乘法结合律、乘法分
配律.有理数的乘法交换律: 结合律:
分配律:实数范围内的简单计算例2:计算下列各式的值. (2)实数范围内的简单计算例2:计算下列各式的值. (2)
计算: (2) 实数范围内的简单计算例3:计算.(结果保留小数点后两位) (2)实数的运算顺序(1) 先算乘方和开方;
(2)再算乘除,最后算加;
(3)如果遇到括号, 则先进行括号里的运算引入合并算术平方根性质乘法交换律
结合律范例例1、计算下列各式的值:注意:(1)计算题解题格式;(2)根指数、被开方数都分别相
同的无理数要合并。巩固1、计算:(1)(2)范例例2、计算:(2)注意:(1)先去括号、绝对值;(2)再合并。巩固2、计算:(1)(2)探究 例3、计算:(1) (精确到0.01)(2) (结果保留3个有效数字)注意:(1)无理数近似值多取1位;(2)结果按要求取近似值。巩固 3、计算:(1) (精确到0.01)(2) (保留3个有效数字)范例例4、解方程:(1)(2)注意:(1)将括号看作一个整体;(2)开平方有两个值,开立方只有一个值。(3)巩固5、解方程:(1)(2)(3)2、(结果保留3个有效数字)注意:计算过程中要多保留一位!解:(3)原式=
=18.94≈18.9一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.两个无理数之积不一定是无理数。( )7.两个无理数之和一定是无理数。( )×××课后作业教材习题6.3第3、4、5题.比一比8算一算( )651.绝对值等于它本身的实数只有0.2.倒数等于它本身的实数只有1.3.相反数等于它本身的实数只有0.4.算术平方根等于本身的实数只有1.5.有算术平方根的数是有理数.辩一辩6.0是最小的实数.7.无限小数都是无理数.9.带根号的数都是无理数. 10.不带根号的数都是有理数.8.无理数都是无限小数.归纳总结什么是实数的相反数和绝对值? 举例说明.布置作业教科书 第56页练习第3题,
习题6.3 第3、4、5题再 见
