人教版数学七年级上册第四章几何图形初步—线段的计算热点归纳(含答案)
文档属性
| 名称 | 人教版数学七年级上册第四章几何图形初步—线段的计算热点归纳(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 303.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-08 00:00:00 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
线段的计算热点题型归纳
一、直接计算
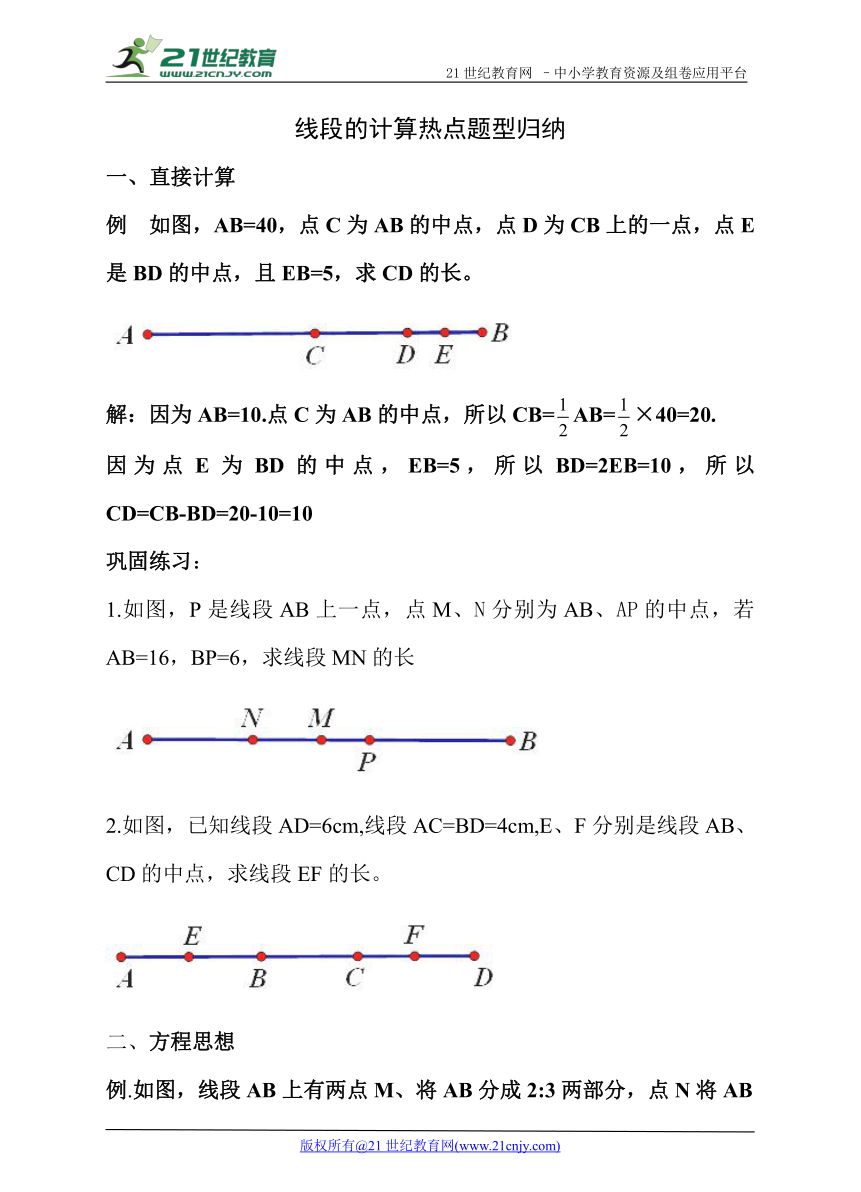
例 如图,AB=40,点C为AB的中点,点D为CB上的一点,点E是BD的中点,且EB=5,求CD的长。21·cn·jy·com
( http: / / www.21cnjy.com )
解:因为AB=10.点C为AB的中点,所以CB=AB=×40=20.
因为点E为BD的中点,EB=5,所以BD=2EB=10,所以CD=CB-BD=20-10=10
巩固练习:
1.如图,P是线段AB上一点,点M、N分别为AB、AP的中点,若AB=16,BP=6,求线段MN的长www.21-cn-jy.com
( http: / / www.21cnjy.com )
2.如图,已知线段AD=6cm,线段AC=BD=4cm,E、F分别是线段AB、CD的中点,求线段EF的长。2·1·c·n·j·y
( http: / / www.21cnjy.com )
二、方程思想
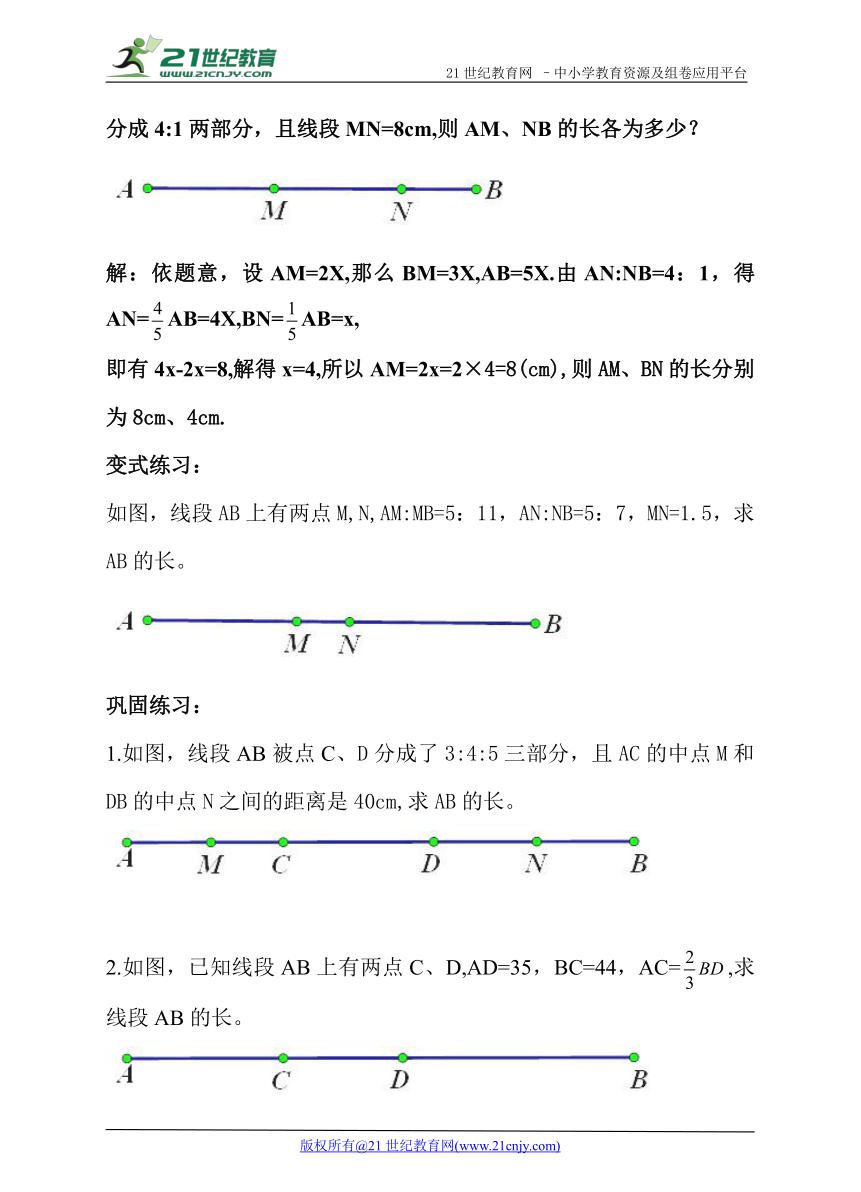
例.如图,线段AB上有两点M、将AB分成2:3两部分,点N将AB分成4:1两部分,且线段MN=8cm,则AM、NB的长各为多少?
( http: / / www.21cnjy.com )
解:依题意,设AM=2X,那么BM=3X,AB=5X.由AN:NB=4:1,得AN=AB=4X,BN=AB=x,【来源:21·世纪·教育·网】
即有4x-2x=8,解得x=4,所以AM=2x=2×4=8(cm),则AM、BN的长分别为8cm、4cm.2-1-c-n-j-y
变式练习:
如图,线段AB上有两点M,N,AM:MB=5:11,AN:NB=5:7,MN=1.5,求AB的长。
( http: / / www.21cnjy.com )
巩固练习:
1.如图,线段AB被点C、D分成了3:4:5三部分,且AC的中点M和DB的中点N之间的距离是40cm,求AB的长。www-2-1-cnjy-com
( http: / / www.21cnjy.com )
2.如图,已知线段AB上有两点C、D,AD=35,BC=44,AC=,求线段AB的长。
( http: / / www.21cnjy.com )
三、分类讨论的思想
例 已知线段AB=14cm,在直线AB上有一点C,且BC=4cm,,M是线段AC的中点,求线段AM的长。21教育网
解:(1)当点C在线段AB上时
( http: / / www.21cnjy.com )
因为M是线段AC的中点,所以AM=AC,又因为C=AB-BC,AB=14cm,BC=4cm,所以AM=(AB-AC)= (14-4)=5cm.
(2)当点C在线段AB的延长线上时,如图
( http: / / www.21cnjy.com )
因为M是线段AC的中点,所以AM=AC,又因为AC=AB+C,AB=14cm,BC=4cm,所以AM=(AB+C)= (14+4)=9cm.
变式练习
已知线段AB、BC在同一直线上,AB=5,BC=2,求AC的长。
巩固练习
1.已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,求线段MN的长。21·世纪*教育网
2.知线段AB=12,在AB上有C、D、M、N四个点,且AC:CD:DB=1:2:3,AM=AC,DN=BD,求线段MN的长。21世纪教育网版权所有
四、整体思想
例 如图,已知点C、D为线段AB上顺次两点,M、N分别为AC、BD的中点。
(1)若AB=24,CD=10,求MN的长,
(2)若AB=a,CD=b,试用含有a,b的代数式表示M、N的长。
( http: / / www.21cnjy.com )
解:(1)∵AB=24,CD=10,
∴AC+DB=AB-CD=14
∴(AC+DB)=MC+DN=7
∴MN=MC+DN+CD=17
(2) 若AB=a,CD=b,则AC+DB=a-b
∴MC+DN=(AC+DB)= (a-b)
∴MN=MC+DN+CD=(a-b)+b=(a-b)
巩固练习
如图,点C在线段AB上,点M、N分别是AC、BC的中点,且AB=a cm
(1)若C为线段AB上任一点,你能猜想出MN的长度吗?说明理由;
(2)若C在线段AB的延长线上,你能猜想MN的长度吗?请画出图形,写出结论,并说明理由。
(3)你能用简洁的话,描述你发现的结论吗?
( http: / / www.21cnjy.com )
参考答案
一、巩固练习1.MN=3 2.EF=4cm
二、变式练习AB=14.4
巩固练习1.AB=60cm
2.AB=62
三、变式练习7或者3
巩固练习1.当点C在线段AB上时MN=5;当点C在AB延长线上时,MN=5
2.当点N在点D右侧时,MN=6.5;当点N在点D左侧时,MN=3.5
四、巩固练习
(1)MN=a
(2)图略MN=a
(3)只要满足点C在线段AB所在的直线上,点M、N分别是AC、BC的中点,那么MN就等于AB的一半。21cnjy.com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
线段的计算热点题型归纳
一、直接计算
例 如图,AB=40,点C为AB的中点,点D为CB上的一点,点E是BD的中点,且EB=5,求CD的长。21·cn·jy·com
( http: / / www.21cnjy.com )
解:因为AB=10.点C为AB的中点,所以CB=AB=×40=20.
因为点E为BD的中点,EB=5,所以BD=2EB=10,所以CD=CB-BD=20-10=10
巩固练习:
1.如图,P是线段AB上一点,点M、N分别为AB、AP的中点,若AB=16,BP=6,求线段MN的长www.21-cn-jy.com
( http: / / www.21cnjy.com )
2.如图,已知线段AD=6cm,线段AC=BD=4cm,E、F分别是线段AB、CD的中点,求线段EF的长。2·1·c·n·j·y
( http: / / www.21cnjy.com )
二、方程思想
例.如图,线段AB上有两点M、将AB分成2:3两部分,点N将AB分成4:1两部分,且线段MN=8cm,则AM、NB的长各为多少?
( http: / / www.21cnjy.com )
解:依题意,设AM=2X,那么BM=3X,AB=5X.由AN:NB=4:1,得AN=AB=4X,BN=AB=x,【来源:21·世纪·教育·网】
即有4x-2x=8,解得x=4,所以AM=2x=2×4=8(cm),则AM、BN的长分别为8cm、4cm.2-1-c-n-j-y
变式练习:
如图,线段AB上有两点M,N,AM:MB=5:11,AN:NB=5:7,MN=1.5,求AB的长。
( http: / / www.21cnjy.com )
巩固练习:
1.如图,线段AB被点C、D分成了3:4:5三部分,且AC的中点M和DB的中点N之间的距离是40cm,求AB的长。www-2-1-cnjy-com
( http: / / www.21cnjy.com )
2.如图,已知线段AB上有两点C、D,AD=35,BC=44,AC=,求线段AB的长。
( http: / / www.21cnjy.com )
三、分类讨论的思想
例 已知线段AB=14cm,在直线AB上有一点C,且BC=4cm,,M是线段AC的中点,求线段AM的长。21教育网
解:(1)当点C在线段AB上时
( http: / / www.21cnjy.com )
因为M是线段AC的中点,所以AM=AC,又因为C=AB-BC,AB=14cm,BC=4cm,所以AM=(AB-AC)= (14-4)=5cm.
(2)当点C在线段AB的延长线上时,如图
( http: / / www.21cnjy.com )
因为M是线段AC的中点,所以AM=AC,又因为AC=AB+C,AB=14cm,BC=4cm,所以AM=(AB+C)= (14+4)=9cm.
变式练习
已知线段AB、BC在同一直线上,AB=5,BC=2,求AC的长。
巩固练习
1.已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,求线段MN的长。21·世纪*教育网
2.知线段AB=12,在AB上有C、D、M、N四个点,且AC:CD:DB=1:2:3,AM=AC,DN=BD,求线段MN的长。21世纪教育网版权所有
四、整体思想
例 如图,已知点C、D为线段AB上顺次两点,M、N分别为AC、BD的中点。
(1)若AB=24,CD=10,求MN的长,
(2)若AB=a,CD=b,试用含有a,b的代数式表示M、N的长。
( http: / / www.21cnjy.com )
解:(1)∵AB=24,CD=10,
∴AC+DB=AB-CD=14
∴(AC+DB)=MC+DN=7
∴MN=MC+DN+CD=17
(2) 若AB=a,CD=b,则AC+DB=a-b
∴MC+DN=(AC+DB)= (a-b)
∴MN=MC+DN+CD=(a-b)+b=(a-b)
巩固练习
如图,点C在线段AB上,点M、N分别是AC、BC的中点,且AB=a cm
(1)若C为线段AB上任一点,你能猜想出MN的长度吗?说明理由;
(2)若C在线段AB的延长线上,你能猜想MN的长度吗?请画出图形,写出结论,并说明理由。
(3)你能用简洁的话,描述你发现的结论吗?
( http: / / www.21cnjy.com )
参考答案
一、巩固练习1.MN=3 2.EF=4cm
二、变式练习AB=14.4
巩固练习1.AB=60cm
2.AB=62
三、变式练习7或者3
巩固练习1.当点C在线段AB上时MN=5;当点C在AB延长线上时,MN=5
2.当点N在点D右侧时,MN=6.5;当点N在点D左侧时,MN=3.5
四、巩固练习
(1)MN=a
(2)图略MN=a
(3)只要满足点C在线段AB所在的直线上,点M、N分别是AC、BC的中点,那么MN就等于AB的一半。21cnjy.com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
