1.3直角三角形全等的判定 同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
1.3直角三角形全等的判定练习题
一、选择题
1. 在△ABC中，a、b、c分别为∠A、∠B、∠C的对边，则下列条件中：①a=10,b=8,c=6;②a2=3,b2=4,c2=5;③a2=(b+c)(b-c)；④∠A=2∠B=2∠C。其中能判断△ABC是直角三角形的有（ ）www.21-cn-jy.com
A、1个 B、2个 C、3个 D、4个
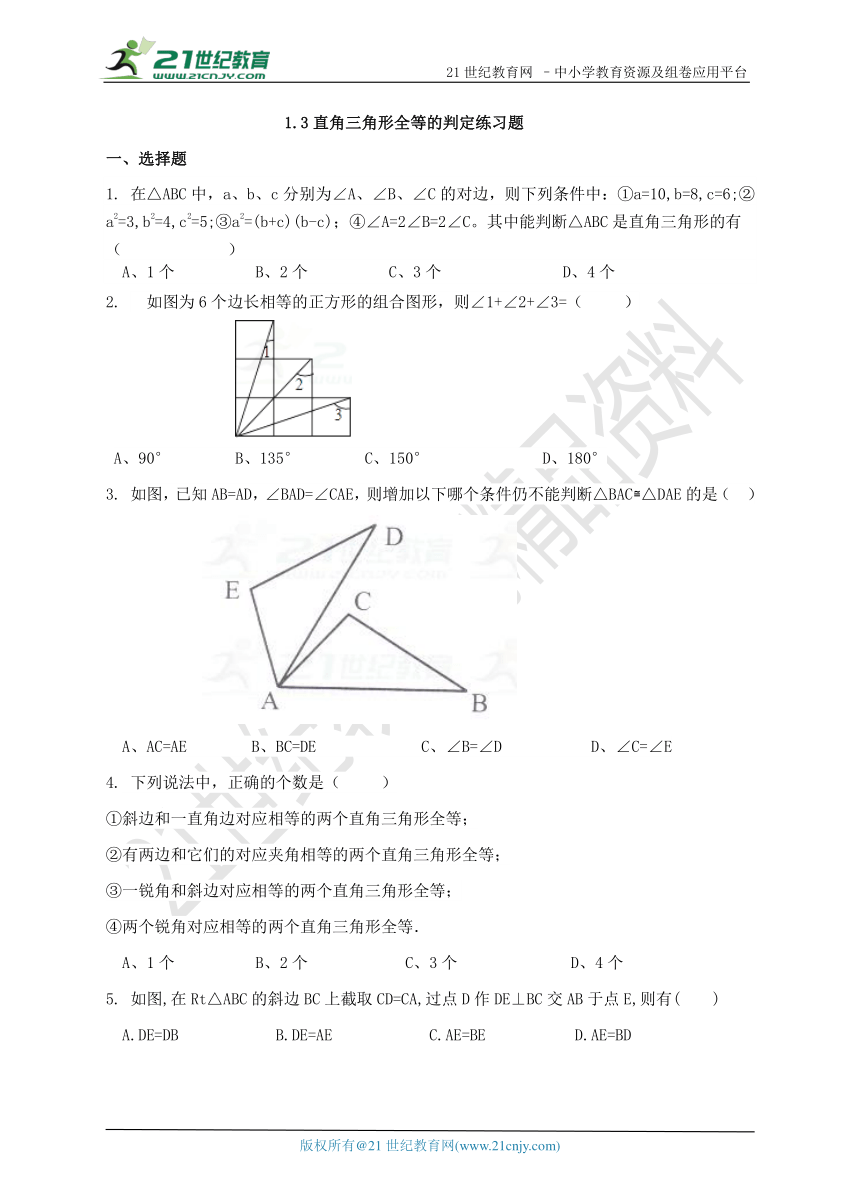
2. 如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=（ ）
A、90° B、135° C、150° D、180°
3. 如图，已知AB=AD，∠BAD=∠CAE，则增加以下哪个条件仍不能判断△BAC △DAE的是（ ）
A、AC=AE B、BC=DE C、∠B=∠D D、∠C=∠E
4. 下列说法中，正确的个数是（ ）
①斜边和一直角边对应相等的两个直角三角形全等；
②有两边和它们的对应夹角相等的两个直角三角形全等；
③一锐角和斜边对应相等的两个直角三角形全等；
④两个锐角对应相等的两个直角三角形全等．2·1·c·n·j·y
A、1个 B、2个 C、3个 D、4个
5. 如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )
A.DE=DB B.DE=AE C.AE=BE D.AE=BD
6. 如图，南京路与八一街垂直，西安路也与八一街垂直，曙光路与环城路垂直．如果小明站在南京路与八一街的交叉口，准备去书店，按图中的街道行走，最近的路程为( )m.【来源：21·世纪·教育·网】
A.400 B.600 C.500 D.700
二、填空题
7. 已知一条斜边和一条直角边，求作直角三角形，作图的依据是__________.
8. 如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点F，若BF=AC，
则∠ABC= 度．
9. 如图所示，已知BE⊥AD，CF⊥AD，垂足分别为E，F，则在下列条件中选择一组，可以判定 Rt△ABE≌Rt△DCF的是 （填入序号） 21·世纪*教育网
①AB=DC，∠B=∠C； ②AB=DC，AB∥CD；
③AB=DC，BE=CF； ④AB=DF，BE=CF．www-2-1-cnjy-com
10．如图，有一个直角三角形ABC，∠C=90°，AC=10，BC=5，一条线段PQ=AB，P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动，问P点运动到 位置时，才能使ΔABC≌ΔPQA. 2-1-c-n-j-y
三、解答题
11. 如图，在△ABC中，已知D是BC中点，DE⊥AB，DF⊥AC，垂足分别是E、F，DE＝DF. 求证：AB=AC21*cnjy*com
12. 已知：如图，AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC＝DC.你能说明BE与DF相等吗？【来源：21cnj*y.co*m】
13. 已知如图，AC⊥BC，AD⊥BD，AD=BC，CE⊥AB，DF⊥AB，垂足分别是E、F
求证：CE=DF.
14. 已知：Rt△ABC中，∠ACB是直角，D是AB上一点，BD=BC，过D作AB的垂线交AC于E，求证：CD⊥BE【出处：21教育名师】
15.如图，在△ABC中，AB=AC，DE是过点A的直线，BD⊥DE于D，CE⊥DE于点E；
（1）若B、C在DE的同侧（如图所示）且AD=CE．求证：AB⊥AC；【版权所有：21教育】
（2）若B、C在DE的两侧（如图所示），其他条件不变，AB与AC仍垂直吗？若是请给出证明；若不是，请说明理由．21教育名师原创作品
答案：
1.C
2. B
3. B
4.C
5. B
分析：连接EC,可证明△ACE≌△DCE,从而得到答案。
解：连接EC,∵CD=CA，EC=EC，∴△ACE≌△DCE ，故得到DE=AE ，选B。
6. C
分析：由于BC∥AD，那么有∠DAE=∠ACB，由题意可知∠ABC=∠DEA=90°，BA=ED，利用AAS可证△ABC≌△DEA，于是AE=BC=300，再利用勾股定理可求AC，即可求CE，根据图可知从B到E的走法有两种，分别计算比较即可．
解：如右图所示，
∵BC∥AD，
∴∠DAE=∠ACB，
又∵BC⊥AB，DE⊥AC，
∴∠ABC=∠DEA=90°，
又∵AB=DE=400m，
∴△ABC≌△DEA，
∴EA=BC=300m，
在Rt△ABC中，AC=500m，
∴CE=AC-AE=200，
从B到E有两种走法：①BA+AE=700m；②BC+CE=500m，
∴最近的路程是500m．故答案为500m。故选C。
7.分析：
结论：如图所示，Rt△ABC即为所求作的三角形．
解：HL
8. 45
9. ①②③
10．AC中点或C点
解：点P运动到AC中点时，△ABC≌△QPA．
∵AX⊥AC，∠C=90°，
∴∠C=∠PAQ=90°，
又∵AP=CB=5，PQ=AB，
∴△ABC≌△QPA．
点P运动到C点时，△ABC≌△QPA．
∵AX⊥AC，∠C=90°，
∴∠BCA=∠PAQ=90°，
又∵AP=CA=10，PQ=AB，
∴△ABC≌△QPA．21世纪教育网版权所有
11.
证明：
∵D是BC的中点，
∴BD=CD，
∵DE⊥AB，DF⊥AC，
在Rt△BED和Rt△CFD中，
BD=CDBE=CF
∴Rt△BED≌Rt△CFD（HL），
∴∠B=∠C，
∴AB=AC，
又∵D为BC的中点，
∴AD⊥BC（三线合一）．21教育网
12.
证明：∵AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，
∴∠CFD=90°，∠CEB=90°（垂线的意义）
CE=CF（角平分线的性质）
∵BC=CD（已知）
∴Rt△BCE≌Rt△DCF（HL）21cnjy.com
∴BE=DF
13.
证明：在Rt△ACB与Rt△ABD中
∴Rt△ACB≌Rt△BDF（HL）
∴∠CAB=∠DBA，AC=BD
∴在Rt△CAE与Rt△BDF中
∴△CAE≌△BDF（AAS）
∴CE=DF.
14.
证明：∵DE⊥AB∴∠BDE=90°，∵∠ACB=90°
∴在Rt△DEB中与Rt△CEB中
BD=BC
BE=BE
∴Rt△DEB≌Rt△CEB（HL）
∴DE=EC
又∵BD=BC
∴E、B在CD的垂直平分线上
即BE⊥CD.
15. 解：（1）证明：∵BD⊥DE，CE⊥DE，
∴∠ADB=∠AEC=90°，
在Rt△ABD和Rt△ACE中，
∵，
∴Rt△ABD≌Rt△ACE．
∴∠DAB=∠EAC，∠DBA=∠ACE．
∵∠DAB+∠DBA=90°，∠EAC+∠ACE=90°，
∴∠BAD+∠CAE=90°．
∠BAC=180°﹣（∠BAD+∠CAE）=90°．
∴AB⊥AC．
（2）AB⊥AC．理由如下：
同（1）一样可证得Rt△ABD≌Rt△ACE．
∴∠DAB=∠ECA，∠DBA=∠EAC，
∵∠CAE+∠ECA=90°，
∴∠CAE+∠BAD=90°，即∠BAC=90°，
∴AB⊥AC．21·cn·jy·com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)