青岛版八年级上册第5章几何证明初步5.3 什么是几何证明 课件
文档属性
| 名称 | 青岛版八年级上册第5章几何证明初步5.3 什么是几何证明 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-08 00:00:00 | ||
图片预览






文档简介
课件16张PPT。◇祝各位老师:身体健康 万事如意。祝同学们:笑口常开 学业有成。巨野县大谢集镇一中 王传青5.3 什么是几何证明
1、了解基本事实、证明、定理的意义,掌握本节中提出的基本事实,了解除了基本事实外,命题的真实性必须经过证明;
2、初步了解证明的三个步骤,通过例题了解几何证明的书写格式,知道证明要合逻辑,感受证明过程中的每一步推理都要有依据。
你能根据阅读的课本内容完成下列填空吗?试试看。
1. 人们通过长期实践总结出来,被大家所公认的______作为基本事实,用基本事实作为证实所有其他几何命题的起始依据.
2.本书确定下列命题作为基本事实:
(1)两点确定一条______.
(2)两点之间,____最短.
(3)过一点有且只有_______与这条直线垂直.
(4)两条直线被第三条直线所截,如果同位角相等,那么两直线_____.
(5)过直线外一点有且只有一条直线与这条直线_____;
(6)两边及其夹角分别____________的两个三角形全等;
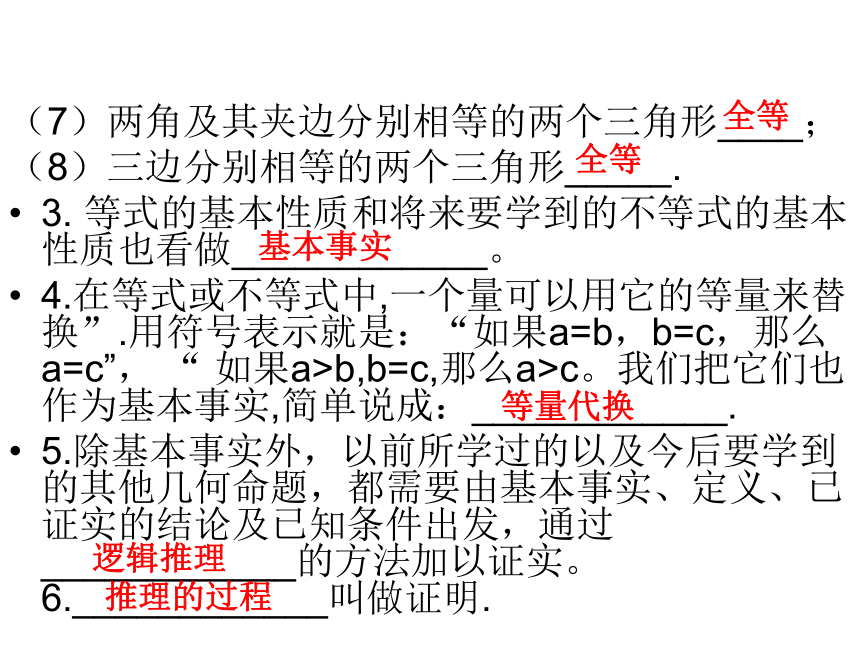
(7)两角及其夹边分别相等的两个三角形____;
(8)三边分别相等的两个三角形_____.
3. 等式的基本性质和将来要学到的不等式的基本性质也看做____________。
4.在等式或不等式中,一个量可以用它的等量来替换”.用符号表示就是:“如果a=b,b=c,那么a=c”, “ 如果a>b,b=c,那么a>c。我们把它们也作为基本事实,简单说成:____________.
5.除基本事实外,以前所学过的以及今后要学到的其他几何命题,都需要由基本事实、定义、已证实的结论及已知条件出发,通过____________的方法加以证实。____________叫做证明.1. 人们通过长期实践总结出来,被大家所公认的______作为基本事实,用基本事实作为证实所有其他几何命题的起始依据.
2.本书确定下列命题作为基本事实:
(1)两点确定一条______.
(2)两点之间,____最短.
(3)过一点有且只有_______与这条直线垂直.
(4)两条直线被第三条直线所截,如果同位角相等,那么两直线_____.
(5)过直线外一点有且只有一条直线与这条直线_____;
(6)两边及其夹角分别_______的两个三角形全等;命题直线线段一条直线平行相等平行
(7)两角及其夹边分别相等的两个三角形____;
(8)三边分别相等的两个三角形_____.
3. 等式的基本性质和将来要学到的不等式的基本性质也看做____________。
4.在等式或不等式中,一个量可以用它的等量来替换”.用符号表示就是:“如果a=b,b=c,那么a=c”, “ 如果a>b,b=c,那么a>c。我们把它们也作为基本事实,简单说成:____________.
5.除基本事实外,以前所学过的以及今后要学到的其他几何命题,都需要由基本事实、定义、已证实的结论及已知条件出发,通过____________的方法加以证实。6.____________叫做证明.
全等全等基本事实等量代换推理的过程逻辑推理1、“如果两个角是对顶角,那么这两个角相等”的条件是________________,结论是_________________。2、如图所示:证明:∵∠AOC与∠BOD是对顶角(已知)
∴∠AOC+∠AOD=180°,
∠AOD+∠BOD= 180(平角的定义)
∴∠AOC+∠AOD=∠AOD+∠BOD(等量代换)
∴∠AOC=∠BOD(等式的基本性质)
3、条件: ∠AOC与∠BOD是对顶角
结论:∠AOC=∠BOD
这两个角相等两个角是对顶角OCBAD 4、已知: ∠AOC与∠BOD是对顶角
求证:∠AOC=∠BOD
交流与探索活动一把经过推理得到证实的真命题叫做定理定理可以作为今后证明其他命题的依据。定理与定义和基本事实一样,具有普遍的意义。“如果两个角是对顶角,那么这两个角相等”称为对顶角的性质定理,简单说成:对顶角相等。活动二例1 求证:同角的余角相等
第一步:根据题意,画出图形.
先根据命题的条件即已知事项,画出图形,再根据命题
的结论的需要在图上标出必要的字母或符号,以便于叙述或
推理过程的表达.【归纳升华】第二步:结合图形,根据条件、结论,写出已知、求证.
把命题条件、结论中的文字语言转化为几何中的符号语言写在已知、求证中。
第三步:找出由已知推出求证的途径,写出“证明” .
证明过程应按照“前因后果”的次序书写,其中的每一步推理都要有依据,推理的依据只能是基本事实、已学过的定义、已经证明过的定理和已知条件,不能凭“想当然”。
证明的一般步骤巩固与练习求证:同角的补角相等(画出图形,写出已知、求证,证明)
四、小结反思:
小组内讨论交流,通过本节课的学习,你掌握了那些知识?还有那些疑问? 达标测试
一、选择题
1、“两点确定一条直线”这句话是( )
A、假命题 B、定义 C、基本事实 D、以上答案都不对
2、下列命题不是基本事实的是( )
A、两点确定一条直线
B、两直线平行,同位角相等
C、过直线外一点有且只有一条直线与这条直线平行;
D、同位角相等,两直线平行
CB二、填空题,
3、阅读并理解下列各题的证明过程,并在每步后的括号内填写该步推理的依据。
已知:如图,B,C是线段AD上的两点,且AB=CD。
求证:AC=BD.
证明:∵AB=CD( )
∴AB+BC=CD+BC( )
∴AC=BD( )线段和的定义等式的基本性质已知三、解答题
4、已知:如图,直线AB,CD相交于点O, 且∠AOC是直角。
求证:∠COB,∠BOD, ∠DOA都是直角。证明:∵ ∠AOC是直角(已知),
∴ ∠AOC= 90°( 直角的定义),
∵直线AB,CD相交于点O,(已知),
∴∠AOC+∠COB=180°(平角的定义),
∴ ∠COB=180°∠AOC= 90°(等式的基本性质),
∴ ∠COB是直角(直角的定义),
∵ ∠ AOC与∠ BOD是对顶角,∠COB于 ∠DOA是对顶角(已知),
∴ ∠ AOC=∠BOD, ∠COB= ∠DOA (对顶角的性质),
∴ ∠ BOD,∠DOA都是直角(等量代换)
∴ ∠COB, ∠BOD, ∠DOA都是直角
作业必做题:课本166页第2题、第3题
选做题:课本166页第4题再 见
1、了解基本事实、证明、定理的意义,掌握本节中提出的基本事实,了解除了基本事实外,命题的真实性必须经过证明;
2、初步了解证明的三个步骤,通过例题了解几何证明的书写格式,知道证明要合逻辑,感受证明过程中的每一步推理都要有依据。
你能根据阅读的课本内容完成下列填空吗?试试看。
1. 人们通过长期实践总结出来,被大家所公认的______作为基本事实,用基本事实作为证实所有其他几何命题的起始依据.
2.本书确定下列命题作为基本事实:
(1)两点确定一条______.
(2)两点之间,____最短.
(3)过一点有且只有_______与这条直线垂直.
(4)两条直线被第三条直线所截,如果同位角相等,那么两直线_____.
(5)过直线外一点有且只有一条直线与这条直线_____;
(6)两边及其夹角分别____________的两个三角形全等;
(7)两角及其夹边分别相等的两个三角形____;
(8)三边分别相等的两个三角形_____.
3. 等式的基本性质和将来要学到的不等式的基本性质也看做____________。
4.在等式或不等式中,一个量可以用它的等量来替换”.用符号表示就是:“如果a=b,b=c,那么a=c”, “ 如果a>b,b=c,那么a>c。我们把它们也作为基本事实,简单说成:____________.
5.除基本事实外,以前所学过的以及今后要学到的其他几何命题,都需要由基本事实、定义、已证实的结论及已知条件出发,通过____________的方法加以证实。____________叫做证明.1. 人们通过长期实践总结出来,被大家所公认的______作为基本事实,用基本事实作为证实所有其他几何命题的起始依据.
2.本书确定下列命题作为基本事实:
(1)两点确定一条______.
(2)两点之间,____最短.
(3)过一点有且只有_______与这条直线垂直.
(4)两条直线被第三条直线所截,如果同位角相等,那么两直线_____.
(5)过直线外一点有且只有一条直线与这条直线_____;
(6)两边及其夹角分别_______的两个三角形全等;命题直线线段一条直线平行相等平行
(7)两角及其夹边分别相等的两个三角形____;
(8)三边分别相等的两个三角形_____.
3. 等式的基本性质和将来要学到的不等式的基本性质也看做____________。
4.在等式或不等式中,一个量可以用它的等量来替换”.用符号表示就是:“如果a=b,b=c,那么a=c”, “ 如果a>b,b=c,那么a>c。我们把它们也作为基本事实,简单说成:____________.
5.除基本事实外,以前所学过的以及今后要学到的其他几何命题,都需要由基本事实、定义、已证实的结论及已知条件出发,通过____________的方法加以证实。6.____________叫做证明.
全等全等基本事实等量代换推理的过程逻辑推理1、“如果两个角是对顶角,那么这两个角相等”的条件是________________,结论是_________________。2、如图所示:证明:∵∠AOC与∠BOD是对顶角(已知)
∴∠AOC+∠AOD=180°,
∠AOD+∠BOD= 180(平角的定义)
∴∠AOC+∠AOD=∠AOD+∠BOD(等量代换)
∴∠AOC=∠BOD(等式的基本性质)
3、条件: ∠AOC与∠BOD是对顶角
结论:∠AOC=∠BOD
这两个角相等两个角是对顶角OCBAD 4、已知: ∠AOC与∠BOD是对顶角
求证:∠AOC=∠BOD
交流与探索活动一把经过推理得到证实的真命题叫做定理定理可以作为今后证明其他命题的依据。定理与定义和基本事实一样,具有普遍的意义。“如果两个角是对顶角,那么这两个角相等”称为对顶角的性质定理,简单说成:对顶角相等。活动二例1 求证:同角的余角相等
第一步:根据题意,画出图形.
先根据命题的条件即已知事项,画出图形,再根据命题
的结论的需要在图上标出必要的字母或符号,以便于叙述或
推理过程的表达.【归纳升华】第二步:结合图形,根据条件、结论,写出已知、求证.
把命题条件、结论中的文字语言转化为几何中的符号语言写在已知、求证中。
第三步:找出由已知推出求证的途径,写出“证明” .
证明过程应按照“前因后果”的次序书写,其中的每一步推理都要有依据,推理的依据只能是基本事实、已学过的定义、已经证明过的定理和已知条件,不能凭“想当然”。
证明的一般步骤巩固与练习求证:同角的补角相等(画出图形,写出已知、求证,证明)
四、小结反思:
小组内讨论交流,通过本节课的学习,你掌握了那些知识?还有那些疑问? 达标测试
一、选择题
1、“两点确定一条直线”这句话是( )
A、假命题 B、定义 C、基本事实 D、以上答案都不对
2、下列命题不是基本事实的是( )
A、两点确定一条直线
B、两直线平行,同位角相等
C、过直线外一点有且只有一条直线与这条直线平行;
D、同位角相等,两直线平行
CB二、填空题,
3、阅读并理解下列各题的证明过程,并在每步后的括号内填写该步推理的依据。
已知:如图,B,C是线段AD上的两点,且AB=CD。
求证:AC=BD.
证明:∵AB=CD( )
∴AB+BC=CD+BC( )
∴AC=BD( )线段和的定义等式的基本性质已知三、解答题
4、已知:如图,直线AB,CD相交于点O, 且∠AOC是直角。
求证:∠COB,∠BOD, ∠DOA都是直角。证明:∵ ∠AOC是直角(已知),
∴ ∠AOC= 90°( 直角的定义),
∵直线AB,CD相交于点O,(已知),
∴∠AOC+∠COB=180°(平角的定义),
∴ ∠COB=180°∠AOC= 90°(等式的基本性质),
∴ ∠COB是直角(直角的定义),
∵ ∠ AOC与∠ BOD是对顶角,∠COB于 ∠DOA是对顶角(已知),
∴ ∠ AOC=∠BOD, ∠COB= ∠DOA (对顶角的性质),
∴ ∠ BOD,∠DOA都是直角(等量代换)
∴ ∠COB, ∠BOD, ∠DOA都是直角
作业必做题:课本166页第2题、第3题
选做题:课本166页第4题再 见
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
