2018年春北师大版七年级数学下册活页测试卷单元测试(五)生活中的轴对称
文档属性
| 名称 | 2018年春北师大版七年级数学下册活页测试卷单元测试(五)生活中的轴对称 |  | |
| 格式 | zip | ||
| 文件大小 | 231.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-08 20:13:23 | ||
图片预览

文档简介
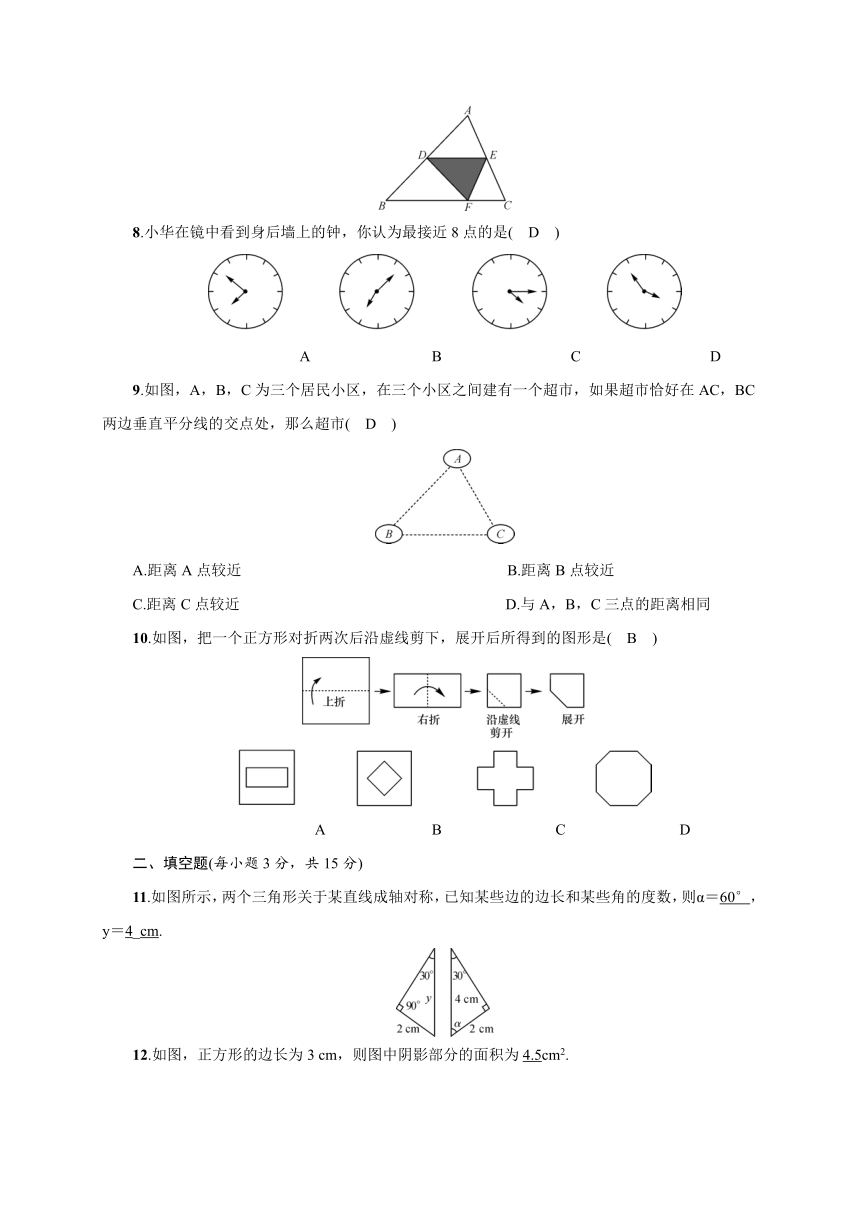
单元测试(五) 生活中的轴对称
(时间:45分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.下面有4个汽车标志图案,其中是轴对称图形的有( C )
A.1个 B.2个 C.3个 D.4个
2.下列英文字母中,经轴对称变换后形状不发生变化的是( B )
A.AHIOTXZ B.HIOX C.AHIOTNSQUVXC D.都不变形状
3.已知点P与点P1关于直线l成轴对称,则PP1与直线l的位置关系是( B )
A.平行 B.垂直 C.平行或垂直 D.不确定
4.如图,△ABC中,AB=AC,AD是中线,则下列结论中不一定正确的是( D )
A.∠B=∠C B.∠BAD=∠DAC C.∠ADB=∠ADC D.∠BAC=∠C
5.下列说法错误的是( C )
A.正方形有4条对称轴 B.一个角有1条对称轴
C.等腰三角形有3条对称轴 D.等边三角形有3条对称轴
6.如图,∠AOB的平分线上一点P到OA的距离为5,Q是OB上任意一点,则( A )
A.PQ大于或等于5 B.PQ大于5
C.PQ小于或等于5 D.PQ小于5
7.如图,点D为△ABC边AB的中点,将△ABC沿经过点D的直线折叠,使点A刚好落在BC边上的点F处,若∠B=46°,则∠BDF的度数为( A )
A.88° B.86° C.84° D.82°
8.小华在镜中看到身后墙上的钟,你认为最接近8点的是( D )
A B C D
9.如图,A,B,C为三个居民小区,在三个小区之间建有一个超市,如果超市恰好在AC,BC两边垂直平分线的交点处,那么超市( D )
A.距离A点较近 B.距离B点较近
C.距离C点较近 D.与A,B,C三点的距离相同
10.如图,把一个正方形对折两次后沿虚线剪下,展开后所得到的图形是( B )
A B C D
二、填空题(每小题3分,共15分)
11.如图所示,两个三角形关于某直线成轴对称,已知某些边的边长和某些角的度数,则α=60°,y=4_cm.
12.如图,正方形的边长为3 cm,则图中阴影部分的面积为4.5cm2.
13.如图,∠BAC=110°,若A,B关于直线MP对称,A,C关于直线NQ对称,则∠PAQ的度数是40°.
14.如图,在△ABC中,AB=AC,BC=BD,AD=DE=EB,则∠A等于45°.
15.加油站A和商店B在马路MN的同一侧(如图),A到MN的距离大于B到MN的距离,AB=7米,一个行人P在哪路MN上行走,问:当P道A的距离与P到B的距离之差最大时,这个差等于7米.
三、解答题(共55分)
16.(9分)如图,△ABC与△DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
解:如图所示.
17.(10分)电力工作人员栽完电线杆后,用两根等长的拉线把电线杆固定了(AB=AC),但有工作人员认为看上去有点倾斜,请你帮助工作人员测一下电线杆是否倾斜,并说明理由.
解:测量BD与DC,若BD=DC,说明D为BC中点,AD为△ABC的中线.
又因为△ABC是等腰三角形,所以AD是△ABC的高线.所以AD⊥BC,既电线杆不倾斜.
18.(10分)秋天红透的枫叶,总能勾起人们无尽的遐想,所以诗人杜牧说:“停车坐爱枫林晚,霜叶红于二月花.” 如图有半片枫叶,请以直线l为对称轴补画出枫叶的另一半.
解:作图如下:
19.(12分)如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A,B为垂足,AB交OM于点N,试说明:∠OAB=∠OBA.
解:因为OM平分∠POQ,MA⊥OP,MB⊥OQ,
所以MA=MB.所以△AMB是等腰三角形.
所以∠MAB=∠MBA.
又因为∠MAO=∠MBO=90°,
所以∠MAO-∠MAB=∠MBO-∠MBA,
即∠OAB=∠OBA.
20.(14分)如图,E,F分别是等边△ABC的边AB,AC上的点,且BE=AF,CE,BF交于点P.
(1)试说明:CE=BF;
(2)求∠BPC的度数.
解:(1)因为△ABC是等边三角形,所以BC=AB,∠A=∠EBC=60°.
在△BCE和△ABF中,
所以△BCE≌△ABF(SAS).所以CE=BF.
(2)因为△BCE≌△ABF,所以∠BCE=∠ABF.
所以∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60°.
所以∠BPC=180°-60°=120°.
(时间:45分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.下面有4个汽车标志图案,其中是轴对称图形的有( C )
A.1个 B.2个 C.3个 D.4个
2.下列英文字母中,经轴对称变换后形状不发生变化的是( B )
A.AHIOTXZ B.HIOX C.AHIOTNSQUVXC D.都不变形状
3.已知点P与点P1关于直线l成轴对称,则PP1与直线l的位置关系是( B )
A.平行 B.垂直 C.平行或垂直 D.不确定
4.如图,△ABC中,AB=AC,AD是中线,则下列结论中不一定正确的是( D )
A.∠B=∠C B.∠BAD=∠DAC C.∠ADB=∠ADC D.∠BAC=∠C
5.下列说法错误的是( C )
A.正方形有4条对称轴 B.一个角有1条对称轴
C.等腰三角形有3条对称轴 D.等边三角形有3条对称轴
6.如图,∠AOB的平分线上一点P到OA的距离为5,Q是OB上任意一点,则( A )
A.PQ大于或等于5 B.PQ大于5
C.PQ小于或等于5 D.PQ小于5
7.如图,点D为△ABC边AB的中点,将△ABC沿经过点D的直线折叠,使点A刚好落在BC边上的点F处,若∠B=46°,则∠BDF的度数为( A )
A.88° B.86° C.84° D.82°
8.小华在镜中看到身后墙上的钟,你认为最接近8点的是( D )
A B C D
9.如图,A,B,C为三个居民小区,在三个小区之间建有一个超市,如果超市恰好在AC,BC两边垂直平分线的交点处,那么超市( D )
A.距离A点较近 B.距离B点较近
C.距离C点较近 D.与A,B,C三点的距离相同
10.如图,把一个正方形对折两次后沿虚线剪下,展开后所得到的图形是( B )
A B C D
二、填空题(每小题3分,共15分)
11.如图所示,两个三角形关于某直线成轴对称,已知某些边的边长和某些角的度数,则α=60°,y=4_cm.
12.如图,正方形的边长为3 cm,则图中阴影部分的面积为4.5cm2.
13.如图,∠BAC=110°,若A,B关于直线MP对称,A,C关于直线NQ对称,则∠PAQ的度数是40°.
14.如图,在△ABC中,AB=AC,BC=BD,AD=DE=EB,则∠A等于45°.
15.加油站A和商店B在马路MN的同一侧(如图),A到MN的距离大于B到MN的距离,AB=7米,一个行人P在哪路MN上行走,问:当P道A的距离与P到B的距离之差最大时,这个差等于7米.
三、解答题(共55分)
16.(9分)如图,△ABC与△DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
解:如图所示.
17.(10分)电力工作人员栽完电线杆后,用两根等长的拉线把电线杆固定了(AB=AC),但有工作人员认为看上去有点倾斜,请你帮助工作人员测一下电线杆是否倾斜,并说明理由.
解:测量BD与DC,若BD=DC,说明D为BC中点,AD为△ABC的中线.
又因为△ABC是等腰三角形,所以AD是△ABC的高线.所以AD⊥BC,既电线杆不倾斜.
18.(10分)秋天红透的枫叶,总能勾起人们无尽的遐想,所以诗人杜牧说:“停车坐爱枫林晚,霜叶红于二月花.” 如图有半片枫叶,请以直线l为对称轴补画出枫叶的另一半.
解:作图如下:
19.(12分)如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A,B为垂足,AB交OM于点N,试说明:∠OAB=∠OBA.
解:因为OM平分∠POQ,MA⊥OP,MB⊥OQ,
所以MA=MB.所以△AMB是等腰三角形.
所以∠MAB=∠MBA.
又因为∠MAO=∠MBO=90°,
所以∠MAO-∠MAB=∠MBO-∠MBA,
即∠OAB=∠OBA.
20.(14分)如图,E,F分别是等边△ABC的边AB,AC上的点,且BE=AF,CE,BF交于点P.
(1)试说明:CE=BF;
(2)求∠BPC的度数.
解:(1)因为△ABC是等边三角形,所以BC=AB,∠A=∠EBC=60°.
在△BCE和△ABF中,
所以△BCE≌△ABF(SAS).所以CE=BF.
(2)因为△BCE≌△ABF,所以∠BCE=∠ABF.
所以∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60°.
所以∠BPC=180°-60°=120°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
