新课标人教A版高中数学必修三第三章第一节《3.1.3概率的基本性质》课件(共24张ppt)
文档属性
| 名称 | 新课标人教A版高中数学必修三第三章第一节《3.1.3概率的基本性质》课件(共24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 279.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-09 21:45:29 | ||
图片预览





文档简介
课件24张PPT。3.1.3 概率的基本性质
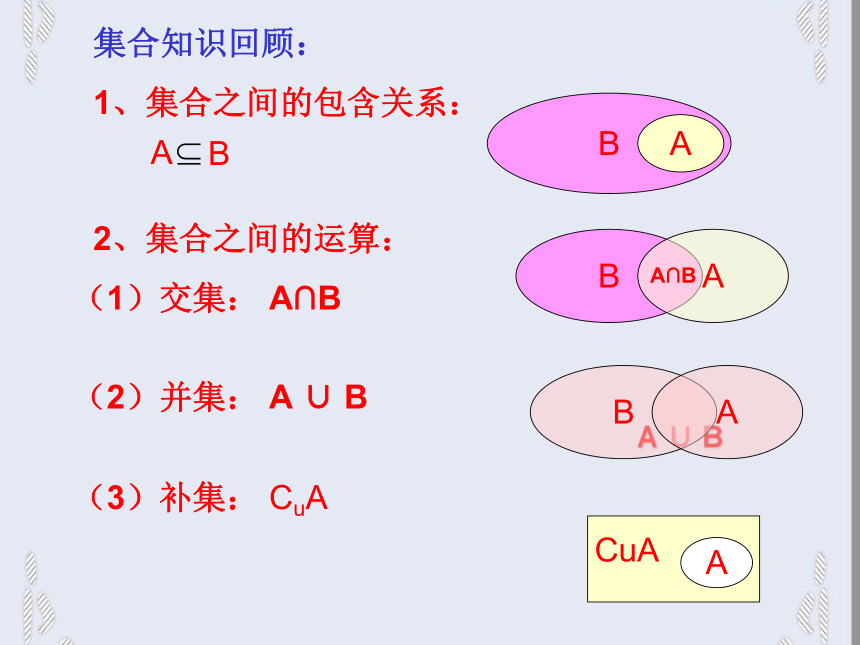
集合知识回顾:1、集合之间的包含关系:BA2、集合之间的运算:BA(1)交集: A∩B(2)并集: A ∪ B(3)补集: CuA ABA ∪ BBAA∩BACuA掷一个骰子,可以按如下定义事件,例如:事件A:出现1点事件B:出现2点事件C:出现3点事件D:出现的点数小于或等于3思考:事件D与事件A,B,C什么关系?我们把每一个结果可看作元素,而每一个事件可看作一个集合。
因此,事件之间的关系及运算几乎等价于集合之间的关系与运算。例如:A={出现1点}B={出现2点}C={出现3点}D={出现的点数小于或等于3}事件A:出现1点事件B:出现2点事件C:出现3点事件D:出现的点数小于或等于3事件的关系与运算 一般地,对于事件A和事件B,如果事件A发生,则事件B一定发生,
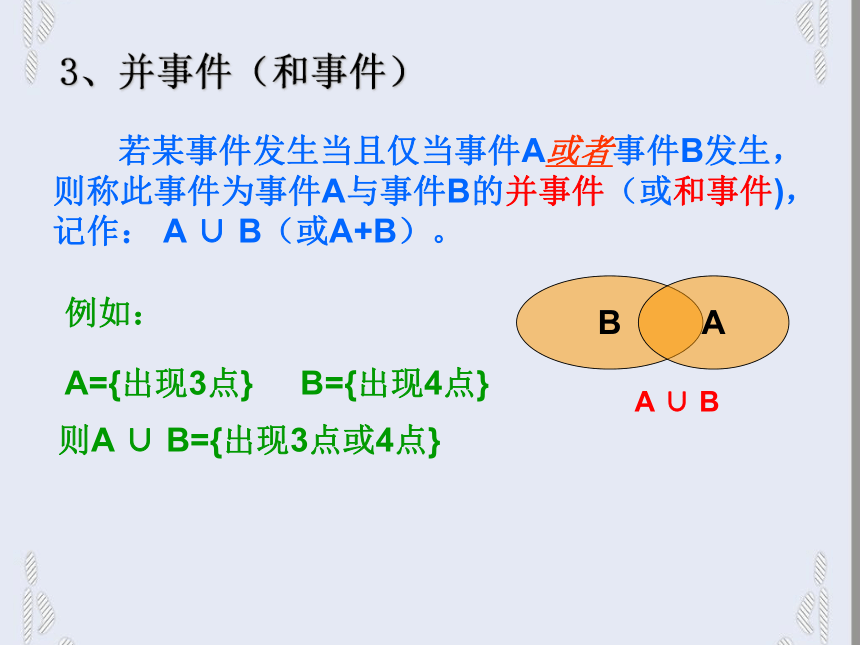
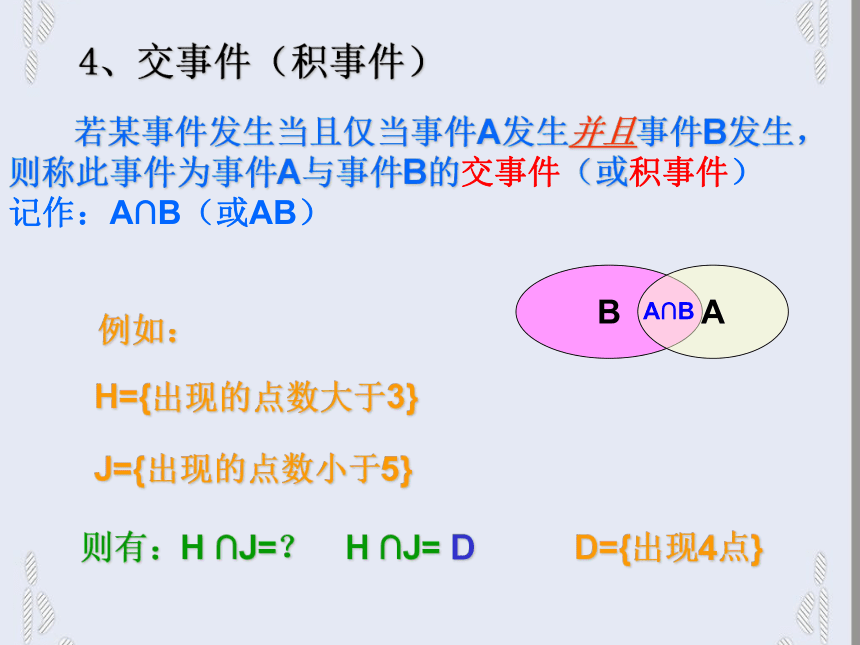
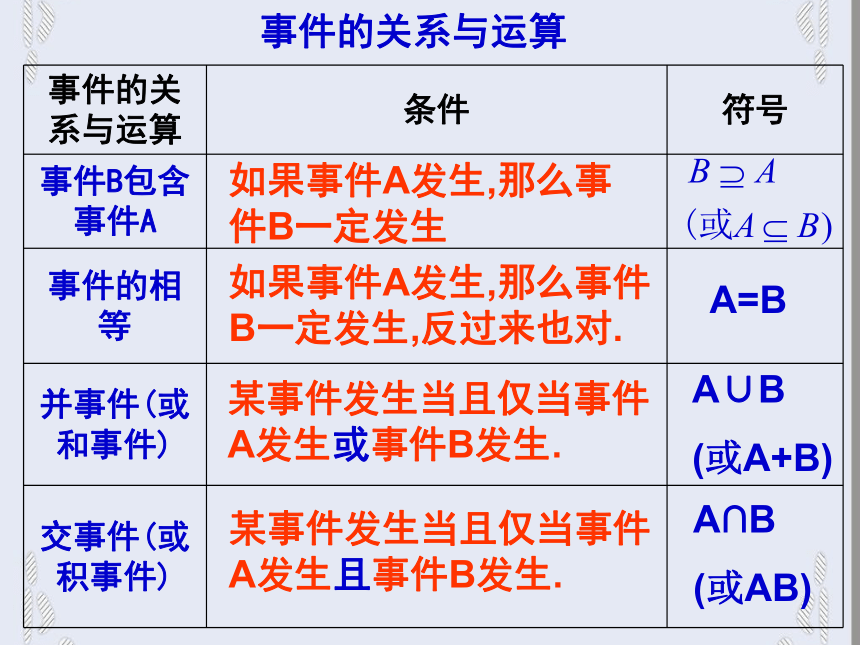
这时称事件B包含事件A(或称事件A包含于事件B),记作:A B(或B A)表示为:1、事件的包含关系BA例如:A={出现2点} B={出现的点数小于5}所以有A B我们把不可能事件记作?,任何事件都包含不可能事件 一般地,若B A,且A B,那么称事件A与事件B相等,记作:A=B。2、事件的相等关系例如:A={出现的点数不大于1} B={出现1点} 所以有 A=B注:两个事件相等也就是说这两个事件是同一个事件。 若某事件发生当且仅当事件A或者事件B发生, 则称此事件为事件A与事件B的并事件(或和事件), 记作: A ∪ B(或A+B)。3、并事件(和事件)BA例如:A={出现3点} B={出现4点}则A ∪ B={出现3点或4点}A ∪ B 若某事件发生当且仅当事件A发生并且事件B发生, 则称此事件为事件A与事件B的交事件(或积事件) 记作:A∩B(或AB) 4、交事件(积事件)BA例如:H={出现的点数大于3}J={出现的点数小于5}D={出现4点}则有:H ∩J=?A∩BH ∩J= D事件的关系与运算如果事件A发生,那么事件B一定发生如果事件A发生,那么事件B一定发生,反过来也对.A=B某事件发生当且仅当事件A发生或事件B发生.A∪B
(或A+B)某事件发生当且仅当事件A发生且事件B发生.A∩B
(或AB) 若A∩B为不可能事件( A∩B =? ),那么称事 件A与事件B互斥。 事件A与事件B互斥的含义是:这两个事件在任
何一次试验中都不能同时发生,可用图表示为:
5、互斥事件BA例如:D={出现4点} F={出现6点}M={出现的点数为偶数} N={出现的点数为奇数}则有:事件D与事件F互斥事件M与事件N互斥(2)下列各组事件中,不是互斥事件的是( )
一个射手进行一次射击,命中环数大于8与命中环数小于6
B. 统计一个班级数学期中考试成绩,平均分数不低于90分与平均分数不高于90分
C. 播种菜籽100粒,发芽90粒与发芽80粒
D. 检查某种产品,合格率高于70%与合格率为70%B例1(1)一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )
至多有一次中靶 B. 两次都不中靶
C. 只有一次中靶 D. 两次都不中靶D 若A∩B为不可能事件, A ∪ B为必然事件,那么 事件A与事件B互为对立事件。 事件A与事件B互为对立事件的含义是:这两个 事件在任何一次试验中有且仅有一个发生。6、对立事件M={出现的点数为偶数} N={出现的点数为奇数}例如:则有:M与N互为对立事件A∩B =?, P(A∪B )=1 AB例2. 从一堆产品(其中正品和次品都多于 2件)中任取 2件,观察正品件数和次品件数,判断下列每对事件是不是互斥事件,若是,再判断它们是不是对立事件:
(1)恰好有 1 件次品和恰好有 2 件次品;
(2)至少有 1 件次品和全是次品;
(3)至少有 1 件正品和至少有 1件次品;
(4)至少有 1 件次品和全是正品。①正正
②一正一次
③次次②与③:互斥不对立②、③与③:不互斥不对立①、②与②、③:不互斥不对立②、③与①:互斥且对立互斥事件与对立事件的区别与联系联系:都是两个事件的关系区别:
互斥事件: 不同时发生,但并非至少有一个发生; 对立事件: 两个事件不同时发生,必有一个发生对立事件是互斥事件,是互斥中的特殊情况但互斥事件不一定是对立事件概率的几个基本性质:1、任何事件之间的概率都在0~1之间:2、必然事件的概率为1。若B为必然事件,则有:P(B)=13、不可能事件的概率为0。如C为不可能事件,则有:P(C)=00≤P(A)≤1如果事件A与事件B互斥,则有 P( A ∪ B )=P(A)+P(B)
概率的加法公式4、概率的加法公式5、若事件A与事件B互为对立事件,则有:=1所以 P(A)=1 - P(B)P( A ∪ B )=P(A)+P(B)注意:1.利用上述公式求概率时,首先要确定
两事件是否互斥,如果没有这一条件,该公式
不能运用。即当两事件不互斥时,应有:如果事件A与事件B互斥,则
P (A ? B)= P (A) + P (B)P (A ? B)= P (A) + P (B) - P(???)2.上述公式可推广,即如果随机事件A1,A2,
……,An中任何两个都是互斥事件,那么有P (A1 ? A2 ?… ?An)= P (A1) + P (A2)+…+P(?n)一般地,在解决比较复杂的事件的概率问题时,常常把复杂事件分解为几个互斥事件,借助该推广公式解决。例3.如果从不包括大小王的52张扑克牌中随机抽取一张,那么 取到红心(事件A)的概率是1/4,取到方块(事件B)的概率是1/4。问:
(1)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?(2)因为C与D是互斥事件,又由于C∪D为必然事件,
所以C与D互为对立事件,所以例4.如果事件A,B是互斥事件,则下列说法正确的
个数有( )A. 2个 B. 3个 C. 4个 D. 5个A例5.某射手射击一次,射中10环、9环、8环、7环的概率分别是0.24、0.28、0.19、 0.16,计算这名射手射击一次
1)射中10环或9环的概率;
2)至少射中7环的概率.
3)射中环数不足8环的概率.0.520.870.29例6.盒中装有颜色各异的小球12只,其中5红、4黑、2白、1绿,从中任取1球.求:
(1)取出球的颜色是红或黑的概率;
(2)取出球的颜色是红或黑或白的概率.
因此,事件之间的关系及运算几乎等价于集合之间的关系与运算。例如:A={出现1点}B={出现2点}C={出现3点}D={出现的点数小于或等于3}事件A:出现1点事件B:出现2点事件C:出现3点事件D:出现的点数小于或等于3事件的关系与运算 一般地,对于事件A和事件B,如果事件A发生,则事件B一定发生,
这时称事件B包含事件A(或称事件A包含于事件B),记作:A B(或B A)表示为:1、事件的包含关系BA例如:A={出现2点} B={出现的点数小于5}所以有A B我们把不可能事件记作?,任何事件都包含不可能事件 一般地,若B A,且A B,那么称事件A与事件B相等,记作:A=B。2、事件的相等关系例如:A={出现的点数不大于1} B={出现1点} 所以有 A=B注:两个事件相等也就是说这两个事件是同一个事件。 若某事件发生当且仅当事件A或者事件B发生, 则称此事件为事件A与事件B的并事件(或和事件), 记作: A ∪ B(或A+B)。3、并事件(和事件)BA例如:A={出现3点} B={出现4点}则A ∪ B={出现3点或4点}A ∪ B 若某事件发生当且仅当事件A发生并且事件B发生, 则称此事件为事件A与事件B的交事件(或积事件) 记作:A∩B(或AB) 4、交事件(积事件)BA例如:H={出现的点数大于3}J={出现的点数小于5}D={出现4点}则有:H ∩J=?A∩BH ∩J= D事件的关系与运算如果事件A发生,那么事件B一定发生如果事件A发生,那么事件B一定发生,反过来也对.A=B某事件发生当且仅当事件A发生或事件B发生.A∪B
(或A+B)某事件发生当且仅当事件A发生且事件B发生.A∩B
(或AB) 若A∩B为不可能事件( A∩B =? ),那么称事 件A与事件B互斥。 事件A与事件B互斥的含义是:这两个事件在任
何一次试验中都不能同时发生,可用图表示为:
5、互斥事件BA例如:D={出现4点} F={出现6点}M={出现的点数为偶数} N={出现的点数为奇数}则有:事件D与事件F互斥事件M与事件N互斥(2)下列各组事件中,不是互斥事件的是( )
一个射手进行一次射击,命中环数大于8与命中环数小于6
B. 统计一个班级数学期中考试成绩,平均分数不低于90分与平均分数不高于90分
C. 播种菜籽100粒,发芽90粒与发芽80粒
D. 检查某种产品,合格率高于70%与合格率为70%B例1(1)一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )
至多有一次中靶 B. 两次都不中靶
C. 只有一次中靶 D. 两次都不中靶D 若A∩B为不可能事件, A ∪ B为必然事件,那么 事件A与事件B互为对立事件。 事件A与事件B互为对立事件的含义是:这两个 事件在任何一次试验中有且仅有一个发生。6、对立事件M={出现的点数为偶数} N={出现的点数为奇数}例如:则有:M与N互为对立事件A∩B =?, P(A∪B )=1 AB例2. 从一堆产品(其中正品和次品都多于 2件)中任取 2件,观察正品件数和次品件数,判断下列每对事件是不是互斥事件,若是,再判断它们是不是对立事件:
(1)恰好有 1 件次品和恰好有 2 件次品;
(2)至少有 1 件次品和全是次品;
(3)至少有 1 件正品和至少有 1件次品;
(4)至少有 1 件次品和全是正品。①正正
②一正一次
③次次②与③:互斥不对立②、③与③:不互斥不对立①、②与②、③:不互斥不对立②、③与①:互斥且对立互斥事件与对立事件的区别与联系联系:都是两个事件的关系区别:
互斥事件: 不同时发生,但并非至少有一个发生; 对立事件: 两个事件不同时发生,必有一个发生对立事件是互斥事件,是互斥中的特殊情况但互斥事件不一定是对立事件概率的几个基本性质:1、任何事件之间的概率都在0~1之间:2、必然事件的概率为1。若B为必然事件,则有:P(B)=13、不可能事件的概率为0。如C为不可能事件,则有:P(C)=00≤P(A)≤1如果事件A与事件B互斥,则有 P( A ∪ B )=P(A)+P(B)
概率的加法公式4、概率的加法公式5、若事件A与事件B互为对立事件,则有:=1所以 P(A)=1 - P(B)P( A ∪ B )=P(A)+P(B)注意:1.利用上述公式求概率时,首先要确定
两事件是否互斥,如果没有这一条件,该公式
不能运用。即当两事件不互斥时,应有:如果事件A与事件B互斥,则
P (A ? B)= P (A) + P (B)P (A ? B)= P (A) + P (B) - P(???)2.上述公式可推广,即如果随机事件A1,A2,
……,An中任何两个都是互斥事件,那么有P (A1 ? A2 ?… ?An)= P (A1) + P (A2)+…+P(?n)一般地,在解决比较复杂的事件的概率问题时,常常把复杂事件分解为几个互斥事件,借助该推广公式解决。例3.如果从不包括大小王的52张扑克牌中随机抽取一张,那么 取到红心(事件A)的概率是1/4,取到方块(事件B)的概率是1/4。问:
(1)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?(2)因为C与D是互斥事件,又由于C∪D为必然事件,
所以C与D互为对立事件,所以例4.如果事件A,B是互斥事件,则下列说法正确的
个数有( )A. 2个 B. 3个 C. 4个 D. 5个A例5.某射手射击一次,射中10环、9环、8环、7环的概率分别是0.24、0.28、0.19、 0.16,计算这名射手射击一次
1)射中10环或9环的概率;
2)至少射中7环的概率.
3)射中环数不足8环的概率.0.520.870.29例6.盒中装有颜色各异的小球12只,其中5红、4黑、2白、1绿,从中任取1球.求:
(1)取出球的颜色是红或黑的概率;
(2)取出球的颜色是红或黑或白的概率.
