直线、射线、线段复习课件
图片预览









文档简介
课件55张PPT。1直线、射线、线段
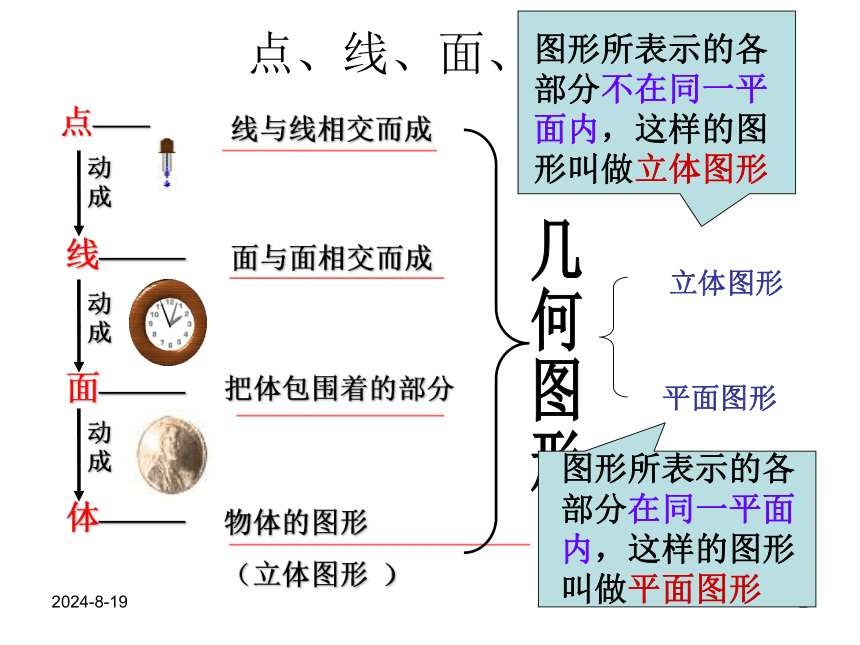
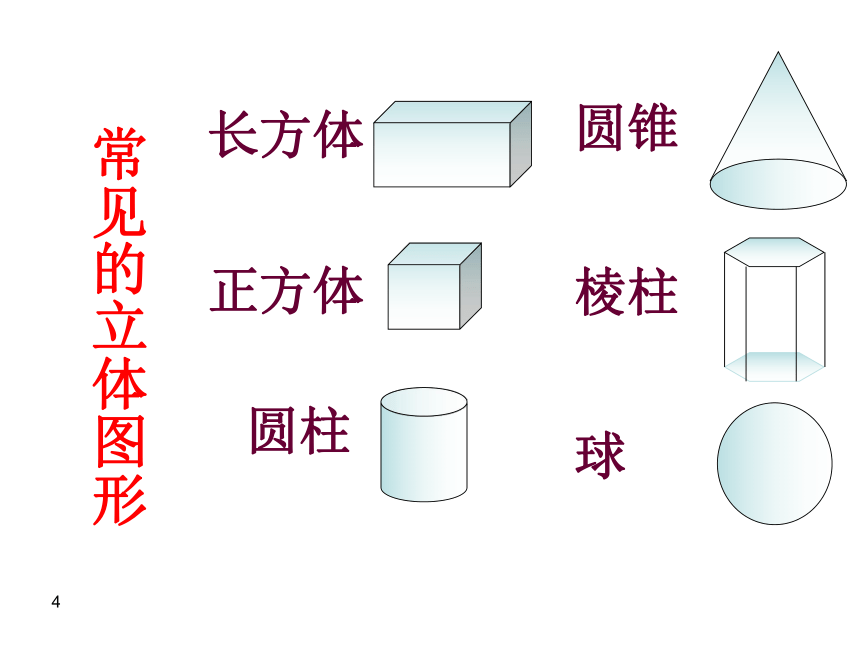
专题复习2018-10-111点、线、面、体点——线———体———面———几何图形平面图形立体图形1常见的平面图形长方形正方形三角形五边形 圆形六边形1常见的立体图形
圆柱圆锥
棱柱
球
正方体长方体11. 线段、射线、直线的区别:
填表:
012两方一方不延伸不能度量不能度量 能度量线段、射线、直线的联系:射线是直线的一部分,线段是射线的一部
分,也是直线的一部分.1表示:线段 AB(或线段BA)a表示:线段 aA表示:射线 OA表示:直线 AB(或直线BA)l表示:直线l线段、射线、直线的表示方法2018-10-111试比较线段AB、CD的长短。(1) 度量法 用刻度尺量出线段AB长4cm,线段CD长4.5cm,所以线段AB比线段CD短。(记作AB<CD 或 CD >AB)(2) 叠合法 将一线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上。1直线和线段的性质2.直线的性质
3.线段的性质:在所有联接两点的线中,线段最短。
简单说成:两点之间,线段最短。①直线公理:经过两点有且只有一条直线.
②两条直线相交只有一个交点.1 线段中点的定义: 如图, 点C把线段AB分成相等的两条线段AC和BC,点C叫做线段AB的中点。ABC若AC=BC;
则C是线段AB的中点若C是线段AB的中点;
则AC=BC。(或者AC=BC=?AB)(或者AC=BC=?AB)1.射击时,总是用一只眼瞄准目标,这依据的数学知识是_________________.
2.点M在线段AB上,且AM=MB,则点M叫线段AB的___,若AM=6cm,则AB= cm;
3.如图,从A到B有3条路径,最短的路径是___,理由是_______________.1、如果点C在AB上,下列表达式①AC=AB;②AB=2BC;③AC=BC;④AC+BC=AB中, 能表示C是AB中点的有( )
A.1个 B.2个 C.3个 D.4个
2、如图,在直线I上顺次取A、B、C、D四点,则AC=______+BC=AD-_____,
AC+BD- BC=________.
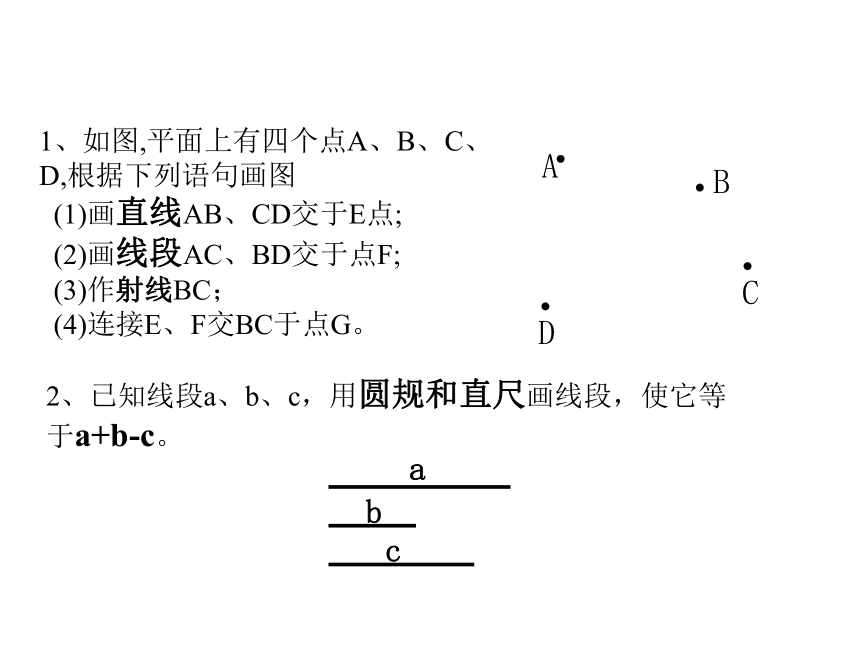
1、如图,平面上有四个点A、B、C、D,根据下列语句画图
(1)画直线AB、CD交于E点;
(2)画线段AC、BD交于点F;
(3)作射线BC;
(4)连接E、F交BC于点G。2、已知线段a、b、c,用圆规和直尺画线段,使它等于a+b-c。6、如图,在正方体两个相距最远的顶点处逗留着一只苍蝇和一只蜘蛛.
①如果蜘蛛沿着棱爬到苍蝇处,最短的路线有几条?
②如果蜘蛛从正方体的表面爬,最短的路线怎么爬?请你画图并说明你的理由?7、一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C,怎样爬所走的路程最短? 第三章复习直线、射线、线段通过本节课的复习你的目标是1、认识图形的基本性质、变换、位置关系,掌握基本的识图、作图技能;
2、结合具体图形,理解直线、射线、线段的含义、表达方法及性质;
3、体验数、符号和图形是有效地描述现实世界的重要手段。下面的知识点你掌握了吗?知识点1:线段
(1)线段的概念:它是直线的一部分,它的长度是有限的,它有两个端点.
(2)线段的表示方法:可用它的两个端点的大写字母或用一个小写字母来表示.
(3)线段的画法:可用直尺先量出线段的长度,再画一条等于这个长度的线段.(4)线段的基本性质:两点之间线段最短.
(5)两点间的距离:连结两点的线段的长度,叫做这两点间的距离.
(6)线段的特点:有两个端点,不能向任何一方伸展,可以度量,可以比较长短.
知识点2:射线(1)射线的概念:把线段向一方无限延伸所形成的图形叫做射线.
(2)射线的表示方法:可用两个大写字母表示,第一个大写字母表示它的端点;也可用一个小写字母表示.
(3)射线的特点:只有一个端点,向一方无限延伸,无法度量,不能比较长短.知识点3:直线(1)直线的概念:把线段向两方无限延伸所形成的图形.
(2)直线的表示方法:可用这条直线上的两个点表示,也可以用一个小写字母表示.
(3)直线的基本性质:经过两点有一条直线,并且只有一条直线.
(4)直线的特点:没有端点,向两方无限延伸,不可度量,不能比较大小.知识点4:线段的中点把一条线段分成两条相等线段的点,叫做线段的中点.另外线段还有三等分点、四等分点等。你能解决下列问题吗?1、图中共有几条线段?几条射线?几条直线?能用字母表示出来的分别用字母表示出来。ABC2、判断下列说法是否正确:
(1)延长射线OA;(2)直线比射线长,射线比线段长;(3)直线AB和直线CD相交于点m;(4)A、B两点间的距离就是连结A、B两点间的线段。3.用一个钉子把一根细木条钉在木板上,用手拔木条,木条能转动,这表明___________;用两个钉子把细木条钉在木板上,就能固定细木条,这说明______________________.4.如图所示,一只蚂蚁要从圆柱体A点沿表面尽可能地爬到B点,因为那里有它的食物,而它饿得快不行了,怎么爬行路线最短?··AB5.有关线段的计算问题(1)如图,A、B、C、D是直线l上顺次四点,且线段AC=5,BD=4,则线段AB-CD=_____.ABCD l(2)如图,AC=8cm,CB=6cm,如果O是线段AB的中点,求线段OC的长度。ABCO(3)已知AB=16cm,C是AB上一点,且AC=10cm,D为AC的中点,E是BC的中点,求线段DE的长。(4)同一直线上有A、B、C、D四点,已知AD= DB,AC= CB,且CD=4cm,求AB的长。5959(5)已知线段AC和线段BC在同一直线上,若AC=5.6cm,BC=2.4cm.求线段AC的中点与线段BC中点之间的距离。探究一、有关距离问题1.如图,在一条笔直的公路a两侧,分别有A、B两个村庄,现要在公路a上建一个汽车站C,使汽车站到A、B两村距离之和最小,问汽车站C的位置应该如何确定?aAB··2.平原上有A、B、C、D四个村庄,如图所示,为解决当地缺水问题,政府准备投资修建一个蓄水池,不考虑其他因素,请你画图确定蓄水池H的位置,使它与四个村庄的距离之和最小.····ABCD3.如图,蚂蚁在圆锥底边的点A处,它想绕圆锥爬行一周后回到点A处,你能画出它爬行的最短路线吗?A(4).如图所示,洋河酒厂有三个住宅区A、B、C各分别住有职工30人、15人、10人,且这三个区在酒家大道上(A、B、C)三点共线,已知AB=100米,BC=200米.为了方便职工上下班,该厂的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在_____区.ABC探究二:画一画,数一数,再找规律1.在平面内有n个点(n≥3),其中没有任何三个点在一条直线上,如果过任意两点画一条直线,这n个点可以画多少条直线?2.一条直线将平面分成两部分,两条直线将平面分成四部分,那么三条直线将平面 最多分成几部分?四条直线将平面最多分成几部分?n条直线呢?3.如图,以A0,A1,A2,A3,…,An为端点的线段有几条?A0A1A2A3A4An-1An4.往返于A、B两地的客车,中途停靠三个站。
(1)问有多少种不同的票价?
(2)要准备多少种车票?ABCDE善于总结才能提高通过本节课的复习,你对这部分的知识掌握得如何,对你的同学说一说,你认为应该注意哪些方面。我觉得本节课该注意….作业布置一、课堂作业:
1、《补充习题》P36第5题;
2、《补充习题》P42第9题。
二、课外作业:
课本、《补充习题》、《课时作业》上的相关习题。保持学习的积极心态和努力向上的进取精神是获得成绩的有效途径!下面的知识点你掌握了吗?知识点1:线段
(1)线段的概念:它是直线的一部分,它的长度是有限的,它有两个端点.
(2)线段的表示方法:可用它的两个端点的大写字母或用一个小写字母来表示.
(3)线段的画法:可用直尺先量出线段的长度,再画一条等于这个长度的线段.(4)线段的基本性质:两点之间线段最短.
(5)两点间的距离:连结两点的线段的长度,叫做这两点间的距离.
(6)线段的特点:有两个端点,不能向任何一方伸展,可以度量,可以比较长短.
下面的知识点你掌握了吗?知识点2:射线(1)射线的概念:把线段向一方无限延伸所形成的图形叫做射线.
(2)射线的表示方法:可用两个大写字母表示,第一个大写字母表示它的端点;也可用一个小写字母表示.
(3)射线的特点:只有一个端点,向一方无限延伸,无法度量,不能比较长短.知识点3:直线(1)直线的概念:把线段向两方无限延伸所形成的图形.
(2)直线的表示方法:可用这条直线上的两个点表示,也可以用一个小写字母表示.
(3)直线的基本性质:经过两点有一条直线,并且只有一条直线.
(4)直线的特点:没有端点,向两方无限延伸,不可度量,不能比较大小.你能解决下列问题吗?1、图中共有几条线段?几条射线?几条直线?能用字母表示出来的分别用字母表示出来。ABC2、判断下列说法是否正确:
(1)延长射线OA;(2)直线比射线长,射线比线段长;(3)直线AB和直线CD相交于点m;(4)A、B两点间的距离就是连结A、B两点间的线段。3.用一个钉子把一根细木条钉在木板上,用手拔木条,木条能转动,这表明___________ ;用两个钉子把 细木条钉在木板上,就能固定细木条,这说明________________。4.如图所示,一只蚂蚁要从圆柱体A点沿表面尽可能地爬到B点,因为那里有它的食物,而它饿得快不行了,怎么爬行路线最短?··AB过一点有无数条直线两点确定一条直线5.有关线段的计算问题(1)如图,A、B、C、D是直线l上顺次四点,且线段AC=5,BD=4,则线段AB-CD=_____.ABCD l(2)如图,AC=8cm,CB=6cm,如果O是线段AB的中点,求线段OC的长度。ABCO(3)已知AB=16cm,C是AB上一点,且AC=10cm,D为AC的中点,E是BC的中点,求线段DE的长。(4)同一直线上有A、B、C、D四点,已知AD= DB,AC= CB,且CD=4cm,求AB的长。(5)已知线段AC和线段BC在同一直线上,若AC=5.6cm,BC=2.4cm.求线段AC的中点与线段BC中点之间的距离。探究一、有关距离问题1.如图,在一条笔直的公路a两侧,分别有A、B两个村庄,现要在公路a上建一个汽车站C,使汽车站到A、B两村距离之和最小,问汽车站C的位置应该如何确定?aAB··2.平原上有A、B、C、D四个村庄,如图所示,为解决当地缺水问题,政府准备投资修建一个蓄水池,不考虑其他因素,请你画图确定蓄水池H的位置,使它与四个村庄的距离之和最小.····ABCD3.如图,蚂蚁在圆锥底边的点A处,它想绕圆锥爬行一周后回到点A处,你能画出它爬行的最短路线吗?A(4).如图所示,洋河酒厂有三个住宅区A、B、C各分别住有职工30人、15人、10人,且这三个区在酒家大道上(A、B、C)三点共线,已知AB=100米,BC=200米.为了方便职工上下班,该厂的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在_____区.ABC探究二:画一画,数一数,再找规律1.在平面内有n个点(n≥3),其中没有任何三个点在一条直线上,如果过任意两点画一条直线,这n个点可以画多少条直线?2.一条直线将平面分成两部分,两条直线将平面分成四部分,那么三条直线将平面 最多分成几部分?四条直线将平面最多分成几部分?n条直线呢?4.2线段的长短比较1 度量法2 叠合法3 线段中点的定义和简单作法。直线、射线、线段的比较二、直线、 射线、 线段1.直线、射线、线段的区别和联系
(1,)射线、线段都是直线的一部分,它们之间又有紧密的
联系;在直线上取一点,可以将该直线分成两条射线,取
两点可以得到一条线段和四条射线;把射线反向延长或
者把线段两方延长就可以得到直线。
(2.) 列表比较有关概念点、线段、射线、直线
* 线和线相交的地方是点(point)。
* 点通常表示一个物体的位置。例如,在交通图上用点来表示城市的位置。
* 直线上两个点和它们之间的部分叫做线段(line segment),这两个点叫做线段的端点。
在日常生活中,一根拉紧的绳子、一根竹竿、人行横道线都给我们以线段的形象。
* 把线段向一方无限延伸所形成的图形叫做射线(ray)。
* 把线段向两方无限延伸所形成的图形叫做直线
(straight line)。
(2)线段的中点
把一条线段分成两条相等线段的点,叫做这条线段的中点(middle point)。
2.线段的大小和比较
(1)线段的长短比较度量法叠合法AB=BC=ACAC=2AB=2BC例如:点B是线段AC的中点. . .ABC则有:(3)线段的三等分点
把一条线段分成三条相等线段的两个点,叫做这条线段的三等分点。. . . .A B C DAB=BC=CD=ADAD=3AB=3BC=3CD(4)画一条线段等于已知线段
注意耶用尺规作图法(5)两点的距离与线段的区别
两点的距离是指连接两点间的线段的长度,是一个数量;
而线段本身是图形.(6)线段的和、差
a.线段的和A B C. . .AC=AB+BCb.线段的差M N P. . .MN=MP-NPNP=MP-MN 例4 已知∠α和∠β互为补角,并且∠β的一半比∠α小30o,求∠α、∠β. 解:设∠α=xo,则∠β=180o-xo.根据题意 ∠β=2(∠α-30o),得 180- x=2(x -30),解得 x=80.所以 ,∠α=80o,∠β=100o. 例3 点A,B,C 在同一条直线上,
AB=3 cm,BC=1 cm.求AC的长.解:(1)如图①,因AB=3 ,BC=1,
所以,AC=AB+BC=3+1=4(cm).
(2)如图②,因AB=3,BC=1,
所以AC=AB-BC=3-1=2(cm).
圆柱圆锥
棱柱
球
正方体长方体11. 线段、射线、直线的区别:
填表:
012两方一方不延伸不能度量不能度量 能度量线段、射线、直线的联系:射线是直线的一部分,线段是射线的一部
分,也是直线的一部分.1表示:线段 AB(或线段BA)a表示:线段 aA表示:射线 OA表示:直线 AB(或直线BA)l表示:直线l线段、射线、直线的表示方法2018-10-111试比较线段AB、CD的长短。(1) 度量法 用刻度尺量出线段AB长4cm,线段CD长4.5cm,所以线段AB比线段CD短。(记作AB<CD 或 CD >AB)(2) 叠合法 将一线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上。1直线和线段的性质2.直线的性质
3.线段的性质:在所有联接两点的线中,线段最短。
简单说成:两点之间,线段最短。①直线公理:经过两点有且只有一条直线.
②两条直线相交只有一个交点.1 线段中点的定义: 如图, 点C把线段AB分成相等的两条线段AC和BC,点C叫做线段AB的中点。ABC若AC=BC;
则C是线段AB的中点若C是线段AB的中点;
则AC=BC。(或者AC=BC=?AB)(或者AC=BC=?AB)1.射击时,总是用一只眼瞄准目标,这依据的数学知识是_________________.
2.点M在线段AB上,且AM=MB,则点M叫线段AB的___,若AM=6cm,则AB= cm;
3.如图,从A到B有3条路径,最短的路径是___,理由是_______________.1、如果点C在AB上,下列表达式①AC=AB;②AB=2BC;③AC=BC;④AC+BC=AB中, 能表示C是AB中点的有( )
A.1个 B.2个 C.3个 D.4个
2、如图,在直线I上顺次取A、B、C、D四点,则AC=______+BC=AD-_____,
AC+BD- BC=________.
1、如图,平面上有四个点A、B、C、D,根据下列语句画图
(1)画直线AB、CD交于E点;
(2)画线段AC、BD交于点F;
(3)作射线BC;
(4)连接E、F交BC于点G。2、已知线段a、b、c,用圆规和直尺画线段,使它等于a+b-c。6、如图,在正方体两个相距最远的顶点处逗留着一只苍蝇和一只蜘蛛.
①如果蜘蛛沿着棱爬到苍蝇处,最短的路线有几条?
②如果蜘蛛从正方体的表面爬,最短的路线怎么爬?请你画图并说明你的理由?7、一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C,怎样爬所走的路程最短? 第三章复习直线、射线、线段通过本节课的复习你的目标是1、认识图形的基本性质、变换、位置关系,掌握基本的识图、作图技能;
2、结合具体图形,理解直线、射线、线段的含义、表达方法及性质;
3、体验数、符号和图形是有效地描述现实世界的重要手段。下面的知识点你掌握了吗?知识点1:线段
(1)线段的概念:它是直线的一部分,它的长度是有限的,它有两个端点.
(2)线段的表示方法:可用它的两个端点的大写字母或用一个小写字母来表示.
(3)线段的画法:可用直尺先量出线段的长度,再画一条等于这个长度的线段.(4)线段的基本性质:两点之间线段最短.
(5)两点间的距离:连结两点的线段的长度,叫做这两点间的距离.
(6)线段的特点:有两个端点,不能向任何一方伸展,可以度量,可以比较长短.
知识点2:射线(1)射线的概念:把线段向一方无限延伸所形成的图形叫做射线.
(2)射线的表示方法:可用两个大写字母表示,第一个大写字母表示它的端点;也可用一个小写字母表示.
(3)射线的特点:只有一个端点,向一方无限延伸,无法度量,不能比较长短.知识点3:直线(1)直线的概念:把线段向两方无限延伸所形成的图形.
(2)直线的表示方法:可用这条直线上的两个点表示,也可以用一个小写字母表示.
(3)直线的基本性质:经过两点有一条直线,并且只有一条直线.
(4)直线的特点:没有端点,向两方无限延伸,不可度量,不能比较大小.知识点4:线段的中点把一条线段分成两条相等线段的点,叫做线段的中点.另外线段还有三等分点、四等分点等。你能解决下列问题吗?1、图中共有几条线段?几条射线?几条直线?能用字母表示出来的分别用字母表示出来。ABC2、判断下列说法是否正确:
(1)延长射线OA;(2)直线比射线长,射线比线段长;(3)直线AB和直线CD相交于点m;(4)A、B两点间的距离就是连结A、B两点间的线段。3.用一个钉子把一根细木条钉在木板上,用手拔木条,木条能转动,这表明___________;用两个钉子把细木条钉在木板上,就能固定细木条,这说明______________________.4.如图所示,一只蚂蚁要从圆柱体A点沿表面尽可能地爬到B点,因为那里有它的食物,而它饿得快不行了,怎么爬行路线最短?··AB5.有关线段的计算问题(1)如图,A、B、C、D是直线l上顺次四点,且线段AC=5,BD=4,则线段AB-CD=_____.ABCD l(2)如图,AC=8cm,CB=6cm,如果O是线段AB的中点,求线段OC的长度。ABCO(3)已知AB=16cm,C是AB上一点,且AC=10cm,D为AC的中点,E是BC的中点,求线段DE的长。(4)同一直线上有A、B、C、D四点,已知AD= DB,AC= CB,且CD=4cm,求AB的长。5959(5)已知线段AC和线段BC在同一直线上,若AC=5.6cm,BC=2.4cm.求线段AC的中点与线段BC中点之间的距离。探究一、有关距离问题1.如图,在一条笔直的公路a两侧,分别有A、B两个村庄,现要在公路a上建一个汽车站C,使汽车站到A、B两村距离之和最小,问汽车站C的位置应该如何确定?aAB··2.平原上有A、B、C、D四个村庄,如图所示,为解决当地缺水问题,政府准备投资修建一个蓄水池,不考虑其他因素,请你画图确定蓄水池H的位置,使它与四个村庄的距离之和最小.····ABCD3.如图,蚂蚁在圆锥底边的点A处,它想绕圆锥爬行一周后回到点A处,你能画出它爬行的最短路线吗?A(4).如图所示,洋河酒厂有三个住宅区A、B、C各分别住有职工30人、15人、10人,且这三个区在酒家大道上(A、B、C)三点共线,已知AB=100米,BC=200米.为了方便职工上下班,该厂的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在_____区.ABC探究二:画一画,数一数,再找规律1.在平面内有n个点(n≥3),其中没有任何三个点在一条直线上,如果过任意两点画一条直线,这n个点可以画多少条直线?2.一条直线将平面分成两部分,两条直线将平面分成四部分,那么三条直线将平面 最多分成几部分?四条直线将平面最多分成几部分?n条直线呢?3.如图,以A0,A1,A2,A3,…,An为端点的线段有几条?A0A1A2A3A4An-1An4.往返于A、B两地的客车,中途停靠三个站。
(1)问有多少种不同的票价?
(2)要准备多少种车票?ABCDE善于总结才能提高通过本节课的复习,你对这部分的知识掌握得如何,对你的同学说一说,你认为应该注意哪些方面。我觉得本节课该注意….作业布置一、课堂作业:
1、《补充习题》P36第5题;
2、《补充习题》P42第9题。
二、课外作业:
课本、《补充习题》、《课时作业》上的相关习题。保持学习的积极心态和努力向上的进取精神是获得成绩的有效途径!下面的知识点你掌握了吗?知识点1:线段
(1)线段的概念:它是直线的一部分,它的长度是有限的,它有两个端点.
(2)线段的表示方法:可用它的两个端点的大写字母或用一个小写字母来表示.
(3)线段的画法:可用直尺先量出线段的长度,再画一条等于这个长度的线段.(4)线段的基本性质:两点之间线段最短.
(5)两点间的距离:连结两点的线段的长度,叫做这两点间的距离.
(6)线段的特点:有两个端点,不能向任何一方伸展,可以度量,可以比较长短.
下面的知识点你掌握了吗?知识点2:射线(1)射线的概念:把线段向一方无限延伸所形成的图形叫做射线.
(2)射线的表示方法:可用两个大写字母表示,第一个大写字母表示它的端点;也可用一个小写字母表示.
(3)射线的特点:只有一个端点,向一方无限延伸,无法度量,不能比较长短.知识点3:直线(1)直线的概念:把线段向两方无限延伸所形成的图形.
(2)直线的表示方法:可用这条直线上的两个点表示,也可以用一个小写字母表示.
(3)直线的基本性质:经过两点有一条直线,并且只有一条直线.
(4)直线的特点:没有端点,向两方无限延伸,不可度量,不能比较大小.你能解决下列问题吗?1、图中共有几条线段?几条射线?几条直线?能用字母表示出来的分别用字母表示出来。ABC2、判断下列说法是否正确:
(1)延长射线OA;(2)直线比射线长,射线比线段长;(3)直线AB和直线CD相交于点m;(4)A、B两点间的距离就是连结A、B两点间的线段。3.用一个钉子把一根细木条钉在木板上,用手拔木条,木条能转动,这表明___________ ;用两个钉子把 细木条钉在木板上,就能固定细木条,这说明________________。4.如图所示,一只蚂蚁要从圆柱体A点沿表面尽可能地爬到B点,因为那里有它的食物,而它饿得快不行了,怎么爬行路线最短?··AB过一点有无数条直线两点确定一条直线5.有关线段的计算问题(1)如图,A、B、C、D是直线l上顺次四点,且线段AC=5,BD=4,则线段AB-CD=_____.ABCD l(2)如图,AC=8cm,CB=6cm,如果O是线段AB的中点,求线段OC的长度。ABCO(3)已知AB=16cm,C是AB上一点,且AC=10cm,D为AC的中点,E是BC的中点,求线段DE的长。(4)同一直线上有A、B、C、D四点,已知AD= DB,AC= CB,且CD=4cm,求AB的长。(5)已知线段AC和线段BC在同一直线上,若AC=5.6cm,BC=2.4cm.求线段AC的中点与线段BC中点之间的距离。探究一、有关距离问题1.如图,在一条笔直的公路a两侧,分别有A、B两个村庄,现要在公路a上建一个汽车站C,使汽车站到A、B两村距离之和最小,问汽车站C的位置应该如何确定?aAB··2.平原上有A、B、C、D四个村庄,如图所示,为解决当地缺水问题,政府准备投资修建一个蓄水池,不考虑其他因素,请你画图确定蓄水池H的位置,使它与四个村庄的距离之和最小.····ABCD3.如图,蚂蚁在圆锥底边的点A处,它想绕圆锥爬行一周后回到点A处,你能画出它爬行的最短路线吗?A(4).如图所示,洋河酒厂有三个住宅区A、B、C各分别住有职工30人、15人、10人,且这三个区在酒家大道上(A、B、C)三点共线,已知AB=100米,BC=200米.为了方便职工上下班,该厂的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在_____区.ABC探究二:画一画,数一数,再找规律1.在平面内有n个点(n≥3),其中没有任何三个点在一条直线上,如果过任意两点画一条直线,这n个点可以画多少条直线?2.一条直线将平面分成两部分,两条直线将平面分成四部分,那么三条直线将平面 最多分成几部分?四条直线将平面最多分成几部分?n条直线呢?4.2线段的长短比较1 度量法2 叠合法3 线段中点的定义和简单作法。直线、射线、线段的比较二、直线、 射线、 线段1.直线、射线、线段的区别和联系
(1,)射线、线段都是直线的一部分,它们之间又有紧密的
联系;在直线上取一点,可以将该直线分成两条射线,取
两点可以得到一条线段和四条射线;把射线反向延长或
者把线段两方延长就可以得到直线。
(2.) 列表比较有关概念点、线段、射线、直线
* 线和线相交的地方是点(point)。
* 点通常表示一个物体的位置。例如,在交通图上用点来表示城市的位置。
* 直线上两个点和它们之间的部分叫做线段(line segment),这两个点叫做线段的端点。
在日常生活中,一根拉紧的绳子、一根竹竿、人行横道线都给我们以线段的形象。
* 把线段向一方无限延伸所形成的图形叫做射线(ray)。
* 把线段向两方无限延伸所形成的图形叫做直线
(straight line)。
(2)线段的中点
把一条线段分成两条相等线段的点,叫做这条线段的中点(middle point)。
2.线段的大小和比较
(1)线段的长短比较度量法叠合法AB=BC=ACAC=2AB=2BC例如:点B是线段AC的中点. . .ABC则有:(3)线段的三等分点
把一条线段分成三条相等线段的两个点,叫做这条线段的三等分点。. . . .A B C DAB=BC=CD=ADAD=3AB=3BC=3CD(4)画一条线段等于已知线段
注意耶用尺规作图法(5)两点的距离与线段的区别
两点的距离是指连接两点间的线段的长度,是一个数量;
而线段本身是图形.(6)线段的和、差
a.线段的和A B C. . .AC=AB+BCb.线段的差M N P. . .MN=MP-NPNP=MP-MN 例4 已知∠α和∠β互为补角,并且∠β的一半比∠α小30o,求∠α、∠β. 解:设∠α=xo,则∠β=180o-xo.根据题意 ∠β=2(∠α-30o),得 180- x=2(x -30),解得 x=80.所以 ,∠α=80o,∠β=100o. 例3 点A,B,C 在同一条直线上,
AB=3 cm,BC=1 cm.求AC的长.解:(1)如图①,因AB=3 ,BC=1,
所以,AC=AB+BC=3+1=4(cm).
(2)如图②,因AB=3,BC=1,
所以AC=AB-BC=3-1=2(cm).
同课章节目录
