26.2.2实际问题与反比例函数 课件
图片预览











文档简介
课件37张PPT。 寒假到了,小迪正与几个同伴在结冰的河面上溜冰,突然发现前面有一处冰出现了裂痕,小迪立即告诉同伴分散趴在冰面上,匍匐离开了危险区. 某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全迅速通过这片湿地,他们沿着前进路线铺垫了若干木板,构筑了一条临时通道,从而顺利完成了任务.问题1: 你能解释他们这样做的道理吗? 问题2:当人的身体或木板对地面的压力一定时,随着与地面接触面积S(m2)的变化,人的身体或木板对地面的压强P(Pa)将如何变化?主要是为减小压强而安全通过. 由P=F/S可知,当压力一定时,随着人或木板面积的增大,人和木板对地面的压强减小.26.2.2实际问题与反比例函数课件
利用反比例函数的知识,分析、解决实际问题.渗透数形结合思想,提高用函数观点解决问题的能力.
进一步提高用函数观点解决问题的能力,体会和认识反比例函数这一数学模型.渗透数形结合思想.
渗透数形结合思想,进一步提高用函数观点解决问题的能力,体会和认识反比例函数这一数学模型.利用反比例函数的知识分析、解决实际问题.
分析实际问题中的数量关系,正确写出函数解析式. 压强是物体单位面积受到的压力.
同一压力作用在支承物的表面上,若受力面积不同,所产生的压强大小也有所不同.受力面积小时,压强大;受力面积大时,压强小.例1 压强问题 某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全迅速通过这片湿地,他们沿着前进路线铺垫了若干木板,构筑了一条临时通道,从而顺利完成了任务.你能解释他们这样做的道理吗?当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强P(Pa)将如何变化? 如果人和木板对湿地地面的压力合计600N,那么(1)用含S的代数式表示P,P是S的反比例函数吗?为什么?(2)当木板面积为0.2m2时,压强是多少?解:当S=0.2m2时,P=600/0.2=3000(Pa)所以,P是S的反比例函数. (3)如果要求压强不超过6000Pa,木板面积至少要多大? 解:当P≤6000时,S≥600/6000=0.1(m2)
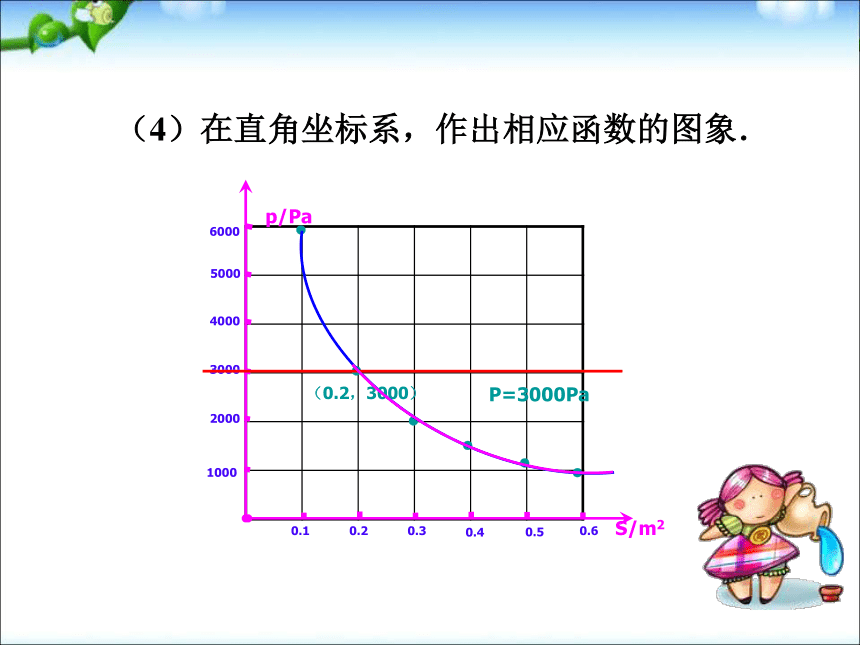
所以木板面积至少要0.1m2.(4)在直角坐标系,作出相应函数的图象.0.1100040003000500060000.20.30.40.50.62000●●●●●●你认为这可能吗?为什么?例2 杠杆问题 阻力×阻力臂=动力×动力臂阻力臂阻力动力臂动力杠杆定律 几位同学玩撬石头的游戏,已知阻力和阻力臂不变,分别是1200牛顿和0.5米,设动力为F,动力臂为L.回答下列问题:(1)动力F与动力臂L有怎样的函数关系?解:(1)由已知得F×L=1200×0.5变形得:动力臂越长就越省力. (2)小松、小冰、小宁、小力分别选取了动力臂为1米、1.5米、2米、4米的撬棍,你能得出他们各自撬动石头至少需要多大的力吗? (3)假定地球重量的近似值为6×1025牛顿即为阻力),假设阿基米德有500牛顿的力量,阻力臂为2000千米,请你帮助阿基米德设计该用多长动力臂的杠杆才能把地球撬动.给我一个支点我可以撬动整个地球.解:由已知得F×L=6×1025×2×106=1.2×1032变形得:当F=500时,L=2.4×1029米 1.在某一电路中,保持电压不变,电流I(安培)和电阻(欧姆)成反比例,当电阻R=8欧姆时,电流I=1.5安培.
(1)求I与R之间的函数关系式;
(2)当电流I=2时,求电阻R的值.解:(1)U=IR=1.5×8=12V例3 电阻问题 (2)用电器输出功率的范围多大? 2.一个用电器的电阻是可调节的,其范围为110~220欧姆.已知电压为220伏,这个用电器的电路图如图所示.(1)输出功率P与电阻R有怎样的函数关系? 解:(1)输出功率P与电阻R呈反比例,它们的函数关系为(2)从(1)式可以看出,电阻越大则功率越小.把电阻的最大值R=220代入①式,则得到输出功率的最小值因此,用电器的输出功率在220瓦到440瓦之间.把电阻的最小值R=110代入①式,得到输出功率最大值: 码头工人以每天30吨的速度往一艘轮船上装载货物,把轮船装载完毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?例4 速度与时间问题 (2)由于遇到紧急情况,船上的货物必须在不超过5日内写在完毕,那么平均每天要卸多少吨货物? 解:(1)设轮船上的货物总量为k吨,则根据已知条件有 所以v与t的函数式为 从结果可以看出,如果全部货物恰好用5天卸完,则平均每天卸载48吨.若货物在不超过5天内卸完,则平均每天至少要卸货48吨. 1.某蓄水池的排水管每时排水8m3,6h可将满池水全部排空. (2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化?(3)写出t与Q之间的函数关系式? (5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空? (4)如果准备在5h内将满池水排空,那么每时的排水量至少为多少?(1)蓄水池的容积是多少?例5 排水问题 解:(1)蓄水池的容积为:8×6=48(m3).(2)此时所需时间t(h)将减少. (4)当t=5h时,Q=48/5=9.6m3.所以每时的排水量至少为9.6m3. (5)当Q=12(m3)时,t=48/12=4(h), 所以最少需5h可将满池水全部排空. 1.(浙江)为了预防“非典”,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例,现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg.请根据题中所提供的信息,解答下列问题: (2)药物燃烧完后,y与x的关系式为__________________; (1)药物燃烧时,y与x的关系式为____________________; O5 用函数观点解实际问题的关键:
一要搞清题目中的基本数量关系,将实际问题抽象成数学问题,看看各变量间应满足什么样的关系式;
二是要分清自变量和函数,以便写出正确的函数关系式,并注意自变量的取值范围;
三要熟练掌握反比例函数的意义、图象和性质,特别是图象,要做到数形结合,这样有利于分析和解决问题.1.京沈高速公路全长658km,汽车沿京沈高速
公路从沈阳驶往北京,则汽车行完全程所需
时间t(h)与行驶的平均速度v(km/h)之
间的函数关系式是_________________.2.某工作小组完成某项任务可获得2000元报酬,
若计划由x人完成这项任务,则人均报酬y
(元)与人数x(人)之间的函数关系式是
__________ .3.小伟欲用撬棍撬动一块大石头,已知阻力和
阻力臂不变,分别为1200牛顿和0.5米.
(1)动力F与动力臂l有怎样的函数关系?当
动力臂为1.5米时,撬动石头至少需要多大的
力?
(2)若想使动力F不超过题(1)中所用的一
半,则动力臂至少要加长多少? 解:(1)根据“杠杆定律”有
得函数关系式
当l=1.5时
因此撬动石头至少需要400牛顿的力.
(2)根据上题可知:Fl=600
得函数关系式
当 时
3-1.5=1.5(米)
因此,若想用力不超过400牛顿的一半,则动力臂至少要加长1.5米.4. 如图所示,某搬运工要撬动一石头,已知阻力为1000N,阻力臂长为5cm.设动力y(N),动力臂为x(cm)(动力×动力臂=阻力×阻力臂)
(1)求y关于x的函数解析式.这个函数是反比例函数吗?如果是,请说出比例系数;是反比例函数,比例系数是5000 (2)求当x=50时,函数y的值,并说明这个值的实际意义: (3)利用y关于x的函数解析式,说明当动力臂长扩大到原来的n倍时,所需动力将怎样变化?y的值是100,说明动力臂越长越省力.5.小眉将一篇30 000字的社会调查报告录入电
脑,打印成文.
(1)如果小眉以每分种200字的速度录入,
他需要多少时间才能完成录入任务.
(2)录入文字的速度v(字/min)与完成录
入的时间t(min)有怎样的函数关系?
(3)若小眉计划在4h内完成录入任务,那么
她每分钟至少应录入多少个字?150分钟125个字6.如图,某玻璃器皿制造公司要制造一种容积
为1升(1升=1立方分米)的圆锥形漏斗.
(1)漏斗口的面积S与漏斗的深d有怎样的函
数关系?
(2)如果漏斗口的面积为100厘米2,则漏斗的
深为多少?(2)30cm.7.已知:A是双曲线上的一点,过点A向x轴
作垂线,垂足为B,△AOB的面积是4,则
它的解析式为 . 2. (1)
(2)2×103 和 103
,250
5. (1) (2)1.1kg/m3
6. (1) (2)4天内 (3)60人
7. (1) (2)不够,至少还需要加20升.课件37张PPT。 寒假到了,小迪正与几个同伴在结冰的河面上溜冰,突然发现前面有一处冰出现了裂痕,小迪立即告诉同伴分散趴在冰面上,匍匐离开了危险区. 某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全迅速通过这片湿地,他们沿着前进路线铺垫了若干木板,构筑了一条临时通道,从而顺利完成了任务.问题1: 你能解释他们这样做的道理吗? 问题2:当人的身体或木板对地面的压力一定时,随着与地面接触面积S(m2)的变化,人的身体或木板对地面的压强P(Pa)将如何变化?主要是为减小压强而安全通过. 由P=F/S可知,当压力一定时,随着人或木板面积的增大,人和木板对地面的压强减小.26.2.2实际问题与反比例函数课件
利用反比例函数的知识,分析、解决实际问题.渗透数形结合思想,提高用函数观点解决问题的能力.
进一步提高用函数观点解决问题的能力,体会和认识反比例函数这一数学模型.渗透数形结合思想.
渗透数形结合思想,进一步提高用函数观点解决问题的能力,体会和认识反比例函数这一数学模型.利用反比例函数的知识分析、解决实际问题.
分析实际问题中的数量关系,正确写出函数解析式. 压强是物体单位面积受到的压力.
同一压力作用在支承物的表面上,若受力面积不同,所产生的压强大小也有所不同.受力面积小时,压强大;受力面积大时,压强小.例1 压强问题 某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全迅速通过这片湿地,他们沿着前进路线铺垫了若干木板,构筑了一条临时通道,从而顺利完成了任务.你能解释他们这样做的道理吗?当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强P(Pa)将如何变化? 如果人和木板对湿地地面的压力合计600N,那么(1)用含S的代数式表示P,P是S的反比例函数吗?为什么?(2)当木板面积为0.2m2时,压强是多少?解:当S=0.2m2时,P=600/0.2=3000(Pa)所以,P是S的反比例函数. (3)如果要求压强不超过6000Pa,木板面积至少要多大? 解:当P≤6000时,S≥600/6000=0.1(m2)
所以木板面积至少要0.1m2.(4)在直角坐标系,作出相应函数的图象.0.1100040003000500060000.20.30.40.50.62000●●●●●●你认为这可能吗?为什么?例2 杠杆问题 阻力×阻力臂=动力×动力臂阻力臂阻力动力臂动力杠杆定律 几位同学玩撬石头的游戏,已知阻力和阻力臂不变,分别是1200牛顿和0.5米,设动力为F,动力臂为L.回答下列问题:(1)动力F与动力臂L有怎样的函数关系?解:(1)由已知得F×L=1200×0.5变形得:动力臂越长就越省力. (2)小松、小冰、小宁、小力分别选取了动力臂为1米、1.5米、2米、4米的撬棍,你能得出他们各自撬动石头至少需要多大的力吗? (3)假定地球重量的近似值为6×1025牛顿即为阻力),假设阿基米德有500牛顿的力量,阻力臂为2000千米,请你帮助阿基米德设计该用多长动力臂的杠杆才能把地球撬动.给我一个支点我可以撬动整个地球.解:由已知得F×L=6×1025×2×106=1.2×1032变形得:当F=500时,L=2.4×1029米 1.在某一电路中,保持电压不变,电流I(安培)和电阻(欧姆)成反比例,当电阻R=8欧姆时,电流I=1.5安培.
(1)求I与R之间的函数关系式;
(2)当电流I=2时,求电阻R的值.解:(1)U=IR=1.5×8=12V例3 电阻问题 (2)用电器输出功率的范围多大? 2.一个用电器的电阻是可调节的,其范围为110~220欧姆.已知电压为220伏,这个用电器的电路图如图所示.(1)输出功率P与电阻R有怎样的函数关系? 解:(1)输出功率P与电阻R呈反比例,它们的函数关系为(2)从(1)式可以看出,电阻越大则功率越小.把电阻的最大值R=220代入①式,则得到输出功率的最小值因此,用电器的输出功率在220瓦到440瓦之间.把电阻的最小值R=110代入①式,得到输出功率最大值: 码头工人以每天30吨的速度往一艘轮船上装载货物,把轮船装载完毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?例4 速度与时间问题 (2)由于遇到紧急情况,船上的货物必须在不超过5日内写在完毕,那么平均每天要卸多少吨货物? 解:(1)设轮船上的货物总量为k吨,则根据已知条件有 所以v与t的函数式为 从结果可以看出,如果全部货物恰好用5天卸完,则平均每天卸载48吨.若货物在不超过5天内卸完,则平均每天至少要卸货48吨. 1.某蓄水池的排水管每时排水8m3,6h可将满池水全部排空. (2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化?(3)写出t与Q之间的函数关系式? (5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空? (4)如果准备在5h内将满池水排空,那么每时的排水量至少为多少?(1)蓄水池的容积是多少?例5 排水问题 解:(1)蓄水池的容积为:8×6=48(m3).(2)此时所需时间t(h)将减少. (4)当t=5h时,Q=48/5=9.6m3.所以每时的排水量至少为9.6m3. (5)当Q=12(m3)时,t=48/12=4(h), 所以最少需5h可将满池水全部排空. 1.(浙江)为了预防“非典”,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例,现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg.请根据题中所提供的信息,解答下列问题: (2)药物燃烧完后,y与x的关系式为__________________; (1)药物燃烧时,y与x的关系式为____________________; O5 用函数观点解实际问题的关键:
一要搞清题目中的基本数量关系,将实际问题抽象成数学问题,看看各变量间应满足什么样的关系式;
二是要分清自变量和函数,以便写出正确的函数关系式,并注意自变量的取值范围;
三要熟练掌握反比例函数的意义、图象和性质,特别是图象,要做到数形结合,这样有利于分析和解决问题.1.京沈高速公路全长658km,汽车沿京沈高速
公路从沈阳驶往北京,则汽车行完全程所需
时间t(h)与行驶的平均速度v(km/h)之
间的函数关系式是_________________.2.某工作小组完成某项任务可获得2000元报酬,
若计划由x人完成这项任务,则人均报酬y
(元)与人数x(人)之间的函数关系式是
__________ .3.小伟欲用撬棍撬动一块大石头,已知阻力和
阻力臂不变,分别为1200牛顿和0.5米.
(1)动力F与动力臂l有怎样的函数关系?当
动力臂为1.5米时,撬动石头至少需要多大的
力?
(2)若想使动力F不超过题(1)中所用的一
半,则动力臂至少要加长多少? 解:(1)根据“杠杆定律”有
得函数关系式
当l=1.5时
因此撬动石头至少需要400牛顿的力.
(2)根据上题可知:Fl=600
得函数关系式
当 时
3-1.5=1.5(米)
因此,若想用力不超过400牛顿的一半,则动力臂至少要加长1.5米.4. 如图所示,某搬运工要撬动一石头,已知阻力为1000N,阻力臂长为5cm.设动力y(N),动力臂为x(cm)(动力×动力臂=阻力×阻力臂)
(1)求y关于x的函数解析式.这个函数是反比例函数吗?如果是,请说出比例系数;是反比例函数,比例系数是5000 (2)求当x=50时,函数y的值,并说明这个值的实际意义: (3)利用y关于x的函数解析式,说明当动力臂长扩大到原来的n倍时,所需动力将怎样变化?y的值是100,说明动力臂越长越省力.5.小眉将一篇30 000字的社会调查报告录入电
脑,打印成文.
(1)如果小眉以每分种200字的速度录入,
他需要多少时间才能完成录入任务.
(2)录入文字的速度v(字/min)与完成录
入的时间t(min)有怎样的函数关系?
(3)若小眉计划在4h内完成录入任务,那么
她每分钟至少应录入多少个字?150分钟125个字6.如图,某玻璃器皿制造公司要制造一种容积
为1升(1升=1立方分米)的圆锥形漏斗.
(1)漏斗口的面积S与漏斗的深d有怎样的函
数关系?
(2)如果漏斗口的面积为100厘米2,则漏斗的
深为多少?(2)30cm.7.已知:A是双曲线上的一点,过点A向x轴
作垂线,垂足为B,△AOB的面积是4,则
它的解析式为 . 2. (1)
(2)2×103 和 103
,250
5. (1) (2)1.1kg/m3
6. (1) (2)4天内 (3)60人
7. (1) (2)不够,至少还需要加20升.
利用反比例函数的知识,分析、解决实际问题.渗透数形结合思想,提高用函数观点解决问题的能力.
进一步提高用函数观点解决问题的能力,体会和认识反比例函数这一数学模型.渗透数形结合思想.
渗透数形结合思想,进一步提高用函数观点解决问题的能力,体会和认识反比例函数这一数学模型.利用反比例函数的知识分析、解决实际问题.
分析实际问题中的数量关系,正确写出函数解析式. 压强是物体单位面积受到的压力.
同一压力作用在支承物的表面上,若受力面积不同,所产生的压强大小也有所不同.受力面积小时,压强大;受力面积大时,压强小.例1 压强问题 某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全迅速通过这片湿地,他们沿着前进路线铺垫了若干木板,构筑了一条临时通道,从而顺利完成了任务.你能解释他们这样做的道理吗?当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强P(Pa)将如何变化? 如果人和木板对湿地地面的压力合计600N,那么(1)用含S的代数式表示P,P是S的反比例函数吗?为什么?(2)当木板面积为0.2m2时,压强是多少?解:当S=0.2m2时,P=600/0.2=3000(Pa)所以,P是S的反比例函数. (3)如果要求压强不超过6000Pa,木板面积至少要多大? 解:当P≤6000时,S≥600/6000=0.1(m2)
所以木板面积至少要0.1m2.(4)在直角坐标系,作出相应函数的图象.0.1100040003000500060000.20.30.40.50.62000●●●●●●你认为这可能吗?为什么?例2 杠杆问题 阻力×阻力臂=动力×动力臂阻力臂阻力动力臂动力杠杆定律 几位同学玩撬石头的游戏,已知阻力和阻力臂不变,分别是1200牛顿和0.5米,设动力为F,动力臂为L.回答下列问题:(1)动力F与动力臂L有怎样的函数关系?解:(1)由已知得F×L=1200×0.5变形得:动力臂越长就越省力. (2)小松、小冰、小宁、小力分别选取了动力臂为1米、1.5米、2米、4米的撬棍,你能得出他们各自撬动石头至少需要多大的力吗? (3)假定地球重量的近似值为6×1025牛顿即为阻力),假设阿基米德有500牛顿的力量,阻力臂为2000千米,请你帮助阿基米德设计该用多长动力臂的杠杆才能把地球撬动.给我一个支点我可以撬动整个地球.解:由已知得F×L=6×1025×2×106=1.2×1032变形得:当F=500时,L=2.4×1029米 1.在某一电路中,保持电压不变,电流I(安培)和电阻(欧姆)成反比例,当电阻R=8欧姆时,电流I=1.5安培.
(1)求I与R之间的函数关系式;
(2)当电流I=2时,求电阻R的值.解:(1)U=IR=1.5×8=12V例3 电阻问题 (2)用电器输出功率的范围多大? 2.一个用电器的电阻是可调节的,其范围为110~220欧姆.已知电压为220伏,这个用电器的电路图如图所示.(1)输出功率P与电阻R有怎样的函数关系? 解:(1)输出功率P与电阻R呈反比例,它们的函数关系为(2)从(1)式可以看出,电阻越大则功率越小.把电阻的最大值R=220代入①式,则得到输出功率的最小值因此,用电器的输出功率在220瓦到440瓦之间.把电阻的最小值R=110代入①式,得到输出功率最大值: 码头工人以每天30吨的速度往一艘轮船上装载货物,把轮船装载完毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?例4 速度与时间问题 (2)由于遇到紧急情况,船上的货物必须在不超过5日内写在完毕,那么平均每天要卸多少吨货物? 解:(1)设轮船上的货物总量为k吨,则根据已知条件有 所以v与t的函数式为 从结果可以看出,如果全部货物恰好用5天卸完,则平均每天卸载48吨.若货物在不超过5天内卸完,则平均每天至少要卸货48吨. 1.某蓄水池的排水管每时排水8m3,6h可将满池水全部排空. (2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化?(3)写出t与Q之间的函数关系式? (5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空? (4)如果准备在5h内将满池水排空,那么每时的排水量至少为多少?(1)蓄水池的容积是多少?例5 排水问题 解:(1)蓄水池的容积为:8×6=48(m3).(2)此时所需时间t(h)将减少. (4)当t=5h时,Q=48/5=9.6m3.所以每时的排水量至少为9.6m3. (5)当Q=12(m3)时,t=48/12=4(h), 所以最少需5h可将满池水全部排空. 1.(浙江)为了预防“非典”,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例,现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg.请根据题中所提供的信息,解答下列问题: (2)药物燃烧完后,y与x的关系式为__________________; (1)药物燃烧时,y与x的关系式为____________________; O5 用函数观点解实际问题的关键:
一要搞清题目中的基本数量关系,将实际问题抽象成数学问题,看看各变量间应满足什么样的关系式;
二是要分清自变量和函数,以便写出正确的函数关系式,并注意自变量的取值范围;
三要熟练掌握反比例函数的意义、图象和性质,特别是图象,要做到数形结合,这样有利于分析和解决问题.1.京沈高速公路全长658km,汽车沿京沈高速
公路从沈阳驶往北京,则汽车行完全程所需
时间t(h)与行驶的平均速度v(km/h)之
间的函数关系式是_________________.2.某工作小组完成某项任务可获得2000元报酬,
若计划由x人完成这项任务,则人均报酬y
(元)与人数x(人)之间的函数关系式是
__________ .3.小伟欲用撬棍撬动一块大石头,已知阻力和
阻力臂不变,分别为1200牛顿和0.5米.
(1)动力F与动力臂l有怎样的函数关系?当
动力臂为1.5米时,撬动石头至少需要多大的
力?
(2)若想使动力F不超过题(1)中所用的一
半,则动力臂至少要加长多少? 解:(1)根据“杠杆定律”有
得函数关系式
当l=1.5时
因此撬动石头至少需要400牛顿的力.
(2)根据上题可知:Fl=600
得函数关系式
当 时
3-1.5=1.5(米)
因此,若想用力不超过400牛顿的一半,则动力臂至少要加长1.5米.4. 如图所示,某搬运工要撬动一石头,已知阻力为1000N,阻力臂长为5cm.设动力y(N),动力臂为x(cm)(动力×动力臂=阻力×阻力臂)
(1)求y关于x的函数解析式.这个函数是反比例函数吗?如果是,请说出比例系数;是反比例函数,比例系数是5000 (2)求当x=50时,函数y的值,并说明这个值的实际意义: (3)利用y关于x的函数解析式,说明当动力臂长扩大到原来的n倍时,所需动力将怎样变化?y的值是100,说明动力臂越长越省力.5.小眉将一篇30 000字的社会调查报告录入电
脑,打印成文.
(1)如果小眉以每分种200字的速度录入,
他需要多少时间才能完成录入任务.
(2)录入文字的速度v(字/min)与完成录
入的时间t(min)有怎样的函数关系?
(3)若小眉计划在4h内完成录入任务,那么
她每分钟至少应录入多少个字?150分钟125个字6.如图,某玻璃器皿制造公司要制造一种容积
为1升(1升=1立方分米)的圆锥形漏斗.
(1)漏斗口的面积S与漏斗的深d有怎样的函
数关系?
(2)如果漏斗口的面积为100厘米2,则漏斗的
深为多少?(2)30cm.7.已知:A是双曲线上的一点,过点A向x轴
作垂线,垂足为B,△AOB的面积是4,则
它的解析式为 . 2. (1)
(2)2×103 和 103
,250
5. (1) (2)1.1kg/m3
6. (1) (2)4天内 (3)60人
7. (1) (2)不够,至少还需要加20升.课件37张PPT。 寒假到了,小迪正与几个同伴在结冰的河面上溜冰,突然发现前面有一处冰出现了裂痕,小迪立即告诉同伴分散趴在冰面上,匍匐离开了危险区. 某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全迅速通过这片湿地,他们沿着前进路线铺垫了若干木板,构筑了一条临时通道,从而顺利完成了任务.问题1: 你能解释他们这样做的道理吗? 问题2:当人的身体或木板对地面的压力一定时,随着与地面接触面积S(m2)的变化,人的身体或木板对地面的压强P(Pa)将如何变化?主要是为减小压强而安全通过. 由P=F/S可知,当压力一定时,随着人或木板面积的增大,人和木板对地面的压强减小.26.2.2实际问题与反比例函数课件
利用反比例函数的知识,分析、解决实际问题.渗透数形结合思想,提高用函数观点解决问题的能力.
进一步提高用函数观点解决问题的能力,体会和认识反比例函数这一数学模型.渗透数形结合思想.
渗透数形结合思想,进一步提高用函数观点解决问题的能力,体会和认识反比例函数这一数学模型.利用反比例函数的知识分析、解决实际问题.
分析实际问题中的数量关系,正确写出函数解析式. 压强是物体单位面积受到的压力.
同一压力作用在支承物的表面上,若受力面积不同,所产生的压强大小也有所不同.受力面积小时,压强大;受力面积大时,压强小.例1 压强问题 某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全迅速通过这片湿地,他们沿着前进路线铺垫了若干木板,构筑了一条临时通道,从而顺利完成了任务.你能解释他们这样做的道理吗?当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强P(Pa)将如何变化? 如果人和木板对湿地地面的压力合计600N,那么(1)用含S的代数式表示P,P是S的反比例函数吗?为什么?(2)当木板面积为0.2m2时,压强是多少?解:当S=0.2m2时,P=600/0.2=3000(Pa)所以,P是S的反比例函数. (3)如果要求压强不超过6000Pa,木板面积至少要多大? 解:当P≤6000时,S≥600/6000=0.1(m2)
所以木板面积至少要0.1m2.(4)在直角坐标系,作出相应函数的图象.0.1100040003000500060000.20.30.40.50.62000●●●●●●你认为这可能吗?为什么?例2 杠杆问题 阻力×阻力臂=动力×动力臂阻力臂阻力动力臂动力杠杆定律 几位同学玩撬石头的游戏,已知阻力和阻力臂不变,分别是1200牛顿和0.5米,设动力为F,动力臂为L.回答下列问题:(1)动力F与动力臂L有怎样的函数关系?解:(1)由已知得F×L=1200×0.5变形得:动力臂越长就越省力. (2)小松、小冰、小宁、小力分别选取了动力臂为1米、1.5米、2米、4米的撬棍,你能得出他们各自撬动石头至少需要多大的力吗? (3)假定地球重量的近似值为6×1025牛顿即为阻力),假设阿基米德有500牛顿的力量,阻力臂为2000千米,请你帮助阿基米德设计该用多长动力臂的杠杆才能把地球撬动.给我一个支点我可以撬动整个地球.解:由已知得F×L=6×1025×2×106=1.2×1032变形得:当F=500时,L=2.4×1029米 1.在某一电路中,保持电压不变,电流I(安培)和电阻(欧姆)成反比例,当电阻R=8欧姆时,电流I=1.5安培.
(1)求I与R之间的函数关系式;
(2)当电流I=2时,求电阻R的值.解:(1)U=IR=1.5×8=12V例3 电阻问题 (2)用电器输出功率的范围多大? 2.一个用电器的电阻是可调节的,其范围为110~220欧姆.已知电压为220伏,这个用电器的电路图如图所示.(1)输出功率P与电阻R有怎样的函数关系? 解:(1)输出功率P与电阻R呈反比例,它们的函数关系为(2)从(1)式可以看出,电阻越大则功率越小.把电阻的最大值R=220代入①式,则得到输出功率的最小值因此,用电器的输出功率在220瓦到440瓦之间.把电阻的最小值R=110代入①式,得到输出功率最大值: 码头工人以每天30吨的速度往一艘轮船上装载货物,把轮船装载完毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?例4 速度与时间问题 (2)由于遇到紧急情况,船上的货物必须在不超过5日内写在完毕,那么平均每天要卸多少吨货物? 解:(1)设轮船上的货物总量为k吨,则根据已知条件有 所以v与t的函数式为 从结果可以看出,如果全部货物恰好用5天卸完,则平均每天卸载48吨.若货物在不超过5天内卸完,则平均每天至少要卸货48吨. 1.某蓄水池的排水管每时排水8m3,6h可将满池水全部排空. (2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化?(3)写出t与Q之间的函数关系式? (5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空? (4)如果准备在5h内将满池水排空,那么每时的排水量至少为多少?(1)蓄水池的容积是多少?例5 排水问题 解:(1)蓄水池的容积为:8×6=48(m3).(2)此时所需时间t(h)将减少. (4)当t=5h时,Q=48/5=9.6m3.所以每时的排水量至少为9.6m3. (5)当Q=12(m3)时,t=48/12=4(h), 所以最少需5h可将满池水全部排空. 1.(浙江)为了预防“非典”,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例,现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg.请根据题中所提供的信息,解答下列问题: (2)药物燃烧完后,y与x的关系式为__________________; (1)药物燃烧时,y与x的关系式为____________________; O5 用函数观点解实际问题的关键:
一要搞清题目中的基本数量关系,将实际问题抽象成数学问题,看看各变量间应满足什么样的关系式;
二是要分清自变量和函数,以便写出正确的函数关系式,并注意自变量的取值范围;
三要熟练掌握反比例函数的意义、图象和性质,特别是图象,要做到数形结合,这样有利于分析和解决问题.1.京沈高速公路全长658km,汽车沿京沈高速
公路从沈阳驶往北京,则汽车行完全程所需
时间t(h)与行驶的平均速度v(km/h)之
间的函数关系式是_________________.2.某工作小组完成某项任务可获得2000元报酬,
若计划由x人完成这项任务,则人均报酬y
(元)与人数x(人)之间的函数关系式是
__________ .3.小伟欲用撬棍撬动一块大石头,已知阻力和
阻力臂不变,分别为1200牛顿和0.5米.
(1)动力F与动力臂l有怎样的函数关系?当
动力臂为1.5米时,撬动石头至少需要多大的
力?
(2)若想使动力F不超过题(1)中所用的一
半,则动力臂至少要加长多少? 解:(1)根据“杠杆定律”有
得函数关系式
当l=1.5时
因此撬动石头至少需要400牛顿的力.
(2)根据上题可知:Fl=600
得函数关系式
当 时
3-1.5=1.5(米)
因此,若想用力不超过400牛顿的一半,则动力臂至少要加长1.5米.4. 如图所示,某搬运工要撬动一石头,已知阻力为1000N,阻力臂长为5cm.设动力y(N),动力臂为x(cm)(动力×动力臂=阻力×阻力臂)
(1)求y关于x的函数解析式.这个函数是反比例函数吗?如果是,请说出比例系数;是反比例函数,比例系数是5000 (2)求当x=50时,函数y的值,并说明这个值的实际意义: (3)利用y关于x的函数解析式,说明当动力臂长扩大到原来的n倍时,所需动力将怎样变化?y的值是100,说明动力臂越长越省力.5.小眉将一篇30 000字的社会调查报告录入电
脑,打印成文.
(1)如果小眉以每分种200字的速度录入,
他需要多少时间才能完成录入任务.
(2)录入文字的速度v(字/min)与完成录
入的时间t(min)有怎样的函数关系?
(3)若小眉计划在4h内完成录入任务,那么
她每分钟至少应录入多少个字?150分钟125个字6.如图,某玻璃器皿制造公司要制造一种容积
为1升(1升=1立方分米)的圆锥形漏斗.
(1)漏斗口的面积S与漏斗的深d有怎样的函
数关系?
(2)如果漏斗口的面积为100厘米2,则漏斗的
深为多少?(2)30cm.7.已知:A是双曲线上的一点,过点A向x轴
作垂线,垂足为B,△AOB的面积是4,则
它的解析式为 . 2. (1)
(2)2×103 和 103
,250
5. (1) (2)1.1kg/m3
6. (1) (2)4天内 (3)60人
7. (1) (2)不够,至少还需要加20升.
