26.1.2反比例函数的图像与性质 课件
图片预览






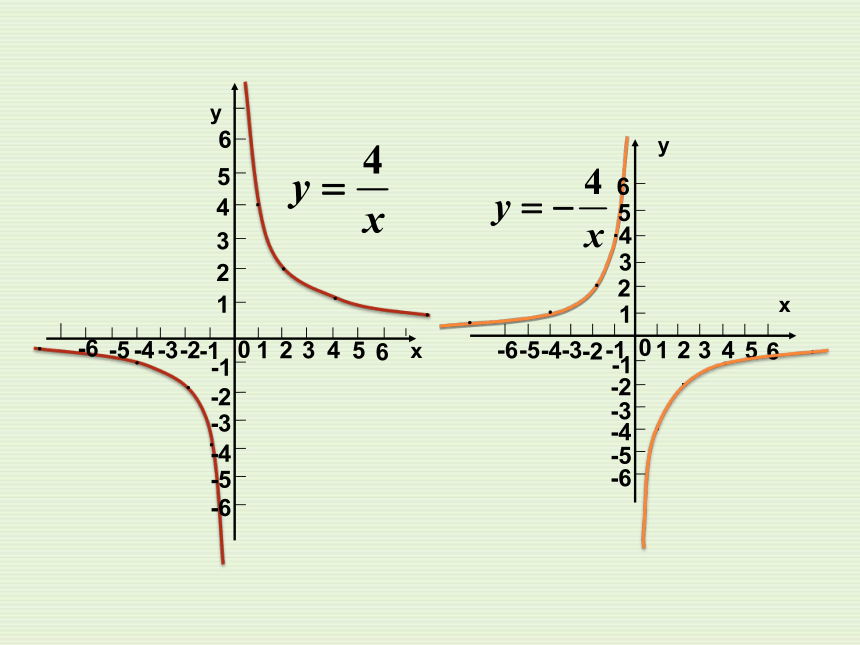

文档简介
课件28张PPT。第二十六章 反比例函数26.1.2反比例函数的
图像和性质 复习提问1. 上节课我们学的反比例函数解析式是什么?
自变量x的取值范围是什么?
函数y的取值范围是什么?x≠0 ,y≠0(k ≠0,k是常数)2、一次函数y=kx+b(k≠0)的图象是什么?3、二次函数y=ax2+bx+c(k≠0)的图象是什么?一条直线抛物线反比例函数 (k≠0)的图象是什么呢?让我们一起画个反比例函数的图象看看,好吗?1、列表2、描点3、连线回忆:画函数图象的一般步骤(怎么列?自变量怎样取值?)(这么连?)(怎么描?)光滑,适当延伸,从左至右连探究新知1、在不知道图象的走向的情况下,取点越多越能反映图象的实际情况,但一般取8—12个值为宜2、应注意:
1、自变量x≠0;
2、自变量x的取值要对称
3、自变量x的取值要便于计算和描点1、自变量x需要取多少值?为什么?
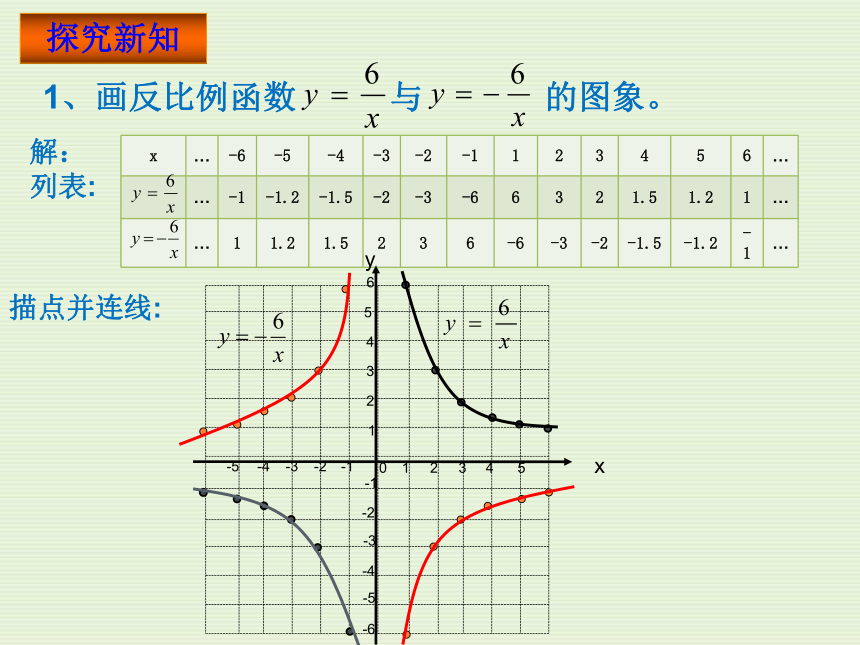
2、取值时要注意什么?描点并连线:12345-1-3-2-4-51234-1-2-3-40-6-556xy解:
列表:探究新知位置:
函数 的两支曲线分别位于第 象限内.
函数 的两支曲线分别位于第 象限内.形状:
反比例函数的图象是由两支曲线组成的.
因此称反比例函数的图象为 .【结论】一、三双曲线二、四你认为作反比例函数图象时应注意哪些问题?1.列表时,选取的自变量的值,既要易于计算,又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线,又可以使图象精确.
2.描点时要严格按照表中所列的对应值描点,绝对不能把点的位置描错.
3.线连时一定要养成按自变量从小到大的顺序依次画线,连线时必须用光滑的曲线连接各点,不能用折线连接.
4.图象是延伸的,注意不要画的有明确端点.
5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交. 议一议:“心动”不如行动探究操作【解析】1.列表:2.描点:3.连线:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.用光滑的曲线顺次连接各点,就可得到图象.123456-4-1-2.-3-5-6124563-6-5-1-3-4-20... yx....xy0132456123456-6-6-5-3-4-1-2-4-5-3-2-1........位置:
函数 的两支曲线分别位于第 象限内.
函数 的两支曲线分别位于第 象限内.形状:
反比例函数的图象是由两支曲线组成的.
因此称反比例函数的图象为 .【结论】一、三双曲线二、四你能画出反比例函数的一般图像吗?(分为k>0和k<0) 当k>0时,在每个象限内y随x的增大而减小;
当k<0时,在每个象限内y
随x的增大而增大; 当k>0时,两支双曲线分别
位于第一,三象限内;
当k<0时,两支双曲线分别
位于第二,四象限内;12345-1-3-2-4-51234-1-2-3-40-55x12345-1-3-2-4-51234-1-2-3-40-55xyy1、这几个函数图象有什么共同点?2、函数图象分别位于哪几个象限?3、y随的x变化有怎样的变化?反比例函数的图象是
由两支曲线组成的.
因此称反比例函数的
图象为双曲线;观察思考4、对称性如何?由两支曲线组成的.因此称它的图象为双曲线;当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.反比例函数的图象无限接近于x,y轴,
但永远不能到达x,y轴既是中心对称,又是轴对称反比例函数的图象和性质形状位置增减性图象的发展趋势对称性归纳发现位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线一三象限 y随x的增大而增大一三象限每一象限内 y随x的增大而减小二四象限二四象限 y随x的增大而减小每一象限内 y随x的增大而增大
正比例函数与反比例函数的区别归纳发现小试牛刀 ( )C小试牛刀3、函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
4、 函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
5、函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三二、四一减小增大减小小试牛刀解得: k=12∴这个反比例函数的表达式为∵k>0∴这个函数的图象在第一、第三象限,
在每个象限内,y随x的增大而减小。∵图象过点A(2,6)例题讲解例题讲解解:(1)反比例函数图象的分布只有两种可能,分布在第一、第三象限,或者分布在第二、第四象限。这个函数的图象的一支在第一象限,则另一支必在第三象限。∵函数的图象在第一、第三象限∴ m-5>0解得 m>5 例题讲解(2)∵m-5>0,在这个函数图象的任一支上,y随x的增大而减小,∴当a>a′时b<b′1、反比例函数的图象如图所示,
则其解析式为 ;B小试牛刀3、已知k<0,则函数 y1=kx, y2=
在同一坐标系中的图象大致是 ( )D小试牛刀y3< y1< y2小试牛刀 5、如图是 三个反比例函数在x轴上方的图像,由此观察得到( )
A、k1>k2>k3 B、k3>k2>k1
C、k2>k1>k3 D、k3>k1>k21k2k3B(m,n)1例题讲解1.如图,点P是反比例函数 图象
上的一点,PA⊥x轴于A, PB⊥y轴于
B.则长方形PAOB的面积为 .2小试牛刀S1S3S2AA.S1 = S2 = S3 B. S1 < S2 < S3
C. S3 < S1 < S2 D. S1 > S2 >S3 1、已知反比例函数
若函数的图象位于第一三象限, 则k______;
若在每一象限内,y随x增大而增大, 则k______.< 4> 42.(江苏南京)反比例函数 (K为常数)图象位于( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限C课堂练习D课堂练习5、若函数 是反比例函数,且图象位于第一、三象限,则m的值为 。m=2课堂练习6、正比例函数y=x与反比例函数 图象交点有 个, 正比例函数y=x与反比例函数 图象交点有 个。204. 已知k>0,则函数 y1=kx+k与
y2= 在同一坐标系中的图
象大致是 ( )C课堂小结谈谈你本节课的收获!1、反比例函数的图象和性质
2、会利用反比例函数图像和性质解决
一些简单的问题巩固提高
图像和性质 复习提问1. 上节课我们学的反比例函数解析式是什么?
自变量x的取值范围是什么?
函数y的取值范围是什么?x≠0 ,y≠0(k ≠0,k是常数)2、一次函数y=kx+b(k≠0)的图象是什么?3、二次函数y=ax2+bx+c(k≠0)的图象是什么?一条直线抛物线反比例函数 (k≠0)的图象是什么呢?让我们一起画个反比例函数的图象看看,好吗?1、列表2、描点3、连线回忆:画函数图象的一般步骤(怎么列?自变量怎样取值?)(这么连?)(怎么描?)光滑,适当延伸,从左至右连探究新知1、在不知道图象的走向的情况下,取点越多越能反映图象的实际情况,但一般取8—12个值为宜2、应注意:
1、自变量x≠0;
2、自变量x的取值要对称
3、自变量x的取值要便于计算和描点1、自变量x需要取多少值?为什么?
2、取值时要注意什么?描点并连线:12345-1-3-2-4-51234-1-2-3-40-6-556xy解:
列表:探究新知位置:
函数 的两支曲线分别位于第 象限内.
函数 的两支曲线分别位于第 象限内.形状:
反比例函数的图象是由两支曲线组成的.
因此称反比例函数的图象为 .【结论】一、三双曲线二、四你认为作反比例函数图象时应注意哪些问题?1.列表时,选取的自变量的值,既要易于计算,又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线,又可以使图象精确.
2.描点时要严格按照表中所列的对应值描点,绝对不能把点的位置描错.
3.线连时一定要养成按自变量从小到大的顺序依次画线,连线时必须用光滑的曲线连接各点,不能用折线连接.
4.图象是延伸的,注意不要画的有明确端点.
5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交. 议一议:“心动”不如行动探究操作【解析】1.列表:2.描点:3.连线:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.用光滑的曲线顺次连接各点,就可得到图象.123456-4-1-2.-3-5-6124563-6-5-1-3-4-20... yx....xy0132456123456-6-6-5-3-4-1-2-4-5-3-2-1........位置:
函数 的两支曲线分别位于第 象限内.
函数 的两支曲线分别位于第 象限内.形状:
反比例函数的图象是由两支曲线组成的.
因此称反比例函数的图象为 .【结论】一、三双曲线二、四你能画出反比例函数的一般图像吗?(分为k>0和k<0) 当k>0时,在每个象限内y随x的增大而减小;
当k<0时,在每个象限内y
随x的增大而增大; 当k>0时,两支双曲线分别
位于第一,三象限内;
当k<0时,两支双曲线分别
位于第二,四象限内;12345-1-3-2-4-51234-1-2-3-40-55x12345-1-3-2-4-51234-1-2-3-40-55xyy1、这几个函数图象有什么共同点?2、函数图象分别位于哪几个象限?3、y随的x变化有怎样的变化?反比例函数的图象是
由两支曲线组成的.
因此称反比例函数的
图象为双曲线;观察思考4、对称性如何?由两支曲线组成的.因此称它的图象为双曲线;当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.反比例函数的图象无限接近于x,y轴,
但永远不能到达x,y轴既是中心对称,又是轴对称反比例函数的图象和性质形状位置增减性图象的发展趋势对称性归纳发现位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线一三象限 y随x的增大而增大一三象限每一象限内 y随x的增大而减小二四象限二四象限 y随x的增大而减小每一象限内 y随x的增大而增大
正比例函数与反比例函数的区别归纳发现小试牛刀 ( )C小试牛刀3、函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
4、 函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
5、函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三二、四一减小增大减小小试牛刀解得: k=12∴这个反比例函数的表达式为∵k>0∴这个函数的图象在第一、第三象限,
在每个象限内,y随x的增大而减小。∵图象过点A(2,6)例题讲解例题讲解解:(1)反比例函数图象的分布只有两种可能,分布在第一、第三象限,或者分布在第二、第四象限。这个函数的图象的一支在第一象限,则另一支必在第三象限。∵函数的图象在第一、第三象限∴ m-5>0解得 m>5 例题讲解(2)∵m-5>0,在这个函数图象的任一支上,y随x的增大而减小,∴当a>a′时b<b′1、反比例函数的图象如图所示,
则其解析式为 ;B小试牛刀3、已知k<0,则函数 y1=kx, y2=
在同一坐标系中的图象大致是 ( )D小试牛刀y3< y1< y2小试牛刀 5、如图是 三个反比例函数在x轴上方的图像,由此观察得到( )
A、k1>k2>k3 B、k3>k2>k1
C、k2>k1>k3 D、k3>k1>k21k2k3B(m,n)1例题讲解1.如图,点P是反比例函数 图象
上的一点,PA⊥x轴于A, PB⊥y轴于
B.则长方形PAOB的面积为 .2小试牛刀S1S3S2AA.S1 = S2 = S3 B. S1 < S2 < S3
C. S3 < S1 < S2 D. S1 > S2 >S3 1、已知反比例函数
若函数的图象位于第一三象限, 则k______;
若在每一象限内,y随x增大而增大, 则k______.< 4> 42.(江苏南京)反比例函数 (K为常数)图象位于( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限C课堂练习D课堂练习5、若函数 是反比例函数,且图象位于第一、三象限,则m的值为 。m=2课堂练习6、正比例函数y=x与反比例函数 图象交点有 个, 正比例函数y=x与反比例函数 图象交点有 个。204. 已知k>0,则函数 y1=kx+k与
y2= 在同一坐标系中的图
象大致是 ( )C课堂小结谈谈你本节课的收获!1、反比例函数的图象和性质
2、会利用反比例函数图像和性质解决
一些简单的问题巩固提高
