山东省聊城市高唐县2017-2018学年九年级数学上学期期中试题(附答案)
文档属性
| 名称 | 山东省聊城市高唐县2017-2018学年九年级数学上学期期中试题(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 330.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-09 23:30:13 | ||
图片预览




文档简介
山东省聊城市高唐县2018届九年级数学上学期期中试题
时间:120分钟;满分:120分
一、选择题(本大题共12小题,共36分)
1、下列方程中,是一元二次方程的是( )
A. 2x-y=3
B. x2+=2
C. x2+1=x2-1
D. x(x-1)=0
2、下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在
格点上,则在网格图中的三角形与△ABC相似的是( )
A.
B.
C.
D.
3、如图,AB是⊙O的直径,CD是弦,∠ABC=65°,则∠D的度数为( )
A. 130°
B. 65°
C. 35°
D. 25°
4、如图,在⊙O中,直径AB与弦CD垂直相交于点E,连结AC,OC,若∠A=30°,OC=4,则弦CD的长是( )
A.
B. 4
C.
D. 8
5、△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC
于D,下列选项中,错误的是( )
A. sinα=cosα
B. tanC=2
C. sinβ=cosβ
D. tanα=1
6、关于x的一元二次方程(m-1)x2+2x+m2-5m+4=0,常数项为0,则m值等于( )
A. 1
B. 4
C. 1或4
D. 0
7、如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
A. 6
B. 8
C. 10
D. 12
8、如图,在△ABC中,点P在边AB上,则在下列四个条件中::①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP?AB;④AB?CP=AP?CB,能满足△APC与△ACB相似的条件是( )
A. ①②④
B. ①③④
C. ②③④
D. ①②③
9、如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
A. 2000米
B. 4000米
C. 2000米
D. (2000+500)米
10、小明同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),则∠APB的度数为( )
A. 45°
B. 135°
C. 45°或135°
D. 90°或135°
11、如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
A. 4或4.8
B. 3或4.8
C. 2或4
D. 1或6
12、如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
A. 16
B. 24-4π
C. 32-4π
D. 32-8π
二、填空题(本大题共5小题,共15分)
13、已知CD是Rt△ABC斜边上的高线,且AB=10,若BC=8,则cos∠ACD= ______ .
14、如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高CD为 米.
15、阅读下面材料: 在数学课上,老师提出如下问题: 尺规作图:作Rt△ABC,使其斜边AB=c,一条直角边BC=a. 已知线段a,c如图. 小芸的作法如下: ① 取AB=c,作AB的垂直平分线交AB于点O; ② 以点O为圆心,OB长为半径画圆; ③ 以点B为圆心,a长为半径画弧,与⊙O交于点C;④ 连接BC,AC. 则Rt△ABC即为所求.老师说:“小芸的作法正确.” 请回答:小芸的作法中判断∠ACB是直角的依据是 .
16、已知一个正六边形的边心距为,则它的半径为______ .
17、如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,…,按此规律继续下去,则矩形ABnCnCn-1的面积为 .
三、解答题
18、计算:(每小题4分,共8分)
(1)sin260°+cos260°-tan45°; (2)|-|+-4cos45°+2sin30°. 19、解方程:(每小题4分,共8分)
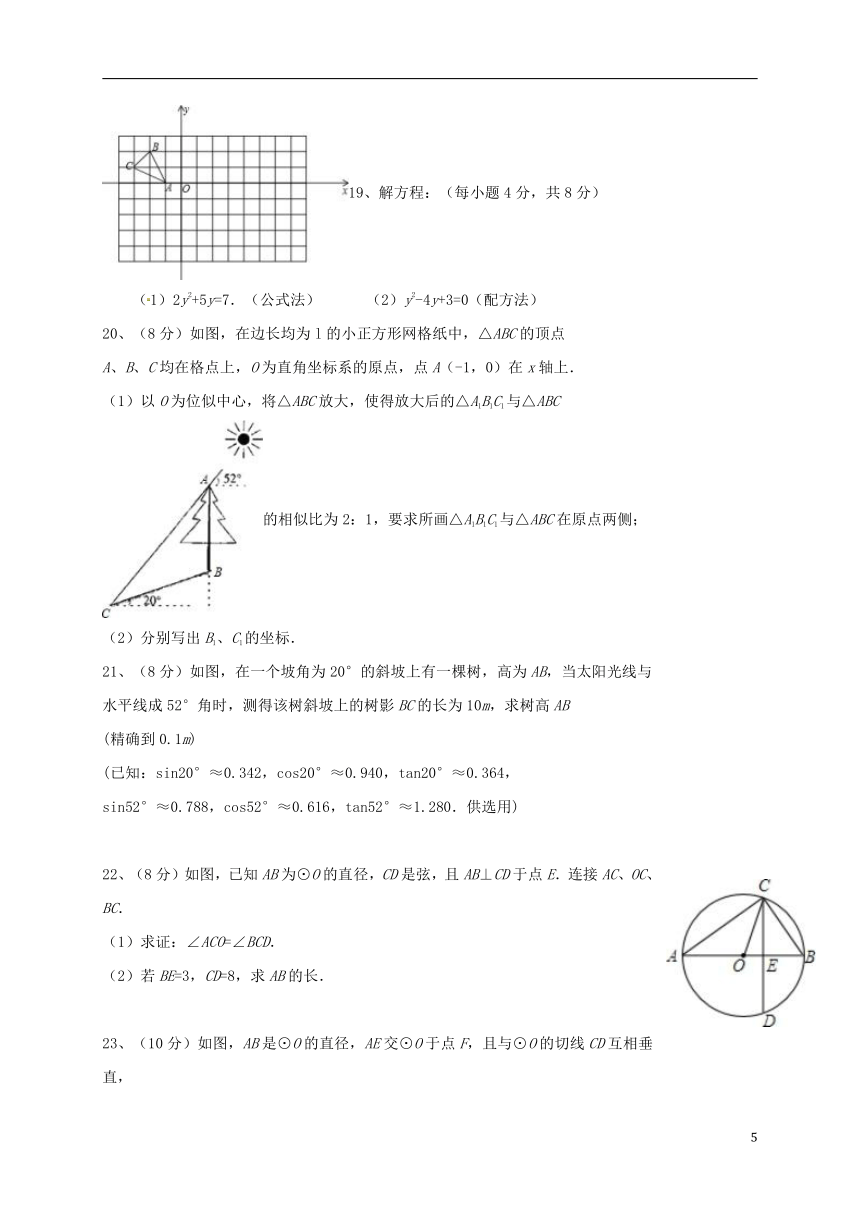
(1)2y2+5y=7.(公式法) (2)y2-4y+3=0(配方法) 20、(8分)如图,在边长均为l的小正方形网格纸中,△ABC的顶点
A、B、C均在格点上,O为直角坐标系的原点,点A(-1,0)在x轴上. (1)以O为位似中心,将△ABC放大,使得放大后的△A1B1C1与△ABC
的相似比为2:1,要求所画△A1B1C1与△ABC在原点两侧; (2)分别写出B1、C1的坐标. 21、(8分)如图,在一个坡角为20°的斜坡上有一棵树,高为AB,当太阳光线与
水平线成52°角时,测得该树斜坡上的树影BC的长为10m,求树高AB
(精确到0.1m) (已知:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364,
sin52°≈0.788,cos52°≈0.616,tan52°≈1.280.供选用) 22、(8分)如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC. (1)求证:∠ACO=∠BCD. (2)若BE=3,CD=8,求AB的长.
23、(10分)如图,AB是⊙O的直径,AE交⊙O于点F,且与⊙O的切线CD互相垂直,
垂足为D. (1)求证:∠EAC=∠CAB;(2)若CD=4,AD=8,求⊙O的半径;
24、(8分)如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据:≈1.41,结果精确到0.1米)
25、(11分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,
过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.
2017——2018学年度第一学期期中考试九年级数学试题
参考答案
1. D 2. B 3. D 4. C 5. C 6. B 7. C 8. D 9. D 10. C 11. B 12. B
13.
14. 8
15. 直径所对的圆周角为直角
16. 2
17. 【或】
18. 解:(1)原式=+-1=1-1=0; (2)原式=+2-2+1=.
19. 解:(1)原方程整理成一般式可得2y2+5y-7=0, ∵a=2,b=5,c=-7, ∴△=25-4×2×(-7)=81>0, 则y=, ∴y=1或y=-; (2)∵y2-4y=-3, ∴y2-4y+4=-3+4,即(y-2)2=1, 则y-2=1或y-2=-1,解得:y=3或y=1.
20解:(1)所画图形如下所示: △A1B1C1即为所求——————4分 (2)B1、C1的坐标分别为:(4,-4),(6,-2).——8分
21、.解:作CD⊥AB于D. 在Rt△BCD中,BC=10m,∠BCD=20°, ∴CD=BC?cos20°≈10×0.940=9.40(m),——2分 BD=BC?sin20°≈10×0.342=3.42(m);——4分 在Rt△ACD中,CD=9.40m,∠ACD=52°, ∴AD=CD?tan52°≈9.40×1.280=12.032(m).——6分 ∴AB=AD-BD=12.032-3.42≈8.6(m). 答:树高8.6米.——8分
22. 解:(1)∵AB为⊙O的直径, ∴∠ACB=90°, ∴∠A+∠B=90°, ∵AB⊥CD, ∴∠BCD+∠B=90°, ∴∠A=∠BCD, ∵OA=OC, ∴∠A=∠ACO, ∴∠ACO=∠BCD;————4分 (2)∵AB⊥CD, ∴CE=CD=4, ∴BC==5.
∵AB为⊙O的直径,AB⊥CD,
∴∠ACB=∠CEB=90°
∵∠B=∠B
∴△ACB∽△CEB
∴
∴AB= ————8分
23. (1)证明:连接OC. ∵CD是⊙O的切线, ∴CD⊥OC, 又∵CD⊥AE, ∴OC∥AE, ∴∠1=∠3, ∵OC=OA, ∴∠2=∠3, ∴∠1=∠2, 即∠EAC=∠CAB; ————5分 (2)解:①连接BC. ∵AB是⊙O的直径,CD⊥AE于点D, ∴∠ACB=∠ADC=90°, ∵∠1=∠2, ∴△ACD∽△ABC, ∴, ∵AC2=AD2+CD2=42+82=80, ∴AB==10, ∴⊙O的半径为10÷2=5.————10分
24. 解:作EF⊥AC, 根据题意,CE=18×15=270米,——1分 ∵tan∠CED=1, ∴∠CED=∠DCE=45°, ∵∠ECF=90°-45°-15°=30°,——3分 ∴EF=CE=135米,——4分 ∵∠CEF=60°,∠AEB=30°, ∴∠AEF=180°-45°-60°-30°=45°————5分, ∴AE=135≈190.4米,答:略。——————8分
25. 解:(1)相切,————1分
理由如下: 连接AD,OD, ∵AB为⊙O的直径, ∴∠ADB=90°. ∴AD⊥BC. ∵AB=AC, ∴CD=BD=BC. ∵OA=OB, ∴OD∥AC. ∴∠ODE=∠CED. ∵DE⊥AC, ∴∠ODE=∠CED=90°. ∴OD⊥DE. ∴DE与⊙O相切.————6分 (2)由(1)知∠ADC=90°, ∴在Rt△ADC中,由勾股定理 得 AD==4. ∵SACD=AD?CD=AC?DE, ∴×4×3=×5DE. ∴DE=.————11分
时间:120分钟;满分:120分
一、选择题(本大题共12小题,共36分)
1、下列方程中,是一元二次方程的是( )
A. 2x-y=3
B. x2+=2
C. x2+1=x2-1
D. x(x-1)=0
2、下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在
格点上,则在网格图中的三角形与△ABC相似的是( )
A.
B.
C.
D.
3、如图,AB是⊙O的直径,CD是弦,∠ABC=65°,则∠D的度数为( )
A. 130°
B. 65°
C. 35°
D. 25°
4、如图,在⊙O中,直径AB与弦CD垂直相交于点E,连结AC,OC,若∠A=30°,OC=4,则弦CD的长是( )
A.
B. 4
C.
D. 8
5、△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC
于D,下列选项中,错误的是( )
A. sinα=cosα
B. tanC=2
C. sinβ=cosβ
D. tanα=1
6、关于x的一元二次方程(m-1)x2+2x+m2-5m+4=0,常数项为0,则m值等于( )
A. 1
B. 4
C. 1或4
D. 0
7、如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
A. 6
B. 8
C. 10
D. 12
8、如图,在△ABC中,点P在边AB上,则在下列四个条件中::①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP?AB;④AB?CP=AP?CB,能满足△APC与△ACB相似的条件是( )
A. ①②④
B. ①③④
C. ②③④
D. ①②③
9、如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
A. 2000米
B. 4000米
C. 2000米
D. (2000+500)米
10、小明同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),则∠APB的度数为( )
A. 45°
B. 135°
C. 45°或135°
D. 90°或135°
11、如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
A. 4或4.8
B. 3或4.8
C. 2或4
D. 1或6
12、如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
A. 16
B. 24-4π
C. 32-4π
D. 32-8π
二、填空题(本大题共5小题,共15分)
13、已知CD是Rt△ABC斜边上的高线,且AB=10,若BC=8,则cos∠ACD= ______ .
14、如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高CD为 米.
15、阅读下面材料: 在数学课上,老师提出如下问题: 尺规作图:作Rt△ABC,使其斜边AB=c,一条直角边BC=a. 已知线段a,c如图. 小芸的作法如下: ① 取AB=c,作AB的垂直平分线交AB于点O; ② 以点O为圆心,OB长为半径画圆; ③ 以点B为圆心,a长为半径画弧,与⊙O交于点C;④ 连接BC,AC. 则Rt△ABC即为所求.老师说:“小芸的作法正确.” 请回答:小芸的作法中判断∠ACB是直角的依据是 .
16、已知一个正六边形的边心距为,则它的半径为______ .
17、如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,…,按此规律继续下去,则矩形ABnCnCn-1的面积为 .
三、解答题
18、计算:(每小题4分,共8分)
(1)sin260°+cos260°-tan45°; (2)|-|+-4cos45°+2sin30°. 19、解方程:(每小题4分,共8分)
(1)2y2+5y=7.(公式法) (2)y2-4y+3=0(配方法) 20、(8分)如图,在边长均为l的小正方形网格纸中,△ABC的顶点
A、B、C均在格点上,O为直角坐标系的原点,点A(-1,0)在x轴上. (1)以O为位似中心,将△ABC放大,使得放大后的△A1B1C1与△ABC
的相似比为2:1,要求所画△A1B1C1与△ABC在原点两侧; (2)分别写出B1、C1的坐标. 21、(8分)如图,在一个坡角为20°的斜坡上有一棵树,高为AB,当太阳光线与
水平线成52°角时,测得该树斜坡上的树影BC的长为10m,求树高AB
(精确到0.1m) (已知:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364,
sin52°≈0.788,cos52°≈0.616,tan52°≈1.280.供选用) 22、(8分)如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC. (1)求证:∠ACO=∠BCD. (2)若BE=3,CD=8,求AB的长.
23、(10分)如图,AB是⊙O的直径,AE交⊙O于点F,且与⊙O的切线CD互相垂直,
垂足为D. (1)求证:∠EAC=∠CAB;(2)若CD=4,AD=8,求⊙O的半径;
24、(8分)如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据:≈1.41,结果精确到0.1米)
25、(11分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,
过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.
2017——2018学年度第一学期期中考试九年级数学试题
参考答案
1. D 2. B 3. D 4. C 5. C 6. B 7. C 8. D 9. D 10. C 11. B 12. B
13.
14. 8
15. 直径所对的圆周角为直角
16. 2
17. 【或】
18. 解:(1)原式=+-1=1-1=0; (2)原式=+2-2+1=.
19. 解:(1)原方程整理成一般式可得2y2+5y-7=0, ∵a=2,b=5,c=-7, ∴△=25-4×2×(-7)=81>0, 则y=, ∴y=1或y=-; (2)∵y2-4y=-3, ∴y2-4y+4=-3+4,即(y-2)2=1, 则y-2=1或y-2=-1,解得:y=3或y=1.
20解:(1)所画图形如下所示: △A1B1C1即为所求——————4分 (2)B1、C1的坐标分别为:(4,-4),(6,-2).——8分
21、.解:作CD⊥AB于D. 在Rt△BCD中,BC=10m,∠BCD=20°, ∴CD=BC?cos20°≈10×0.940=9.40(m),——2分 BD=BC?sin20°≈10×0.342=3.42(m);——4分 在Rt△ACD中,CD=9.40m,∠ACD=52°, ∴AD=CD?tan52°≈9.40×1.280=12.032(m).——6分 ∴AB=AD-BD=12.032-3.42≈8.6(m). 答:树高8.6米.——8分
22. 解:(1)∵AB为⊙O的直径, ∴∠ACB=90°, ∴∠A+∠B=90°, ∵AB⊥CD, ∴∠BCD+∠B=90°, ∴∠A=∠BCD, ∵OA=OC, ∴∠A=∠ACO, ∴∠ACO=∠BCD;————4分 (2)∵AB⊥CD, ∴CE=CD=4, ∴BC==5.
∵AB为⊙O的直径,AB⊥CD,
∴∠ACB=∠CEB=90°
∵∠B=∠B
∴△ACB∽△CEB
∴
∴AB= ————8分
23. (1)证明:连接OC. ∵CD是⊙O的切线, ∴CD⊥OC, 又∵CD⊥AE, ∴OC∥AE, ∴∠1=∠3, ∵OC=OA, ∴∠2=∠3, ∴∠1=∠2, 即∠EAC=∠CAB; ————5分 (2)解:①连接BC. ∵AB是⊙O的直径,CD⊥AE于点D, ∴∠ACB=∠ADC=90°, ∵∠1=∠2, ∴△ACD∽△ABC, ∴, ∵AC2=AD2+CD2=42+82=80, ∴AB==10, ∴⊙O的半径为10÷2=5.————10分
24. 解:作EF⊥AC, 根据题意,CE=18×15=270米,——1分 ∵tan∠CED=1, ∴∠CED=∠DCE=45°, ∵∠ECF=90°-45°-15°=30°,——3分 ∴EF=CE=135米,——4分 ∵∠CEF=60°,∠AEB=30°, ∴∠AEF=180°-45°-60°-30°=45°————5分, ∴AE=135≈190.4米,答:略。——————8分
25. 解:(1)相切,————1分
理由如下: 连接AD,OD, ∵AB为⊙O的直径, ∴∠ADB=90°. ∴AD⊥BC. ∵AB=AC, ∴CD=BD=BC. ∵OA=OB, ∴OD∥AC. ∴∠ODE=∠CED. ∵DE⊥AC, ∴∠ODE=∠CED=90°. ∴OD⊥DE. ∴DE与⊙O相切.————6分 (2)由(1)知∠ADC=90°, ∴在Rt△ADC中,由勾股定理 得 AD==4. ∵SACD=AD?CD=AC?DE, ∴×4×3=×5DE. ∴DE=.————11分
同课章节目录
