6.3 特殊的平行四边形 复习课件

课件30张PPT。 第一章 特殊的平行四边形复习课学习目标:1、通过梳理特殊平行四边形的有关知识，构建网络，使知识系统化、结构化，加深对矩形、菱形、正方形知识的理解与记忆。
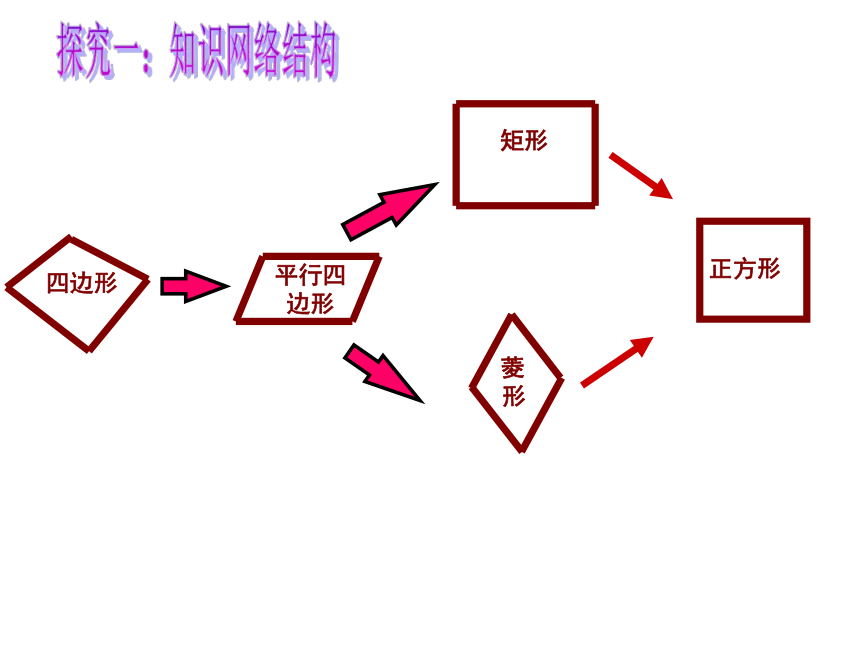
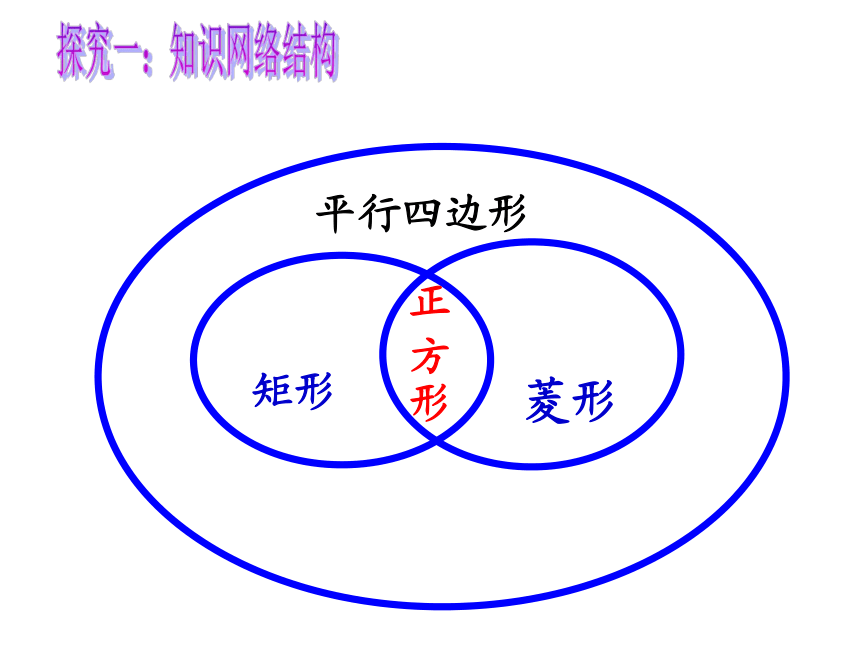
2、通过典型例题讲解，揭示解题规律，总结解题方法，进一步掌握特殊平行四边形的性质及判定方法，并能熟练应用性质及判定方法解决问题。探究一：知识网络结构正方形菱形矩形平行四边形探究一：知识网络结构知识点1：矩形的性质和判定定义：_________________________有一个内角是直角的平行四边形性质：边_____________
角__________________
对角线________________________判定：①_____________________是矩形
②_____________________是矩形
③_____________________是矩形对边平行且相等四个角都是直角互相平分且相等三个角是直角的四边形对角线相等的平行四边形有一个角是直角的平行四边形探究二：知识梳理知识点2：菱形性质与判定定义：_________________________一组邻边相等的平行四边形性质：边_____________
角__________________
对角线________________________判定：①_____________________是菱形
②_____________________是菱形
③_____________________是菱形四边相等对角相等，邻角互补互相垂直平分，且平分一组对角一组邻边相等的平行四边形对角线互相垂直的平行四边形四边都相等的四边形探究二：知识梳理知识点3：正方形的性质和判定定义：_________________________一组邻边相等的矩形叫做正方形 正方形具有平行四边形，矩形，菱形 的一切性质判定：①__________________是正方形
②__________________是正方形
③ __________________是正方形
④ __________________是正方形
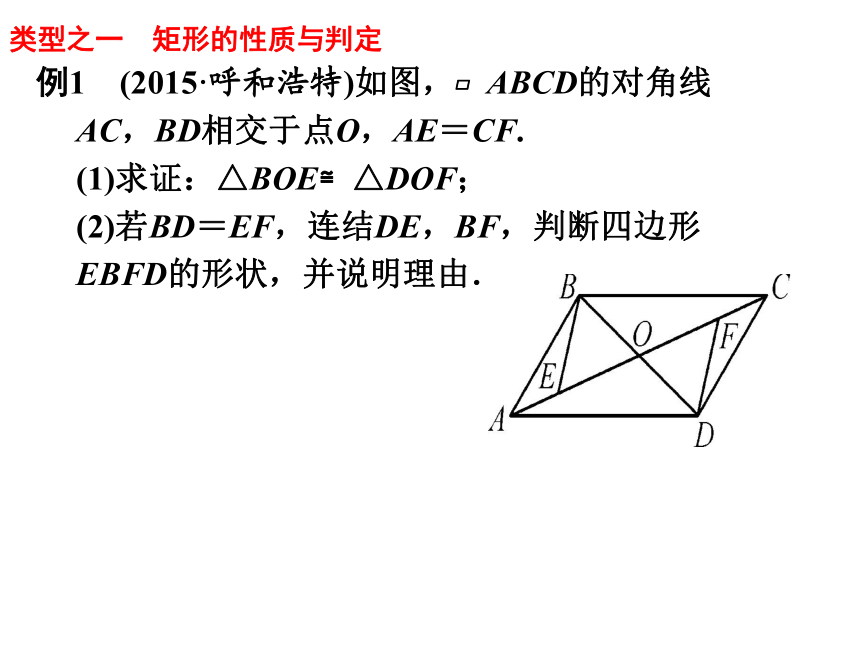
邻边相等的矩形有一个角是直角的菱形性质：探究二：知识梳理有一个角是直角的菱形对角线相等的菱形特殊平行四边形的性质探究三：总结归纳周长公式：面积公式：①有一个角是直角的平行四边形是矩形②对角线相等的平行四边形是矩形③有三个角是直角的四边形是矩形①有一组邻边相等的平行四边形是菱形　②四条边都相等的四边形是菱形　③对角线互相垂直的平行四边形是菱形　①一组邻边相等的矩形是正方形③有一个角是直角的菱形是正方形②对角线互相垂直的矩形是正方形④对角线相等的菱形是正方形特殊平行四边形的判定定理探究三：总结归纳 矩形是有一个角是直角的特殊平行四边形，它具有平行四边形的一切性质；判定矩形往往是先判定一个四边形是平行四边形，再结合一个直角或对角线相等来证明．探究四：性质和判定定理运用类型之一　矩形的性质与判定例1　(2015·呼和浩特)如图，?ABCD的对角线AC，BD相交于点O，AE＝CF.
(1)求证：△BOE≌△DOF；
(2)若BD＝EF，连结DE，BF，判断四边形EBFD的形状，并说明理由．类型之一　矩形的性质与判定【小结】从全等三角形的判定方法入手，以及矩形的判定定理寻找思路．如果题目中的矩形变为正方形(图2），结论又会变为什么？如果题目中的矩形变为菱形(图1），结论会变为什么？ 练习1：如图，矩形ABCD的对角线AC、BD交于点O，过点D作DP∥OC，且 DP=OC，连结CP，试判断四边形CODP的形状． 在证明一个四边形是菱形时，要注意判定条件是平行四边形不是任意四边形，任意四边形，则需证四条边都相等，若是平行四边形，则需利用对角线互相垂直或一组邻边相等来证明．菱形是特殊的平行四边形，除具有平行四边形的性质外，还有其特殊性质：四条边都相等，对角线互相垂直且每一条对角线平分一组对角．类型之二　菱形的性质与判定例2.如图，菱形ABCD中，∠ABC=60°,有一60°角的三角板绕点A旋转。
（1）若∠MAN的两边AM、AN分别交BC、CD于点E、F,则线段CE、DF的大小关系如何？请证明你的结论
（2）若∠MAN的两边AM、AN分别交BC、CD的延长线于点E、F,则线段CE、DF还有（1）中的结论吗？请说明你的理由。类型之二　菱形的性质与判定例2.在菱形ABCD中，∠ABC=60°,有一度数为60°的∠MAN绕点A旋转。
（1）若∠MAN的两边AM、AN分别交BC、CD于点E、F,则线段CE、DF的大小关系如何？请证明你的结论连接AC△AEC≌△AFD（ASA）例2.在菱形ABCD中，∠ABC=60°,有一度数为60°的∠MAN绕点A旋转。
（2）若∠MAN的两边AM、AN分别交BC、CD的延长线于点E、F,则线段CE、DF还有（1）中的结论吗？请说明你的理由。连接AC△AEC≌△AFD（ASA）【总结】1、熟练应用菱形的性质．
2、辅助线的作法练习2、已知如图，△ABC中AD平分∠BAC，DE∥AB交AC于F， DF∥AC交AB于E。四边形AFDE是怎样的四边形？说明你的理由。
正方形是特殊的平行四边形，还是特殊的矩形，特殊的菱形，因此正方形具有这些图形的所有性质；正方形的判定方法有两类：(1)先判定四边形是矩形，再判定这个矩形是正方形；(2)先判定四边形是菱形，再判定这个菱形是正方形．类型之三　正方形的性质与判定例3　已知：如图，正方形ABCD中M是AB的中点，E是AB的延长线上一点，MN⊥DM且交∠CBE的平分线于N(如图①)．类型之三　正方形的性质与判定(1)求证：MD＝MN；
(2)若将上述条件中“M是AB中点”改为“M是AB上任意一点”，其余条件不变(如图②)，则结论“MD＝MN”还成立吗？如果成立，请证明；如果不成立，请说明理由． (1)求证：MD＝MN；
(2)若将上述条件中“M是AB中点”改为“M是AB上任意一点”，其余条件不变(如图②)，则结论“MD＝MN”还成立吗？如果成立，请证明；如果不成立，请说明理由．
【解析】 (1)取AD的中点F，连结FM，则AF＝FD＝AM＝MB，∠AFM＝∠AMF＝45°，可得∠DFM＝∠MBN＝135°.由∠DMN＝90°，得到∠DMF＋∠NMB＝90°－45°＝45°.又∠FDM＋∠DMF＝45°，得∠FDM＝∠NMB，于是可证△DMF≌△MNB(ASA)，所以DM＝MN；
(2)同理可证MD＝MN.类型之三　正方形的性质与判定 ①　　　　　　　　　　②(2)结论MD＝MN还成立．
如图②，在AD上取一点F，使DF＝MB，连结MF，证法同(1)，证△DFM≌△MBN，即可得MD＝MN.【总结】1、用特殊图形的思想方法推出一般的方法．
2、辅助线的作法类型之四　特殊平行四边形的综合问题
例4.以△ABC的边AB、AC为边的等边三角形ABD和等边三角形ACE，四边形ADFE是平行四边形.
（1）当∠BAC等于 时，平行四边形ADFE不存在；
（2）当∠BAC等于 时，四边形ADFE是矩形；
（3）当△ABC分别满足什么条件时，平行四边形是菱形、正方形.解:（3) AB=AC时，平行四边形ADFE时菱形。
AB=AC且∠BAC=150°时，平行四边形ADFE是正方形。60°150°【总结】转化化归数学思想．课堂小结1、　如图，矩形ABCD的对角线AC，BD相交于点O，CE∥BD，DE∥AC，若AC＝4，则四边形CODE的周长是( ) A．4 B．6 C．8 D．102．如图，菱形ABCD中，AB=4，∠BAD＝60°，E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值是______. 达标检测1、　如图，矩形ABCD的对角线AC，BD相交于点O，CE∥BD，DE∥AC，若AC＝4，则四边形CODE的周长是( ) A．4 B．6 C．8 D．10C2．如图，菱形ABCD中，AB=4，∠BAD＝60°，E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值是______. 。4达标检测3、如图，已知四边形ABCD是边长为2的正方形，以对角线BD为边作正三角形BDE，过E作DA的延长线的垂线EF，垂足为F。
（1）找出图中与EF相等的线段，并证明你的结论；
（2）求AF的长。