简单机械例题[上学期]

有关杠杆应用的例题
　
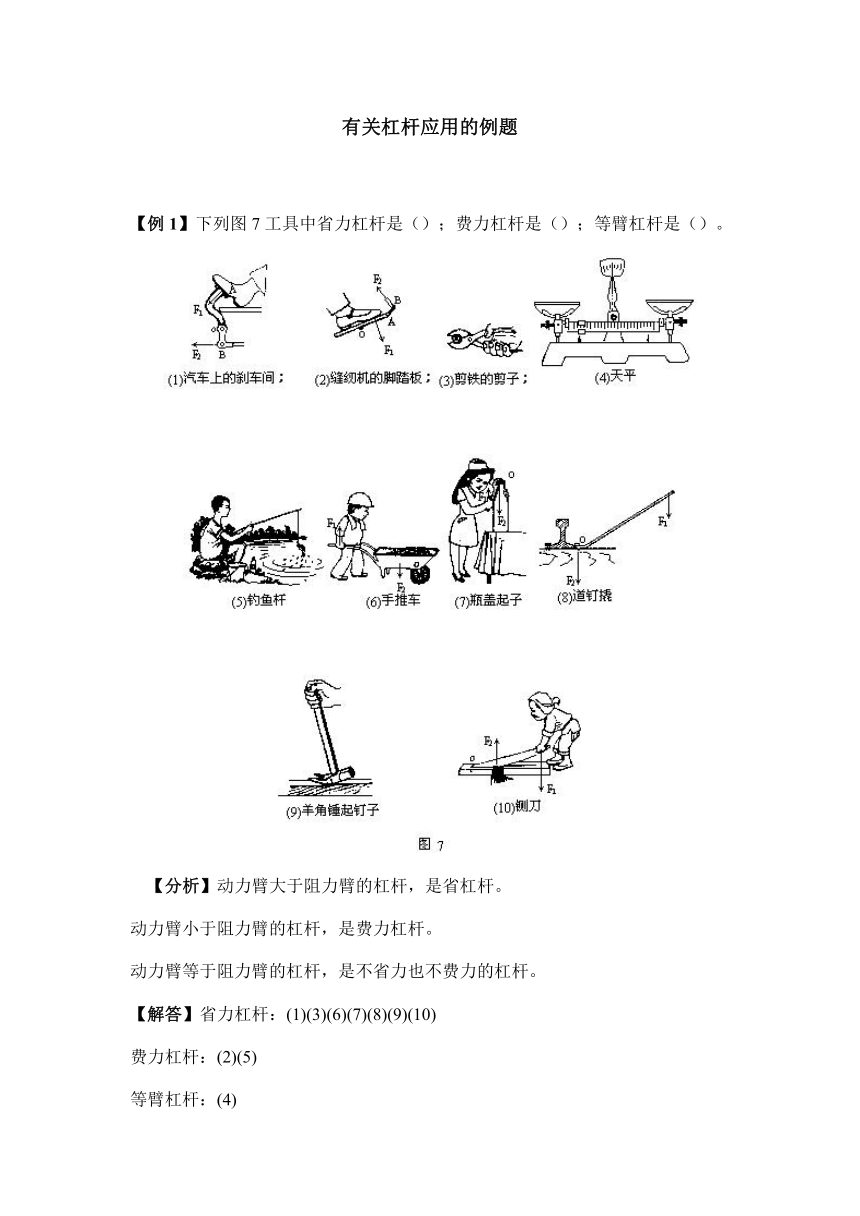
【例1】下列图7工具中省力杠杆是（）；费力杠杆是（）；等臂杠杆是（）。
　
　
　【分析】动力臂大于阻力臂的杠杆，是省杠杆。
动力臂小于阻力臂的杠杆，是费力杠杆。
动力臂等于阻力臂的杠杆，是不省力也不费力的杠杆。
【解答】省力杠杆：(1)(3)(6)(7)(8)(9)(10)
费力杠杆：(2)(5)
等臂杠杆：(4)
【说明】判断杠杆的种类常用两种方法。
一种是用
另一种是若阻力作用点在中间时，是省力杠杆。
若动力作用在中间时，是费力杠杆。
　
【例2】一把杆秤不计自重，提纽到秤钩距离是4cm，秤砣质量250g。用来称质量是2kg的物体，秤砣应离提纽多远，秤杆才平衡？若秤杆长60cm，则这把秤最大能称量多少千克的物体？
【分析】杆秤也是一个杠杆。若将秤砣重力看作动力，秤砣离提纽距离是动力臂；则被称物重力就是阻力，物体离提纽距离是阻力臂；提纽处即杠杆支点。
【解】由F1L1=F2L2，得
∴l'1=60cm 4cm=56cm.
由F'1l1=F'2l'2，得
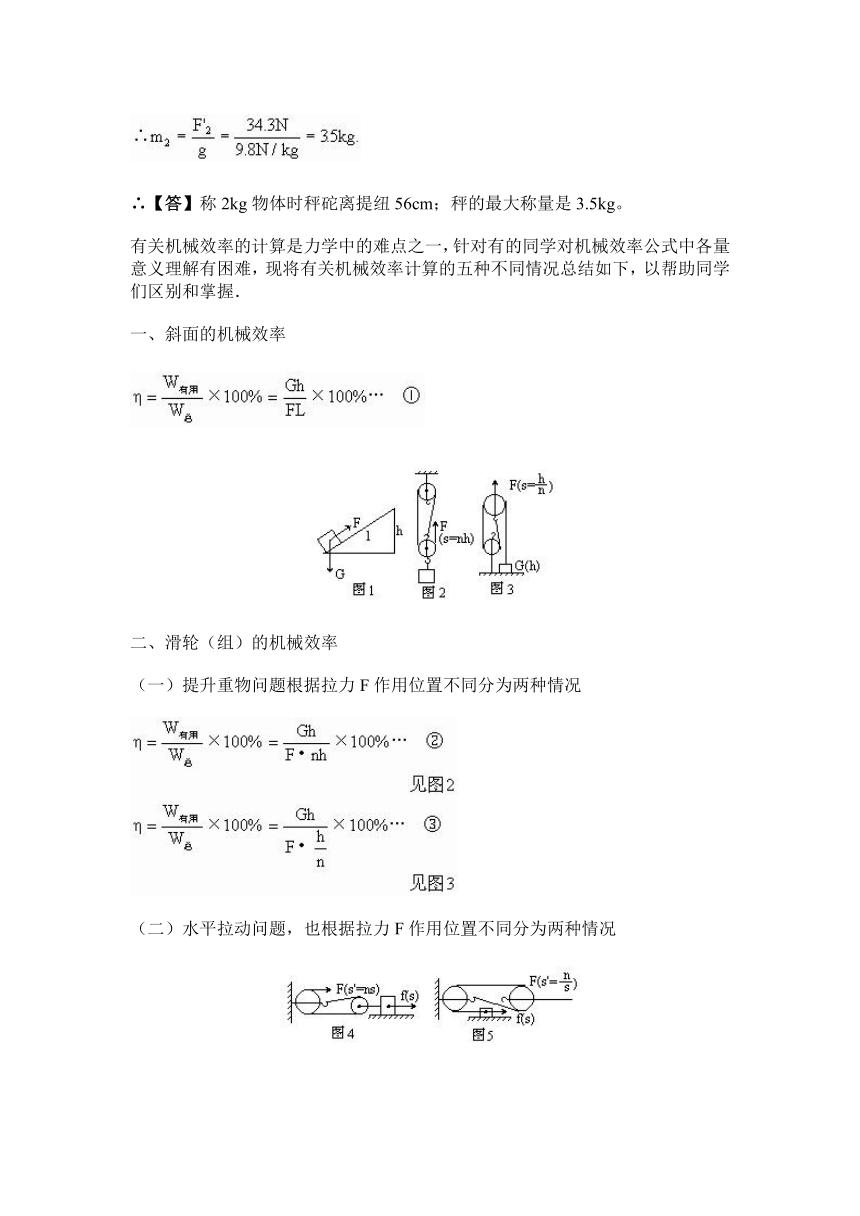
∴【答】称2kg物体时秤砣离提纽56cm；秤的最大称量是3.5kg。
有关机械效率的计算是力学中的难点之一，针对有的同学对机械效率公式中各量意义理解有困难，现将有关机械效率计算的五种不同情况总结如下，以帮助同学们区别和掌握．
一、斜面的机械效率
二、滑轮（组）的机械效率
（一）提升重物问题根据拉力F作用位置不同分为两种情况
（二）水平拉动问题，也根据拉力F作用位置不同分为两种情况
　
例1重为200N的物体沿长5m高2m的斜面在平行于斜面的拉力F作用下匀速运动到顶端，已知斜面的机械效率为80％，求①拉力F的大小．②物体受到摩擦力的大小．
分析；这是一个有关斜面机械效率计算的典型例子．拉力F可由公式①直接计算得出．关键是物体受到的摩擦力的计算．我们知道利用斜面时，由于摩擦的存在而必须做额外功，如果斜面对物体的摩擦不存在，那么额外功就为零，根据功的原理就有F＇l=Gh，可得F＇，那么两者之差F—F’即为物体在斜面所受的摩擦力f．
（2）如果斜面没有摩擦，则有F＇l=Gh
∴f=F－F＇=100N－80N=20N
例2．用图三装置提拉物体，已知 F=g00N，装置的机械效率η=75％，若不计滑轮重，问可提起多重的物体．
分析：解有关滑轮（组）的机械效率问题时，首先要分清滑轮是用来提升物体还是水平拉物体，前者用公式②、③，后者用公式④⑤；然后再注意拉力F的作用位置，是作用在连接滑轮间的绳子上，还是作用在滑轮的轴上，前者用公式②、④后者用公式③⑤．经过分析本题是提升物体，F作用在滑轮的轴上，故用公式③
例3重为400N的物体，用如右图所示的滑轮组在F=25N作用下，物体以0．8m／s的速度匀速前进，已知滑轮组的机械效率为80%，求（l）物体受到的摩擦力．（2）F的功率。
　
分析：根据上题的分析思路，可知应用公式④．在公式中还有一个较易搞错的量——n，（即连接在动滑轮上的绳子股数）这题中n应取4．第2小题F的功率在已知F的情况下，常可用P=F·v应特别注意的是题中的0.8m／S不是拉力F移动速度．事实上根据拉力移动距离和物体移动距离的关系，可得vF=4v物．
得f＝F·4η·s/s=25N×4×80％=80N
2）由题意可知vF=4×v物=4×0.8m/S=3.2m/s
则P=F·vF=25N×3.2m/s=80W
关于滑轮组机械效率的错误例析
山东 于正和
　　"机械效率"是初中物理的重要概念之一，也是学生学习的难点，尤其是关于滑轮组的机械效率．学生在处理这类问题时，常常出现这样那样的错误．下面归类总结，以利于学生学习．
　　错误一：使用动滑轮省力费距离
例1．如图1所示，物体A重200N，在水平拉力作用下以0.2m/s的速度匀速前进１分钟．若物体A在前进过程中受到的摩擦阻力为50N，滑轮组的机械效率为80%，求拉力F的大小及其功率．
　　错误解析：如图1所示，SA＝vAt＝0.2m/s×60s＝12m，
　　　　　　　　　　　　 W有＝fSA＝50N×12m＝600J，
　　　　　　　　　　　　 W总＝W总/η＝600J／80%＝750J，
　　　　　　　　　　　　 F＝W总/2SA＝750J／24m＝31.3N，
　　　　　　　　　　　　 P＝W总/t＝750J／60s＝12.5W．
　　该解错误的原因是没有看清题中的动力Ｆ作用在轴上，而不是作用在轮上．此题中的装置费力省距离，即动力移动的距离S是阻力移动的距离SA的一半，S＝SA/2．
　　正确解法：SA＝ vAt ＝ 0.2m/s×60s ＝ 12m，
　　　　　　　W有＝ fSA ＝ 50N×12m ＝ 600J，
　　　　　　　W总＝ W总/η ＝ 600J／80% ＝ 750J，
　　　　　　　S＝ SA/2 ＝ 6m，
　　　　　　　F＝ W总/S ＝ 125N．
　　　　　　　P＝ W总/t ＝ 750J／60s ＝ 12.5ｗ．
　　　　　　　　　　　　
　　错误二：同一滑轮组的机械效率保持不变
例2．现用图2所示的滑轮组提升重物．（不计摩擦和绳重）
　　（1）用250N的力将重为400N的物体匀速提升时,此滑轮组的机械效率是多少
　　（2）若用此滑轮组将重为900N的物体匀速提升2m,那么拉力做的功是多少
　　错误解析：如图2所示，η＝ W有/W总 × 100% ＝ Gh/Fh ＝ (400N/2×250N) × 100%＝80%．
　　　　　　　　　　　　　W'有 ＝ G/h = 900N×2m ＝1800J
　　　　　　　　　　　　　W'总 ＝W'有／η＝ 1800J／80% ＝2250 J.
　　此解犯了定势思维的错误，认为不同滑轮组的机械效率不同，则同一滑轮组的机械效率一定相同．事实上，增加同一滑轮组提升的重物的重力时，将增大有用功在总功中所占比例，即增大机械效率．
　　正确解法：（１）η＝ W有/W总 × 100% ＝ Gh/Fh ＝ (400N/2×250N) × 100%＝80%．
　　　　　　　（２）动滑轮的重力 G动 ＝ nF－G ＝ 2×250N－400N ＝ 100N，
　　　　　　　　　　η'＝ W有/W总 × 100% ＝ G'/(G'+G动) ＝ 900N/(900+100)N ＝90%，
　　　　　　　　　　W'有＝ G/h = 900N×2m ＝ 1800J
　　　　　　　　　　W'总＝ W'有／η ＝1800J/90% ＝2000J．
　　错误三：不能正确理解有用功和额外功
例3．如图3所示，用滑轮组将重为300N的物体A沿水平方向匀速拉动，物体A与水平面间的摩擦阻力为100N，若此滑轮组的机械效率为75%，物体A在水平拉力作用下１分钟内匀速前进50cm，求拉力的大小及其功率．
　　错误解析：W额＝ fSA ＝ 100N×0.5m ＝ 50 J，
　　　　　　　W总＝ W额/(1-η)＝ 50J/(1-75%) ＝200Ｊ，
　　　　　　　S＝ 3SA ＝ 6 m ＝ 3×0.5m ＝ 1.5m，
　　　　　　　F＝ W总/S ＝200Ｊ／1.5m＝133.3N，
　　　　　　　P＝ W总/t ＝200Ｊ／60s＝3.3ｗ．
　　该解的错误原因在于没有理解有用功和额外功的真正涵义．该题中利用滑轮组装置的目地是水平移动物体A，克服的有用阻力恰为物体A与水平面间的摩擦阻力，此时克服物体A与水平面间的摩擦阻力而做的功有用功；而克服滑动轮和轴之间的摩擦所做的功是额外功．
　　正确解法：W有 ＝ fSA ＝ 100N×0.5m ＝ 50 J，
　　　　　　　W总 ＝ W有/η ＝ 50J/75% ＝66.7Ｊ，
　　　　　　　S＝ 3SA ＝ 6 m ＝ 3×0.5m ＝ 1.5m，
　　　　　　　F＝ W总/S ＝ 66.7Ｊ／1.5m ＝ 44.4N，
　　　　　　　P＝ W总/t ＝ 66.7Ｊ／60s ＝1.1ｗ．
　　　　　　　　　　　　　　　　
　　错误四：公式F＝ (G＋ G轮)/n 中的G轮错误的认为是所有滑轮装置的总重量
例4．如图4所示，滑轮组的动滑轮装置和定滑轮装置的重量都是70N．（不计摩擦和绳重）
　　（1）若拉力F＝70N，重物在拉力Ｆ作用下匀速上升，求此滑轮组的机械效率．
　　（2）重物在4s内上升了2m，拉力做了多少功，功率是多大？
　　错误解析：（1）因F＝ (G＋ G轮)/n ，所以 G ＝ nF－G轮 ＝ 5×70N－2×70N＝ 210N，
　　　　　　　　　 η＝ W有/W总 × 100% ＝ G/nF×100% ＝ 60%．
　　　　　　　（2）W有＝ Gh = 210N×2m ＝ 420J，
　　　　　　　　　 W总＝ W有／η ＝ 420J/60% ＝ 700Ｊ，
　　　　　　　　　 P＝ W总/t ＝ 420Ｊ／4s ＝ 175W．
　　试验表明，使用滑轮组提升重物时，若不计摩擦，动滑轮被几股绳子吊起，所用的拉力就是物体和动滑轮总重的几分之一．所以，公式F＝(G＋ G轮)/n 中的G轮实际是指动滑轮装置总重，而不包括定滑轮装置总重．因此，将公式改写成F＝(G＋ G轮)/n ，学生容易理解．
　　正确解法：（1）因F＝(G＋ G轮)/n ，所以 G ＝ nF－G轮 ＝ 5×70N－70N ＝ 280N，
　　　　　　　　　 η＝ W有/W总 ×100%＝ G/nF×100% ＝ 280N/(5×70N) ＝ 80%．
　　　　　　　（2）W有 ＝ Gh= 280N×2m ＝ 560J，
　　　　　　　　　 W总＝ W有／η ＝ 420J/60% ＝ 700Ｊ，
　　　　　　　　　 P＝ W总/t ＝ 420Ｊ／4s ＝ 175W．
　　只要在学习中善于总结和积累经验，吸取教训，克服思维定势带来的负迁移，认真寻找问题的根源，逐步训练，就一定能把机械效率学好．