数学六年级上沪教版1.5能被2_5整除的数课件(21张)
文档属性
| 名称 | 数学六年级上沪教版1.5能被2_5整除的数课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 86.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-16 15:19:14 | ||
图片预览







文档简介
(共21张PPT)
1.5 能被2、5整除的数
1. 因数和倍数的意义.
复习引入
整数a能被整数b整除,a就叫做b的倍数,b就叫做a的因数(或约数).
2.生活中我们接触到的许多事物都是成对出现的,如一双鞋子、一双筷子….
如果小明的家中有3人用餐,那么要拿出 根筷子;
如果小明家来了客人,那么拿出的筷子的根数一定是 的倍数,即这个数是能被 整除的数.
复习引入
6
2
2
探究新知
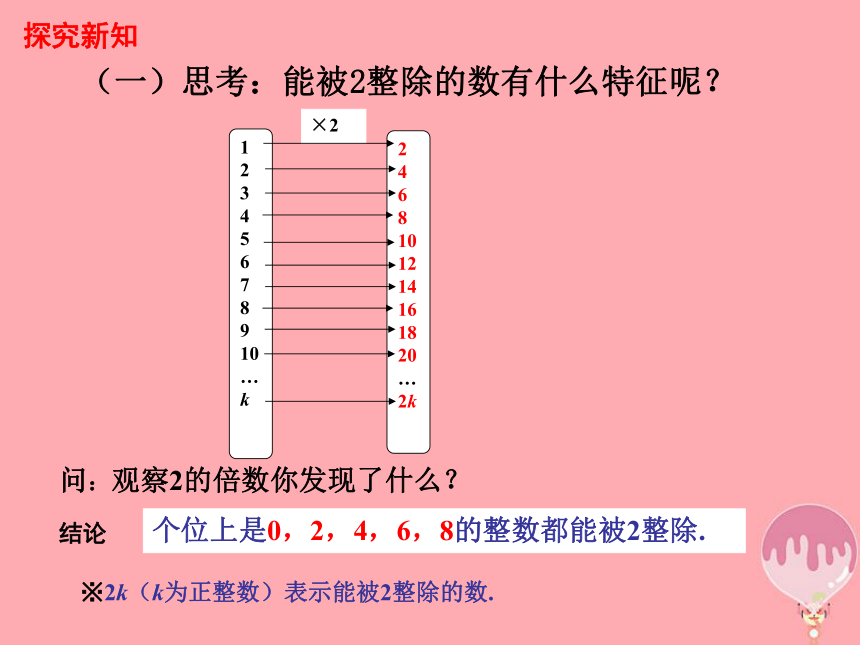
(一)思考:能被2整除的数有什么特征呢?
1
2
3
4
5
6
7
8
9
10
…
k
×2
2
4
6
8
10
12
14
16
18
20
…
2k
问:观察2的倍数你发现了什么?
个位上是0,2,4,6,8的整数都能被2整除.
结论
※2k(k为正整数)表示能被2整除的数.
探究新知
(二)奇数和偶数的意义
1. 翻开你的数学课本,所有左边的页码都能被2整除吗?所有右边的页码都能被2整除吗?左边和右边页码个位上的数各有什么特征?
2. 偶数:能被2整除的整数叫做偶数,
奇数:不能被2整除的整数叫做奇数.
3. 正整数按照能否被2整除分类:
正整数
4.问题:
(1)奇数的个位上的数有什么特点呢?
奇数的个位上的数是奇数.
(2)在连续的正整数中(除了1外),与奇数相邻的两个数是奇数还是偶数?与偶数相邻的两个数呢?
与奇数相邻的两个数是偶数,
与偶数相邻的两个数是奇数.
※ 与偶数2k相邻的两个数是奇数 和 .
探究新知
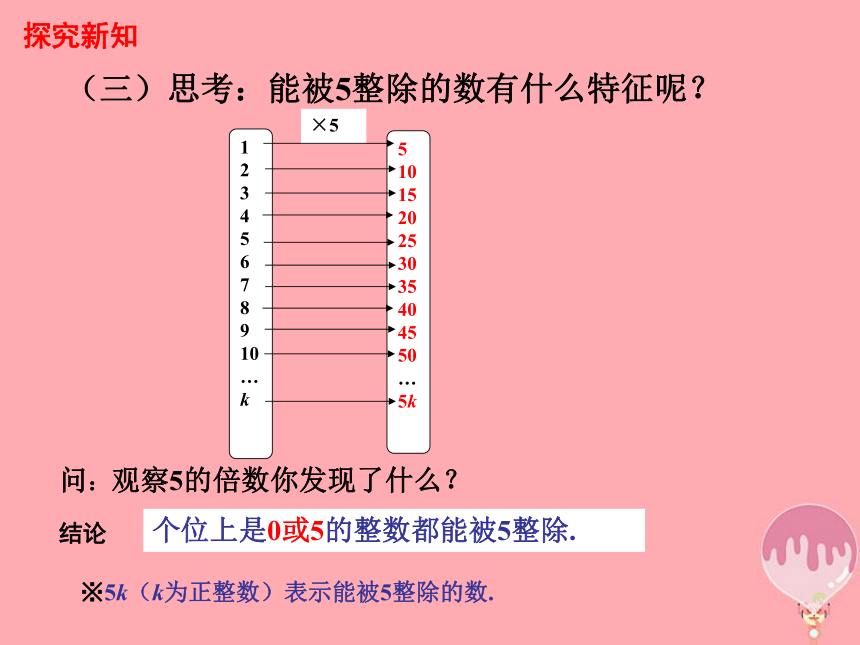
(三)思考:能被5整除的数有什么特征呢?
1
2
3
4
5
6
7
8
9
10
…
k
×5
5
10
15
20
25
30
35
40
45
50
…
5k
问:观察5的倍数你发现了什么?
个位上是0或5的整数都能被5整除.
结论
※5k(k为正整数)表示能被5整除的数.
运用新知
1. 下列数中,哪些数是奇数?哪些数是偶数?
19,32,87,10,11,153,66,445
奇数:19,87,11,153,445.
偶数:32,10,66.
运用新知
2. 在下列数中,
18,27,30,44,60,102,417,375,
(1)找出能被2整除的数;
(2)找出能被5整除的数;
能被2整除的数:18,30,44,60,102.
能被5整除的数:30,60,375.
(3) 哪些数既能被2整除又能被5整除?
思考:能同时被2和5整除的数有什么特征呢?
能同时被2和5整除的数:30,60.
个位上是0的整数都能同时被2和5整除.
结论
运用新知
3. 在1到20的自然数中,能被2整除的数有 个,能被5整除的数有 个.
10
4
想一想:在1到2010的自然数中,能被2整除的数有多少个?能被5整除的数又有多少个?
1005个,402个
4. 523至少加上 才能被2整除,至少加上 才能被5整除.
1
2
小结:在1到n的自然数中,当n为偶数时,能被2整除的数
有 个;当n为奇数时,能被2整除的数有 个.
运用新知
用5,6,8三个数字组成一个三位数,
(1)使它是2的倍数,那么这个三位数是多少?
(2)如果要使它是5的倍数,那么这个三位数又是多少呢?
685或865.
分析
要使这个三位数是2的倍数,它的个位上可以是6或8,
另两个数分别可以是十位上或百位上的数,所以有四种情况.
586或856或568或658.
分析
要使这个三位数是5的倍数,它的个位上是5,
6和8分别可以是十位上或百位上的数,所以有两种情况.
运用新知
6.选择题
三个连续偶数不可以表示为( )
A.2n-2,2n,2n+2
B.a-1,a,a+1
C.m,m+2,m+4
D.2(k+1),2k,2(k-1)
B
运用新知
7.在下列数中找出既能被2整除又能被5整除的数,填写在适当的圈内。这样的数有什么特点?
12,25,40,75,80,94,105,210
12,
94,
40,80,210
25,75,
105
课堂小结
通过这节课的学习,你有哪些收获与体会?
1.奇数和偶数的意义.
2.正整数按照能否被2整除分类:
正整数
3.能被2、5整除的数的特征.
回家作业
A组
1.下列哪些数有因数2?哪些数有因数5?
12,27,25,30,51,60,
75,96,186,225.
有因数2的数_____________________;
有因数5的数_____________________.
12,30,60,96,186 .
25,30,60,75,225
2.判断下列说法对吗?对的在括号内打“√”,错的打“×”.
(1)能被2整除的数一定是偶数. ( )
(2)两个相邻的奇数相差2. ( )
√
√
B组:
1.(1)写出两个能被5整除的偶数:_____________.
(2)写出两个能被5整除的奇数:______________.
(3)写出两个既能被5整除又能被2整除的数:_________.
10,60
15,35
10,20
2.在下列每个数的( )内填上一个数字,使得这个数有因数5.你还能写出几个?
5( ) ( )1( )
3.用3,0,5排成的三位数中,写出能被5整除的数.
5(0 )或5(5)
(1 )1(0 ),共能写出18个.
前一个( )里可以填1,2,3,4,5,6,7,8,9
,后一个( )里可以填0,5.
3.用3,0,5排成的三位数中,写出能被5整除的数.
305,350,530
C组:
1、“转糖盘”是一个固定不动的圆盘,盘面被平分为10格(如图)。在偶数格内放一块糖,在奇数格内放上值钱的物品。某人给摊主5角钱,即可沿着顺时针方向转动圆盘一次。圆盘停转后,指针指到哪一格,摊主便依据该格的数顺着圆盘转动方向从下一格起数格,数到哪一格,该格中的物品就归这个人。例如:指针停在3,则从4起再数3格,即第6格中的物品就是奖品.
实际上,不管您怎么转,永远都拿不到奇数格中的物品。请你试着填写下列表格,看看你的奖品是什么.
指针所
在格数 1 2 3 4 5 6
奖品所
在格数
7 8 9 10
奖品都是一块糖
2、三个连续偶数之和是42,则他们中最小的偶数是几?最大的偶数是几?
1.5 能被2、5整除的数
1. 因数和倍数的意义.
复习引入
整数a能被整数b整除,a就叫做b的倍数,b就叫做a的因数(或约数).
2.生活中我们接触到的许多事物都是成对出现的,如一双鞋子、一双筷子….
如果小明的家中有3人用餐,那么要拿出 根筷子;
如果小明家来了客人,那么拿出的筷子的根数一定是 的倍数,即这个数是能被 整除的数.
复习引入
6
2
2
探究新知
(一)思考:能被2整除的数有什么特征呢?
1
2
3
4
5
6
7
8
9
10
…
k
×2
2
4
6
8
10
12
14
16
18
20
…
2k
问:观察2的倍数你发现了什么?
个位上是0,2,4,6,8的整数都能被2整除.
结论
※2k(k为正整数)表示能被2整除的数.
探究新知
(二)奇数和偶数的意义
1. 翻开你的数学课本,所有左边的页码都能被2整除吗?所有右边的页码都能被2整除吗?左边和右边页码个位上的数各有什么特征?
2. 偶数:能被2整除的整数叫做偶数,
奇数:不能被2整除的整数叫做奇数.
3. 正整数按照能否被2整除分类:
正整数
4.问题:
(1)奇数的个位上的数有什么特点呢?
奇数的个位上的数是奇数.
(2)在连续的正整数中(除了1外),与奇数相邻的两个数是奇数还是偶数?与偶数相邻的两个数呢?
与奇数相邻的两个数是偶数,
与偶数相邻的两个数是奇数.
※ 与偶数2k相邻的两个数是奇数 和 .
探究新知
(三)思考:能被5整除的数有什么特征呢?
1
2
3
4
5
6
7
8
9
10
…
k
×5
5
10
15
20
25
30
35
40
45
50
…
5k
问:观察5的倍数你发现了什么?
个位上是0或5的整数都能被5整除.
结论
※5k(k为正整数)表示能被5整除的数.
运用新知
1. 下列数中,哪些数是奇数?哪些数是偶数?
19,32,87,10,11,153,66,445
奇数:19,87,11,153,445.
偶数:32,10,66.
运用新知
2. 在下列数中,
18,27,30,44,60,102,417,375,
(1)找出能被2整除的数;
(2)找出能被5整除的数;
能被2整除的数:18,30,44,60,102.
能被5整除的数:30,60,375.
(3) 哪些数既能被2整除又能被5整除?
思考:能同时被2和5整除的数有什么特征呢?
能同时被2和5整除的数:30,60.
个位上是0的整数都能同时被2和5整除.
结论
运用新知
3. 在1到20的自然数中,能被2整除的数有 个,能被5整除的数有 个.
10
4
想一想:在1到2010的自然数中,能被2整除的数有多少个?能被5整除的数又有多少个?
1005个,402个
4. 523至少加上 才能被2整除,至少加上 才能被5整除.
1
2
小结:在1到n的自然数中,当n为偶数时,能被2整除的数
有 个;当n为奇数时,能被2整除的数有 个.
运用新知
用5,6,8三个数字组成一个三位数,
(1)使它是2的倍数,那么这个三位数是多少?
(2)如果要使它是5的倍数,那么这个三位数又是多少呢?
685或865.
分析
要使这个三位数是2的倍数,它的个位上可以是6或8,
另两个数分别可以是十位上或百位上的数,所以有四种情况.
586或856或568或658.
分析
要使这个三位数是5的倍数,它的个位上是5,
6和8分别可以是十位上或百位上的数,所以有两种情况.
运用新知
6.选择题
三个连续偶数不可以表示为( )
A.2n-2,2n,2n+2
B.a-1,a,a+1
C.m,m+2,m+4
D.2(k+1),2k,2(k-1)
B
运用新知
7.在下列数中找出既能被2整除又能被5整除的数,填写在适当的圈内。这样的数有什么特点?
12,25,40,75,80,94,105,210
12,
94,
40,80,210
25,75,
105
课堂小结
通过这节课的学习,你有哪些收获与体会?
1.奇数和偶数的意义.
2.正整数按照能否被2整除分类:
正整数
3.能被2、5整除的数的特征.
回家作业
A组
1.下列哪些数有因数2?哪些数有因数5?
12,27,25,30,51,60,
75,96,186,225.
有因数2的数_____________________;
有因数5的数_____________________.
12,30,60,96,186 .
25,30,60,75,225
2.判断下列说法对吗?对的在括号内打“√”,错的打“×”.
(1)能被2整除的数一定是偶数. ( )
(2)两个相邻的奇数相差2. ( )
√
√
B组:
1.(1)写出两个能被5整除的偶数:_____________.
(2)写出两个能被5整除的奇数:______________.
(3)写出两个既能被5整除又能被2整除的数:_________.
10,60
15,35
10,20
2.在下列每个数的( )内填上一个数字,使得这个数有因数5.你还能写出几个?
5( ) ( )1( )
3.用3,0,5排成的三位数中,写出能被5整除的数.
5(0 )或5(5)
(1 )1(0 ),共能写出18个.
前一个( )里可以填1,2,3,4,5,6,7,8,9
,后一个( )里可以填0,5.
3.用3,0,5排成的三位数中,写出能被5整除的数.
305,350,530
C组:
1、“转糖盘”是一个固定不动的圆盘,盘面被平分为10格(如图)。在偶数格内放一块糖,在奇数格内放上值钱的物品。某人给摊主5角钱,即可沿着顺时针方向转动圆盘一次。圆盘停转后,指针指到哪一格,摊主便依据该格的数顺着圆盘转动方向从下一格起数格,数到哪一格,该格中的物品就归这个人。例如:指针停在3,则从4起再数3格,即第6格中的物品就是奖品.
实际上,不管您怎么转,永远都拿不到奇数格中的物品。请你试着填写下列表格,看看你的奖品是什么.
指针所
在格数 1 2 3 4 5 6
奖品所
在格数
7 8 9 10
奖品都是一块糖
2、三个连续偶数之和是42,则他们中最小的偶数是几?最大的偶数是几?
