特殊元素法在数学解题中的应用教案

特殊元素法在数学解题中的应用
在解答数学问题时，我们经常要求学生注意问题的一般性，谨防出现特殊代替一般的错误.但在实际解题中，有时巧妙地应用满足题设条件的特殊元素，也能收到事半功倍之效.现举例说明，以供参考.
一、字母取值特殊化
例1
若，则的值为
.
分析
一般情况下能成立的结论，在特殊情况下也一定成立.由题意可知、、为非零实数，且其和为0，于是可对、、为赋以特殊值来求解.一般情况下所赋的特殊值应是较简单、便于计算的数值.
由，不妨设
原式
例2
因式分解后的结论是(
)
(A)
(B)
(C)
(D)
分析因为因式分解是恒等变形，不论、、取何实数，正确答案总是成立的，故可在原式中取特殊值求解.
不妨令，则原式.
而选项中只有(A)符合要求，故选(A).
二、字母关系特殊化
例3
方程，当每取一对数值就有一个关于的方程，而所有这些方程有一个公共解(即指一对确定的，它们满足所有这些方程)，试求出这个公共解.
分析
由于题设“当每取一对数值就有一个关于的方程”中，对的取值没有做出具体的限定，故结合方程中字母系数的特点，可利用特殊化方式求解.
于是，我们令
代入方程解得
令，代人方程解得
所以，即为所求的公共解.
三、图形位置关系的特殊化
例4
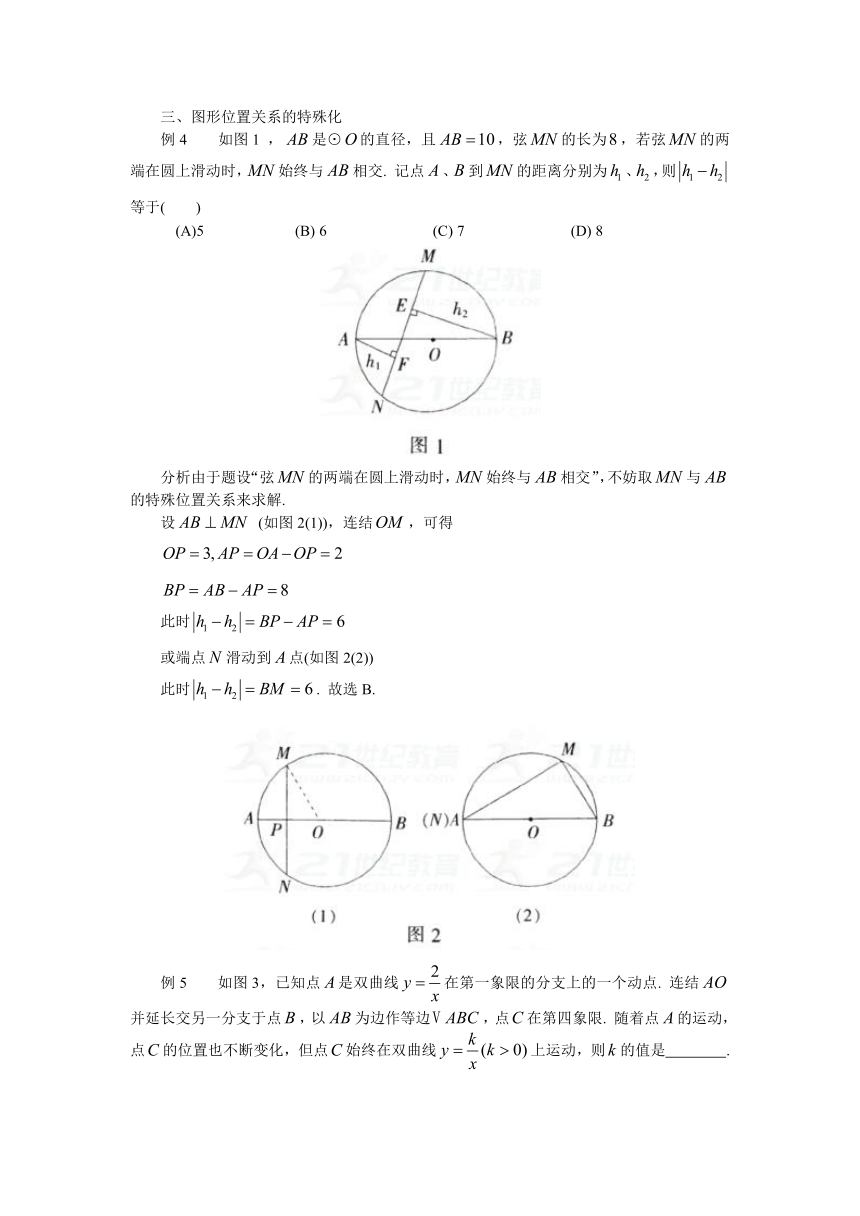
如图1
，是⊙的直径，且，弦的长为，若弦的两端在圆上滑动时，始终与相交.
记点、到的距离分别为、，则等于(
)
(A)5
(B)
6
(C)
7
(D)
8
分析由于题设“弦的两端在圆上滑动时，始终与相交”，不妨取与的特殊位置关系来求解.
设
(如图2(1))，连结，可得
此时
或端点滑动到点(如图2(2))
此时.
故选B.
例5
如图3，已知点是双曲线在第一象限的分支上的一个动点.
连结并延长交另一分支于点，以为边作等边，点在第四象限.
随着点的运动，点的位置也不断变化，但点始终在双曲线上运动，则的值是
.
分析
如图3，将的边取特殊位置，即轴，交轴于点，则的为等边三角形.
过点作轴于点
设点，可知，
∴点
∴
∴点
∴
四、角的度数特殊化
例6
如图5，在中，，，是高，点为的中点，则的长为
.
分析
由题设知，为任意三角形，且
可设特殊情形，则
∴为直角三角形，
而是高
∴
∴
又为的中点
∴
∴
五、图形形状特殊化
例7
如图6，一任意凸四边形，两组对边中点与的连线交于点，则图中与的面积之和占四边形面积的
.
分析
四边形既然是任意凸四边形，因此我们将其特殊化为正方形(如图7)，由正方形的相关性质，可得
例8
如图8，
.
分析
将图8特殊化为正五角星形，如图9.
则
故