一个基本模型在不同视角下前应用教案
图片预览

文档简介
一个基本模型在不同视角下前应用
【基本模型】
如图1,线段是中线,则有
分析
过点作,垂足为,根据等底等高,有
∵
∴
三角形的中线由等底等高把分成两个面积相等的三角形.利用这模型,可以解决许多有关多边形面积的问题.
一、借助几何模型进行图形的分割
问题1
园艺工人要将一块三角形花坛分成三个面积相等的小三角形,分别种植三种不同的花卉,应该如何分配该花坛
思路分析
可以把三角形先三等分,再把其中一个再两等分,所以联想到作三角形的中线.具体方法:利用中线等分三角形面积中等底等高的思想方法,先将三角形一边进行三等分,连结对面顶点及其中一个三等分点,将三角形面积分成1:2,再将两份的进行二等分.
在划分方法中有一个图形不同于其它图形,单独来研究一下具体做法:
如图2,作三边上的中线交于点,则、、为分割线
证明
∵是中边的中线
∴
同理,
∴
∴
同理,
∴
问题2
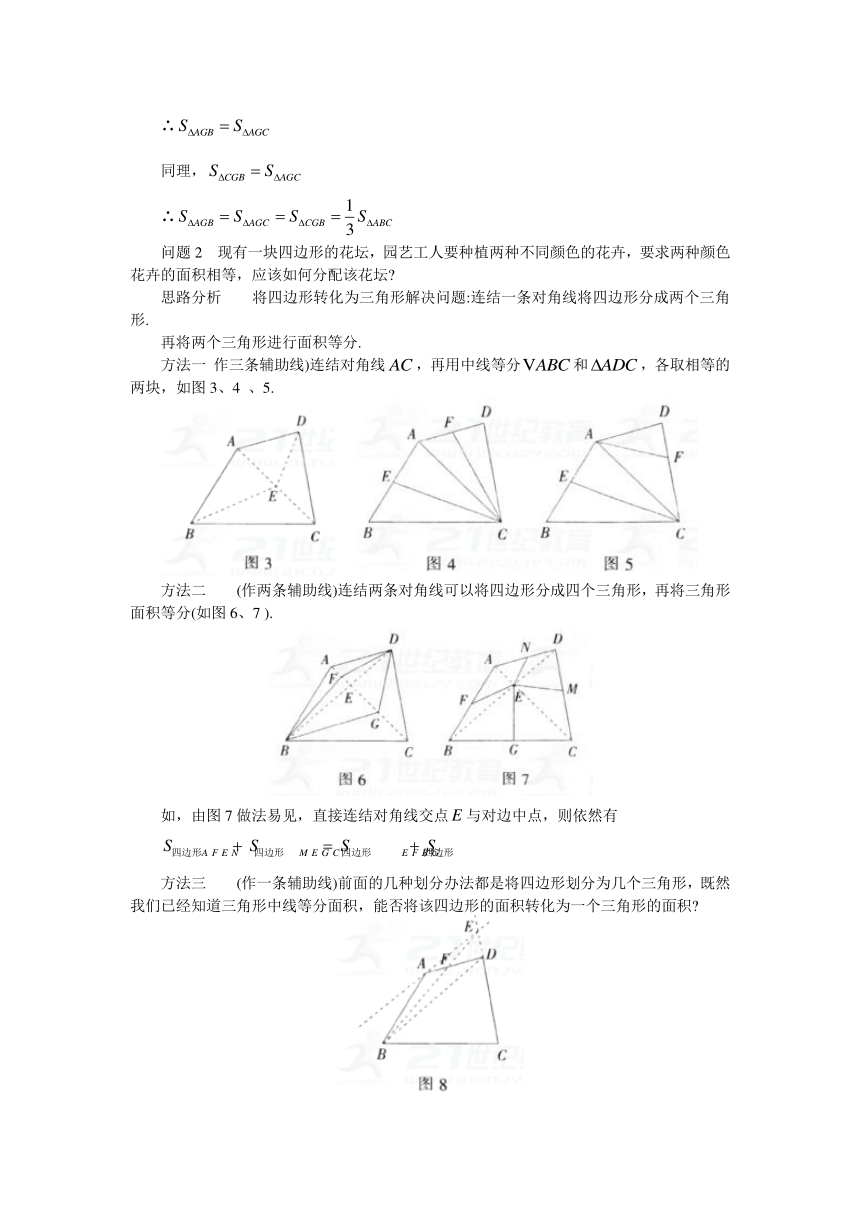
现有一块四边形的花坛,园艺工人要种植两种不同颜色的花卉,要求两种颜色花卉的面积相等,应该如何分配该花坛
思路分析
将四边形转化为三角形解决问题:连结一条对角线将四边形分成两个三角形.
再将两个三角形进行面积等分.
方法一
作三条辅助线)连结对角线,再用中线等分和,各取相等的两块,如图3、4
、5.
方法二
(作两条辅助线)连结两条对角线可以将四边形分成四个三角形,再将三角形面积等分(如图6、7
).
如,由图7做法易见,直接连结对角线交点与对边中点,则依然有
方法三
(作一条辅助线)前面的几种划分办法都是将四边形划分为几个三角形,既然我们已经知道三角形中线等分面积,能否将该四边形的面积转化为一个三角形的面积
如图8,过点作的平行线,由等底等高得出和的面积相等,则把四边形问题转化为三角形问题,再由中线等分面积此题就解决了.
点评
利用三角形中线等分三角形的面积体现了线段关系与三角形面积关系的相互转化,用代数方法解决了几何问题,同时多边形等分面积的问题转化为三角形问题也体现了转化的思想方法.
二、借助几何模型计算图形的面积
问题3
如图9所示:任意四边形,是中点,是中点,已知四边形面积是,则阴影部分的面积是
.
思路分析
首先根据是中点,可得和的面积相等,然后根据是中点,可得三角形和三角形的面积相等,进而判断出空白部分的面积等与阴影部分的面积;最后用四边形面积除以2,求出阴影部分的面积.
问题4
如图10,长方形的长为,宽为,、分别是和的中点,、交于点,求四边形的面积.
思路分析
因为、分别是和中点,则连结后,可知、分别是、的中线.
而由
可得
所以、、、的面积相等,且等于
因此,
问题5
在如图11至图13中,的面积为.
(1如图11,延长的边到点,使,连结.
若的面积为,则
(用含的代数式表示).
(2)如图12,延长的边到点,延长边到点,使,,连结.若的面积为,则
(用含的代数式表示),并说明理由.
(3)在图12的基础上延长到点,使,连结,得到(如图13).若阴影部分的面积为,则
(用含的代数式表示).
发现:像上面那样,将各边均顺次延长一倍,连结所得端点,得到
(如图14),此时,我们称向外扩展了一次.可以发现,扩展一次后得到的的面积是原来面积的
倍.
(4)应用:去年在面积为10m2的空地上栽种了某种花卉.今年准备扩大种植规模,把向外进行两次扩展,第一次由扩展成,第二次由扩展成(如图14).求这两次扩展的区域(即阴影部分)面积共为多少m2?
思路分析
从图11可以发现就是的中线,图12通过连接,可得到的中线,后面扩展的部分都可以通过这样的方法得到三角形的中线,从而求出扩展部分的面积,发现规律.
(1)由,可知就是的中线,中线将的分成两个三角形、,这两个三角形等底等高,所以它们的面积相等,所以.
(2)若连结,则就是的中线,中线将分成、它们的面积相等,所以.
(3)根据以上分析,可知、、的面积都为,所以.
发现:由题意可知扩展一次后的的面积是;即扩展一次后的的面积是原来面积的7倍.
应用由以上分析可知扩展一次后,扩展二次后,扩展三次后.拓展:
(
m2)
点评
巧求图形面积的方法是,从一个简单的图形入手,逐步探索出有关复杂图形的相关结论,这是我们研究数学问题的一种思想方法,即从特殊到一般的思想.我们在平时的学习中,要注意让学生领会数学思想和方法,使学生的思维不断升华.
三、借助几何模型求代数式的值
问题6
求的值.
问题7
请你利用问题6中的这个几何图形求的值.
思路分析
由数据的特征:后面的数为前面一个数的,联想到将三角形的面积不断的平分,所以可以构造如图15的图形进行求解.如图15,设大三角形的面积为1,然后不断的按顺序作出各个三角形的中线,根据三角形的中线把它分成两个面积相等的三角形可知,图中三角形除了最后一个小三角形,其余部分的面积为
∴
点评
数学是研究数量关系与空间形式的科学.而图形可以帮助我们发现、描述研究的问题,可以帮助我们寻求解决问题的思路,可以帮助我们理解和记忆得到的结果.几何直观就是依托、利用图形进行数学的思考和想象.本题虽然是一道代数计算题,但是仅仅从数的角度去计算比较困难.而借助几何模型,让学生更容易接受并运用数学知识去思考问题,形成几何直观能力,这也是数形结合思想的作用.
【基本模型】
如图1,线段是中线,则有
分析
过点作,垂足为,根据等底等高,有
∵
∴
三角形的中线由等底等高把分成两个面积相等的三角形.利用这模型,可以解决许多有关多边形面积的问题.
一、借助几何模型进行图形的分割
问题1
园艺工人要将一块三角形花坛分成三个面积相等的小三角形,分别种植三种不同的花卉,应该如何分配该花坛
思路分析
可以把三角形先三等分,再把其中一个再两等分,所以联想到作三角形的中线.具体方法:利用中线等分三角形面积中等底等高的思想方法,先将三角形一边进行三等分,连结对面顶点及其中一个三等分点,将三角形面积分成1:2,再将两份的进行二等分.
在划分方法中有一个图形不同于其它图形,单独来研究一下具体做法:
如图2,作三边上的中线交于点,则、、为分割线
证明
∵是中边的中线
∴
同理,
∴
∴
同理,
∴
问题2
现有一块四边形的花坛,园艺工人要种植两种不同颜色的花卉,要求两种颜色花卉的面积相等,应该如何分配该花坛
思路分析
将四边形转化为三角形解决问题:连结一条对角线将四边形分成两个三角形.
再将两个三角形进行面积等分.
方法一
作三条辅助线)连结对角线,再用中线等分和,各取相等的两块,如图3、4
、5.
方法二
(作两条辅助线)连结两条对角线可以将四边形分成四个三角形,再将三角形面积等分(如图6、7
).
如,由图7做法易见,直接连结对角线交点与对边中点,则依然有
方法三
(作一条辅助线)前面的几种划分办法都是将四边形划分为几个三角形,既然我们已经知道三角形中线等分面积,能否将该四边形的面积转化为一个三角形的面积
如图8,过点作的平行线,由等底等高得出和的面积相等,则把四边形问题转化为三角形问题,再由中线等分面积此题就解决了.
点评
利用三角形中线等分三角形的面积体现了线段关系与三角形面积关系的相互转化,用代数方法解决了几何问题,同时多边形等分面积的问题转化为三角形问题也体现了转化的思想方法.
二、借助几何模型计算图形的面积
问题3
如图9所示:任意四边形,是中点,是中点,已知四边形面积是,则阴影部分的面积是
.
思路分析
首先根据是中点,可得和的面积相等,然后根据是中点,可得三角形和三角形的面积相等,进而判断出空白部分的面积等与阴影部分的面积;最后用四边形面积除以2,求出阴影部分的面积.
问题4
如图10,长方形的长为,宽为,、分别是和的中点,、交于点,求四边形的面积.
思路分析
因为、分别是和中点,则连结后,可知、分别是、的中线.
而由
可得
所以、、、的面积相等,且等于
因此,
问题5
在如图11至图13中,的面积为.
(1如图11,延长的边到点,使,连结.
若的面积为,则
(用含的代数式表示).
(2)如图12,延长的边到点,延长边到点,使,,连结.若的面积为,则
(用含的代数式表示),并说明理由.
(3)在图12的基础上延长到点,使,连结,得到(如图13).若阴影部分的面积为,则
(用含的代数式表示).
发现:像上面那样,将各边均顺次延长一倍,连结所得端点,得到
(如图14),此时,我们称向外扩展了一次.可以发现,扩展一次后得到的的面积是原来面积的
倍.
(4)应用:去年在面积为10m2的空地上栽种了某种花卉.今年准备扩大种植规模,把向外进行两次扩展,第一次由扩展成,第二次由扩展成(如图14).求这两次扩展的区域(即阴影部分)面积共为多少m2?
思路分析
从图11可以发现就是的中线,图12通过连接,可得到的中线,后面扩展的部分都可以通过这样的方法得到三角形的中线,从而求出扩展部分的面积,发现规律.
(1)由,可知就是的中线,中线将的分成两个三角形、,这两个三角形等底等高,所以它们的面积相等,所以.
(2)若连结,则就是的中线,中线将分成、它们的面积相等,所以.
(3)根据以上分析,可知、、的面积都为,所以.
发现:由题意可知扩展一次后的的面积是;即扩展一次后的的面积是原来面积的7倍.
应用由以上分析可知扩展一次后,扩展二次后,扩展三次后.拓展:
(
m2)
点评
巧求图形面积的方法是,从一个简单的图形入手,逐步探索出有关复杂图形的相关结论,这是我们研究数学问题的一种思想方法,即从特殊到一般的思想.我们在平时的学习中,要注意让学生领会数学思想和方法,使学生的思维不断升华.
三、借助几何模型求代数式的值
问题6
求的值.
问题7
请你利用问题6中的这个几何图形求的值.
思路分析
由数据的特征:后面的数为前面一个数的,联想到将三角形的面积不断的平分,所以可以构造如图15的图形进行求解.如图15,设大三角形的面积为1,然后不断的按顺序作出各个三角形的中线,根据三角形的中线把它分成两个面积相等的三角形可知,图中三角形除了最后一个小三角形,其余部分的面积为
∴
点评
数学是研究数量关系与空间形式的科学.而图形可以帮助我们发现、描述研究的问题,可以帮助我们寻求解决问题的思路,可以帮助我们理解和记忆得到的结果.几何直观就是依托、利用图形进行数学的思考和想象.本题虽然是一道代数计算题,但是仅仅从数的角度去计算比较困难.而借助几何模型,让学生更容易接受并运用数学知识去思考问题,形成几何直观能力,这也是数形结合思想的作用.
同课章节目录
