第三章 圆单元检测A
图片预览




文档简介
九年级数学下册第三章《圆》单元检测A
一.选择题
1.如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )21世纪教育网版权所有
A.2<r< B.<r≤3 C.<r<5 D.5<r<
2.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
3.如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
A.AB=AD B.BC=CD C. D.∠BCA=∠DCA
4.如图,在⊙O中,半径OC与弦AB垂直于点D,且AB=8,OC=5,则CD的长是( )
A.3 B.2.5 C.2 D.1
5.如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
A.10cm B.16cm C.24cm D.26cm
6.如图,⊙O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )
A.43° B.35° C.34° D.44°
7.如图,四边形ABCD是⊙O的内接四边形,AD与BC的延长线交于点E,BA与CD的延长线交于点F,∠DCE=80°,∠F=25°,则∠E的度数为( )
A.55° B.50° C.45° D.40°
8.以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )
A.0≤b<2 B.﹣2 C.﹣22 D.﹣2<b<2
9.已知一个三角形的三边长分别为5、7、8,则其内切圆的半径为( )
A. B. C. D.
10.如图,⊙O的半径为6,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC与∠BOC互补,则线段BC的长为( )21教育网
A. B.3 C. D.6
11.如图,AB是⊙O的直径,直线DA与⊙O相切于点A,DO交⊙O于点C,连接BC,若∠ABC=21°,则∠ADC的度数为( )
A.46° B.47° C.48° D.49°
12.如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧的长等于( )
A. B. C. D.
二.填空题
13.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为弧BD的中点,若∠DAB=40°,则∠ABC= .
14.如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为 .
15.如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB= .
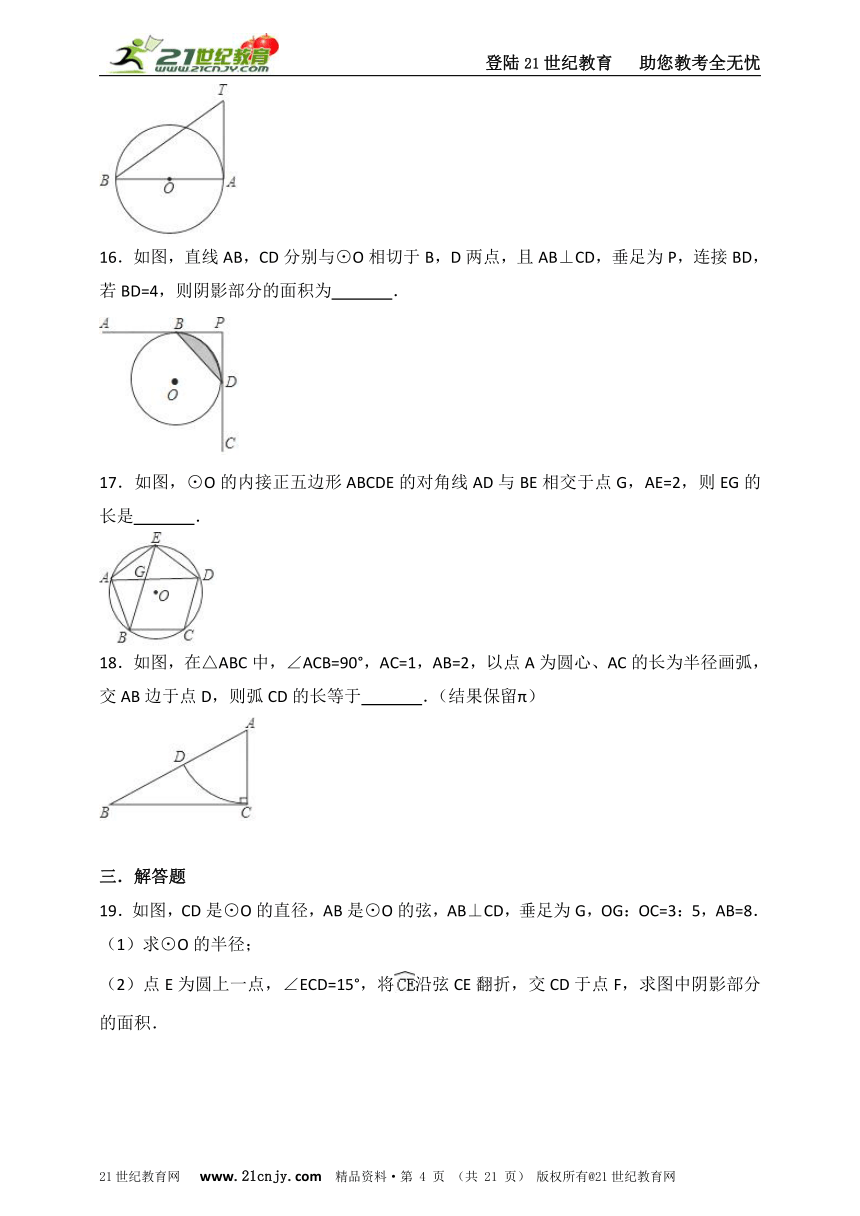
16.如图,直线AB,CD分别与⊙O相切于B,D两点,且AB⊥CD,垂足为P,连接BD,若BD=4,则阴影部分的面积为 .
17.如图,⊙O的内接正五边形ABCDE的对角线AD与BE相交于点G,AE=2,则EG的长是 .
18.如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于 .(结果保留π)
三.解答题
19.如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.
(1)求⊙O的半径;
(2)点E为圆上一点,∠ECD=15°,将沿弦CE翻折,交CD于点F,求图中阴影部分的面积.
20.如图,⊙O的直径AB=12cm,C为AB延长线上一点,CP与⊙O相切于点P,过点B作弦BD∥CP,连接PD.
(1)求证:点P为的中点;
(2)若∠C=∠D,求四边形BCPD的面积.
21.如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.
(1)求证:∠1=∠F.
(2)若sinB=,EF=2,求CD的长.
22.如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.
(1)求证:AP=AB;
(2)若OB=4,AB=3,求线段BP的长.
23.如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
(1)求证:四边形AECD为平行四边形;
(2)连接CO,求证:CO平分∠BCE.
24.如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.
答案与解析
一.选择题
1.【分析】利用勾股定理求出各格点到点A的距离,结合点与圆的位置关系,即可得出结论.
【解答】解:给各点标上字母,如图所示.
AB==2,AC=AD==,AE==3,AF==,AG=AM=AN==5,
∴<r≤3时,以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内.
故选B.
2.【分析】根据正多边形的中心角的度数即可得到结论.
【解答】解:∵正三角形一条边所对的圆心角是360°÷3=120°,
正方形一条边所对的圆心角是360°÷4=90°,
正五边形一条边所对的圆心角是360°÷5=72°,
正六边形一条边所对的圆心角是360°÷6=60°,
∴一条边所对的圆心角最大的图形是正三角形,
故选A.
3.【分析】根据圆心角、弧、弦的关系对各选项进行逐一判断即可.
【解答】解:A、∵∠ACB与∠ACD的大小关系不确定,∴AB与AD不一定相等,故本选项错误;
B、∵AC平分∠BAD,∴∠BAC=∠DAC,∴BC=CD,故本选项正确;
C、∵∠ACB与∠ACD的大小关系不确定,∴与不一定相等,故本选项错误;
D、∠BCA与∠DCA的大小关系不确定,故本选项错误.
故选B.
4.【分析】根据垂径定理以及勾股定理即可求答案.
【解答】解:连接OA,
设CD=x,
∵OA=OC=5,
∴OD=5﹣x,
∵OC⊥AB,
∴由垂径定理可知:AB=4,
由勾股定理可知:52=42+(5﹣x)2
∴x=2,
∴CD=2,
故选(C)
5.【分析】首先构造直角三角形,再利用勾股定理得出BC的长,进而根据垂径定理得出答案.
【解答】解:如图,过O作OD⊥AB于C,交⊙O于D,
∵CD=8,OD=13,
∴OC=5,
又∵OB=13,
∴Rt△BCO中,BC==12,
∴AB=2BC=24.
故选:C.
6.【分析】由同弧所对的圆周角相等求得∠A=∠D=42°,然后根据三角形外角的性质即可得到结论.
【解答】解:∵∠D=∠A=42°,
∴∠B=∠APD﹣∠D=35°,
故选B.
7.【分析】根据三角形的外角的性质求出∠B,根据圆内接四边形的性质和三角形内角和定理计算即可.
【解答】解:∠B=∠DCE﹣∠F=55°,
∵四边形ABCD是⊙O的内接四边形,
∴∠EDC=∠B=55°,
∴∠E=180°﹣∠DCE﹣∠EDC=45°,
故选:C.
8.【分析】求出直线y=﹣x+b与圆相切,且函数经过一、二、四象限,和当直线y=﹣x+b与圆相切,且函数经过二、三、四象限时b的值,则相交时b的值在相切时的两个b的值之间.21cnjy.com
【解答】解:当直线y=﹣x+b与圆相切,且函数经过一、二、四象限时,如图.
在y=﹣x+b中,令x=0时,y=b,则与y轴的交点是(0,b),
当y=0时,x=b,则A的交点是(b,0),
则OA=OB,即△OAB是等腰直角三角形.
连接圆心O和切点C.则OC=2.
则OB=OC=2.即b=2;
同理,当直线y=﹣x+b与圆相切,且函数经过二、三、四象限时,b=﹣2.
则若直线y=﹣x+b与⊙O相交,则b的取值范围是﹣2<b<2.
故选D.
9.【分析】如图,AB=7,BC=5,AC=8,内切圆的半径为r,切点为G、E、F,作AD⊥BC于D,设BD=x,则CD=5﹣x.由AD2=AB2﹣BD2=AC2﹣CD2,可得72﹣x2=82﹣(5﹣x)2,解得x=1,推出AD=4,由?BC?AD=(AB+BC+AC)?r,列出方程即可解决问题.
【解答】解:如图,AB=7,BC=5,AC=8,内切圆的半径为r,切点为G、E、F,作AD⊥BC于D,设BD=x,则CD=5﹣x.www.21-cn-jy.com
由勾股定理可知:AD2=AB2﹣BD2=AC2﹣CD2,
即72﹣x2=82﹣(5﹣x)2,解得x=1,
∴AD=4,
∵?BC?AD=(AB+BC+AC)?r,
×5×4=×20×r,
∴r=,
故选C
10.【分析】作弦心距OD,先根据已知求出∠BOC=120°,由等腰三角形三线合一的性质得:∠DOC=∠BOC=60°,利用30°角所对的直角边是斜边的一半可求得OD的长,根据勾股定理得DC的长,最后利用垂径定理得出结论.2·1·c·n·j·y
【解答】解:∵∠BAC与∠BOC互补,
∴∠BAC+∠BOC=180°,
∵∠BAC=∠BOC,
∴∠BOC=120°,
过O作OD⊥BC,垂足为D,
∴BD=CD,
∵OB=OC,
∴OD平分∠BOC,
∴∠DOC=∠BOC=60°,
∴∠OCD=90°﹣60°=30°,
在Rt△DOC中,OC=6,
∴OD=3,
∴DC=3,
∴BC=2DC=6,
故选:C.
11.【分析】根据等边对等角可得∠B=∠BCO,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AOD=∠B+∠BCO,根据切线的性质可得∠OAD=90°,然后根据直角三角形两锐角互余求解即可.21·cn·jy·com
【解答】解:∵OB=OC,
∴∠B=∠BCO=21°,
∴∠AOD=∠B+∠BCO=21°+21°=42°,
∵AB是⊙O的直径,直线DA与⊙O相切与点A,
∴∠OAD=90°,
∴∠ADC=90°﹣∠AOD=90°﹣42°=48°.
故选C.
12.【分析】连接OB、OC,利用圆周角定理求得∠BOC=60°,然后利用弧长公式l=来计算劣弧的长.【来源:21·世纪·教育·网】
【解答】解:如图,连接OB、OC,
∵∠BAC=30°,
∴∠BOC=2∠BAC=60°,
又OB=OC,
∴△OBC是等边三角形,
∴BC=OB=OC=2,
∴劣弧的长为:=.
故选:A.
二.填空题
13.【分析】连接AC,根据圆周角定理得到∠CAB=∠DAB=20°,∠ACB=90°,计算即可.www-2-1-cnjy-com
【解答】解:连接AC,
∵点C为弧BD的中点,
∴∠CAB=∠DAB=20°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ABC=70°,
故答案为:70°.
14.【分析】由等边三角形的性质得出∠ABC=∠BAC=60°,AC=AB=2,求出∠APC=120°,当PB⊥AC时,PB长度最小,设垂足为D,此时PA=PC,由等边三角形的性质得出AD=CD=AC=1,∠PAC=∠ACP=30°,∠ABD=∠ABC=30°,求出PD=AD?tan30°=AD=,BD=AD=,即可得出答案.2-1-c-n-j-y
【解答】解:∵△ABC是等边三角形,
∴∠ABC=∠BAC=60°,AC=AB=2,
∵∠PAB=∠ACP,
∴∠PAC+∠ACP=60°,
∴∠APC=120°,
∴点P的运动轨迹是,
当O、P、B共线时,PB长度最小,设OB交AC于D,如图所示:
此时PA=PC,OB⊥AC,
则AD=CD=AC=1,∠PAC=∠ACP=30°,∠ABD=∠ABC=30°,
∴PD=AD?tan30°=AD=,BD=AD=,
∴PB=BD﹣PD=﹣=;
故答案为:.
15.【分析】根据切线的性质即可求出答案.
【解答】解:∵AT切⊙O于点A,AB是⊙O的直径,
∴∠BAT=90°,
∵∠ABT=40°,
∴∠ATB=50°,
故答案为:50°
16.【分析】连接OB、OD,根据切线的性质和垂直得出∠OBP=∠P=∠ODP=90°,求出四边形BODP是正方形,根据正方形的性质得出∠BOD=90°,求出扇形BOD和△BOD的面积,即可得出答案.【出处:21教育名师】
【解答】解:
连接OB、OD,
∵直线AB,CD分别与⊙O相切于B,D两点,AB⊥CD,
∴∠OBP=∠P=∠ODP=90°,
∵OB=OD,
∴四边形BODP是正方形,
∴∠BOD=90°,
∵BD=4,
∴OB==2,
∴阴影部分的面积S=S扇形BOD﹣S△BOD=﹣=2π﹣4,
故答案为:2π﹣4.
17.【分析】在⊙O的内接正五边形ABCDE中,设EG=x,易知:∠AEB=∠ABE=∠EAG=36°,∠BAG=∠AGB=72°,推出AB=BG=AE=2,由△AEG∽△BEA,可得AE2=EG?EB,可得22=x(x+2),解方程即可.【来源:21cnj*y.co*m】
【解答】解:在⊙O的内接正五边形ABCDE中,设EG=x,
易知:∠AEB=∠ABE=∠EAG=36°,
∠BAG=∠AGB=72°,
∴AB=BG=AE=2,
∵∠AEG=∠AEB,∠EAG=∠EBA,
∴△AEG∽△BEA,
∴AE2=EG?EB,
∴22=x(x+2),
解得x=﹣1+或﹣1﹣,
∴EG=﹣1,
故答案为﹣1.
18.【分析】先根据ACB=90°,AC=1,AB=2,得到∠ABC=30°,进而得出∠A=60°,再根据AC=1,即可得到弧CD的长.21教育名师原创作品
【解答】解:∵∠ACB=90°,AC=1,AB=2,
∴∠ABC=30°,
∴∠A=60°,
又∵AC=1,
∴弧CD的长为=,
故答案为:.
三.解答题
19.【分析】(1)根据AB⊥CD,垂足为G,OG:OC=3:5,AB=8,可以求得⊙O的半径;
(2)要求阴影部分的面积只要做出合适的辅助线,然后利用锐角三角函数、扇形的面积和三角形的面积即可解答本题.
【解答】解:(1)连接AO,如右图1所示,
∵CD为⊙O的直径,AB⊥CD,AB=8,
∴AG==4,
∵OG:OC=3:5,AB⊥CD,垂足为G,
∴设⊙O的半径为5k,则OG=3k,
∴(3k)2+42=(5k)2,
解得,k=1或k=﹣1(舍去),
∴5k=5,
即⊙O的半径是5;
(2)如图2所示,将阴影部分沿CE翻折,点F的对应点为M,
∵∠ECD=15°,由对称性可知,∠DCM=30°,S阴影=S弓形CBM,
连接OM,则∠MOD=60°,
∴∠MOC=120°,
过点M作MN⊥CD于点N,
∴MN=MO?sin60°=5×,
∴S阴影=S扇形OMC﹣S△OMC==,
即图中阴影部分的面积是:.
20.【分析】(1)连接OP,根据切线的性质得到PC⊥OP,根据平行线的性质得到BD⊥OP,根据垂径定理即可得到结论;21*cnjy*com
(2)根据圆周角定理得到∠POB=2∠D,根据三角形的内角和得到∠C=30°,推出四边形BCPD是平行四边形,于是得到结论.
【解答】(1)证明:连接OP,
∵CP与⊙O相切于点P,
∴PC⊥OP,
∴∠OPC=90度,
∵BD∥CP,
∴∠OEP=OPC=90度,
∴BD⊥OP,
∴点P为的中点.
(2)解:∵∠C=∠D,
∵∠POB=2∠D,
∴∠POB=2∠C,
∵∠CPO=90°,
∴∠C=30°,
∵BD∥CP,
∴∠C=∠DBA,
∴∠D=∠DBA,
∴BC∥PD,
∴四边形BCPD是平行四边形,
∵PO=AB=6,
∴PC=6,
∵∠ABD=∠C=30°,
∴OE=OB=3,
∴PE=3,
∴四边形BCPD的面积=PC?PE=6×3=18.
21.【分析】(1)连接DE,由BD是⊙O的直径,得到∠DEB=90°,由于E是AB的中点,得到DA=DB,根据等腰三角形的性质得到∠1=∠B等量代换即可得到结论;
(2)根据等腰三角形的判定定理得到AE=EF=2,推出AB=2AE=4,在Rt△ABC中,根据勾股定理得到BC==8,设CD=x,则AD=BD=8﹣x,根据勾股定理列方程即可得到结论.【版权所有:21教育】
【解答】解:(1)证明:连接DE,
∵BD是⊙O的直径,
∴∠DEB=90°,
∵E是AB的中点,
∴DA=DB,
∴∠1=∠B,
∵∠B=∠F,
∴∠1=∠F;
(2)∵∠1=∠F,
∴AE=EF=2,
∴AB=2AE=4,
在Rt△ABC中,AC=AB?sinB=4,
∴BC==8,
设CD=x,则AD=BD=8﹣x,
∵AC2+CD2=AD2,
即42+x2=(8﹣x)2,
∴x=3,即CD=3.
22.【分析】(1)欲证明AP=AB,只要证明∠APB=∠ABP即可;
(2)作OH⊥BC于H.在Rt△POC中,求出OP、PC、OH、CH即可解决问题.
【解答】(1)证明:∵OC=OB,
∴∠OCB=∠OBC,
∵AB是⊙O的切线,
∴OB⊥AB,
∴∠OBA=90°,
∴∠ABP+∠OBC=90°,
∵OC⊥AO,
∴∠AOC=90°,
∴∠OCB+∠CPO=90°,
∵∠APB=∠CPO,
∴∠APB=∠ABP,
∴AP=AB.
(2)解:作OH⊥BC于H.
在Rt△OAB中,∵OB=4,AB=3,
∴OA==5,
∵AP=AB=3,
∴PO=2.
在Rt△POC中,PC==2,
∵?PC?OH=?OC?OP,
∴OH==,
∴CH==,
∵OH⊥BC,
∴CH=BH,
∴BC=2CH=,
∴PB=BC﹣PC=﹣2=.
23.【分析】(1)根据圆周角定理得到∠B=∠E,得到∠E=∠D,根据平行线的判定和性质定理得到AE∥CD,证明结论;21·世纪*教育网
(2)作OM⊥BC于M,ON⊥CE于N,根据垂径定理、角平分线的判定定理证明.
【解答】证明:(1)由圆周角定理得,∠B=∠E,又∠B=∠D,
∴∠E=∠D,
∵CE∥AD,
∴∠D+∠ECD=180°,
∴∠E+∠ECD=180°,
∴AE∥CD,
∴四边形AECD为平行四边形;
(2)作OM⊥BC于M,ON⊥CE于N,
∵四边形AECD为平行四边形,
∴AD=CE,又AD=BC,
∴CE=CB,
∴OM=ON,又OM⊥BC,ON⊥CE,
∴CO平分∠BCE.
24.【分析】(1)直线DE与圆O相切,理由如下:连接OD,由OD=OA,利用等边对等角得到一对角相等,等量代换得到∠ODE为直角,即可得证;21*cnjy*com
(2)连接OE,设DE=x,则EB=ED=x,CE=8﹣x,在直角三角形OCE中,利用勾股定理列出关于x的方程,求出方程的得到x的值,即可确定出DE的长.
【解答】解:(1)直线DE与⊙O相切,理由如下:
连接OD,
∵OD=OA,
∴∠A=∠ODA,
∵EF是BD的垂直平分线,
∴EB=ED,
∴∠B=∠EDB,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=180°﹣90°=90°,
∴直线DE与⊙O相切;
(2)连接OE,
设DE=x,则EB=ED=x,CE=8﹣x,
∵∠C=∠ODE=90°,
∴OC2+CE2=OE2=OD2+DE2,
∴42+(8﹣x)2=22+x2,
解得:x=4.75,
则DE=4.75.
一.选择题
1.如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )21世纪教育网版权所有
A.2<r< B.<r≤3 C.<r<5 D.5<r<
2.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
3.如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
A.AB=AD B.BC=CD C. D.∠BCA=∠DCA
4.如图,在⊙O中,半径OC与弦AB垂直于点D,且AB=8,OC=5,则CD的长是( )
A.3 B.2.5 C.2 D.1
5.如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
A.10cm B.16cm C.24cm D.26cm
6.如图,⊙O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )
A.43° B.35° C.34° D.44°
7.如图,四边形ABCD是⊙O的内接四边形,AD与BC的延长线交于点E,BA与CD的延长线交于点F,∠DCE=80°,∠F=25°,则∠E的度数为( )
A.55° B.50° C.45° D.40°
8.以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )
A.0≤b<2 B.﹣2 C.﹣22 D.﹣2<b<2
9.已知一个三角形的三边长分别为5、7、8,则其内切圆的半径为( )
A. B. C. D.
10.如图,⊙O的半径为6,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC与∠BOC互补,则线段BC的长为( )21教育网
A. B.3 C. D.6
11.如图,AB是⊙O的直径,直线DA与⊙O相切于点A,DO交⊙O于点C,连接BC,若∠ABC=21°,则∠ADC的度数为( )
A.46° B.47° C.48° D.49°
12.如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧的长等于( )
A. B. C. D.
二.填空题
13.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为弧BD的中点,若∠DAB=40°,则∠ABC= .
14.如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为 .
15.如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB= .
16.如图,直线AB,CD分别与⊙O相切于B,D两点,且AB⊥CD,垂足为P,连接BD,若BD=4,则阴影部分的面积为 .
17.如图,⊙O的内接正五边形ABCDE的对角线AD与BE相交于点G,AE=2,则EG的长是 .
18.如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于 .(结果保留π)
三.解答题
19.如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.
(1)求⊙O的半径;
(2)点E为圆上一点,∠ECD=15°,将沿弦CE翻折,交CD于点F,求图中阴影部分的面积.
20.如图,⊙O的直径AB=12cm,C为AB延长线上一点,CP与⊙O相切于点P,过点B作弦BD∥CP,连接PD.
(1)求证:点P为的中点;
(2)若∠C=∠D,求四边形BCPD的面积.
21.如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.
(1)求证:∠1=∠F.
(2)若sinB=,EF=2,求CD的长.
22.如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.
(1)求证:AP=AB;
(2)若OB=4,AB=3,求线段BP的长.
23.如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
(1)求证:四边形AECD为平行四边形;
(2)连接CO,求证:CO平分∠BCE.
24.如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.
答案与解析
一.选择题
1.【分析】利用勾股定理求出各格点到点A的距离,结合点与圆的位置关系,即可得出结论.
【解答】解:给各点标上字母,如图所示.
AB==2,AC=AD==,AE==3,AF==,AG=AM=AN==5,
∴<r≤3时,以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内.
故选B.
2.【分析】根据正多边形的中心角的度数即可得到结论.
【解答】解:∵正三角形一条边所对的圆心角是360°÷3=120°,
正方形一条边所对的圆心角是360°÷4=90°,
正五边形一条边所对的圆心角是360°÷5=72°,
正六边形一条边所对的圆心角是360°÷6=60°,
∴一条边所对的圆心角最大的图形是正三角形,
故选A.
3.【分析】根据圆心角、弧、弦的关系对各选项进行逐一判断即可.
【解答】解:A、∵∠ACB与∠ACD的大小关系不确定,∴AB与AD不一定相等,故本选项错误;
B、∵AC平分∠BAD,∴∠BAC=∠DAC,∴BC=CD,故本选项正确;
C、∵∠ACB与∠ACD的大小关系不确定,∴与不一定相等,故本选项错误;
D、∠BCA与∠DCA的大小关系不确定,故本选项错误.
故选B.
4.【分析】根据垂径定理以及勾股定理即可求答案.
【解答】解:连接OA,
设CD=x,
∵OA=OC=5,
∴OD=5﹣x,
∵OC⊥AB,
∴由垂径定理可知:AB=4,
由勾股定理可知:52=42+(5﹣x)2
∴x=2,
∴CD=2,
故选(C)
5.【分析】首先构造直角三角形,再利用勾股定理得出BC的长,进而根据垂径定理得出答案.
【解答】解:如图,过O作OD⊥AB于C,交⊙O于D,
∵CD=8,OD=13,
∴OC=5,
又∵OB=13,
∴Rt△BCO中,BC==12,
∴AB=2BC=24.
故选:C.
6.【分析】由同弧所对的圆周角相等求得∠A=∠D=42°,然后根据三角形外角的性质即可得到结论.
【解答】解:∵∠D=∠A=42°,
∴∠B=∠APD﹣∠D=35°,
故选B.
7.【分析】根据三角形的外角的性质求出∠B,根据圆内接四边形的性质和三角形内角和定理计算即可.
【解答】解:∠B=∠DCE﹣∠F=55°,
∵四边形ABCD是⊙O的内接四边形,
∴∠EDC=∠B=55°,
∴∠E=180°﹣∠DCE﹣∠EDC=45°,
故选:C.
8.【分析】求出直线y=﹣x+b与圆相切,且函数经过一、二、四象限,和当直线y=﹣x+b与圆相切,且函数经过二、三、四象限时b的值,则相交时b的值在相切时的两个b的值之间.21cnjy.com
【解答】解:当直线y=﹣x+b与圆相切,且函数经过一、二、四象限时,如图.
在y=﹣x+b中,令x=0时,y=b,则与y轴的交点是(0,b),
当y=0时,x=b,则A的交点是(b,0),
则OA=OB,即△OAB是等腰直角三角形.
连接圆心O和切点C.则OC=2.
则OB=OC=2.即b=2;
同理,当直线y=﹣x+b与圆相切,且函数经过二、三、四象限时,b=﹣2.
则若直线y=﹣x+b与⊙O相交,则b的取值范围是﹣2<b<2.
故选D.
9.【分析】如图,AB=7,BC=5,AC=8,内切圆的半径为r,切点为G、E、F,作AD⊥BC于D,设BD=x,则CD=5﹣x.由AD2=AB2﹣BD2=AC2﹣CD2,可得72﹣x2=82﹣(5﹣x)2,解得x=1,推出AD=4,由?BC?AD=(AB+BC+AC)?r,列出方程即可解决问题.
【解答】解:如图,AB=7,BC=5,AC=8,内切圆的半径为r,切点为G、E、F,作AD⊥BC于D,设BD=x,则CD=5﹣x.www.21-cn-jy.com
由勾股定理可知:AD2=AB2﹣BD2=AC2﹣CD2,
即72﹣x2=82﹣(5﹣x)2,解得x=1,
∴AD=4,
∵?BC?AD=(AB+BC+AC)?r,
×5×4=×20×r,
∴r=,
故选C
10.【分析】作弦心距OD,先根据已知求出∠BOC=120°,由等腰三角形三线合一的性质得:∠DOC=∠BOC=60°,利用30°角所对的直角边是斜边的一半可求得OD的长,根据勾股定理得DC的长,最后利用垂径定理得出结论.2·1·c·n·j·y
【解答】解:∵∠BAC与∠BOC互补,
∴∠BAC+∠BOC=180°,
∵∠BAC=∠BOC,
∴∠BOC=120°,
过O作OD⊥BC,垂足为D,
∴BD=CD,
∵OB=OC,
∴OD平分∠BOC,
∴∠DOC=∠BOC=60°,
∴∠OCD=90°﹣60°=30°,
在Rt△DOC中,OC=6,
∴OD=3,
∴DC=3,
∴BC=2DC=6,
故选:C.
11.【分析】根据等边对等角可得∠B=∠BCO,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AOD=∠B+∠BCO,根据切线的性质可得∠OAD=90°,然后根据直角三角形两锐角互余求解即可.21·cn·jy·com
【解答】解:∵OB=OC,
∴∠B=∠BCO=21°,
∴∠AOD=∠B+∠BCO=21°+21°=42°,
∵AB是⊙O的直径,直线DA与⊙O相切与点A,
∴∠OAD=90°,
∴∠ADC=90°﹣∠AOD=90°﹣42°=48°.
故选C.
12.【分析】连接OB、OC,利用圆周角定理求得∠BOC=60°,然后利用弧长公式l=来计算劣弧的长.【来源:21·世纪·教育·网】
【解答】解:如图,连接OB、OC,
∵∠BAC=30°,
∴∠BOC=2∠BAC=60°,
又OB=OC,
∴△OBC是等边三角形,
∴BC=OB=OC=2,
∴劣弧的长为:=.
故选:A.
二.填空题
13.【分析】连接AC,根据圆周角定理得到∠CAB=∠DAB=20°,∠ACB=90°,计算即可.www-2-1-cnjy-com
【解答】解:连接AC,
∵点C为弧BD的中点,
∴∠CAB=∠DAB=20°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ABC=70°,
故答案为:70°.
14.【分析】由等边三角形的性质得出∠ABC=∠BAC=60°,AC=AB=2,求出∠APC=120°,当PB⊥AC时,PB长度最小,设垂足为D,此时PA=PC,由等边三角形的性质得出AD=CD=AC=1,∠PAC=∠ACP=30°,∠ABD=∠ABC=30°,求出PD=AD?tan30°=AD=,BD=AD=,即可得出答案.2-1-c-n-j-y
【解答】解:∵△ABC是等边三角形,
∴∠ABC=∠BAC=60°,AC=AB=2,
∵∠PAB=∠ACP,
∴∠PAC+∠ACP=60°,
∴∠APC=120°,
∴点P的运动轨迹是,
当O、P、B共线时,PB长度最小,设OB交AC于D,如图所示:
此时PA=PC,OB⊥AC,
则AD=CD=AC=1,∠PAC=∠ACP=30°,∠ABD=∠ABC=30°,
∴PD=AD?tan30°=AD=,BD=AD=,
∴PB=BD﹣PD=﹣=;
故答案为:.
15.【分析】根据切线的性质即可求出答案.
【解答】解:∵AT切⊙O于点A,AB是⊙O的直径,
∴∠BAT=90°,
∵∠ABT=40°,
∴∠ATB=50°,
故答案为:50°
16.【分析】连接OB、OD,根据切线的性质和垂直得出∠OBP=∠P=∠ODP=90°,求出四边形BODP是正方形,根据正方形的性质得出∠BOD=90°,求出扇形BOD和△BOD的面积,即可得出答案.【出处:21教育名师】
【解答】解:
连接OB、OD,
∵直线AB,CD分别与⊙O相切于B,D两点,AB⊥CD,
∴∠OBP=∠P=∠ODP=90°,
∵OB=OD,
∴四边形BODP是正方形,
∴∠BOD=90°,
∵BD=4,
∴OB==2,
∴阴影部分的面积S=S扇形BOD﹣S△BOD=﹣=2π﹣4,
故答案为:2π﹣4.
17.【分析】在⊙O的内接正五边形ABCDE中,设EG=x,易知:∠AEB=∠ABE=∠EAG=36°,∠BAG=∠AGB=72°,推出AB=BG=AE=2,由△AEG∽△BEA,可得AE2=EG?EB,可得22=x(x+2),解方程即可.【来源:21cnj*y.co*m】
【解答】解:在⊙O的内接正五边形ABCDE中,设EG=x,
易知:∠AEB=∠ABE=∠EAG=36°,
∠BAG=∠AGB=72°,
∴AB=BG=AE=2,
∵∠AEG=∠AEB,∠EAG=∠EBA,
∴△AEG∽△BEA,
∴AE2=EG?EB,
∴22=x(x+2),
解得x=﹣1+或﹣1﹣,
∴EG=﹣1,
故答案为﹣1.
18.【分析】先根据ACB=90°,AC=1,AB=2,得到∠ABC=30°,进而得出∠A=60°,再根据AC=1,即可得到弧CD的长.21教育名师原创作品
【解答】解:∵∠ACB=90°,AC=1,AB=2,
∴∠ABC=30°,
∴∠A=60°,
又∵AC=1,
∴弧CD的长为=,
故答案为:.
三.解答题
19.【分析】(1)根据AB⊥CD,垂足为G,OG:OC=3:5,AB=8,可以求得⊙O的半径;
(2)要求阴影部分的面积只要做出合适的辅助线,然后利用锐角三角函数、扇形的面积和三角形的面积即可解答本题.
【解答】解:(1)连接AO,如右图1所示,
∵CD为⊙O的直径,AB⊥CD,AB=8,
∴AG==4,
∵OG:OC=3:5,AB⊥CD,垂足为G,
∴设⊙O的半径为5k,则OG=3k,
∴(3k)2+42=(5k)2,
解得,k=1或k=﹣1(舍去),
∴5k=5,
即⊙O的半径是5;
(2)如图2所示,将阴影部分沿CE翻折,点F的对应点为M,
∵∠ECD=15°,由对称性可知,∠DCM=30°,S阴影=S弓形CBM,
连接OM,则∠MOD=60°,
∴∠MOC=120°,
过点M作MN⊥CD于点N,
∴MN=MO?sin60°=5×,
∴S阴影=S扇形OMC﹣S△OMC==,
即图中阴影部分的面积是:.
20.【分析】(1)连接OP,根据切线的性质得到PC⊥OP,根据平行线的性质得到BD⊥OP,根据垂径定理即可得到结论;21*cnjy*com
(2)根据圆周角定理得到∠POB=2∠D,根据三角形的内角和得到∠C=30°,推出四边形BCPD是平行四边形,于是得到结论.
【解答】(1)证明:连接OP,
∵CP与⊙O相切于点P,
∴PC⊥OP,
∴∠OPC=90度,
∵BD∥CP,
∴∠OEP=OPC=90度,
∴BD⊥OP,
∴点P为的中点.
(2)解:∵∠C=∠D,
∵∠POB=2∠D,
∴∠POB=2∠C,
∵∠CPO=90°,
∴∠C=30°,
∵BD∥CP,
∴∠C=∠DBA,
∴∠D=∠DBA,
∴BC∥PD,
∴四边形BCPD是平行四边形,
∵PO=AB=6,
∴PC=6,
∵∠ABD=∠C=30°,
∴OE=OB=3,
∴PE=3,
∴四边形BCPD的面积=PC?PE=6×3=18.
21.【分析】(1)连接DE,由BD是⊙O的直径,得到∠DEB=90°,由于E是AB的中点,得到DA=DB,根据等腰三角形的性质得到∠1=∠B等量代换即可得到结论;
(2)根据等腰三角形的判定定理得到AE=EF=2,推出AB=2AE=4,在Rt△ABC中,根据勾股定理得到BC==8,设CD=x,则AD=BD=8﹣x,根据勾股定理列方程即可得到结论.【版权所有:21教育】
【解答】解:(1)证明:连接DE,
∵BD是⊙O的直径,
∴∠DEB=90°,
∵E是AB的中点,
∴DA=DB,
∴∠1=∠B,
∵∠B=∠F,
∴∠1=∠F;
(2)∵∠1=∠F,
∴AE=EF=2,
∴AB=2AE=4,
在Rt△ABC中,AC=AB?sinB=4,
∴BC==8,
设CD=x,则AD=BD=8﹣x,
∵AC2+CD2=AD2,
即42+x2=(8﹣x)2,
∴x=3,即CD=3.
22.【分析】(1)欲证明AP=AB,只要证明∠APB=∠ABP即可;
(2)作OH⊥BC于H.在Rt△POC中,求出OP、PC、OH、CH即可解决问题.
【解答】(1)证明:∵OC=OB,
∴∠OCB=∠OBC,
∵AB是⊙O的切线,
∴OB⊥AB,
∴∠OBA=90°,
∴∠ABP+∠OBC=90°,
∵OC⊥AO,
∴∠AOC=90°,
∴∠OCB+∠CPO=90°,
∵∠APB=∠CPO,
∴∠APB=∠ABP,
∴AP=AB.
(2)解:作OH⊥BC于H.
在Rt△OAB中,∵OB=4,AB=3,
∴OA==5,
∵AP=AB=3,
∴PO=2.
在Rt△POC中,PC==2,
∵?PC?OH=?OC?OP,
∴OH==,
∴CH==,
∵OH⊥BC,
∴CH=BH,
∴BC=2CH=,
∴PB=BC﹣PC=﹣2=.
23.【分析】(1)根据圆周角定理得到∠B=∠E,得到∠E=∠D,根据平行线的判定和性质定理得到AE∥CD,证明结论;21·世纪*教育网
(2)作OM⊥BC于M,ON⊥CE于N,根据垂径定理、角平分线的判定定理证明.
【解答】证明:(1)由圆周角定理得,∠B=∠E,又∠B=∠D,
∴∠E=∠D,
∵CE∥AD,
∴∠D+∠ECD=180°,
∴∠E+∠ECD=180°,
∴AE∥CD,
∴四边形AECD为平行四边形;
(2)作OM⊥BC于M,ON⊥CE于N,
∵四边形AECD为平行四边形,
∴AD=CE,又AD=BC,
∴CE=CB,
∴OM=ON,又OM⊥BC,ON⊥CE,
∴CO平分∠BCE.
24.【分析】(1)直线DE与圆O相切,理由如下:连接OD,由OD=OA,利用等边对等角得到一对角相等,等量代换得到∠ODE为直角,即可得证;21*cnjy*com
(2)连接OE,设DE=x,则EB=ED=x,CE=8﹣x,在直角三角形OCE中,利用勾股定理列出关于x的方程,求出方程的得到x的值,即可确定出DE的长.
【解答】解:(1)直线DE与⊙O相切,理由如下:
连接OD,
∵OD=OA,
∴∠A=∠ODA,
∵EF是BD的垂直平分线,
∴EB=ED,
∴∠B=∠EDB,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=180°﹣90°=90°,
∴直线DE与⊙O相切;
(2)连接OE,
设DE=x,则EB=ED=x,CE=8﹣x,
∵∠C=∠ODE=90°,
∴OC2+CE2=OE2=OD2+DE2,
∴42+(8﹣x)2=22+x2,
解得:x=4.75,
则DE=4.75.
