北师大版九年级数学下册第三章 圆习题(含答案)
文档属性
| 名称 | 北师大版九年级数学下册第三章 圆习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-18 19:35:43 | ||
图片预览


文档简介
第三章 圆
3.1 圆
基础题
知识点1 圆的有关概念
1.下列说法正确的是(D)
A.半圆是弧,弧也是半圆
B.过圆上任意一点只能作一条弦,且这条弦是直径
C.弦是直径
D.直径是圆中最长的弦
2.下列条件中,能画唯一圆的是(B)
A.以已知点O为圆心
B.以点O为圆心,2
cm为半径
C.以1
cm为半径
D.经过已知点A,且半径为2
cm
3.已知⊙O的直径AB=6
cm,则圆上任意一点到圆心的距离等于(C)
A.2
cm
B.2.5
cm
C.3
cm
D.无法确定
4.如图,圆中有1条直径,3条弦,圆中以A为一个端点的优弧有4条,劣弧有4条.
5.如图,⊙O的半径是5,∠AOB=60°,则AB=5.
6.孙老师上数学课时忘记了带圆规,但他手里有一根小细绳,你能帮他在黑板上画一个圆吗?并说明理由.
解:能.将小细绳绕着它的一个端点,旋转一周,另一个端点走过的路线即为一个圆,理由:圆可以看成是到定点的距离等于定长的所有点组成的图形.
知识点2 点与圆的位置关系
7.(湘西中考)⊙O的半径为5
cm,点A到圆心O的距离OA=3
cm,则点A与⊙O的位置关系为(B)
A.点A在圆上
B.点A在圆内
C.点A在圆外
D.无法确定
8.已知⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是(A)
A.点P在⊙O内
B.点P的⊙O上
C.点P在⊙O外
D.点P在⊙O上或⊙O外
9.已知⊙O的半径为3
cm,⊙O所在的平面内一点P,当PO=3__cm时,点P在⊙O上;当PO<3__cm时,点P在⊙O内;当PO>3__cm时,点P在⊙O外.
10.在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,r=3为半径作圆,判断A,B两点和⊙C的位置关系.
解:∵∠C=90°,AC=4,AB=5,∴BC=3.
∵AC=4>r,∴点A在⊙C外.
∵BC=3=r,∴点B在⊙C上.
中档题
11.下列命题,其中正确的有(A)
①两个端点能够重合的弧是等弧;②面积相等的两个圆是等圆;③弦是圆上任意两点之间的部分;④同圆或等圆中,劣弧比优弧短.
A.1个
B.2个
C.3个
D.4个
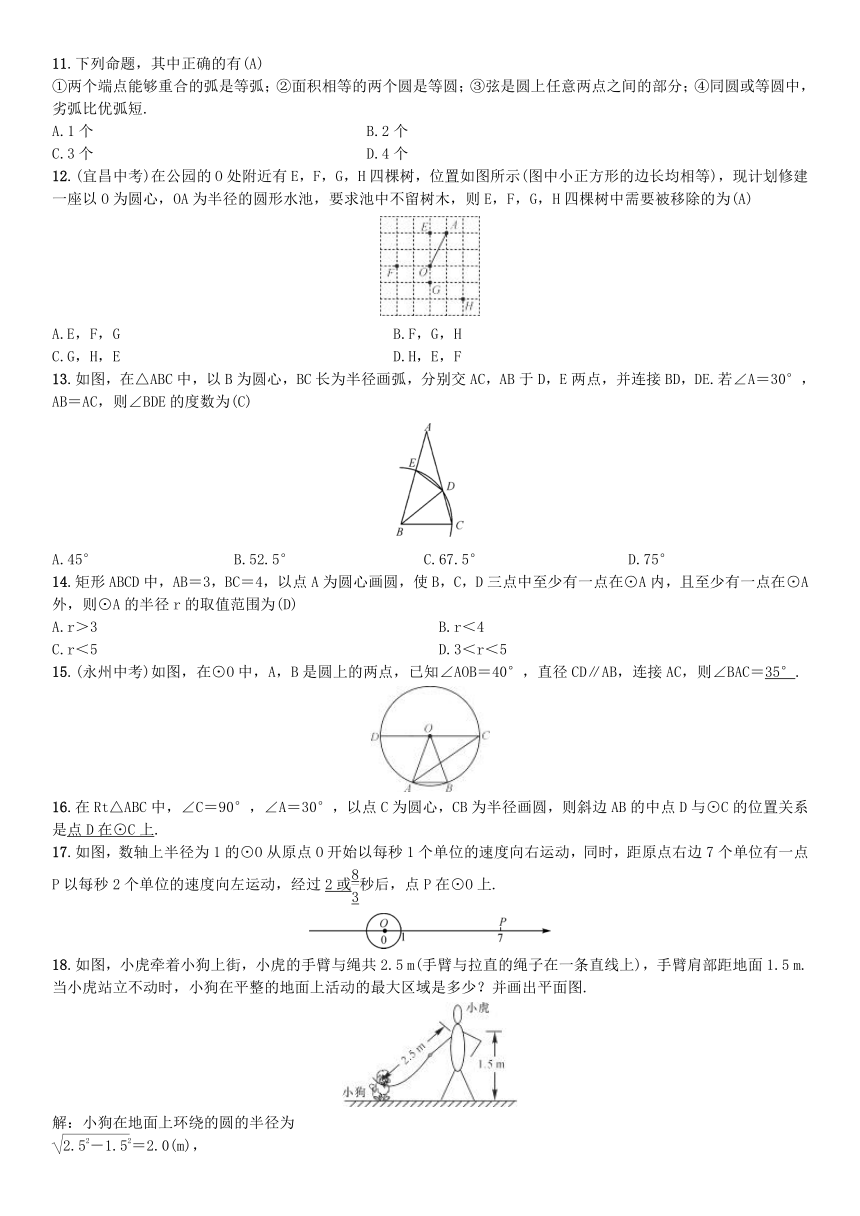
12.(宜昌中考)在公园的O处附近有E,F,G,H四棵树,位置如图所示(图中小正方形的边长均相等),现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E,F,G,H四棵树中需要被移除的为(A)
A.E,F,G
B.F,G,H
C.G,H,E
D.H,E,F
13.如图,在△ABC中,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E两点,并连接BD,DE.若∠A=30°,AB=AC,则∠BDE的度数为(C)
A.45°
B.52.5°
C.67.5°
D.75°
14.矩形ABCD中,AB=3,BC=4,以点A为圆心画圆,使B,C,D三点中至少有一点在⊙A内,且至少有一点在⊙A外,则⊙A的半径r的取值范围为(D)
A.r>3
B.r<4
C.r<5
D.3<r<5
15.(永州中考)如图,在⊙O中,A,B是圆上的两点,已知∠AOB=40°,直径CD∥AB,连接AC,则∠BAC=35°.
16.在Rt△ABC中,∠C=90°,∠A=30°,以点C为圆心,CB为半径画圆,则斜边AB的中点D与⊙C的位置关系是点D在⊙C上.
17.如图,数轴上半径为1的⊙O从原点O开始以每秒1个单位的速度向右运动,同时,距原点右边7个单位有一点P以每秒2个单位的速度向左运动,经过2或秒后,点P在⊙O上.
18.如图,小虎牵着小狗上街,小虎的手臂与绳共2.5
m(手臂与拉直的绳子在一条直线上),手臂肩部距地面1.5
m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
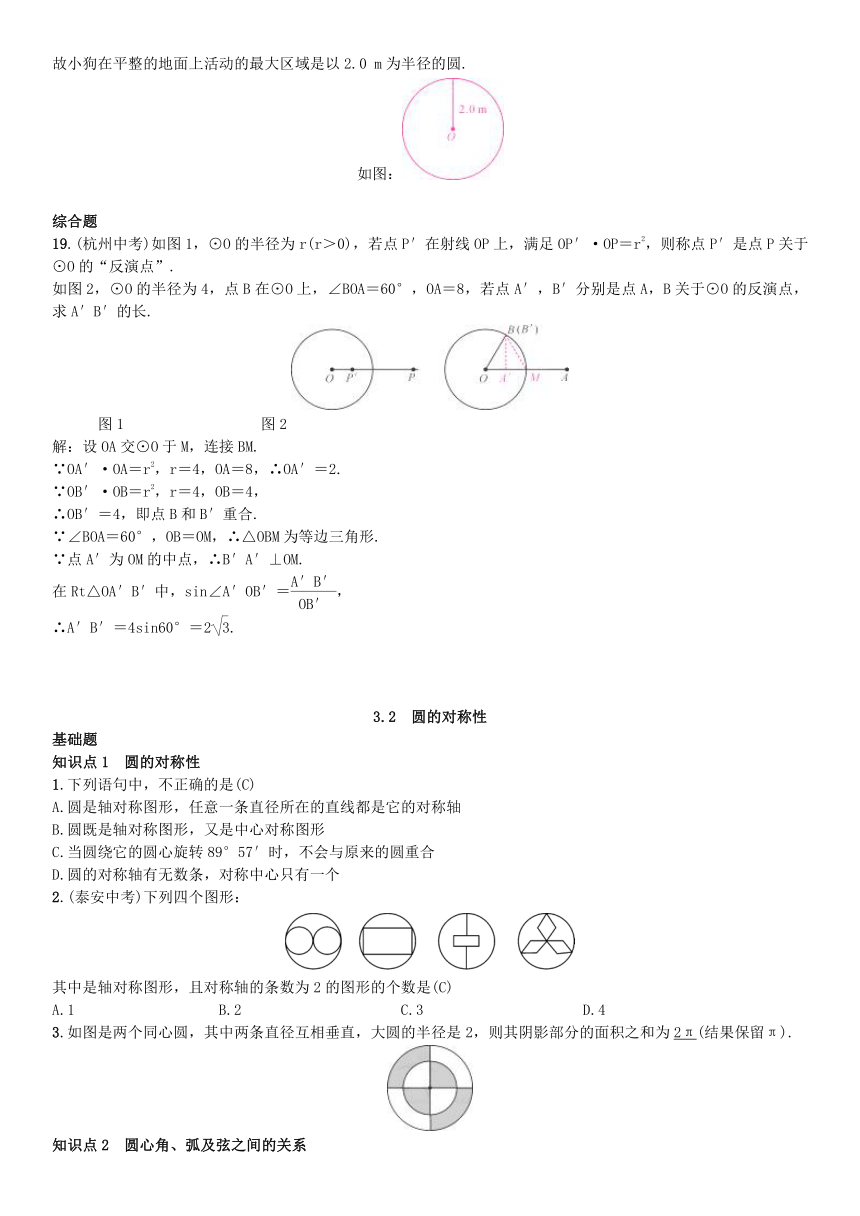
解:小狗在地面上环绕的圆的半径为
=2.0(m),
故小狗在平整的地面上活动的最大区域是以2.0
m为半径的圆.
如图:
综合题
19.(杭州中考)如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′·OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
图1 图2
解:设OA交⊙O于M,连接BM.
∵OA′·OA=r2,r=4,OA=8,∴OA′=2.
∵OB′·OB=r2,r=4,OB=4,
∴OB′=4,即点B和B′重合.
∵∠BOA=60°,OB=OM,∴△OBM为等边三角形.
∵点A′为OM的中点,∴B′A′⊥OM.
在Rt△OA′B′中,sin∠A′OB′=,
∴A′B′=4sin60°=2.
3.2 圆的对称性
基础题
知识点1 圆的对称性
1.下列语句中,不正确的是(C)
A.圆是轴对称图形,任意一条直径所在的直线都是它的对称轴
B.圆既是轴对称图形,又是中心对称图形
C.当圆绕它的圆心旋转89°57′时,不会与原来的圆重合
D.圆的对称轴有无数条,对称中心只有一个
2.(泰安中考)下列四个图形:
其中是轴对称图形,且对称轴的条数为2的图形的个数是(C)
A.1
B.2
C.3
D.4
3.如图是两个同心圆,其中两条直径互相垂直,大圆的半径是2,则其阴影部分的面积之和为2π(结果保留π).
知识点2 圆心角、弧及弦之间的关系
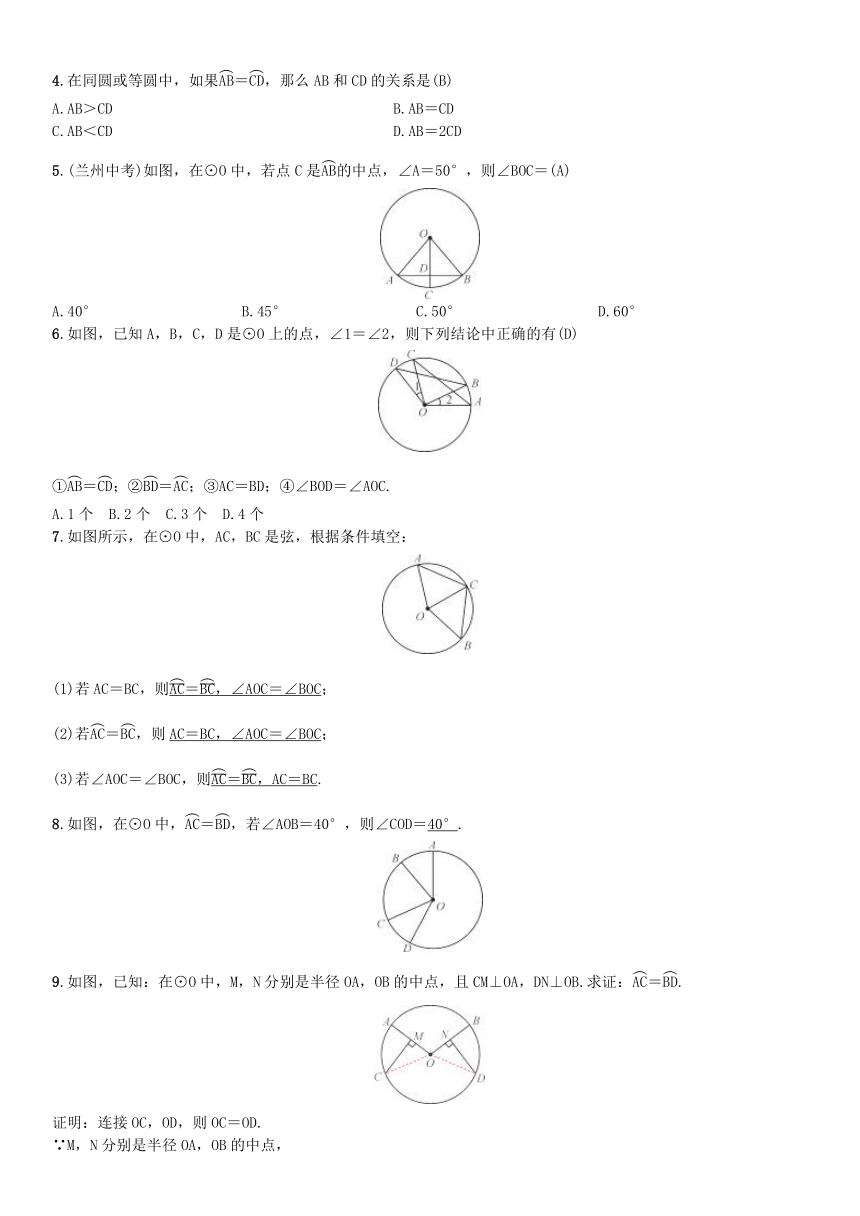
4.在同圆或等圆中,如果=,那么AB和CD的关系是(B)
A.AB>CD
B.AB=CD
C.AB<CD
D.AB=2CD
5.(兰州中考)如图,在⊙O中,若点C是的中点,∠A=50°,则∠BOC=(A)
A.40°
B.45°
C.50°
D.60°
6.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,则下列结论中正确的有(D)
①=;②=;③AC=BD;④∠BOD=∠AOC.
A.1个
B.2个
C.3个
D.4个
7.如图所示,在⊙O中,AC,BC是弦,根据条件填空:
(1)若AC=BC,则=,∠AOC=∠BOC;
(2)若=,则AC=BC,∠AOC=∠BOC;
(3)若∠AOC=∠BOC,则=,AC=BC.
8.如图,在⊙O中,=,若∠AOB=40°,则∠COD=40°.
9.如图,已知:在⊙O中,M,N分别是半径OA,OB的中点,且CM⊥OA,DN⊥OB.求证:=.
证明:连接OC,OD,则OC=OD.
∵M,N分别是半径OA,OB的中点,
∴OM=ON.
∵CM⊥OA,DN⊥OB,
∴∠OMC=∠OND=90°.
在Rt△OMC和Rt△OND中,
∴Rt△OMC≌Rt△OND(HL).
∴∠MOC=∠NOD.∴=.
中档题
10.下列说法:①等弧对等弦;②等弦对等弧;③等弦所对的圆心角相等;④相等的圆心角所对的弧相等;⑤等弧所对的圆心角相等.其中正确的个数为(B)
A.1
B.2
C.3
D.4
11.形如半圆形的量角器直径为4
cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的两个端点P、Q,线段PQ交y轴于点A,则点A的坐标为(B)
A.(-1,)
B.(0,)
C.(,0)
D.(1,)
12.如图,扇形OAB的圆心角为90°,点C,D是的三等分点,半径OC,OD分别与弦AB交于点E,F,下列说法错误的是(A)
A.AE=EF=FB
B.AC=CD=DB
C.EC=FD
D.∠DFB=75°
13.如图,在⊙O中,=2,则下列结论正确的是(C)
A.AB>2CD
B.AB=2CD
C.AB<2CD
D.以上都不正确
14.如图,已知AB是⊙O的直径,C,D,E,F,G是上的点,且有=====,则∠OCG=30°.
15.(黄石中考)如图,A,B是⊙O上的两点,∠AOB=120°,C是的中点.
(1)求证:AB平分∠OAC;
(2)延长OA至P使得AP=OA,连接PC,若⊙O的半径R=1,求PC的长.
解:(1)证明:连接OC.
∵∠AOB=120°,C是的中点,
∴∠AOC=∠BOC=60°.
又∵OA=OC=OB,
∴△AOC、△BOC是等边三角形.
∴OA=OB=BC=AC.
∴四边形AOBC是菱形.
∴AB平分∠OAC.
(2)∵OA=AP,OA=AC,∴AP=AC.
又∵∠CAO=∠ACO=60°,
∴∠APC=30°,∠OCP=90°.
∴PC=OC=.
综合题
16.我们学习了“弧、弦、圆心角的关系”,实际上我们还可以得到“圆心角、弧、弦、弦心距之间的关系”如下:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们对应的其余各组量也相等[弦心距指从圆心到弦的距离(如图1中的OC、OC′),弦心距也可以说成圆心到弦的垂线段的长度].请直接运用圆心角、弧、弦、弦心距之间的关系解答下列问题:
如图2,O是∠EPF的平分线上一点,以点O为圆心的圆与角的两边分别交于点A,B,C,D.
(1)求证:AB=CD;
(2)若角的顶点P在圆上,上述结论还成立吗?若不成立,请说明理由;若成立,请加以证明.
解:(1)证明:过O作OM⊥AB于M,ON⊥CD于N,则∠OMB=∠OND=90°.
∵PO平分∠EPF,∴OM=ON.
∵OM,ON分别是弦AB,CD的弦心距,
∴AB=CD.
(2)上述结论成立.
证明:当点P在⊙O上时,由(1)知OM=ON,
∵OM,ON分别是弦AB,CD的弦心距,
∴PB=PD,即AB=CD.
3.3 垂径定理
基础题
知识点1 垂径定理
1.(黄石中考)如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=(A)
A.5
B.7
C.9
D.11
2.如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16
cm,OC=6
cm,则⊙O的半径为(B)
A.
cm
B.10
cm
C.8
cm
D.
cm
3.(三明中考)如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是(A)
A.2
B.3
C.4
D.5
4.(黑龙江中考)如图,⊙O的直径CD=10
cm,AB是⊙O的弦,且AB⊥CD,垂足为P,AB=8
cm,则sin∠OAP的值是(C)
A.
B.
C.
D.
5.(广元中考)如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是(B)
A.CE=DE
B.AE=OE
C.=
D.△OCE≌△ODE
知识点2 垂径定理的推论
6.下列说法错误的是(C)
A.垂直于弦的直径平分弦
B.垂直于弦的直径平分弦所对的弧
C.平分弦的直径平分弦所对的弧
D.平分弧的直径垂直平分弧所对的弦
7.如图,AB是⊙O的弦,OC为半径,与AB交于点D,且AD=BD,已知AB=6
cm,OD=4
cm,则DC的长为(D)
A.5
cm
B.2.5
cm
C.2
cm
D.1
cm
知识点3 垂径定理的应用
8.如图是一个圆弧形门拱,拱高AB=1
m,跨度CD=4
m,那么这个门拱的半径为(B)
A.2
m
B.2.5
m
C.3
m
D.5
m
9.(东营中考)如图,水平放置的圆柱形排水管道的截面直径是1
m,其中水面的宽AB为0.8
m,则排水管内水的深度为0.8m.
10.如图所示,某窗户由矩形和弓形组成,已知弓形的跨度AB=3
m,弓形的高EF=1
m,现计划安装玻璃,请帮工程师求出所在⊙O的半径r.
解:∵弓形的跨度AB=3
m,EF为弓形的高,
∴OE⊥AB.
∴AF=AB=
m.
∵所在⊙O的半径为r,弓形的高EF=1
m,
∴AO=r,OF=r-1.
在Rt△AOF中,AO2=AF2+OF2,
即r2=()2+(r-1)2.解得r=.
故r=
m.
中档题
11.如图,⊙O的弦AB,AC的夹角为50°,M,N分别为和的中点,OM,ON分别交AB,AC于E,F,则∠MON的度数为(C)
A.110°
B.120°
C.130°
D.100°
12.如图,小明家凉台呈圆弧形,凉台的宽度AB为8
m,凉台的最外端C点离AB的距离CD为2
m,则凉台所在圆的半径为(B)
A.4
m
B.5
m
C.6
m
D.7
m
13.如图,将半径为2
cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为(C)
A.2
cm
B.
cm
C.2
cm
D.2
cm
14.CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=8,则BE的长是(C)
A.8
B.2
C.2或8
D.3或7
15.(黔西南中考)如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,若CD=6,BE=1,则⊙O的直径为10.
16.(绍兴中考)如图1,小敏利用课余时间制作了一个脸盆架,图2是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40
cm,脸盆的最低点C到AB的距离为10
cm,则该脸盆的半径为25cm.
图1
图2
17.(湖州中考)已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.
解:(1)证明:作OE⊥AB,垂足为E,
则AE=BE,CE=DE,
∴AE-CE=BE-DE,
即AC=BD.
(2)由(1)可知,OE⊥AB,OE⊥CD,
连接OC,OA.
∵OE=6,
∴CE===2,
AE===8.
∴AC=AE-CE=8-2.
综合题
18.如图,某地有一座圆弧形拱桥,桥下水面宽度AB为7.2
m,拱高CD为2.4
m.
(1)求拱桥的半径;
(2)现有一艘宽3
m,船舱顶部为长方形并高出水面2
m的货船要经过这里,问此货船能顺利通过拱桥吗?
解:(1)连接OB.
∵OC⊥AB,
∴D为AB的中点.
∵AB=7.2
m,
∴BD=AB=3.6
m.
设OB=OC=r,则OD=(r-2.4)m.
在Rt△BOD中,根据勾股定理,得
r2=(r-2.4)2+3.62,解得r=3.9.
∴拱桥的半径为3.9
m.
(2)令船舱顶部两点分别分M,N(CN在M的右边),连接ON.
∵CD=2.4
m,船舱顶部为长方形并高出水面2
m,∴CE=2.4-2=0.4(m).
∴OE=r-CE=3.9-0.4=3.5(m).
在Rt△OEN中,EN2=ON2-OE2=3.92-3.52=2.96(m2),
∴EN=(m),
MN=2EN=2×≈3.44
m>3
m.
∴此货船能顺利通过这座拱桥.
3.4 圆周角和圆心角的关系
第1课时 圆周角定理及其推论1
基础题
知识点1 圆周角的概念
1.(柳州中考)下列四个图中,∠x是圆周角的是(C)
A B
C
D
2.如图,图中的圆周角有(C)
A.10个
B.11个
C.12个
D.13个
知识点2 圆周角定理
3.(温州中考)如图,已知A,B,C在⊙O上,为优弧,下列选项中与∠AOB相等的是(A)
A.2∠C
B.4∠B
C.4∠A
D.∠B+∠C
4.(济宁中考)如图,在⊙O中,=,∠AOB=40°,则∠ADC的度数是(C)
A.40°
B.30°
C.20°
D.15°
5.如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是(A)
A.25°
B.30°
C.40°
D.50°
6.(娄底中考)如图,将直角三角板60°角的顶点放在圆心O上,斜边和一直角边分别与⊙O相交于A,B两点,P是优弧AB上任意一点(与A,B不重合),则∠APB=30度.
知识点3 圆周角定理的推论1
7.(自贡中考)如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是(C)
A.15°
B.25°
C.30°
D.75°
8.(百色中考)如图,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=65°.
9.如图,已知A,B,C,D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD,AD.求证:DB平分∠ADC.
证明:∵AB=BC,
∴=.
∴∠ADB=∠BDC.
∴DB平分∠ADC.
中档题
10.(巴彦淖尔中考)如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=40°,则∠ABD与∠AOD分别等于(B)
A.40°,80°
B.50°,100°
C.50°,80°
D.40°,100°
11.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为(B)
A.15°
B.28°
C.29°
D.34°
12.(泰安中考)如图,点A,B,C是⊙O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于(B)
A.12.5°
B.15°
C.20°
D.22.5°
13.如图,△ABC内接于⊙O,若∠OAB=28°,则∠C的大小为62°.
14.(临夏中考)如图,在⊙O中,弦AC=2,点B是圆上一点,且∠ABC=45°,则⊙O的半径R=.
15.如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=6,求tan∠DEB的值.
解:(1)连接OB,
∵OD⊥AB,∴=.
∴∠BOD=∠AOD=52°.
∴∠DEB=∠BOD=26°.
(2)∵OD⊥AB,OC=3,OA=6,
∴OC=OA,即∠OAC=30°.
∴∠AOC=60°.
∴∠DEB=∠AOC=30°.
∴tan∠DEB=.
16.如图,在⊙O中,AB=AC,∠CBD=30°,∠BCD=20°,试求∠BAC的度数.
解:连接OB,OC,OD.
∵∠BOD=2∠BCD,∠COD=2∠CBD,∠CBD=30°,
∠BCD=20°,
∴∠COD=60°,∠BOD=40°.
∴∠BOC=100°,
∠BAC=∠BOC=50°.
综合题
17.(台州中考)如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
解:(1)∵BC=DC,
∴=.
∴∠BAC=∠CAD=∠CBD.
∵∠CBD=39°,
∴∠BAC=∠CAD=39°.
∴∠BAD=∠BAC+∠DAC=78°.
(2)证明:∵EC=BC,
∴∠CBE=∠CEB.
∵∠CBE=∠1+∠CBD,∠CEB=∠2+∠BAC,
∴∠1+∠CBD=∠2+∠BAC.
又∵∠BAC=∠CBD,∴∠1=∠2.
第2课时 圆周角定理的推论2、3
基础题
知识点1 圆周角定理的推论2
1.(湖州中考)如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是(C)
A.35°
B.45°
C.55°
D.65°
2.(台州中考)从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是(B)
3.(玉林中考)如图,CD是⊙O的直径,已知∠1=30°,则∠2=(C)
A.30°
B.45°
C.60°
D.70°
4.(常州中考)如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M,N,量得OM=8
cm,ON=6
cm,则该圆玻璃镜的半径是(B)
A.
cm
B.5
cm
C.6
cm
D.10
cm
5.(眉山中考)如图,A,D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC=(B)
A.64°
B.58°
C.72°
D.55°
6.如图,在半径为5
cm的⊙O中,AB为直径,∠ACD=30°,求弦BD的长.
解:∵AB为直径,
∴∠ADB=90°.
又∵∠ABD=∠ACD=30°,
∴BD=AB·cos∠ABD=10×=5(cm).
知识点2 圆周角定理的推论3
7.(杭州中考)圆内接四边形ABCD中,已知∠A=70°,则∠C=(D)
A.20°
B.30°
C.70°
D.110°
8.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是(B)
A.115°
B.105°
C.100°
D.95°
9.(常德中考)如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为(D)
A.50°
B.80°
C.100°
D.130°
10.在圆内接四边形ABCD中,若∠A∶∠B∶∠C=1∶2∶5,则∠B的度数是(C)
A.30°
B.45°
C.60°
D.120°
11.(来宾中考)如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=110°,则∠α=140°.
中档题
12.(达州中考)如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为(C)
A.
B.2
C.
D.
13.(烟台中考)如图,Rt△ABC的斜边AB与量角器的直径恰好重合,B点与0刻度线的一端重合,∠ABC=40°,射线CD绕点C转动,与量角器外沿交于点D,若射线CD将△ABC分割出以BC为边的等腰三角形,则点D在量角器上对应的度数是(D)
A.40°
B.70°
C.70°或80°
D.80°或140°
14.(无锡中考)如图,AB是半圆O的直径,C,D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
解:(1)∵OD∥BC,
∴∠DOA=∠B=70°
又∵OA=OD,
∴∠DAO=∠D=55°.
∵AB是直径,∴∠C=90°.∴∠CAB=20°.
∴∠CAD=35°.
(2)∵∠C=90°,AB=4,AC=3,∴BC=.
∵O是AB中点,OD∥BC,∴OE==.
∴DE=2-.
15.(温州中考)如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1=∠F;
(2)若sinB=,EF=2,求CD的长.
解:(1)证明:连接DE,
∵BD是⊙O的直径,
∴∠DEB=90°.
∵E是AB的中点,
∴DA=DB.
∴∠1=∠B.
∵∠B=∠F,∴∠1=∠F.
(2)∵∠1=∠F,
∴AE=EF=2.
∴AB=2AE=4.
在Rt△ABC中,AC=AB·sinB=4,
∴BC==8.
设CD=x,则AD=BD=8-x.
∵AC2+CD2=AD2,即42+x2=(8-x)2,
∴x=3,即CD=3.
综合题
16.(1)如图1,PA,PB是⊙O的两条弦,AB为直径,C为的中点,弦CD⊥PA于点E,写出AB与AC的数量关系,并证明;
(2)如图2,PA,PB是⊙O的两条弦,AB为弦,C为劣弧的中点,弦CD⊥PA于E,写出AE,PE与PB的数量关系,并证明.
解:(1)AB=AC.
证明:∵AB为直径,C为的中点,
∴∠ACB=90°,AC=BC.
∴AB=AC.
(2)AE=PB+PE.
证明:在AE上截取AF=BP,连接AC,BC,FC,PC.
∵C为劣弧的中点,即=,
∴AC=BC.
在△CAF和△CBP中,
,
∴△CAF≌△CBP.
∴CF=CP.
又∵CD⊥PA,
∴EF=EP.
∴AE=AF+EF=PB+PE.
小专题(八) 与圆的基本性质有关的计算与证明
1.如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.
(1)求∠B的大小;
(2)已知圆心O到BD的距离为3,求AD的长.
解:(1)∵∠CAB=∠CDB,∠CAB=40°,∴∠CDB=40°.
又∵∠APD=65°,
∴∠B=∠APD-∠CDB=25°.
(2)过点O作OE⊥BD于点E,则OE=3,BE=DE.
又∵O是AB的中点,
∴OE是△ABD的中位线.
∴AD=2OE=6.
2.(南京中考)A,B是⊙O上的两个定点,P是⊙O上的动点(P不与A,B重合),我们称∠APB是⊙O上关于点A,B的滑动角.已知∠APB是⊙O上关于点A,B的滑动角.
(1)若AB是⊙O的直径,则∠APB=90°;
(2)如图,若⊙O的半径是1,AB=,求∠APB的度数.
解:连接OA,OB,AB.
∵OA=OB=1,AB=,
∴OA2+OB2=AB2.
∴∠AOB=90°.
∴∠APB=∠AOB=45°.
3.如图,AB是⊙O的直径,C,D两点在⊙O上,若∠C=45°.
(1)求∠ABD的度数;
(2)若∠CDB=30°,BC=3,求⊙O的半径.
解:(1)∵∠C=45°,
∴∠A=∠C=45°.
∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠ABD=45°.
(2)连接AC.
∵AB是⊙O的直径,
∴∠ACB=90°.
∵∠CAB=∠CDB=30°,BC=3,
∴AB=6.
∴⊙O的半径为3.
4.(宁夏中考)如图,已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2,求CD的长.
解:(1)证明:∵ED=EC,
∴∠EDC=∠C.
∵∠EDC=∠B,∴∠B=∠C.∴AB=AC.
(2)连接AE.
∵AB为直径,∴AE⊥BC.
由(1)知AB=AC,∴BE=CE=BC=.
∵∠C=∠C,∠EDC=∠B,∴△CDE∽△CBA.
∴=.∴CE·CB=CD·AC.
∵AC=AB=4,∴×2=4CD.
∴CD=.
5.(深圳中考)如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧形小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
解:∵=,DE=8,
解得EF=12.
∵EG=3,HF=1,
∴GH=EF-EG-HF=8.
由垂径定理,得GM=GH=4.
又MN=2,设半径OG=R,则OM=R-2.
在Rt△OMG中,由勾股定理,得
OM2+MG2=OG2.
∴(R-2)2+42=R2.解得R=5.
答:小桥所在圆的半径为5米.
6.(安徽中考)在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
解:(1)连接OQ.
∵PQ∥AB,PQ⊥OP,
∴OP⊥AB.
∵AB=6,∴OB=3.
∵∠ABC=30°,
tan∠ABC=,即=.
∴OP=.
由勾股定理,得
PQ===.
(2)连接OQ.
由勾股定理,得PQ==.
要使PQ取最大值,需OP取最小值,此时OP⊥BC.
∵∠ABC=30°,
∴OP=OB=,此时PQ最大==.
7.(烟台中考)如图,以△ABC的一边AB为直径的半圆与其他两边AC,BC的交点分别为D,E,且=.
(1)试判断△ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求sin∠ABD的值.
解:(1)△ABC为等腰三角形.理由如下:
连接AE,∵=,
∴∠DAE=∠BAE,
即AE平分∠BAC.
∵AB为直径,
∴∠AEB=∠AEC=90°,即AE⊥BC.
又∵AE=AE,
∴△CAE≌△BAE.∴AC=AB.
∴△ABC为等腰三角形.
(2)∵△ABC为等腰三角形,AE⊥BC,
∴BE=CE=BC=×12=6.
在Rt△ABE中,∵AB=10,BE=6,
∴AE==8.
∵AB为直径,∴∠ADB=90°.
∴S△ABC=AE·BC=BD·AC.
∴BD==.
在Rt△ABD中,∵AB=10,BD=,
∴AD==.
∴sin∠ABD===.
8.如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D为BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED,若存在,请求出PB的长;若不存在,请说明理由.
解:(1)证明:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°.
∵点D是BC的中点,
∴AD是线段BC的垂直平分线.
∴AB=AC.
∵AB=BC,∴AB=BC=AC.
∴△ABC为等边三角形.
(2)连接BE.
∵AB是直径,∴∠AEB=90°.
∴BE⊥AC.
∵△ABC是等边三角形,
∴AE=EC,即E为AC的中点.
∵D是BC的中点,故DE为△ABC的中位线,
∴BD=BC=1,DE=AB=×2=1.
(3)假设存在点P,使△PBD≌△AED.
∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°.
∴∠PBD=120°.
∵DE∥AB,∴∠AED=120°.
又∵△PBD≌△AED,BD=ED,
∴PB=AE=1.
周周练(3.1~3.4)
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.下列说法中,错误的是(B)
A.直径相等的两个圆是等圆
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.圆中最长的弦是直径
D.一条弦把圆分成两条弧,这两条弧可能是等弧
2.(娄底中考)如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为(C)
A.20°
B.40°
C.50°
D.70°
3.(泰安中考)如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于(D)
A.180°-2α
B.2α
C.90°+α
D.90°-α
4.如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是(B)
A.3≤OM≤5
B.4≤OM≤5
C.3<OM<5
D.4<OM<5
5.AB是⊙O的弦,OQ⊥AB,垂足为Q,再以OQ为半径作同心圆,称作小⊙O,点P是AB上异于A,B,Q的任意一点,则点P位置是(D)
A.在大⊙O上
B.在大⊙O外部
C.在小⊙O内部
D.在小⊙O外,大⊙O内
6.如图,△ABC内接于⊙O,∠C=30°,AB=2,则⊙O的半径为(B)
A.
B.2
C.2
D.4
7.已知⊙O的直径CD=10
cm,AB是⊙O的弦,AB=8
cm,且AB⊥CD,垂足为M,则AC的长为(C)
A.2
cm
B.4
cm
C.2
cm或4
cm
D.2
cm或4
cm
8.(泰安中考)如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE∶S△CDB的值等于(D)
A.1∶
B.1∶
C.1∶2
D.2∶3
二、填空题(每小题5分,共20分)
9.已知⊙O的直径为6,点M到圆心O的距离为4,则点M与⊙O的位置关系是点M在⊙O外.
10.如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于60度.
11.如图,AD和AC分别是⊙O的直径和弦,且∠CAD=30°,OB⊥AD,交AC于点B,若OB=3,则BC=3.
12.如图,点A,B,C,D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=60°.
三、解答题(共48分)
13.(10分)已知⊙O的半径为1,点P与圆心O的距离为d,且方程x2-2x+d=0有实数根,则点P与⊙O有怎样的位置关系?
解:∵方程x2-2x+d=0有实数根,
∴(-2)2-4×1×d=4-4d≥0.∴d≤1.
又∵d≥0,∴0≤d≤1.
∴当d=1时,点P在⊙O上;
当0≤d<1时,点P在⊙O内.
综上所述,点P在⊙O内或⊙O上.
14.(12分)如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一点(不与点A,B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)弦长AB等于2(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数.
解:连接OA.
∵OA=OB,OA=OD,
∴∠BAO=∠B,∠DAO=∠D.
∴∠DAB=∠BAO+∠DAO=∠B+∠D.
又∵∠B=30°,∠D=20°,
∴∠DAB=50°.
∴∠BOD=2∠DAB=100°.
15.(12分)已知⊙O的直径为10,点A,B,C在⊙O上,∠CAB的平分线交⊙O于点D.
图1 图2
(1)如图1,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图2,若∠CAB=60°,求BD的长.
解:(1)∵BC是⊙O的直径,
∴∠CAB=∠BDC=90°.
∵在Rt△CAB中,BC=10,AB=6,
∴AC===8.
∵AD平分∠CAB,∴=.∴CD=BD.
在Rt△BDC中,BC=10,CD2+BD2=BC2,
∴BD=CD=5.
(2)连接OB,OD.
∵AD平分∠CAB,且∠CAB=60°,
∴∠DAB=∠CAB=30°.
∴∠DOB=2∠DAB=60°.
又∵OB=OD,∴△OBD是等边三角形.
∴BD=OB=×10=5.
16.(14分)如图1所示,已知△ABC是等边三角形,以BC为直径作⊙O交AB,AC于D,E.
(1)求证:△ODE是等边三角形;
(2)如图2所示,若∠A=60°,AB≠AC,则(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
解:(1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°.
∵OB=OC=OD=OE,
∴△BOD,△COE是等边三角形.
∴∠BOD=∠COE=60°.∴∠DOE=60°.
∴△ODE是等边三角形.
(2)仍然成立.
证明:连接CD.
∵BC是⊙O的直径,
∴∠BDC=90°.∴∠ADC=90°.
∵∠A=60°,∴∠ACD=30°.
∴∠DOE=2∠ACD=60°.
∵OD=OE,
∴△ODE是等边三角形.
3.5 确定圆的条件
基础题
知识点1 确定圆的条件
1.下列条件,可以画出唯一一个圆的是(D)
A.已知圆心
B.已知半径
C.已知直径
D.已知不在同一条直线上的三个点
2.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是(B)
A.点P
B.点Q
C.点R
D.点M
3.在同一平面上有A,B,C三点,若经过A,B,C这三点画圆,则可画(C)
A.0个
B.1个
C.0个或1个
D.无数个
4.平面上有三个点A,B,C,若AB=5
cm,BC=3
cm,CA=4
cm,则过A,B,C三点可以(填“可以”或“不可以”)确定一个圆,且圆心在AB上,是AB的中点.
知识点2 三角形的外接圆
5.(株洲中考)如图,⊙O是△ABC的外接圆,∠A=68°,则∠OBC的大小是(A)
A.22°
B.26°
C.32°
D.68°
6.一个三角形的外心在其内部,则这个三角形是(C)
A.任意三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
7.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则以A,B,C为顶点的三角形外接圆的圆心坐标是(C)
A.(2,3)
B.(3,2)
C.(3,1)
D.(1,3)
8.点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为(C)
A.40°
B.100°
C.40°或140°
D.40°或100°
9.(扬州中考)如图,⊙O是△ABC的外接圆,直径AD=4,∠ABC=∠DAC,则AC的长为2.
10.如图,一只猫观察到一老鼠洞的三个洞口A,B,C,这三个洞口不在同一条直线上,请问这只猫应该在什么地方才能最省力同时顾及三个洞口?作出这个位置.
解:如图,连接AB,BC,分别作线段AB,BC的垂直平分线,且相交于点O,点O即为所求.
中档题
11.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是(B)
A.第①块
B.第②块
C.第③块
D.第④块
12.小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹);
(2)若△ABC中,AB=8米,AC=6米,∠BAC=90°,试求小明家圆形花坛的面积.
解:(1)用尺规作出AB,AC的垂直平分线,交于O点,以O为圆心,OA长为半径作出⊙O,⊙O即为花坛的位置,如图.
(2)∵∠BAC=90°,AB=8米,AC=6米,
∴BC=10米.
∴△ABC外接圆的半径为5米.
∴小明家圆形花坛的面积为25π平方米.
13.如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.
(1)当α=35°时,求β的度数;
(2)猜想α与β之间的关系,并给予证明.
解:(1)连接OB,则OA=OB.
∵∠OAB=35°,
∴∠OBA=∠OAB=35°.
∴∠AOB=180°-35°-35°=110°.
∴β=∠C=∠AOB=55°.
(2)α与β之间的关系是α+β=90°.
证明:∵∠OBA=∠OAB=α,
∴∠AOB=180°-2α.
∵β=∠C=∠AOB,
∴β=(180°-2α)=90°-α.
∴α+β=90°.
综合题
14.(福州中考)如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
(1)求BC的长;
(2)求⊙O的半径.
解:(1)作AE⊥BC,垂足为E.
在Rt△ABE中,
∵∠B=45°,AB=3,
∴AE=BE=3.
在Rt△ACE中,∵∠ACE=60°,AE=3,
∴CE===.
∴BC=BE+CE=3+.
(2)作直径AF,连接CF,则∠ACF=90°.
在Rt△ACE中,∵∠ACE=60°,AE=3,
∴AC===2.
∵∠F=∠D,∠D=∠ACB=60°,
∴∠F=60°.
在Rt△AFC中,∵sinF=,
∴AF===4.
∴⊙O半径OA=2.
3.6 直线和圆的位置关系
第1课时 直线和圆的位置关系及切线的性质
基础题
知识点1 直线和圆的位置关系
1.下图中直线l是⊙O的切线的图形是(C)
2.(梧州中考)已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为(C)
A.相离
B.相切
C.相交
D.无法确定
3.已知⊙O的面积为9π
cm2,若点O到直线l的距离为π
cm,则直线l与⊙O的位置关系是(C)
A.相交
B.相切
C.相离
D.无法确定
4.在平面直角坐标系xOy中,以点(-3,4)为圆心,4为半径的圆(C)
A.与x轴相交,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
5.已知⊙O的直径为6,圆心O到直线l的距离为d,(1)当直线l与⊙O相离时,d的取值范围是d>3;(2)当直线l与⊙O相切时,则d=3;
(3)当直线l与⊙O相交时,d的取值范围是d<3.
6.(湘西中考改编)如图,在Rt△ABC中,∠C=90°,BC=3
cm,AC=4
cm,以点C为圆心,以2.5
cm为半径画圆,则⊙C与直线AB有何种位置关系?请说明理由.
解:⊙O与直线AB相交.理由:
过C作CD⊥AB于D.
∵在Rt△ABC中,∠C=90°,BC=3
cm,AC=4
cm,
∴AB==5
cm.
∵S△ABC=AC·BC=AB·CD,
∴3×4=5CD.∴CD=2.4<2.5,即d<r.
∴⊙C与直线AB的位置关系是相交.
知识点2 切线的性质
7.如图,PA,PB是⊙O的切线,切点分别是A,B,如果∠P=60°,那么∠AOB等于(C)
A.60°
B.90°
C.120°
D.150°
8.(海南中考)如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.∠APO=40°,则∠ABC的度数为(B)
A.20°
B.25°
C.40°
D.50°
9.(赤峰中考)如图,两同心圆的大圆半径长为5
cm,小圆半径长为3
cm,大圆的弦AB与小圆相切,切点为C,则弦AB的长是8__cm.
10.(丽水中考改编)如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.求证:∠A=∠ADE.
证明:连接OD.
∵DE是切线,∴∠ODE=90°.
∴∠ADE+∠BDO=90°.
∵∠ACB=90°,
∴∠A+∠B=90°.
∵OD=OB,∴∠B=∠BDO.
∴∠A=∠ADE.
中档题
11.(湖州中考)如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作⊙O的切线,交AB的延长线于点D,则∠D的度数是(B)
A.25°
B.40°
C.50°
D.65°
12.(益阳中考)如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为(B)
A.1
B.1或5
C.3
D.5
13.(永州中考)如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m=1;
(2)当m=2时,d的取值范围是1<d<3.
14.(龙岩中考)如图,Rt△ABC中,∠C=90°,BC=3,点O在AB上,OB=2,以OB长为半径的⊙O与AC相切于点D,交BC于点F,OE⊥BC于点E,则弦BF的长为2.
15.(丹东中考)如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
解:(1)证明:连接OD.
∵CD是⊙O切线,
∴∠ODC=90°,
即∠ODB+∠BDC=90°.
∵AB为⊙O的直径,
∴∠ADB=90°,即∠ODB+∠ADO=90°.
∴∠BDC=∠ADO.
∵OA=OD,∴∠ADO=∠A.∴∠BDC=∠A.
(2)∵CE⊥AE,∴∠E=∠ADB=90°.∴DB∥EC.∴∠DCE=∠BDC.
∵∠BDC=∠A,∴∠A=∠DCE.
又∵∠E=∠E,∴△AEC∽△CED.
∴=,即EC2=DE·AE.
∴16=2(2+AD).∴AD=6.
综合题
16.(金华中考)如图,已知AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F,连接OC,AC.
(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数;
②若⊙O的半径为2,求线段EF的长.
解:(1)证明:∵CD是⊙O的切线,∴OC⊥CD.
∵AD⊥CD,∴AD∥OC.∴∠DAC=∠OCA.
∵OC=OA,
∴∠OCA=∠OAC.
∴∠OAC=∠DAC.∴AC平分∠DAO.
(2)①∵AD∥OC,∴∠EOC=∠DAO=105°.
∵∠E=30°,∴∠OCE=45°.
②作OG⊥CE于点G,则CG=FG.
∵OC=2,∠OCE=45°,∴CG=OG=2,FG=2.
在Rt△OGE中,∠E=30°,OG=2,∴GE=2.
∴EF=GE-FG=2-2.
第2课时 切线的判定与三角形的内切圆
基础题
知识点1 切线的判定
1.下列直线是圆的切线的是(B)
A.与圆有公共点的直线
B.圆心到直线的距离等于半径的直线
C.垂直于圆的半径的直线
D.过圆直径外端点的直线
2.如图,AB是⊙O的直径,下列条件中不能判定直线AT是⊙O的切线的是(D)
A.AB=4,AT=3,BT=5
B.∠B=45°,AB=AT
C.∠B=55°,∠TAC=55°
D.∠ATC=∠B
3.如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为∠ABC=90°或AB⊥BC.
4.如图,点A,B,D在⊙O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=40°,直线BC与⊙O的位置关系为相切.
5.(济宁中考改编)如图,已知⊙O的直径AB=12,弦AC=10,D是弧BC的中点,过点D作DE⊥AC,交AC的延长线于点E.求证:DE是⊙O的切线.
证明:连接OD.
∵D为弧BC的中点,
∴=.
∴∠BOD=∠BAE.
∴OD∥AE.
∵DE⊥AC,∴∠AED=90°.
∴∠ODE=90°.∴OD⊥DE.
∴DE为⊙O的切线.
知识点2 三角形的内切圆
6.有关三角形内心的说法正确的是(D)
A.内心是三边垂直平分线的交点
B.内心是三条中线的交点
C.内心到三个顶点的距离相等
D.内心到三边的距离相等
7.如图,在△ABC中,∠A=50°,内切圆I与边BC,CA,AB分别相切于点D,E,F,则∠EDF的度数为(C)
A.55°
B.60°
C.65°
D.70°
8.如图,在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆的半径是(B)
A.
B.1
C.2
D.
中档题
9.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是(C)
A.点(0,3)
B.点(2,3)
C.点(5,1)
D.点(6,1)
10.如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,OB长为半径作⊙O,要使射线BA与⊙O相切,应将射线绕点B按顺时针方向旋转(B)
A.40°或80°
B.50°或110°
C.50°或100°
D.60°或120°
11.(徐州中考)如图,⊙O是△ABC的内切圆,若∠ABC=70°,∠ACB=40°,则∠BOC=125°.
12.(南充中考)如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.
解:(1)证明:连接OD,CD.
∵AC为⊙O的直径,
∴△BCD是直角三角形.
∵E为BC的中点,
∴BE=CE=DE.∴∠CDE=∠DCE.
∵OD=OC,∴∠ODC=∠OCD.
∵∠ACB=90°,∴∠OCD+∠DCE=90°.
∴∠ODC+∠CDE=90°,即OD⊥DE.
∴DE是⊙O的切线.
(2)设⊙O的半径为r,∵∠ODF=90°,
∴OD2+DF2=OF2,即r2+42=(r+2)2.解得r=3.
∴⊙O的直径为6.
13.(呼伦贝尔中考)如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得
ED=EA.
(1)求证:ED是⊙O的切线;
(2)当OE=10时,求BC的长.
解:(1)证明:连接OD.∵AC⊥AB,
∴∠BAC=90°,
即∠OAE=90°.
在△AOE和△DOE中,
∴△AOE≌△DOE(SSS).
∴∠OAE=∠ODE=90°,即OD⊥ED.
又∵OD是⊙O的半径,∴ED是⊙O的切线.
(2)∵AB是直径.
∴∠ADB=90°,即AD⊥BC.
又∵由(1)知,△AOE≌△DOE,
∴∠AEO=∠DEO.
又∵AE=DE,∴OE⊥AD.
∴OE∥BC.∴△AOE∽△ABC.
∴==.
∴BC=2OE=20,即BC的长是20.
综合题
14.(常德中考)已知,如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长.
解:(1)证明:连接FO,
∵点O为AC的中点,点F为BC的中点,
∴OF∥AB.
∵AC为⊙O的直径,
∴CE⊥AE.
∵OF∥AB,∴OF⊥CE.
∴OF所在直线垂直平分CE.
∴FC=FE,OE=OC.
∴∠FEC=∠FCE,∠OEC=∠OCE.
∵∠ACB=90°,
∴∠OCE+∠FCE=90°.
∴∠OEC+∠FEC=90°,即∠FEO=90°.
∵点E在⊙O上,
∴FE为⊙O的切线.
(2)∵⊙O的半径为3,∴AO=CO=EO=3.
∵∠EAC=60°,OA=OE,∴∠EOA=60°,
∴∠COD=∠EOA=60°.
∵在Rt△OCD中,∠COD=60°,OC=3,
∴CD=3.
∵在Rt△ACD中,∠ACD=90°,CD=3,AC=6,
∴AD=3.
小专题(九) 证明圆的切线的两种方法
方法1 连半径、证垂直
要证明某直线是圆的切线,当直线与圆有公共点时,可连接圆心与公共点,证明连线与直线垂直即可证得直线是圆的切线.
【例1】 (黄石中考)如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
解:(1)∵AB是⊙O的直径,C在⊙O上,∴∠ACB=90°.
又∵BC=3,AB=5,
∴AC=4.
(2)证明:连接OC.
∵AC是∠DAB的平分线,
∴∠DAC=∠BAC.
又∵AD⊥DC,∴∠ADC=∠ACB=90°.
∴∠DCA=∠B.
又∵OA=OC,∴∠OAC=∠OCA.
∵∠OAC+∠B=90°,
∴∠OCA+∠ACD=∠OCD=90°,即OC⊥CD.
∴DC是⊙O的切线.
INCLUDEPICTURE
"../../../针对训练.TIF"
\
MERGEFORMAT
1.(本溪中考)如图,△ABC中,AB=AC,点E是线段BC延长线上一点,ED⊥AB,垂足为D,ED交线段AC于点F,点O在线段EF上,⊙O经过C,E两点,交ED于点G.
(1)求证:AC是⊙O的切线;
(2)若∠E=30°,AD=1,BD=5,求⊙O的半径.
解:(1)证明:连接CO.
∵AB=AC,
∴∠B=∠ACB.
∵OC=OE,
∴∠OCE=∠E.
∵DE⊥AB,
∴∠BDE=90°.
∴∠B+∠E=90°.∴∠ACB+∠OCE=90°.
∴∠ACO=90°,即AC⊥OC.
∴AC是⊙O的切线.
(2)∵∠E=30°,∴∠OCE=30°.∴∠FCE=120°.
∴∠CFO=30°.∴∠AFD=∠CFO=30°.
∴DF=AD=.
∵BD=5,∴DE=5.
∵OF=2OC,∴EF=3OE=4.
∴OE=,即⊙O的半径为.
2.(枣庄中考)如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB,AB,∠PBA=∠C.
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2,求BC的长.
解:(1)证明:连接OB.
∵AC是⊙O的直径,
∴∠ABC=90°.
∴∠C+∠BAC=90°.
∵OA=OB,
∴∠BAC=∠OBA.
∵∠PBA=∠C,
∴∠PBA+∠OBA=90°,即PB⊥OB.
∴PB是⊙O的切线.
(2)∵⊙O的半径为2,∴OB=2,AC=4.
∵OP∥BC,∴∠BOP=∠OBC=∠C.
又∵∠ABC=∠PBO=90°,∴△ABC∽△PBO.
∴=,即=.∴BC=2.
3.(广安中考)如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=,求⊙O的半径r及sinB.
解:(1)证明:连接OA,OD.
∵点D为CE的下半圆弧的中点,
∴OD⊥BC.
∴∠EOD=90°.
∵AB=BF,OA=OD,
∴∠BAF=∠BFA,∠OAD=∠D.
又∵∠BFA=∠OFD,
∴∠OAD+∠BAF=∠D+∠DFO=90°,
即∠OAB=90°.
∴OA⊥AB.∴AB是⊙O切线.
(2)OF=CF-OC=4-r,OD=r,DF=,
在Rt△DOF中,OD2+OF2=DF2,
即r2+(4-r)2=()2.解得r1=3,r2=1(舍去).
∴OA=3,OF=CF-OC=4-3=1,BO=BF+FO=AB+1.
在Rt△AOB中,AB2+OA2=OB2,
∴AB2+32=(AB+1)2.∴AB=4,OB=5.
∴sinB==.
方法2 作垂直,证半径
当条件中没有指出圆与直线有公共点时,可先过圆心作直线的垂线,再证明垂线段的长和半径相等即可证得直线是圆的切线.
【例2】 (南充中考)如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,OC=1,以点O为圆心,OC为半径作半圆.
(1)求证:AB为⊙O的切线;
(2)如果tan∠CAO=,求cosB的值.
解:(1)证明:作OM⊥AB于M,
∵OA平分∠CAB,OC⊥AC,OM⊥AB,
∴OC=OM.
∴AB是⊙O的切线.
(2)设BM=x,
OB=y,则y2-x2=1,①
∵tan∠CAO=,OC=1,∴AC=AM=3.
∵cosB==,∴=.
∴x2+3x=y2+y.②
由①②可得y=3x-1,∴(3x-1)2-x2=1.
∴x=,y=.∴cosB==.
INCLUDEPICTURE
"../../../针对训练.TIF"
\
MERGEFORMAT
4.如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3.
(1)求证:AC是⊙D的切线;
(2)求线段AC的长.
解:(1)证明:过点D作DF⊥AC于F.
∵AB为⊙D的切线,
∴∠B=90°.
∴AB⊥BC.
∵AD平分∠BAC,DF⊥AC,
∴BD=DF.
∴AC与⊙D相切.
(2)∵BD=DF,DE=DC,
∴Rt△BDE≌Rt△FDC(HL).∴EB=FC.
∵AB=AF,
∴AC=AF+FC=AB+EB=5+3=8.
5.如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M,与AB,AD分别相交于点E,F.求证:CD与⊙O相切.
证明:连接OM,过点O作ON⊥CD,垂足为N.
∵⊙O与BC相切于M,
∴OM⊥BC.
∵在正方形ABCD中,AC平分∠BCD,
又∵ON⊥CD,OM⊥BC,
∴OM=ON.
∴N在⊙O上.
∴CD与⊙O相切.
6.如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.
解:(1)证明:连接OC,作OD⊥PB于D点.
∵⊙O与PA相切于点C,∴OC⊥PA.
∵点O在∠APB的平分线上,OC⊥PA,OD⊥PB,
∴OD=OC.∴直线PB与⊙O相切.
(2)设PO交⊙O于F,连接CF.
∵OC=3,PC=4,∴PO=5,PE=8.
∵⊙O与PA相切于点C,∴∠PCF=∠E.
又∵∠CPF=∠EPC,∴△PCF∽△PEC.
∴CF∶CE=PC∶PE=4∶8=1∶2.
∵EF是直径,∴∠ECF=90°.
设CF=x,则EC=2x.则x2+(2x)2=62.
解得x=.
∴EC=2x=.
3.7 切线长定理
基础题
知识点 切线长定理
1.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是(B)
A.4
B.8
C.4
D.8
2.如图,△MBC中,∠B=90°,∠C=60°,MB=2,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为(C)
A.
B.
C.2
D.3
3.如图,PA,PB是⊙O的切线,切点为A,B,若OP=4,PA=2,则∠AOB的度数为(C)
A.60°
B.90°
C.120°
D.无法确定
4.如图,P为⊙O外一点,PA,PB分别切⊙O于点A,B,CD切⊙O于点E且分别交PA,PB于点C,D,若PA=4,则△PCD的周长为(C)
A.5
B.7
C.8
D.10
5.一个钢管放在V形架内,如图是其截面图,O为钢管的圆心.如果钢管的半径为25
cm,∠MPN=60°,则OP=(A)
A.50
cm
B.25
cm
C.
cm
D.50
cm
6.如图,AB为⊙O的直径,点C在AB的延长线上,CD,CE分别与⊙O相切于点D,E,若AD=2,∠DAC=∠DCA,则CE=2.
7.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,分别交PA,PB于C,D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是.
8.如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠P=60°,OA=2,求BC的长.
解:∵PA,PB是⊙O的切线,∴AP=BP.
又∵∠P=60°,
∴∠PAB=60°.
∵PA是⊙O的切线,
∴∠PAC=90°.
∴∠BAC=90°-60°=30°.
又∵AC是⊙O的直径,
∴∠ABC=90°.
∴BC=AC=OA=2.
9.在一个夹角为120°的墙角放置了一个圆柱体的容器,俯视图如图,在俯视图中圆与两边的墙分别切于B,C两点.(圆柱体容器的直径不易直接测量)
(1)写出此图中相等的线段;
(2)请你设计一种可以通过计算求出直径的测量方法.(写出主要解题过程)
解:(1)根据切线长定理,知AB=AC.
(2)连接OB,OA.
∵∠BAC=120°,∴∠OAB=60°.
在Rt△AOB中,
OB=AB·tan∠OAB=AB.
∴圆的直径为2AB.
即只需测得AB的长,就可求得圆的直径.
中档题
10.如图,一圆内切于四边形ABCD,AB=16,CD=10,则四边形的周长为(B)
A.50
B.52
C.54
D.56
11.如图,△ABC是一张周长为17
cm的三角形纸片,BC=5
cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为(B)
A.12
cm
B.7
cm
C.6
cm
D.随直线MN的变化而变化
12.如图,P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B,C是弧AB上的任意一点,过点C的切线分别交PA、PB于点D、E.
(1)若PA=4,求△PED的周长;
(2)若∠P=40°,求∠AFB的度数.
解:(1)∵DA,DC都是⊙O的切线,∴DC=DA,同理EC=EB.
∵P是⊙O外的一点,PA,PB分别与⊙O相切于点A、B,∴PA=PB.
∴△PED的周长为PD+PE+DE=PD+DC+PE+CE=PA+PB=2PA=8.
即△PDE的周长是8.
(2)连接AB,
∵PA=PB,∴∠PAB=∠PBA.
∵∠P=40°,
∴∠PAB=∠PBA=×(180°-40°)=70°.
∵BF⊥PB,BF为圆的直径,
∴∠ABF=90°-70°=20°,∠FAB=90°.
∴∠AFB=90°-20°=70°.
13.如图,PA,PB分别切⊙O于A,B,连接PO,与AB相交于D,C是⊙O上一点,∠C=60°.
(1)求∠APB的大小;
(2)若PO=20
cm,求△AOB的面积.
解:(1)∵∠C=60°,∴∠AOB=120°.
∵PA,PB分别切⊙O于A,B,
∴∠PAO=∠PBO=90°.
∴∠APB=60°.
(2)∵PA,PB分别切⊙O于A,B,
∴PA=PB.
∴点P在AB的垂直平分线上.
同理,点O在AB的垂直平分线上.
∴PO垂直平分AB.
∵∠APB=60°,∠AOB=120°,
∴∠OPB=∠OPA=30°,∠POB=∠POA=60°.
∵PO=20
cm,∴OB=10
cm.
∴OD=OB·cos∠POB=5
cm.
BD=OB·sin∠POB=5
cm.
∴AB=2BD=10
cm.
∴S△AOB=×10×5=25(cm2).
综合题
14.(贺州中考)如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6
cm,CO=8
cm.
(1)求证:BO⊥CO;
(2)求BE和CG的长.
解:(1)证明:∵AB∥CD,
∴∠ABC+∠BCD=180°.
∵AB,BC,CD分别与⊙O相切于E,F,G,
∴BO平分∠ABC,CO平分∠DCB.
∴∠OBC=∠ABC,∠OCB=∠DCB.
∴∠OBC+∠OCB=(∠ABC+∠DCB)=×180°=90°.
∴∠BOC=90°,∴BO⊥CO.
(2)连接OF,则OF⊥BC,
∵在Rt△BOC中,BO=6
cm,CO=8
cm,
∴BC==10(cm).
易证Rt△BOF∽Rt△BCO.∴=.
∴=,∴BF=3.6
cm.
∵AB,BC,CD分别与⊙O相切,
∴BE=BF=3.6
cm,CG=CF.
∵CF=BC-BF=10-3.6=6.4(cm),
∴CG=CF=6.4
cm.
小专题(十) 圆的切线的性质与判定的综合运用
1.(贵港中考)如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=,AB=12,求半圆O所在圆的半径.
解:(1)证明:连接OD,OA,作OE⊥AB于E,
∵AB=AC,O为BC的中点,
∴∠CAO=∠BAO.
∵OD⊥AC,OE⊥AB,∴OD=OE.
∵AB经过圆O半径的外端,
∴AB是半圆O所在圆的切线.
(2)由cos∠ABC=,AB=12,得OB=8.
由勾股定理,得AO==4.
∵S△AOB=AB·OE=OB·AO,
∴OE==,即半圆O所在圆的半径是.
2.如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
证明:(1)连接OD,BD.
∵AB是⊙O的切线,
∴AB⊥BC,即∠ABC=90°.
∵AB=AD,∴∠ABD=∠ADB.
∵OB=OD,∴∠DBO=∠BDO.
∴∠ABD+∠DBO=∠ADB+∠BDO.
∴∠ADO=∠ABO=90°.
∴AD是半圆O的切线.
(2)连接CD,求证:∠A=2∠CDE.
证明:由(1)知,∠ADO=∠ABO=90°,
∴∠A=360°-∠ADO-∠ABO-∠BOD=180°-∠BOD=∠DOC.
∵AD是半圆O的切线,∴∠ODE=90°.
∴∠ODC+∠CDE=90°.
∵BC是⊙O的直径,∴∠ODC+∠BDO=90°.
∴∠BDO=∠CDE.
∵∠BDO=∠OBD,∠DOC=2∠OBD,
∴∠DOC=2∠BDO.
∴∠DOC=2∠CDE.
∴∠A=2∠CDE.
3.(玉林中考)如图,AB是⊙O的直径,点C,D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA延长线与OC延长线于点E,F,连接BF.
(1)求证:BF是⊙O的切线;
(2)已知圆的半径为1,求EF的长.
解:(1)证明:连接OD,
∵四边形AOCD是平行四边形,OA=OC,
∴四边形AOCD是菱形.
∴△OAD和△OCD都是等边三角形.
∴∠AOD=∠COD=60°.∴∠FOB=60°.
∵EF为切线,∴OD⊥EF.∴∠FDO=90°.
在△FDO和△FBO中,
∴△FDO≌△FBO.∴∠ODF=∠OBF=90°.
∴OB⊥BF.∴BF是⊙O的切线.
(2)在Rt△OBF中,
∵∠FOB=60°,tan∠FOB=,
∴∠E=30°,BF=1×tan60°=.
∵∠E=30°,
∴EF=2BF=2.
4.(西宁中考)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,=,求BE的长.
解:(1)证明:连接OD,∵OB=OD,
∴∠OBD=∠BDO.
∵∠CDA=∠CBD,∴∠CDA=∠ODB.又∵AB是⊙O的直径,∴∠ADB=90°.
∴∠ADO+∠ODB=90°.
∴∠ADO+∠CDA=90°,即∠CDO=90°.
∴OD⊥CD.
∵OD是⊙O半径,∴CD是⊙O的切线.
(2)∵∠C=∠C,∠CDA=∠CBD,
∴△CDA∽△CBD.∴=.
∵=,BC=6,∴CD=4.
∵CE,BE是⊙O的切线,∴BE=DE,BE⊥BC.
∴BE2+BC2=EC2,即BE2+62=(4+BE)2.
解得BE=.
5.已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F,连接DF.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
解:(1)证明:连接OE,
则OB=OE.
∵△ABC是等边三角形,
∴∠ABC=∠C=60°.
∴△OBE是等边三角形.
∴∠OEB=∠C=60°.∴OE∥AC.
∵EF⊥AC,∴∠EFC=90°.
∴∠OEF=∠EFC=90°.∴EF是⊙O的切线.
(2)∵DF是⊙O的切线,∴∠ADF=90°.
设⊙O的半径为r,则BE=r,EC=4-r,
AD=4-2r.
在Rt△ADF中,∵∠A=60°,
∴AF=2AD=8-4r.
∴FC=4-(8-4r)=4r-4.
在Rt△CEF中,∵∠C=60°,
∴EC=2FC.∴4-r=2(4r-4),解得r=.
∴⊙O的半径是.
6.如图,AB是⊙O的直径,点P在⊙O上,且PA=PB,点M是⊙O外一点,MB与⊙O相切于点B,连接OM,过点A作AC∥OM交⊙O于点C,连接BC交OM于点D.
(1)求证:OD=AC;
(2)求证:MC是⊙O的切线;
(3)若MD=8,BC=12,连接PC,求PC的长.
解:(1)证明:∵AC∥OM,
∴△BOD∽△BAC.
∴
==
.
∴OD=AC.
(2)证明:连接OC,∵AC∥OM,
∴∠OAC=∠BOM,∠ACO=∠COM.
∵OA=OC,∴∠OAC=∠ACO.
∴∠BOM=∠COM.
在△OCM和△OBM中,
∴△OCM≌△OBM.
又∵MB是⊙O的切线,∴∠OCM=∠OBM=90°.
∴MC是⊙O的切线.
(3)∵AB是⊙O的直径,∴∠ACB=∠APB=90°,∵AC∥OM,∴OD⊥BC.
∴CD=BD=BC=6.
∴∠OCD+∠MCD=∠CMD+∠MCD=90°,
∴∠OCD=∠CMD.
∵∠OCM=∠CDO=∠CDM=90°,
∴△CDO∽△MDC.
∴CD2=OD·DM.∴OD=.∴OC=.
∴AB=15.∴PA=PB=,AC=9.
过点A作AH⊥PC于点H,∴AH=CH=.
∴PH==6.
∴PC=PH+CH=.
3.8 圆内接正多边形
基础题
知识点1 圆内接正多边形的概念
1.下列说法错误的是(C)
A.圆内接正多边形每个内角都相等
B.圆内接正多边形都是轴对称图形
C.圆内接正多边形都是中心对称图形
D.圆内接正多边形的中心到各边的距离相等
知识点2 圆内接正多边形的有关计算
2.中心角为30°的圆内接正n边形的n等于(B)
A.10
B.12
C.14
D.15
3.(青岛中考)如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=(A)
A.30°
B.35°
C.45°
D.60°
4.如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB等于(B)
A.30°
B.45°
C.55°
D.60°
5.(滨州中考)若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为(B)
A.6,3
B.3,3
C.6,3
D.6,3
6.(西宁中考)一元钱硬币的直径约为24
mm,则用它能完全覆盖住的正六边形的边长最大不能超过(A)
A.12
mm
B.12
mm
C.6
mm
D.6
mm
7.如图,点O是正五边形ABCDE的中心,则∠BAO的度数为54°.
8.(盐城中考)如图,正六边形ABCDEF内接于半径为4的圆,则B,E两点间的距离为8.
9.已知正六边形的边心距为,求正六边形的中心角、边长、周长和面积.
解:如图,连接OB,OC,过点O作OH⊥BC于H,
∵六边形ABCDEF是正六边形,∴∠BOC=×360°=60°.
∵OB=OC,∴△OBC是等边三角形.
∴∠OBC=60°,BC=OB=OC.
∵OH=,∴sin∠OBC===.
∴OB=BC=2.
∴正六边形的周长为2×6=12.
∴S正六边形ABCDEF=6S△OBC=6××2×=6.
∴正六边形的中心角为60°,边长为2,周长为12,面积为6.
知识点3 圆内接正多边形的作图
10.(兰州中考)如图,已知⊙O,用尺规作⊙O的内接正四边形ABCD.(写出结论,不写作法,保留作图痕迹)
解:画圆的一条直径AC,作这条直径的中垂线交⊙O于点B,D,连接AB,BC,CD,DA,得到圆内接正四边形ABCD.如图所示,四边形ABCD即为所求.
中档题
11.(泸州中考)以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是(D)
A.
B.
C.
D.
12.如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是(C)
A.5
B.6
C.7
D.8
13.(滨州中考)若正方形的外接圆半径为2,则其内切圆半径为(A)
A.
B.2
C.
D.1
14.(莱芜中考)正多边形的内切圆与外接圆的周长之比为∶2,则这个正多边形为(B)
A.正十二边形
B.正六边形
C.正四边形
D.正三角形
15.如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若A点的坐标为(-1,0),则点C的坐标为(,-).
16.(威海中考)如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为2.
17.如图,已知等边△ABC内接于⊙O,BD为⊙O内接正十二边形的一边,CD=5
cm,求⊙O的半径R.
解:连接OB,OC,OD,
∵等边△ABC内接于⊙O,BD为⊙O内接正十二边形的一边,
∴∠BOC=×360°=120°,∠BOD=×360°=30°.
∴∠COD=∠BOC-∠BOD=90°.
∵OC=OD,∴∠OCD=45°.
∴OC=CD·cos45°=5×=5(cm).
∴⊙O的半径R=5
cm.
综合题
18.如图1,2,3,…,m中,点M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEF…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是90°,图3中∠MON的度数是72°;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
解:(1)连接OA,OB.
∵正三角形ABC内接于⊙O,
∴AB=BC,∠OAM=∠OBN=30°,
∠AOB=120°.
∵BM=CN,∴AM=BN.
∴△AOM≌△BON(SAS).
∴∠AOM=∠BON.
∴∠AOM+∠BOM=∠BON+∠BOM.
∴∠AOB=∠MON=120°.
(3)∠MON=.
3.9 弧长及扇形的面积
基础题
知识点1 弧长公式及其应用(l=)
1.(云南中考)已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为(C)
A.
B.2π
C.3π
D.12π
2.(自贡中考)一个扇形的半径为8
cm,弧长为π
cm,则扇形的圆心角为(B)
A.60°
B.120°
C.150°
D.180°
3.(包头中考)120°的圆心角对的弧长是6π,则此弧所在圆的半径是(C)
A.3
B.4
C.9
D.18
4.(长春中考)如图,PA,PB是⊙O的切线,切点分别为A,B,若OA=2,∠P=60°,则的长为(C)
A.π
B.π
C.π
D.π
5.(莆田中考)如图,CD为⊙O的弦,直径AB为4,AB⊥CD于点E,∠A=30°,则的长为π(结果保留π).
6.一段圆弧形公路弯道,圆弧的半径为2
km,弯道所对圆心角为10°,一辆汽车从此弯道上驶过,用时20
s,弯道有一块限速警示牌,限速为40
km/h,问这辆汽车经过弯道时有没有超速?(π取3)
解:l==
km.
∴汽车的速度为÷=60(km/h).
∵60
km/h>40
km/h,
∴这辆汽车经过弯道时超速.
知识点2 扇形面积公式及其应用(S==lR)
7.(新疆中考)一个扇形的圆心角是120°,面积为3π
cm2,那么这个扇形的半径是(B)
A.1
cm
B.3
cm
C.6
cm
D.9
cm
8.(资阳中考)钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是(A)
A.π
B.π
C.π
D.π
9.(青岛中考)如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,长为25
cm,贴纸部分的宽BD为15
cm,若纸扇两面贴纸,则贴纸的面积为(B)
A.175π
cm2
B.350π
cm2
C.π
cm2
D.150π
cm2
10.(邵阳中考)如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是π.
11.(河北中考)如图,将长为8
cm的铁丝首尾相接围成半径为2
cm的扇形,则S扇形=4cm2.
中档题
12.(南充中考)如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是(A)
A.π
B.13π
C.25π
D.25
13.(莱芜中考)如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为(B)
A.π
B.2π
C.
D.4π
14.(天水中考)如图,△ABC是等边三角形,曲线CDEF叫做等边三角形的渐开线,其中,,的圆心依次是A,B,C,如果AB=1,那么曲线CDEF的长是4π.
15.(绥化中考)如图,在半径AC为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则图中阴影部分的面积是π-1.
16.(河南中考)如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作交于点C,若OA=2,则阴影部分的面积为-π.
17.(苏州中考改编)如图,在△ABC中,AB=AC.分别以B,C为圆心,BC长为半径在BC下方画弧,设两弧交于点D,与AB,AC的延长线分别交于点E,F,连接AD,BD,CD.若BC=6,∠BAC=50°,求,的长度之和(结果保留π).
解:∵AB=AC,∠BAC=50°,
∴∠ABC=∠ACB=65°.
∵BD=CD=BC,
∴△BDC为等边三角形.
∴∠DBC=∠DCB=60°.
∴∠DBE=∠DCF=55°.
∵BC=6,∴BD=CD=6.
∴l=l==.
∴、的长度之和为+=.
综合题
18.如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,经过点C,求图中阴影部分的面积.
解:令OF交BC于点G,OE交AC于点H,
作OM⊥BC于点M,ON⊥AC于点N.
∵CA=CB,∠ACB=90°,点O为AB的中点,
∴OC=AB=1,四边形OMCN是正方形.
∴OM=ON=.
∴S扇形FOE==.
∵∠GOH=∠MON=90°,∴∠GOM=∠HON.
在△OMG和△ONH中,
∴△OMG≌△ONH(ASA).
∴S四边形OGCH=S正方形OMCN=OM2=()2=.
∴S阴影=-.
小专题(十一) 教材P101随堂练习T1的变式与应用
——和阴影部分面积有关的计算
教材母题:如图,水平放置的一个油管的横截面半径为12
cm,其中有油的部分油面高6
cm,求截面上有油部分的面积(结果精确到0.1
cm2).
【解答】 连接AO,BO,过点O作OC⊥AB于点C.
由题意可知OC=12-6=6(cm),OA=12
cm.
∴sin∠OAC==.
∴∠OAC=30°,AC=6
cm.
∴∠AOC=60°,AB=12
cm.
∴∠AOB=120°.∴S扇形AOB=×π×122=48π(cm2),
S△AOB=AB·OC=×12×6=36(cm2).
∴
S=S扇形AOB-S△AOB=48π-36≈88.4(cm2).
∴截面上有油部分的面积约为88.4
cm2.
【方法归纳】 求阴影部分的面积有以下几种方法:
①直接用公式法;②和差法:计算某部分的面积,可以把这部分看作几部分的和或差,再分别利用公式计算,从而求得阴影部分的面积;③割补法:通过割或补,把不规则图形的面积转化为规则图形的面积;④等积变形法:先利用平移、旋转、对称等全等变换,将不规则图形的面积转化为一个和它面积相等的规则图形的面积,再利用公式计算.
INCLUDEPICTURE
"../../../针对训练.TIF"
\
MERGEFORMAT
1.(重庆中考)如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=,则图中阴影部分的面积是(A)
A.
B.+
C.
D.+
2.(枣庄中考)如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则阴影部分的面积为(D)
A.2π
B.π
C.
D.
3.(资阳中考)如图,在Rt△ABC中,∠ACB=90°,AC=2,以点B为圆心,BC的长为半径作弧,交AB于点D,若点D为AB的中点,则阴影部分的面积是(A)
A.2-π
B.4-π
C.2-π
D.π
4.(内江中考)如图,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为(C)
A.π-4
B.π-1
C.π-2
D.-2
5.如图,在矩形ABCD中,CD=1,∠DBC=30°.若将BD绕点B旋转后,点D落在DC延长线上的点E处,点D经过的路径,则图中阴影部分的面积是(B)
A.-
B.-
C.-
D.-
6.如图,三个小正方形的边长都为1,则图中阴影部分面积的和是(B)
A.
B.
C.
D.
7.如图,半径为2
cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为(A)
A.(-1)cm2
B.(+1)cm2
C.1
cm2
D.
cm2
8.(襄阳中考)如图,AB是半圆O的直径,点C,D是半圆O的三等分点,若弦CD=2,则图中阴影部分的面积为π.
9.(遵义中考)如图,在圆心角为90°的扇形OAB中,半径OA=2
cm,C为的中点,D,E分别是OA,OB的中点,则图中阴影部分的面积为(π+-)cm2.
10.(淮安中考)如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF.
(1)直接写出点F的坐标;
(2)求线段OB的长及图中阴影部分的面积.
解:(1)F(-2,0).
(2)连接AC交OB于点M.
∵四边形OABC为菱形,∴OC=OA,AC⊥OB.
∵OA=2,∠COA=60°,
∴△AOC为等边三角形.
∴AC=2,OM=,OB=2.
∴S阴影=S扇形OEB-2S△BOC=-2××2×1=4π-2.
11.(钦州中考)如图,点B,C,D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.
(1)求证:AC是⊙O的切线;
(2)求弦BD的长;
(3)求图中阴影部分的面积.
解:(1)证明:连接OC,交BD于点E.
∵∠CDB=30°,
∴∠BOC=60°.
∵∠OBD=30°,
∴∠OEB=90°.
∵AC∥BD,∴AC⊥OC.
∴AC是⊙O的切线.
(2)在Rt△OBE中,OB=6,∠OBD=30°,
∴OE=OB=3.
∴BE=3.∴BD=2BE=6.
(3)∵OE=EC=3,BE=ED,∠OEB=∠CED=90°,
∴△OBE≌△CDE(SAS).∴S△OBE=S△DEC.
∴S阴影=S扇形OBC==6π.
12.(襄阳中考)如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连接EF,CG.
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的,与线段CG所围成的阴影部分的面积.
解:(1)证明:∵四边形ABCD是正方形,
∴AB=BC=AD=2,
∠ABC=90°.
∵△BEC绕点B逆时针旋转90°得△BFA,
∴△ABF≌△CBE.
∴∠FAB=∠ECB,∠ABF=∠CBE=90°,AF=CE.
∴∠AFB+∠FAB=90°.
∵线段AF绕点F顺时针旋转90°得线段FG,
∴∠AFB+∠CFG=∠AFG=90°,AF=FG.
∴∠CFG=∠FAB=∠ECB.∴EC∥FG.
∵AF=EC,AF=FG,∴EC=FG.
∴四边形EFGC是平行四边形.∴EF∥CG.
(2)∵△ABF≌△CBE,∴FB=BE=AB=1.
∴AF==.
在△FEC和△CGF中,∵EC=GF,∠ECF=∠CFG,FC=CF,∴△FEC≌△CGF.
∴S△FEC=S△CGF.
∴S阴影=S扇形BAC+S△ABF+S△FGC-S扇形FAG
=+×2×1+×(1+2)×1-
=-.
章末复习(三) 圆
基础题
知识点1 圆的有关概念
1.下列命题中正确的有(A)
①弦是圆上任意两点之间的部分;②半径是弦;③直径是最长的弦;④弧是半圆,半圆是弧.
A.1个
B.2个
C.3个
D.4个
2.如图,在△ABC中,∠ACB=90°,∠A=40°,以点C为圆心,CB为半径的圆交AB于点D,连接CD,则∠ACD=(A)
A.10°
B.15°
C.20°
D.25°
知识点2 圆的对称性
3.下列四个图形中,既是轴对称图形,又是中心对称图形的是(C)
A.等边三角形
B.平行四边形
C.圆
D.正五边形
4.如图,AB是⊙O的直径,点C在⊙O上,∠AOC=40°,D是的中点,则∠ACD=125°.
知识点3 垂径定理
5.如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合),连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=(B)
A.4
B.5
C.5.5
D.6
6.(六盘水中考)赵州桥是我国建筑史上的一大创举,它距今约1
400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R=25米.
知识点4 圆周角定理及其推论
7.如图,已知A,B均为⊙O上一点,若∠AOB=80°,则∠ACB=(D)
A.80°
B.70°
C.60°
D.40°
8.如图是一个圆形人工湖的平面图,弦AB是湖上的一座桥,已知桥长100
m,测得圆周角∠ACB=30°,则这个人工湖的直径为200m.
9.如图,∠DAE是⊙O的内接四边形ABCD的一个外角,且∠DAE=∠DAC.求证:DB=DC.
证明:∵∠DAE是⊙O的内接四边形ABCD的一个外角,
∴∠DAE=∠DCB.
又∵∠DAE=∠DAC,
∴∠DCB=∠DAC.
又∵∠DAC=∠DBC,
∴∠DCB=∠DBC.
∴DB=DC.
知识点5 三角形的外接圆与内切圆
10.如图,点O是△ABC的内心,∠A=62°,则∠BOC等于(D)
A.59°
B.31°
C.124°
D.121°
11.如图,已知等腰△ABC.
(1)用直尺和圆规作△ABC的外接圆;
(2)设△ABC的外接圆的圆心为点O,若∠BOC=128°,求∠BAC的度数.
解:(1)如图.
(2)在优弧BC上任取一点D,连接BD,CD.
∵∠BOC=128°,
∴∠BDC=∠BOC=64°.
∴∠BAC=180°-∠BDC=116°.
知识点6 点、直线与圆的位置关系
12.(白银中考)已知⊙O的半径是6
cm,点O到同一平面内直线l的距离为5
cm,则直线l与⊙O的位置关系是(A)
A.相交
B.相切
C.相离
D.无法判断
13.如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的值可以是下列选项中的(B)
A.3
B.4
C.5
D.6
知识点7 切线的性质与判定
14.(益阳中考)如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为115°.
15.如图,直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为2.
16.(宿迁中考)如图1,在△ABC中,点D在边BC上,∠B∶∠C∶∠ADB=1∶2∶3,⊙O是△ABD的外接圆.
图1
图2
(1)求证:AC是⊙O的切线;
(2)当BD是⊙O的直径时(如图2),求∠CAD的度数.
解:(1)证明:连接AO,延长AO交⊙O于点E,则AE为⊙O的直径,连接DE.
∵∠B∶∠C∶∠ADB=1∶2∶3,∠ADB=∠C+∠CAD,∴∠B=∠CAD.
∵AE为⊙O的直径,∴∠ADE=90°.
∴∠EAD=90°-∠E.
∵∠E=∠B,∴∠E=∠B=∠CAD.
∴∠EAD+∠CAD=90°,即∠EAD+∠CAD=90°.
∴EA⊥AC,∴AC是⊙O的切线.
(2)∵BD是⊙O的直径,
∴∠BAD=90°.∴∠B+∠ADB=90°.
∵∠B∶∠C∶∠ADB=1∶2∶3,
∴4∠B=90°.∴∠B=22.5°.
由(1)知∠ABC=∠CAD,∴∠CAD=22.5°.
知识点8 与圆有关的计算
17.(遵义中考)如图,半圆的圆心为点O,直径AB的长为12,C为半圆上一点,∠CAB=30°,的长是(D)
A.12π
B.6π
C.5π
D.4π
18.已知扇形的圆心角为60°,半径长为12,则扇形的面积为(D)
A.π
B.2π
C.3π
D.24π
19.如图,已知⊙O的周长等于8π
cm,则圆内接正六边形ABCDEF的边心距OM的长为(B)
A.2
cm
B.2
cm
C.4
cm
D.4
cm
20.如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=2,点D是AB的中点,连接DO并延长交⊙O于点P,过点P作PF⊥AC于点F.
(1)求劣弧PC的长;(结果保留π)
(2)求阴影部分的面积.(结果保留π)
解:(1)∵点D是AB的中点,PD经过圆心,
∴PD⊥AB.
∵∠A=30°,
∴∠POC=∠AOD=60°,
OA=2OD.
∵PF⊥AC,
∴∠OPF=30°.
∴OF=OP.
∵OA=OC,AD=BD,
∴BC=2OD.
∴OA=BC=2.
∴⊙O的半径为2.
∴劣弧PC的长为=π.
(2)∵OF=OP,
∴OF=1.
∴PF==.
∴S阴影=S扇形-S△OPF=-×1×
=π-.
中档题
21.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长等于(C)
A.
B.
C.8
D.6
22.(巴彦淖尔中考)如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为(A)
A.-
B.-π
C.2-
D.-
23.已知⊙O的半径为r,其内接正六边形,正四边形,正三角形的边长分别为a,b,c,则a∶b∶c的值为(C)
A.1∶2∶3
B.3∶2∶1
C.1∶∶
D.∶∶1
24.如图,圆内接△ABC的外角∠ACH的平分线与圆交于D点,DP⊥AC,垂足是点P,DH⊥BH,垂足是点H,下列结论:①CH=CP;②AD=DB;③AP=BH;④DH为圆的切线.其中一定成立的是(D)
A.①②④
B.①③④
C.②③④
D.①②③
25.如图,一块等边三角形的木板,边长为1,现将木板沿水平线翻滚,那么B点从开始至结束所走过的路径长度为.
26.已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴,y轴分别交于点A,B,点A的坐标为(,0),⊙M的切线OC与直线AB交于点C.则∠ACO=30°.
27.如图,在⊙O中,AB为直径,点B为的中点,直径AB交弦CD于点E,CD=2,AE=5.
(1)求⊙O半径r的值;
(2)点F在直径AB上,连接CF,当∠FCD=∠DOB时,求AF的长.
解:(1)∵AB为直径,点B为的中点,CD=2,
∴AB⊥CD,DE=CD=.
在Rt△ODE中,
∵OD=r,OE=5-r,DE=,
∴r2=(5-r)2+()2,解得r=3.
(2)∵由(1)知,OE=AE-AO=5-3=2,
∴tan∠FCE=tan∠DOB==.
在Rt△FCE中,∵tan∠FCE===,
∴EF=.
∴AF=AE-EF=5-=.
28.(葫芦岛中考)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为点F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=,求图中阴影部分的面积.
解:(1)证明:连接AD,OD,∵AB为直径,
∴∠ADB=90°.
∴AD⊥BC.
∵AC=AB,
∴点D为线段BC的中点.
∵点O为AB的中点,
∴OD为△BAC的中位线.∴OD∥AC.
∵DF⊥AC,∴OD⊥DF.∴DF是⊙O的切线.
(2)在Rt△CFD中,CF=1,DF=,
∴tanC==,CD=2.∴∠C=60°.
∵AC=AB,∴△ABC为等边三角形.∴AB=4.
∵OD∥AC,∴∠DOG=∠BAC=60°.
∴DG=OD·tan∠DOG=2.
∴S阴影=S△ODG-S扇形OBD
=DG·OD-πOB2
=2-π.
综合题
29.如图所示,BC是半圆O的直径,AD⊥BC,垂足为点D,弧长等于弧长,BF与AD,AO分别交于点E,G.求证:
(1)∠DAO=∠FBC;
(2)AE=BE.
证明:(1)连接CF.
∵等于,O为圆心,
∴点G是BF的中点,OG⊥BF.
∵BC是半圆O的直径,
∴CF⊥BF.
∴OG∥CF.
∴∠AOB=∠FCB.
∴∠DAO=90°-∠AOB,∠FBC=90°-∠FCB.
∴∠DAO=∠FBC.
(2)连接AC,AB.
∵l=l,
∴∠BCA=∠ACF=∠ABF.
∵BC为圆的直径,
∴∠BAC=90°.
∴∠ABC+∠ACB=90°.
又∵AD⊥BC,∴∠ADB=90°.
∴∠ABC+∠BAD=90°.
∴∠BAD=∠BCA.
∴∠ABF=∠BAD,
即BE=AE.
3.1 圆
基础题
知识点1 圆的有关概念
1.下列说法正确的是(D)
A.半圆是弧,弧也是半圆
B.过圆上任意一点只能作一条弦,且这条弦是直径
C.弦是直径
D.直径是圆中最长的弦
2.下列条件中,能画唯一圆的是(B)
A.以已知点O为圆心
B.以点O为圆心,2
cm为半径
C.以1
cm为半径
D.经过已知点A,且半径为2
cm
3.已知⊙O的直径AB=6
cm,则圆上任意一点到圆心的距离等于(C)
A.2
cm
B.2.5
cm
C.3
cm
D.无法确定
4.如图,圆中有1条直径,3条弦,圆中以A为一个端点的优弧有4条,劣弧有4条.
5.如图,⊙O的半径是5,∠AOB=60°,则AB=5.
6.孙老师上数学课时忘记了带圆规,但他手里有一根小细绳,你能帮他在黑板上画一个圆吗?并说明理由.
解:能.将小细绳绕着它的一个端点,旋转一周,另一个端点走过的路线即为一个圆,理由:圆可以看成是到定点的距离等于定长的所有点组成的图形.
知识点2 点与圆的位置关系
7.(湘西中考)⊙O的半径为5
cm,点A到圆心O的距离OA=3
cm,则点A与⊙O的位置关系为(B)
A.点A在圆上
B.点A在圆内
C.点A在圆外
D.无法确定
8.已知⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是(A)
A.点P在⊙O内
B.点P的⊙O上
C.点P在⊙O外
D.点P在⊙O上或⊙O外
9.已知⊙O的半径为3
cm,⊙O所在的平面内一点P,当PO=3__cm时,点P在⊙O上;当PO<3__cm时,点P在⊙O内;当PO>3__cm时,点P在⊙O外.
10.在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,r=3为半径作圆,判断A,B两点和⊙C的位置关系.
解:∵∠C=90°,AC=4,AB=5,∴BC=3.
∵AC=4>r,∴点A在⊙C外.
∵BC=3=r,∴点B在⊙C上.
中档题
11.下列命题,其中正确的有(A)
①两个端点能够重合的弧是等弧;②面积相等的两个圆是等圆;③弦是圆上任意两点之间的部分;④同圆或等圆中,劣弧比优弧短.
A.1个
B.2个
C.3个
D.4个
12.(宜昌中考)在公园的O处附近有E,F,G,H四棵树,位置如图所示(图中小正方形的边长均相等),现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E,F,G,H四棵树中需要被移除的为(A)
A.E,F,G
B.F,G,H
C.G,H,E
D.H,E,F
13.如图,在△ABC中,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E两点,并连接BD,DE.若∠A=30°,AB=AC,则∠BDE的度数为(C)
A.45°
B.52.5°
C.67.5°
D.75°
14.矩形ABCD中,AB=3,BC=4,以点A为圆心画圆,使B,C,D三点中至少有一点在⊙A内,且至少有一点在⊙A外,则⊙A的半径r的取值范围为(D)
A.r>3
B.r<4
C.r<5
D.3<r<5
15.(永州中考)如图,在⊙O中,A,B是圆上的两点,已知∠AOB=40°,直径CD∥AB,连接AC,则∠BAC=35°.
16.在Rt△ABC中,∠C=90°,∠A=30°,以点C为圆心,CB为半径画圆,则斜边AB的中点D与⊙C的位置关系是点D在⊙C上.
17.如图,数轴上半径为1的⊙O从原点O开始以每秒1个单位的速度向右运动,同时,距原点右边7个单位有一点P以每秒2个单位的速度向左运动,经过2或秒后,点P在⊙O上.
18.如图,小虎牵着小狗上街,小虎的手臂与绳共2.5
m(手臂与拉直的绳子在一条直线上),手臂肩部距地面1.5
m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
解:小狗在地面上环绕的圆的半径为
=2.0(m),
故小狗在平整的地面上活动的最大区域是以2.0
m为半径的圆.
如图:
综合题
19.(杭州中考)如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′·OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
图1 图2
解:设OA交⊙O于M,连接BM.
∵OA′·OA=r2,r=4,OA=8,∴OA′=2.
∵OB′·OB=r2,r=4,OB=4,
∴OB′=4,即点B和B′重合.
∵∠BOA=60°,OB=OM,∴△OBM为等边三角形.
∵点A′为OM的中点,∴B′A′⊥OM.
在Rt△OA′B′中,sin∠A′OB′=,
∴A′B′=4sin60°=2.
3.2 圆的对称性
基础题
知识点1 圆的对称性
1.下列语句中,不正确的是(C)
A.圆是轴对称图形,任意一条直径所在的直线都是它的对称轴
B.圆既是轴对称图形,又是中心对称图形
C.当圆绕它的圆心旋转89°57′时,不会与原来的圆重合
D.圆的对称轴有无数条,对称中心只有一个
2.(泰安中考)下列四个图形:
其中是轴对称图形,且对称轴的条数为2的图形的个数是(C)
A.1
B.2
C.3
D.4
3.如图是两个同心圆,其中两条直径互相垂直,大圆的半径是2,则其阴影部分的面积之和为2π(结果保留π).
知识点2 圆心角、弧及弦之间的关系
4.在同圆或等圆中,如果=,那么AB和CD的关系是(B)
A.AB>CD
B.AB=CD
C.AB<CD
D.AB=2CD
5.(兰州中考)如图,在⊙O中,若点C是的中点,∠A=50°,则∠BOC=(A)
A.40°
B.45°
C.50°
D.60°
6.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,则下列结论中正确的有(D)
①=;②=;③AC=BD;④∠BOD=∠AOC.
A.1个
B.2个
C.3个
D.4个
7.如图所示,在⊙O中,AC,BC是弦,根据条件填空:
(1)若AC=BC,则=,∠AOC=∠BOC;
(2)若=,则AC=BC,∠AOC=∠BOC;
(3)若∠AOC=∠BOC,则=,AC=BC.
8.如图,在⊙O中,=,若∠AOB=40°,则∠COD=40°.
9.如图,已知:在⊙O中,M,N分别是半径OA,OB的中点,且CM⊥OA,DN⊥OB.求证:=.
证明:连接OC,OD,则OC=OD.
∵M,N分别是半径OA,OB的中点,
∴OM=ON.
∵CM⊥OA,DN⊥OB,
∴∠OMC=∠OND=90°.
在Rt△OMC和Rt△OND中,
∴Rt△OMC≌Rt△OND(HL).
∴∠MOC=∠NOD.∴=.
中档题
10.下列说法:①等弧对等弦;②等弦对等弧;③等弦所对的圆心角相等;④相等的圆心角所对的弧相等;⑤等弧所对的圆心角相等.其中正确的个数为(B)
A.1
B.2
C.3
D.4
11.形如半圆形的量角器直径为4
cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的两个端点P、Q,线段PQ交y轴于点A,则点A的坐标为(B)
A.(-1,)
B.(0,)
C.(,0)
D.(1,)
12.如图,扇形OAB的圆心角为90°,点C,D是的三等分点,半径OC,OD分别与弦AB交于点E,F,下列说法错误的是(A)
A.AE=EF=FB
B.AC=CD=DB
C.EC=FD
D.∠DFB=75°
13.如图,在⊙O中,=2,则下列结论正确的是(C)
A.AB>2CD
B.AB=2CD
C.AB<2CD
D.以上都不正确
14.如图,已知AB是⊙O的直径,C,D,E,F,G是上的点,且有=====,则∠OCG=30°.
15.(黄石中考)如图,A,B是⊙O上的两点,∠AOB=120°,C是的中点.
(1)求证:AB平分∠OAC;
(2)延长OA至P使得AP=OA,连接PC,若⊙O的半径R=1,求PC的长.
解:(1)证明:连接OC.
∵∠AOB=120°,C是的中点,
∴∠AOC=∠BOC=60°.
又∵OA=OC=OB,
∴△AOC、△BOC是等边三角形.
∴OA=OB=BC=AC.
∴四边形AOBC是菱形.
∴AB平分∠OAC.
(2)∵OA=AP,OA=AC,∴AP=AC.
又∵∠CAO=∠ACO=60°,
∴∠APC=30°,∠OCP=90°.
∴PC=OC=.
综合题
16.我们学习了“弧、弦、圆心角的关系”,实际上我们还可以得到“圆心角、弧、弦、弦心距之间的关系”如下:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们对应的其余各组量也相等[弦心距指从圆心到弦的距离(如图1中的OC、OC′),弦心距也可以说成圆心到弦的垂线段的长度].请直接运用圆心角、弧、弦、弦心距之间的关系解答下列问题:
如图2,O是∠EPF的平分线上一点,以点O为圆心的圆与角的两边分别交于点A,B,C,D.
(1)求证:AB=CD;
(2)若角的顶点P在圆上,上述结论还成立吗?若不成立,请说明理由;若成立,请加以证明.
解:(1)证明:过O作OM⊥AB于M,ON⊥CD于N,则∠OMB=∠OND=90°.
∵PO平分∠EPF,∴OM=ON.
∵OM,ON分别是弦AB,CD的弦心距,
∴AB=CD.
(2)上述结论成立.
证明:当点P在⊙O上时,由(1)知OM=ON,
∵OM,ON分别是弦AB,CD的弦心距,
∴PB=PD,即AB=CD.
3.3 垂径定理
基础题
知识点1 垂径定理
1.(黄石中考)如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=(A)
A.5
B.7
C.9
D.11
2.如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16
cm,OC=6
cm,则⊙O的半径为(B)
A.
cm
B.10
cm
C.8
cm
D.
cm
3.(三明中考)如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是(A)
A.2
B.3
C.4
D.5
4.(黑龙江中考)如图,⊙O的直径CD=10
cm,AB是⊙O的弦,且AB⊥CD,垂足为P,AB=8
cm,则sin∠OAP的值是(C)
A.
B.
C.
D.
5.(广元中考)如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是(B)
A.CE=DE
B.AE=OE
C.=
D.△OCE≌△ODE
知识点2 垂径定理的推论
6.下列说法错误的是(C)
A.垂直于弦的直径平分弦
B.垂直于弦的直径平分弦所对的弧
C.平分弦的直径平分弦所对的弧
D.平分弧的直径垂直平分弧所对的弦
7.如图,AB是⊙O的弦,OC为半径,与AB交于点D,且AD=BD,已知AB=6
cm,OD=4
cm,则DC的长为(D)
A.5
cm
B.2.5
cm
C.2
cm
D.1
cm
知识点3 垂径定理的应用
8.如图是一个圆弧形门拱,拱高AB=1
m,跨度CD=4
m,那么这个门拱的半径为(B)
A.2
m
B.2.5
m
C.3
m
D.5
m
9.(东营中考)如图,水平放置的圆柱形排水管道的截面直径是1
m,其中水面的宽AB为0.8
m,则排水管内水的深度为0.8m.
10.如图所示,某窗户由矩形和弓形组成,已知弓形的跨度AB=3
m,弓形的高EF=1
m,现计划安装玻璃,请帮工程师求出所在⊙O的半径r.
解:∵弓形的跨度AB=3
m,EF为弓形的高,
∴OE⊥AB.
∴AF=AB=
m.
∵所在⊙O的半径为r,弓形的高EF=1
m,
∴AO=r,OF=r-1.
在Rt△AOF中,AO2=AF2+OF2,
即r2=()2+(r-1)2.解得r=.
故r=
m.
中档题
11.如图,⊙O的弦AB,AC的夹角为50°,M,N分别为和的中点,OM,ON分别交AB,AC于E,F,则∠MON的度数为(C)
A.110°
B.120°
C.130°
D.100°
12.如图,小明家凉台呈圆弧形,凉台的宽度AB为8
m,凉台的最外端C点离AB的距离CD为2
m,则凉台所在圆的半径为(B)
A.4
m
B.5
m
C.6
m
D.7
m
13.如图,将半径为2
cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为(C)
A.2
cm
B.
cm
C.2
cm
D.2
cm
14.CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=8,则BE的长是(C)
A.8
B.2
C.2或8
D.3或7
15.(黔西南中考)如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,若CD=6,BE=1,则⊙O的直径为10.
16.(绍兴中考)如图1,小敏利用课余时间制作了一个脸盆架,图2是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40
cm,脸盆的最低点C到AB的距离为10
cm,则该脸盆的半径为25cm.
图1
图2
17.(湖州中考)已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.
解:(1)证明:作OE⊥AB,垂足为E,
则AE=BE,CE=DE,
∴AE-CE=BE-DE,
即AC=BD.
(2)由(1)可知,OE⊥AB,OE⊥CD,
连接OC,OA.
∵OE=6,
∴CE===2,
AE===8.
∴AC=AE-CE=8-2.
综合题
18.如图,某地有一座圆弧形拱桥,桥下水面宽度AB为7.2
m,拱高CD为2.4
m.
(1)求拱桥的半径;
(2)现有一艘宽3
m,船舱顶部为长方形并高出水面2
m的货船要经过这里,问此货船能顺利通过拱桥吗?
解:(1)连接OB.
∵OC⊥AB,
∴D为AB的中点.
∵AB=7.2
m,
∴BD=AB=3.6
m.
设OB=OC=r,则OD=(r-2.4)m.
在Rt△BOD中,根据勾股定理,得
r2=(r-2.4)2+3.62,解得r=3.9.
∴拱桥的半径为3.9
m.
(2)令船舱顶部两点分别分M,N(CN在M的右边),连接ON.
∵CD=2.4
m,船舱顶部为长方形并高出水面2
m,∴CE=2.4-2=0.4(m).
∴OE=r-CE=3.9-0.4=3.5(m).
在Rt△OEN中,EN2=ON2-OE2=3.92-3.52=2.96(m2),
∴EN=(m),
MN=2EN=2×≈3.44
m>3
m.
∴此货船能顺利通过这座拱桥.
3.4 圆周角和圆心角的关系
第1课时 圆周角定理及其推论1
基础题
知识点1 圆周角的概念
1.(柳州中考)下列四个图中,∠x是圆周角的是(C)
A B
C
D
2.如图,图中的圆周角有(C)
A.10个
B.11个
C.12个
D.13个
知识点2 圆周角定理
3.(温州中考)如图,已知A,B,C在⊙O上,为优弧,下列选项中与∠AOB相等的是(A)
A.2∠C
B.4∠B
C.4∠A
D.∠B+∠C
4.(济宁中考)如图,在⊙O中,=,∠AOB=40°,则∠ADC的度数是(C)
A.40°
B.30°
C.20°
D.15°
5.如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是(A)
A.25°
B.30°
C.40°
D.50°
6.(娄底中考)如图,将直角三角板60°角的顶点放在圆心O上,斜边和一直角边分别与⊙O相交于A,B两点,P是优弧AB上任意一点(与A,B不重合),则∠APB=30度.
知识点3 圆周角定理的推论1
7.(自贡中考)如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是(C)
A.15°
B.25°
C.30°
D.75°
8.(百色中考)如图,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=65°.
9.如图,已知A,B,C,D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD,AD.求证:DB平分∠ADC.
证明:∵AB=BC,
∴=.
∴∠ADB=∠BDC.
∴DB平分∠ADC.
中档题
10.(巴彦淖尔中考)如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=40°,则∠ABD与∠AOD分别等于(B)
A.40°,80°
B.50°,100°
C.50°,80°
D.40°,100°
11.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为(B)
A.15°
B.28°
C.29°
D.34°
12.(泰安中考)如图,点A,B,C是⊙O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于(B)
A.12.5°
B.15°
C.20°
D.22.5°
13.如图,△ABC内接于⊙O,若∠OAB=28°,则∠C的大小为62°.
14.(临夏中考)如图,在⊙O中,弦AC=2,点B是圆上一点,且∠ABC=45°,则⊙O的半径R=.
15.如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=6,求tan∠DEB的值.
解:(1)连接OB,
∵OD⊥AB,∴=.
∴∠BOD=∠AOD=52°.
∴∠DEB=∠BOD=26°.
(2)∵OD⊥AB,OC=3,OA=6,
∴OC=OA,即∠OAC=30°.
∴∠AOC=60°.
∴∠DEB=∠AOC=30°.
∴tan∠DEB=.
16.如图,在⊙O中,AB=AC,∠CBD=30°,∠BCD=20°,试求∠BAC的度数.
解:连接OB,OC,OD.
∵∠BOD=2∠BCD,∠COD=2∠CBD,∠CBD=30°,
∠BCD=20°,
∴∠COD=60°,∠BOD=40°.
∴∠BOC=100°,
∠BAC=∠BOC=50°.
综合题
17.(台州中考)如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
解:(1)∵BC=DC,
∴=.
∴∠BAC=∠CAD=∠CBD.
∵∠CBD=39°,
∴∠BAC=∠CAD=39°.
∴∠BAD=∠BAC+∠DAC=78°.
(2)证明:∵EC=BC,
∴∠CBE=∠CEB.
∵∠CBE=∠1+∠CBD,∠CEB=∠2+∠BAC,
∴∠1+∠CBD=∠2+∠BAC.
又∵∠BAC=∠CBD,∴∠1=∠2.
第2课时 圆周角定理的推论2、3
基础题
知识点1 圆周角定理的推论2
1.(湖州中考)如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是(C)
A.35°
B.45°
C.55°
D.65°
2.(台州中考)从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是(B)
3.(玉林中考)如图,CD是⊙O的直径,已知∠1=30°,则∠2=(C)
A.30°
B.45°
C.60°
D.70°
4.(常州中考)如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M,N,量得OM=8
cm,ON=6
cm,则该圆玻璃镜的半径是(B)
A.
cm
B.5
cm
C.6
cm
D.10
cm
5.(眉山中考)如图,A,D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC=(B)
A.64°
B.58°
C.72°
D.55°
6.如图,在半径为5
cm的⊙O中,AB为直径,∠ACD=30°,求弦BD的长.
解:∵AB为直径,
∴∠ADB=90°.
又∵∠ABD=∠ACD=30°,
∴BD=AB·cos∠ABD=10×=5(cm).
知识点2 圆周角定理的推论3
7.(杭州中考)圆内接四边形ABCD中,已知∠A=70°,则∠C=(D)
A.20°
B.30°
C.70°
D.110°
8.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是(B)
A.115°
B.105°
C.100°
D.95°
9.(常德中考)如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为(D)
A.50°
B.80°
C.100°
D.130°
10.在圆内接四边形ABCD中,若∠A∶∠B∶∠C=1∶2∶5,则∠B的度数是(C)
A.30°
B.45°
C.60°
D.120°
11.(来宾中考)如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=110°,则∠α=140°.
中档题
12.(达州中考)如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为(C)
A.
B.2
C.
D.
13.(烟台中考)如图,Rt△ABC的斜边AB与量角器的直径恰好重合,B点与0刻度线的一端重合,∠ABC=40°,射线CD绕点C转动,与量角器外沿交于点D,若射线CD将△ABC分割出以BC为边的等腰三角形,则点D在量角器上对应的度数是(D)
A.40°
B.70°
C.70°或80°
D.80°或140°
14.(无锡中考)如图,AB是半圆O的直径,C,D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
解:(1)∵OD∥BC,
∴∠DOA=∠B=70°
又∵OA=OD,
∴∠DAO=∠D=55°.
∵AB是直径,∴∠C=90°.∴∠CAB=20°.
∴∠CAD=35°.
(2)∵∠C=90°,AB=4,AC=3,∴BC=.
∵O是AB中点,OD∥BC,∴OE==.
∴DE=2-.
15.(温州中考)如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1=∠F;
(2)若sinB=,EF=2,求CD的长.
解:(1)证明:连接DE,
∵BD是⊙O的直径,
∴∠DEB=90°.
∵E是AB的中点,
∴DA=DB.
∴∠1=∠B.
∵∠B=∠F,∴∠1=∠F.
(2)∵∠1=∠F,
∴AE=EF=2.
∴AB=2AE=4.
在Rt△ABC中,AC=AB·sinB=4,
∴BC==8.
设CD=x,则AD=BD=8-x.
∵AC2+CD2=AD2,即42+x2=(8-x)2,
∴x=3,即CD=3.
综合题
16.(1)如图1,PA,PB是⊙O的两条弦,AB为直径,C为的中点,弦CD⊥PA于点E,写出AB与AC的数量关系,并证明;
(2)如图2,PA,PB是⊙O的两条弦,AB为弦,C为劣弧的中点,弦CD⊥PA于E,写出AE,PE与PB的数量关系,并证明.
解:(1)AB=AC.
证明:∵AB为直径,C为的中点,
∴∠ACB=90°,AC=BC.
∴AB=AC.
(2)AE=PB+PE.
证明:在AE上截取AF=BP,连接AC,BC,FC,PC.
∵C为劣弧的中点,即=,
∴AC=BC.
在△CAF和△CBP中,
,
∴△CAF≌△CBP.
∴CF=CP.
又∵CD⊥PA,
∴EF=EP.
∴AE=AF+EF=PB+PE.
小专题(八) 与圆的基本性质有关的计算与证明
1.如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.
(1)求∠B的大小;
(2)已知圆心O到BD的距离为3,求AD的长.
解:(1)∵∠CAB=∠CDB,∠CAB=40°,∴∠CDB=40°.
又∵∠APD=65°,
∴∠B=∠APD-∠CDB=25°.
(2)过点O作OE⊥BD于点E,则OE=3,BE=DE.
又∵O是AB的中点,
∴OE是△ABD的中位线.
∴AD=2OE=6.
2.(南京中考)A,B是⊙O上的两个定点,P是⊙O上的动点(P不与A,B重合),我们称∠APB是⊙O上关于点A,B的滑动角.已知∠APB是⊙O上关于点A,B的滑动角.
(1)若AB是⊙O的直径,则∠APB=90°;
(2)如图,若⊙O的半径是1,AB=,求∠APB的度数.
解:连接OA,OB,AB.
∵OA=OB=1,AB=,
∴OA2+OB2=AB2.
∴∠AOB=90°.
∴∠APB=∠AOB=45°.
3.如图,AB是⊙O的直径,C,D两点在⊙O上,若∠C=45°.
(1)求∠ABD的度数;
(2)若∠CDB=30°,BC=3,求⊙O的半径.
解:(1)∵∠C=45°,
∴∠A=∠C=45°.
∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠ABD=45°.
(2)连接AC.
∵AB是⊙O的直径,
∴∠ACB=90°.
∵∠CAB=∠CDB=30°,BC=3,
∴AB=6.
∴⊙O的半径为3.
4.(宁夏中考)如图,已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2,求CD的长.
解:(1)证明:∵ED=EC,
∴∠EDC=∠C.
∵∠EDC=∠B,∴∠B=∠C.∴AB=AC.
(2)连接AE.
∵AB为直径,∴AE⊥BC.
由(1)知AB=AC,∴BE=CE=BC=.
∵∠C=∠C,∠EDC=∠B,∴△CDE∽△CBA.
∴=.∴CE·CB=CD·AC.
∵AC=AB=4,∴×2=4CD.
∴CD=.
5.(深圳中考)如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧形小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
解:∵=,DE=8,
解得EF=12.
∵EG=3,HF=1,
∴GH=EF-EG-HF=8.
由垂径定理,得GM=GH=4.
又MN=2,设半径OG=R,则OM=R-2.
在Rt△OMG中,由勾股定理,得
OM2+MG2=OG2.
∴(R-2)2+42=R2.解得R=5.
答:小桥所在圆的半径为5米.
6.(安徽中考)在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
解:(1)连接OQ.
∵PQ∥AB,PQ⊥OP,
∴OP⊥AB.
∵AB=6,∴OB=3.
∵∠ABC=30°,
tan∠ABC=,即=.
∴OP=.
由勾股定理,得
PQ===.
(2)连接OQ.
由勾股定理,得PQ==.
要使PQ取最大值,需OP取最小值,此时OP⊥BC.
∵∠ABC=30°,
∴OP=OB=,此时PQ最大==.
7.(烟台中考)如图,以△ABC的一边AB为直径的半圆与其他两边AC,BC的交点分别为D,E,且=.
(1)试判断△ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求sin∠ABD的值.
解:(1)△ABC为等腰三角形.理由如下:
连接AE,∵=,
∴∠DAE=∠BAE,
即AE平分∠BAC.
∵AB为直径,
∴∠AEB=∠AEC=90°,即AE⊥BC.
又∵AE=AE,
∴△CAE≌△BAE.∴AC=AB.
∴△ABC为等腰三角形.
(2)∵△ABC为等腰三角形,AE⊥BC,
∴BE=CE=BC=×12=6.
在Rt△ABE中,∵AB=10,BE=6,
∴AE==8.
∵AB为直径,∴∠ADB=90°.
∴S△ABC=AE·BC=BD·AC.
∴BD==.
在Rt△ABD中,∵AB=10,BD=,
∴AD==.
∴sin∠ABD===.
8.如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D为BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED,若存在,请求出PB的长;若不存在,请说明理由.
解:(1)证明:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°.
∵点D是BC的中点,
∴AD是线段BC的垂直平分线.
∴AB=AC.
∵AB=BC,∴AB=BC=AC.
∴△ABC为等边三角形.
(2)连接BE.
∵AB是直径,∴∠AEB=90°.
∴BE⊥AC.
∵△ABC是等边三角形,
∴AE=EC,即E为AC的中点.
∵D是BC的中点,故DE为△ABC的中位线,
∴BD=BC=1,DE=AB=×2=1.
(3)假设存在点P,使△PBD≌△AED.
∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°.
∴∠PBD=120°.
∵DE∥AB,∴∠AED=120°.
又∵△PBD≌△AED,BD=ED,
∴PB=AE=1.
周周练(3.1~3.4)
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.下列说法中,错误的是(B)
A.直径相等的两个圆是等圆
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.圆中最长的弦是直径
D.一条弦把圆分成两条弧,这两条弧可能是等弧
2.(娄底中考)如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为(C)
A.20°
B.40°
C.50°
D.70°
3.(泰安中考)如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于(D)
A.180°-2α
B.2α
C.90°+α
D.90°-α
4.如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是(B)
A.3≤OM≤5
B.4≤OM≤5
C.3<OM<5
D.4<OM<5
5.AB是⊙O的弦,OQ⊥AB,垂足为Q,再以OQ为半径作同心圆,称作小⊙O,点P是AB上异于A,B,Q的任意一点,则点P位置是(D)
A.在大⊙O上
B.在大⊙O外部
C.在小⊙O内部
D.在小⊙O外,大⊙O内
6.如图,△ABC内接于⊙O,∠C=30°,AB=2,则⊙O的半径为(B)
A.
B.2
C.2
D.4
7.已知⊙O的直径CD=10
cm,AB是⊙O的弦,AB=8
cm,且AB⊥CD,垂足为M,则AC的长为(C)
A.2
cm
B.4
cm
C.2
cm或4
cm
D.2
cm或4
cm
8.(泰安中考)如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE∶S△CDB的值等于(D)
A.1∶
B.1∶
C.1∶2
D.2∶3
二、填空题(每小题5分,共20分)
9.已知⊙O的直径为6,点M到圆心O的距离为4,则点M与⊙O的位置关系是点M在⊙O外.
10.如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于60度.
11.如图,AD和AC分别是⊙O的直径和弦,且∠CAD=30°,OB⊥AD,交AC于点B,若OB=3,则BC=3.
12.如图,点A,B,C,D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=60°.
三、解答题(共48分)
13.(10分)已知⊙O的半径为1,点P与圆心O的距离为d,且方程x2-2x+d=0有实数根,则点P与⊙O有怎样的位置关系?
解:∵方程x2-2x+d=0有实数根,
∴(-2)2-4×1×d=4-4d≥0.∴d≤1.
又∵d≥0,∴0≤d≤1.
∴当d=1时,点P在⊙O上;
当0≤d<1时,点P在⊙O内.
综上所述,点P在⊙O内或⊙O上.
14.(12分)如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一点(不与点A,B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)弦长AB等于2(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数.
解:连接OA.
∵OA=OB,OA=OD,
∴∠BAO=∠B,∠DAO=∠D.
∴∠DAB=∠BAO+∠DAO=∠B+∠D.
又∵∠B=30°,∠D=20°,
∴∠DAB=50°.
∴∠BOD=2∠DAB=100°.
15.(12分)已知⊙O的直径为10,点A,B,C在⊙O上,∠CAB的平分线交⊙O于点D.
图1 图2
(1)如图1,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图2,若∠CAB=60°,求BD的长.
解:(1)∵BC是⊙O的直径,
∴∠CAB=∠BDC=90°.
∵在Rt△CAB中,BC=10,AB=6,
∴AC===8.
∵AD平分∠CAB,∴=.∴CD=BD.
在Rt△BDC中,BC=10,CD2+BD2=BC2,
∴BD=CD=5.
(2)连接OB,OD.
∵AD平分∠CAB,且∠CAB=60°,
∴∠DAB=∠CAB=30°.
∴∠DOB=2∠DAB=60°.
又∵OB=OD,∴△OBD是等边三角形.
∴BD=OB=×10=5.
16.(14分)如图1所示,已知△ABC是等边三角形,以BC为直径作⊙O交AB,AC于D,E.
(1)求证:△ODE是等边三角形;
(2)如图2所示,若∠A=60°,AB≠AC,则(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
解:(1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°.
∵OB=OC=OD=OE,
∴△BOD,△COE是等边三角形.
∴∠BOD=∠COE=60°.∴∠DOE=60°.
∴△ODE是等边三角形.
(2)仍然成立.
证明:连接CD.
∵BC是⊙O的直径,
∴∠BDC=90°.∴∠ADC=90°.
∵∠A=60°,∴∠ACD=30°.
∴∠DOE=2∠ACD=60°.
∵OD=OE,
∴△ODE是等边三角形.
3.5 确定圆的条件
基础题
知识点1 确定圆的条件
1.下列条件,可以画出唯一一个圆的是(D)
A.已知圆心
B.已知半径
C.已知直径
D.已知不在同一条直线上的三个点
2.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是(B)
A.点P
B.点Q
C.点R
D.点M
3.在同一平面上有A,B,C三点,若经过A,B,C这三点画圆,则可画(C)
A.0个
B.1个
C.0个或1个
D.无数个
4.平面上有三个点A,B,C,若AB=5
cm,BC=3
cm,CA=4
cm,则过A,B,C三点可以(填“可以”或“不可以”)确定一个圆,且圆心在AB上,是AB的中点.
知识点2 三角形的外接圆
5.(株洲中考)如图,⊙O是△ABC的外接圆,∠A=68°,则∠OBC的大小是(A)
A.22°
B.26°
C.32°
D.68°
6.一个三角形的外心在其内部,则这个三角形是(C)
A.任意三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
7.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则以A,B,C为顶点的三角形外接圆的圆心坐标是(C)
A.(2,3)
B.(3,2)
C.(3,1)
D.(1,3)
8.点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为(C)
A.40°
B.100°
C.40°或140°
D.40°或100°
9.(扬州中考)如图,⊙O是△ABC的外接圆,直径AD=4,∠ABC=∠DAC,则AC的长为2.
10.如图,一只猫观察到一老鼠洞的三个洞口A,B,C,这三个洞口不在同一条直线上,请问这只猫应该在什么地方才能最省力同时顾及三个洞口?作出这个位置.
解:如图,连接AB,BC,分别作线段AB,BC的垂直平分线,且相交于点O,点O即为所求.
中档题
11.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是(B)
A.第①块
B.第②块
C.第③块
D.第④块
12.小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹);
(2)若△ABC中,AB=8米,AC=6米,∠BAC=90°,试求小明家圆形花坛的面积.
解:(1)用尺规作出AB,AC的垂直平分线,交于O点,以O为圆心,OA长为半径作出⊙O,⊙O即为花坛的位置,如图.
(2)∵∠BAC=90°,AB=8米,AC=6米,
∴BC=10米.
∴△ABC外接圆的半径为5米.
∴小明家圆形花坛的面积为25π平方米.
13.如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.
(1)当α=35°时,求β的度数;
(2)猜想α与β之间的关系,并给予证明.
解:(1)连接OB,则OA=OB.
∵∠OAB=35°,
∴∠OBA=∠OAB=35°.
∴∠AOB=180°-35°-35°=110°.
∴β=∠C=∠AOB=55°.
(2)α与β之间的关系是α+β=90°.
证明:∵∠OBA=∠OAB=α,
∴∠AOB=180°-2α.
∵β=∠C=∠AOB,
∴β=(180°-2α)=90°-α.
∴α+β=90°.
综合题
14.(福州中考)如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
(1)求BC的长;
(2)求⊙O的半径.
解:(1)作AE⊥BC,垂足为E.
在Rt△ABE中,
∵∠B=45°,AB=3,
∴AE=BE=3.
在Rt△ACE中,∵∠ACE=60°,AE=3,
∴CE===.
∴BC=BE+CE=3+.
(2)作直径AF,连接CF,则∠ACF=90°.
在Rt△ACE中,∵∠ACE=60°,AE=3,
∴AC===2.
∵∠F=∠D,∠D=∠ACB=60°,
∴∠F=60°.
在Rt△AFC中,∵sinF=,
∴AF===4.
∴⊙O半径OA=2.
3.6 直线和圆的位置关系
第1课时 直线和圆的位置关系及切线的性质
基础题
知识点1 直线和圆的位置关系
1.下图中直线l是⊙O的切线的图形是(C)
2.(梧州中考)已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为(C)
A.相离
B.相切
C.相交
D.无法确定
3.已知⊙O的面积为9π
cm2,若点O到直线l的距离为π
cm,则直线l与⊙O的位置关系是(C)
A.相交
B.相切
C.相离
D.无法确定
4.在平面直角坐标系xOy中,以点(-3,4)为圆心,4为半径的圆(C)
A.与x轴相交,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
5.已知⊙O的直径为6,圆心O到直线l的距离为d,(1)当直线l与⊙O相离时,d的取值范围是d>3;(2)当直线l与⊙O相切时,则d=3;
(3)当直线l与⊙O相交时,d的取值范围是d<3.
6.(湘西中考改编)如图,在Rt△ABC中,∠C=90°,BC=3
cm,AC=4
cm,以点C为圆心,以2.5
cm为半径画圆,则⊙C与直线AB有何种位置关系?请说明理由.
解:⊙O与直线AB相交.理由:
过C作CD⊥AB于D.
∵在Rt△ABC中,∠C=90°,BC=3
cm,AC=4
cm,
∴AB==5
cm.
∵S△ABC=AC·BC=AB·CD,
∴3×4=5CD.∴CD=2.4<2.5,即d<r.
∴⊙C与直线AB的位置关系是相交.
知识点2 切线的性质
7.如图,PA,PB是⊙O的切线,切点分别是A,B,如果∠P=60°,那么∠AOB等于(C)
A.60°
B.90°
C.120°
D.150°
8.(海南中考)如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.∠APO=40°,则∠ABC的度数为(B)
A.20°
B.25°
C.40°
D.50°
9.(赤峰中考)如图,两同心圆的大圆半径长为5
cm,小圆半径长为3
cm,大圆的弦AB与小圆相切,切点为C,则弦AB的长是8__cm.
10.(丽水中考改编)如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.求证:∠A=∠ADE.
证明:连接OD.
∵DE是切线,∴∠ODE=90°.
∴∠ADE+∠BDO=90°.
∵∠ACB=90°,
∴∠A+∠B=90°.
∵OD=OB,∴∠B=∠BDO.
∴∠A=∠ADE.
中档题
11.(湖州中考)如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作⊙O的切线,交AB的延长线于点D,则∠D的度数是(B)
A.25°
B.40°
C.50°
D.65°
12.(益阳中考)如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为(B)
A.1
B.1或5
C.3
D.5
13.(永州中考)如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m=1;
(2)当m=2时,d的取值范围是1<d<3.
14.(龙岩中考)如图,Rt△ABC中,∠C=90°,BC=3,点O在AB上,OB=2,以OB长为半径的⊙O与AC相切于点D,交BC于点F,OE⊥BC于点E,则弦BF的长为2.
15.(丹东中考)如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
解:(1)证明:连接OD.
∵CD是⊙O切线,
∴∠ODC=90°,
即∠ODB+∠BDC=90°.
∵AB为⊙O的直径,
∴∠ADB=90°,即∠ODB+∠ADO=90°.
∴∠BDC=∠ADO.
∵OA=OD,∴∠ADO=∠A.∴∠BDC=∠A.
(2)∵CE⊥AE,∴∠E=∠ADB=90°.∴DB∥EC.∴∠DCE=∠BDC.
∵∠BDC=∠A,∴∠A=∠DCE.
又∵∠E=∠E,∴△AEC∽△CED.
∴=,即EC2=DE·AE.
∴16=2(2+AD).∴AD=6.
综合题
16.(金华中考)如图,已知AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F,连接OC,AC.
(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数;
②若⊙O的半径为2,求线段EF的长.
解:(1)证明:∵CD是⊙O的切线,∴OC⊥CD.
∵AD⊥CD,∴AD∥OC.∴∠DAC=∠OCA.
∵OC=OA,
∴∠OCA=∠OAC.
∴∠OAC=∠DAC.∴AC平分∠DAO.
(2)①∵AD∥OC,∴∠EOC=∠DAO=105°.
∵∠E=30°,∴∠OCE=45°.
②作OG⊥CE于点G,则CG=FG.
∵OC=2,∠OCE=45°,∴CG=OG=2,FG=2.
在Rt△OGE中,∠E=30°,OG=2,∴GE=2.
∴EF=GE-FG=2-2.
第2课时 切线的判定与三角形的内切圆
基础题
知识点1 切线的判定
1.下列直线是圆的切线的是(B)
A.与圆有公共点的直线
B.圆心到直线的距离等于半径的直线
C.垂直于圆的半径的直线
D.过圆直径外端点的直线
2.如图,AB是⊙O的直径,下列条件中不能判定直线AT是⊙O的切线的是(D)
A.AB=4,AT=3,BT=5
B.∠B=45°,AB=AT
C.∠B=55°,∠TAC=55°
D.∠ATC=∠B
3.如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为∠ABC=90°或AB⊥BC.
4.如图,点A,B,D在⊙O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=40°,直线BC与⊙O的位置关系为相切.
5.(济宁中考改编)如图,已知⊙O的直径AB=12,弦AC=10,D是弧BC的中点,过点D作DE⊥AC,交AC的延长线于点E.求证:DE是⊙O的切线.
证明:连接OD.
∵D为弧BC的中点,
∴=.
∴∠BOD=∠BAE.
∴OD∥AE.
∵DE⊥AC,∴∠AED=90°.
∴∠ODE=90°.∴OD⊥DE.
∴DE为⊙O的切线.
知识点2 三角形的内切圆
6.有关三角形内心的说法正确的是(D)
A.内心是三边垂直平分线的交点
B.内心是三条中线的交点
C.内心到三个顶点的距离相等
D.内心到三边的距离相等
7.如图,在△ABC中,∠A=50°,内切圆I与边BC,CA,AB分别相切于点D,E,F,则∠EDF的度数为(C)
A.55°
B.60°
C.65°
D.70°
8.如图,在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆的半径是(B)
A.
B.1
C.2
D.
中档题
9.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是(C)
A.点(0,3)
B.点(2,3)
C.点(5,1)
D.点(6,1)
10.如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,OB长为半径作⊙O,要使射线BA与⊙O相切,应将射线绕点B按顺时针方向旋转(B)
A.40°或80°
B.50°或110°
C.50°或100°
D.60°或120°
11.(徐州中考)如图,⊙O是△ABC的内切圆,若∠ABC=70°,∠ACB=40°,则∠BOC=125°.
12.(南充中考)如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.
解:(1)证明:连接OD,CD.
∵AC为⊙O的直径,
∴△BCD是直角三角形.
∵E为BC的中点,
∴BE=CE=DE.∴∠CDE=∠DCE.
∵OD=OC,∴∠ODC=∠OCD.
∵∠ACB=90°,∴∠OCD+∠DCE=90°.
∴∠ODC+∠CDE=90°,即OD⊥DE.
∴DE是⊙O的切线.
(2)设⊙O的半径为r,∵∠ODF=90°,
∴OD2+DF2=OF2,即r2+42=(r+2)2.解得r=3.
∴⊙O的直径为6.
13.(呼伦贝尔中考)如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得
ED=EA.
(1)求证:ED是⊙O的切线;
(2)当OE=10时,求BC的长.
解:(1)证明:连接OD.∵AC⊥AB,
∴∠BAC=90°,
即∠OAE=90°.
在△AOE和△DOE中,
∴△AOE≌△DOE(SSS).
∴∠OAE=∠ODE=90°,即OD⊥ED.
又∵OD是⊙O的半径,∴ED是⊙O的切线.
(2)∵AB是直径.
∴∠ADB=90°,即AD⊥BC.
又∵由(1)知,△AOE≌△DOE,
∴∠AEO=∠DEO.
又∵AE=DE,∴OE⊥AD.
∴OE∥BC.∴△AOE∽△ABC.
∴==.
∴BC=2OE=20,即BC的长是20.
综合题
14.(常德中考)已知,如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长.
解:(1)证明:连接FO,
∵点O为AC的中点,点F为BC的中点,
∴OF∥AB.
∵AC为⊙O的直径,
∴CE⊥AE.
∵OF∥AB,∴OF⊥CE.
∴OF所在直线垂直平分CE.
∴FC=FE,OE=OC.
∴∠FEC=∠FCE,∠OEC=∠OCE.
∵∠ACB=90°,
∴∠OCE+∠FCE=90°.
∴∠OEC+∠FEC=90°,即∠FEO=90°.
∵点E在⊙O上,
∴FE为⊙O的切线.
(2)∵⊙O的半径为3,∴AO=CO=EO=3.
∵∠EAC=60°,OA=OE,∴∠EOA=60°,
∴∠COD=∠EOA=60°.
∵在Rt△OCD中,∠COD=60°,OC=3,
∴CD=3.
∵在Rt△ACD中,∠ACD=90°,CD=3,AC=6,
∴AD=3.
小专题(九) 证明圆的切线的两种方法
方法1 连半径、证垂直
要证明某直线是圆的切线,当直线与圆有公共点时,可连接圆心与公共点,证明连线与直线垂直即可证得直线是圆的切线.
【例1】 (黄石中考)如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
解:(1)∵AB是⊙O的直径,C在⊙O上,∴∠ACB=90°.
又∵BC=3,AB=5,
∴AC=4.
(2)证明:连接OC.
∵AC是∠DAB的平分线,
∴∠DAC=∠BAC.
又∵AD⊥DC,∴∠ADC=∠ACB=90°.
∴∠DCA=∠B.
又∵OA=OC,∴∠OAC=∠OCA.
∵∠OAC+∠B=90°,
∴∠OCA+∠ACD=∠OCD=90°,即OC⊥CD.
∴DC是⊙O的切线.
INCLUDEPICTURE
"../../../针对训练.TIF"
\
MERGEFORMAT
1.(本溪中考)如图,△ABC中,AB=AC,点E是线段BC延长线上一点,ED⊥AB,垂足为D,ED交线段AC于点F,点O在线段EF上,⊙O经过C,E两点,交ED于点G.
(1)求证:AC是⊙O的切线;
(2)若∠E=30°,AD=1,BD=5,求⊙O的半径.
解:(1)证明:连接CO.
∵AB=AC,
∴∠B=∠ACB.
∵OC=OE,
∴∠OCE=∠E.
∵DE⊥AB,
∴∠BDE=90°.
∴∠B+∠E=90°.∴∠ACB+∠OCE=90°.
∴∠ACO=90°,即AC⊥OC.
∴AC是⊙O的切线.
(2)∵∠E=30°,∴∠OCE=30°.∴∠FCE=120°.
∴∠CFO=30°.∴∠AFD=∠CFO=30°.
∴DF=AD=.
∵BD=5,∴DE=5.
∵OF=2OC,∴EF=3OE=4.
∴OE=,即⊙O的半径为.
2.(枣庄中考)如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB,AB,∠PBA=∠C.
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2,求BC的长.
解:(1)证明:连接OB.
∵AC是⊙O的直径,
∴∠ABC=90°.
∴∠C+∠BAC=90°.
∵OA=OB,
∴∠BAC=∠OBA.
∵∠PBA=∠C,
∴∠PBA+∠OBA=90°,即PB⊥OB.
∴PB是⊙O的切线.
(2)∵⊙O的半径为2,∴OB=2,AC=4.
∵OP∥BC,∴∠BOP=∠OBC=∠C.
又∵∠ABC=∠PBO=90°,∴△ABC∽△PBO.
∴=,即=.∴BC=2.
3.(广安中考)如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=,求⊙O的半径r及sinB.
解:(1)证明:连接OA,OD.
∵点D为CE的下半圆弧的中点,
∴OD⊥BC.
∴∠EOD=90°.
∵AB=BF,OA=OD,
∴∠BAF=∠BFA,∠OAD=∠D.
又∵∠BFA=∠OFD,
∴∠OAD+∠BAF=∠D+∠DFO=90°,
即∠OAB=90°.
∴OA⊥AB.∴AB是⊙O切线.
(2)OF=CF-OC=4-r,OD=r,DF=,
在Rt△DOF中,OD2+OF2=DF2,
即r2+(4-r)2=()2.解得r1=3,r2=1(舍去).
∴OA=3,OF=CF-OC=4-3=1,BO=BF+FO=AB+1.
在Rt△AOB中,AB2+OA2=OB2,
∴AB2+32=(AB+1)2.∴AB=4,OB=5.
∴sinB==.
方法2 作垂直,证半径
当条件中没有指出圆与直线有公共点时,可先过圆心作直线的垂线,再证明垂线段的长和半径相等即可证得直线是圆的切线.
【例2】 (南充中考)如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,OC=1,以点O为圆心,OC为半径作半圆.
(1)求证:AB为⊙O的切线;
(2)如果tan∠CAO=,求cosB的值.
解:(1)证明:作OM⊥AB于M,
∵OA平分∠CAB,OC⊥AC,OM⊥AB,
∴OC=OM.
∴AB是⊙O的切线.
(2)设BM=x,
OB=y,则y2-x2=1,①
∵tan∠CAO=,OC=1,∴AC=AM=3.
∵cosB==,∴=.
∴x2+3x=y2+y.②
由①②可得y=3x-1,∴(3x-1)2-x2=1.
∴x=,y=.∴cosB==.
INCLUDEPICTURE
"../../../针对训练.TIF"
\
MERGEFORMAT
4.如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3.
(1)求证:AC是⊙D的切线;
(2)求线段AC的长.
解:(1)证明:过点D作DF⊥AC于F.
∵AB为⊙D的切线,
∴∠B=90°.
∴AB⊥BC.
∵AD平分∠BAC,DF⊥AC,
∴BD=DF.
∴AC与⊙D相切.
(2)∵BD=DF,DE=DC,
∴Rt△BDE≌Rt△FDC(HL).∴EB=FC.
∵AB=AF,
∴AC=AF+FC=AB+EB=5+3=8.
5.如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M,与AB,AD分别相交于点E,F.求证:CD与⊙O相切.
证明:连接OM,过点O作ON⊥CD,垂足为N.
∵⊙O与BC相切于M,
∴OM⊥BC.
∵在正方形ABCD中,AC平分∠BCD,
又∵ON⊥CD,OM⊥BC,
∴OM=ON.
∴N在⊙O上.
∴CD与⊙O相切.
6.如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.
解:(1)证明:连接OC,作OD⊥PB于D点.
∵⊙O与PA相切于点C,∴OC⊥PA.
∵点O在∠APB的平分线上,OC⊥PA,OD⊥PB,
∴OD=OC.∴直线PB与⊙O相切.
(2)设PO交⊙O于F,连接CF.
∵OC=3,PC=4,∴PO=5,PE=8.
∵⊙O与PA相切于点C,∴∠PCF=∠E.
又∵∠CPF=∠EPC,∴△PCF∽△PEC.
∴CF∶CE=PC∶PE=4∶8=1∶2.
∵EF是直径,∴∠ECF=90°.
设CF=x,则EC=2x.则x2+(2x)2=62.
解得x=.
∴EC=2x=.
3.7 切线长定理
基础题
知识点 切线长定理
1.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是(B)
A.4
B.8
C.4
D.8
2.如图,△MBC中,∠B=90°,∠C=60°,MB=2,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为(C)
A.
B.
C.2
D.3
3.如图,PA,PB是⊙O的切线,切点为A,B,若OP=4,PA=2,则∠AOB的度数为(C)
A.60°
B.90°
C.120°
D.无法确定
4.如图,P为⊙O外一点,PA,PB分别切⊙O于点A,B,CD切⊙O于点E且分别交PA,PB于点C,D,若PA=4,则△PCD的周长为(C)
A.5
B.7
C.8
D.10
5.一个钢管放在V形架内,如图是其截面图,O为钢管的圆心.如果钢管的半径为25
cm,∠MPN=60°,则OP=(A)
A.50
cm
B.25
cm
C.
cm
D.50
cm
6.如图,AB为⊙O的直径,点C在AB的延长线上,CD,CE分别与⊙O相切于点D,E,若AD=2,∠DAC=∠DCA,则CE=2.
7.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,分别交PA,PB于C,D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是.
8.如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠P=60°,OA=2,求BC的长.
解:∵PA,PB是⊙O的切线,∴AP=BP.
又∵∠P=60°,
∴∠PAB=60°.
∵PA是⊙O的切线,
∴∠PAC=90°.
∴∠BAC=90°-60°=30°.
又∵AC是⊙O的直径,
∴∠ABC=90°.
∴BC=AC=OA=2.
9.在一个夹角为120°的墙角放置了一个圆柱体的容器,俯视图如图,在俯视图中圆与两边的墙分别切于B,C两点.(圆柱体容器的直径不易直接测量)
(1)写出此图中相等的线段;
(2)请你设计一种可以通过计算求出直径的测量方法.(写出主要解题过程)
解:(1)根据切线长定理,知AB=AC.
(2)连接OB,OA.
∵∠BAC=120°,∴∠OAB=60°.
在Rt△AOB中,
OB=AB·tan∠OAB=AB.
∴圆的直径为2AB.
即只需测得AB的长,就可求得圆的直径.
中档题
10.如图,一圆内切于四边形ABCD,AB=16,CD=10,则四边形的周长为(B)
A.50
B.52
C.54
D.56
11.如图,△ABC是一张周长为17
cm的三角形纸片,BC=5
cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为(B)
A.12
cm
B.7
cm
C.6
cm
D.随直线MN的变化而变化
12.如图,P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B,C是弧AB上的任意一点,过点C的切线分别交PA、PB于点D、E.
(1)若PA=4,求△PED的周长;
(2)若∠P=40°,求∠AFB的度数.
解:(1)∵DA,DC都是⊙O的切线,∴DC=DA,同理EC=EB.
∵P是⊙O外的一点,PA,PB分别与⊙O相切于点A、B,∴PA=PB.
∴△PED的周长为PD+PE+DE=PD+DC+PE+CE=PA+PB=2PA=8.
即△PDE的周长是8.
(2)连接AB,
∵PA=PB,∴∠PAB=∠PBA.
∵∠P=40°,
∴∠PAB=∠PBA=×(180°-40°)=70°.
∵BF⊥PB,BF为圆的直径,
∴∠ABF=90°-70°=20°,∠FAB=90°.
∴∠AFB=90°-20°=70°.
13.如图,PA,PB分别切⊙O于A,B,连接PO,与AB相交于D,C是⊙O上一点,∠C=60°.
(1)求∠APB的大小;
(2)若PO=20
cm,求△AOB的面积.
解:(1)∵∠C=60°,∴∠AOB=120°.
∵PA,PB分别切⊙O于A,B,
∴∠PAO=∠PBO=90°.
∴∠APB=60°.
(2)∵PA,PB分别切⊙O于A,B,
∴PA=PB.
∴点P在AB的垂直平分线上.
同理,点O在AB的垂直平分线上.
∴PO垂直平分AB.
∵∠APB=60°,∠AOB=120°,
∴∠OPB=∠OPA=30°,∠POB=∠POA=60°.
∵PO=20
cm,∴OB=10
cm.
∴OD=OB·cos∠POB=5
cm.
BD=OB·sin∠POB=5
cm.
∴AB=2BD=10
cm.
∴S△AOB=×10×5=25(cm2).
综合题
14.(贺州中考)如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6
cm,CO=8
cm.
(1)求证:BO⊥CO;
(2)求BE和CG的长.
解:(1)证明:∵AB∥CD,
∴∠ABC+∠BCD=180°.
∵AB,BC,CD分别与⊙O相切于E,F,G,
∴BO平分∠ABC,CO平分∠DCB.
∴∠OBC=∠ABC,∠OCB=∠DCB.
∴∠OBC+∠OCB=(∠ABC+∠DCB)=×180°=90°.
∴∠BOC=90°,∴BO⊥CO.
(2)连接OF,则OF⊥BC,
∵在Rt△BOC中,BO=6
cm,CO=8
cm,
∴BC==10(cm).
易证Rt△BOF∽Rt△BCO.∴=.
∴=,∴BF=3.6
cm.
∵AB,BC,CD分别与⊙O相切,
∴BE=BF=3.6
cm,CG=CF.
∵CF=BC-BF=10-3.6=6.4(cm),
∴CG=CF=6.4
cm.
小专题(十) 圆的切线的性质与判定的综合运用
1.(贵港中考)如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=,AB=12,求半圆O所在圆的半径.
解:(1)证明:连接OD,OA,作OE⊥AB于E,
∵AB=AC,O为BC的中点,
∴∠CAO=∠BAO.
∵OD⊥AC,OE⊥AB,∴OD=OE.
∵AB经过圆O半径的外端,
∴AB是半圆O所在圆的切线.
(2)由cos∠ABC=,AB=12,得OB=8.
由勾股定理,得AO==4.
∵S△AOB=AB·OE=OB·AO,
∴OE==,即半圆O所在圆的半径是.
2.如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
证明:(1)连接OD,BD.
∵AB是⊙O的切线,
∴AB⊥BC,即∠ABC=90°.
∵AB=AD,∴∠ABD=∠ADB.
∵OB=OD,∴∠DBO=∠BDO.
∴∠ABD+∠DBO=∠ADB+∠BDO.
∴∠ADO=∠ABO=90°.
∴AD是半圆O的切线.
(2)连接CD,求证:∠A=2∠CDE.
证明:由(1)知,∠ADO=∠ABO=90°,
∴∠A=360°-∠ADO-∠ABO-∠BOD=180°-∠BOD=∠DOC.
∵AD是半圆O的切线,∴∠ODE=90°.
∴∠ODC+∠CDE=90°.
∵BC是⊙O的直径,∴∠ODC+∠BDO=90°.
∴∠BDO=∠CDE.
∵∠BDO=∠OBD,∠DOC=2∠OBD,
∴∠DOC=2∠BDO.
∴∠DOC=2∠CDE.
∴∠A=2∠CDE.
3.(玉林中考)如图,AB是⊙O的直径,点C,D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA延长线与OC延长线于点E,F,连接BF.
(1)求证:BF是⊙O的切线;
(2)已知圆的半径为1,求EF的长.
解:(1)证明:连接OD,
∵四边形AOCD是平行四边形,OA=OC,
∴四边形AOCD是菱形.
∴△OAD和△OCD都是等边三角形.
∴∠AOD=∠COD=60°.∴∠FOB=60°.
∵EF为切线,∴OD⊥EF.∴∠FDO=90°.
在△FDO和△FBO中,
∴△FDO≌△FBO.∴∠ODF=∠OBF=90°.
∴OB⊥BF.∴BF是⊙O的切线.
(2)在Rt△OBF中,
∵∠FOB=60°,tan∠FOB=,
∴∠E=30°,BF=1×tan60°=.
∵∠E=30°,
∴EF=2BF=2.
4.(西宁中考)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,=,求BE的长.
解:(1)证明:连接OD,∵OB=OD,
∴∠OBD=∠BDO.
∵∠CDA=∠CBD,∴∠CDA=∠ODB.又∵AB是⊙O的直径,∴∠ADB=90°.
∴∠ADO+∠ODB=90°.
∴∠ADO+∠CDA=90°,即∠CDO=90°.
∴OD⊥CD.
∵OD是⊙O半径,∴CD是⊙O的切线.
(2)∵∠C=∠C,∠CDA=∠CBD,
∴△CDA∽△CBD.∴=.
∵=,BC=6,∴CD=4.
∵CE,BE是⊙O的切线,∴BE=DE,BE⊥BC.
∴BE2+BC2=EC2,即BE2+62=(4+BE)2.
解得BE=.
5.已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F,连接DF.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
解:(1)证明:连接OE,
则OB=OE.
∵△ABC是等边三角形,
∴∠ABC=∠C=60°.
∴△OBE是等边三角形.
∴∠OEB=∠C=60°.∴OE∥AC.
∵EF⊥AC,∴∠EFC=90°.
∴∠OEF=∠EFC=90°.∴EF是⊙O的切线.
(2)∵DF是⊙O的切线,∴∠ADF=90°.
设⊙O的半径为r,则BE=r,EC=4-r,
AD=4-2r.
在Rt△ADF中,∵∠A=60°,
∴AF=2AD=8-4r.
∴FC=4-(8-4r)=4r-4.
在Rt△CEF中,∵∠C=60°,
∴EC=2FC.∴4-r=2(4r-4),解得r=.
∴⊙O的半径是.
6.如图,AB是⊙O的直径,点P在⊙O上,且PA=PB,点M是⊙O外一点,MB与⊙O相切于点B,连接OM,过点A作AC∥OM交⊙O于点C,连接BC交OM于点D.
(1)求证:OD=AC;
(2)求证:MC是⊙O的切线;
(3)若MD=8,BC=12,连接PC,求PC的长.
解:(1)证明:∵AC∥OM,
∴△BOD∽△BAC.
∴
==
.
∴OD=AC.
(2)证明:连接OC,∵AC∥OM,
∴∠OAC=∠BOM,∠ACO=∠COM.
∵OA=OC,∴∠OAC=∠ACO.
∴∠BOM=∠COM.
在△OCM和△OBM中,
∴△OCM≌△OBM.
又∵MB是⊙O的切线,∴∠OCM=∠OBM=90°.
∴MC是⊙O的切线.
(3)∵AB是⊙O的直径,∴∠ACB=∠APB=90°,∵AC∥OM,∴OD⊥BC.
∴CD=BD=BC=6.
∴∠OCD+∠MCD=∠CMD+∠MCD=90°,
∴∠OCD=∠CMD.
∵∠OCM=∠CDO=∠CDM=90°,
∴△CDO∽△MDC.
∴CD2=OD·DM.∴OD=.∴OC=.
∴AB=15.∴PA=PB=,AC=9.
过点A作AH⊥PC于点H,∴AH=CH=.
∴PH==6.
∴PC=PH+CH=.
3.8 圆内接正多边形
基础题
知识点1 圆内接正多边形的概念
1.下列说法错误的是(C)
A.圆内接正多边形每个内角都相等
B.圆内接正多边形都是轴对称图形
C.圆内接正多边形都是中心对称图形
D.圆内接正多边形的中心到各边的距离相等
知识点2 圆内接正多边形的有关计算
2.中心角为30°的圆内接正n边形的n等于(B)
A.10
B.12
C.14
D.15
3.(青岛中考)如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=(A)
A.30°
B.35°
C.45°
D.60°
4.如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB等于(B)
A.30°
B.45°
C.55°
D.60°
5.(滨州中考)若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为(B)
A.6,3
B.3,3
C.6,3
D.6,3
6.(西宁中考)一元钱硬币的直径约为24
mm,则用它能完全覆盖住的正六边形的边长最大不能超过(A)
A.12
mm
B.12
mm
C.6
mm
D.6
mm
7.如图,点O是正五边形ABCDE的中心,则∠BAO的度数为54°.
8.(盐城中考)如图,正六边形ABCDEF内接于半径为4的圆,则B,E两点间的距离为8.
9.已知正六边形的边心距为,求正六边形的中心角、边长、周长和面积.
解:如图,连接OB,OC,过点O作OH⊥BC于H,
∵六边形ABCDEF是正六边形,∴∠BOC=×360°=60°.
∵OB=OC,∴△OBC是等边三角形.
∴∠OBC=60°,BC=OB=OC.
∵OH=,∴sin∠OBC===.
∴OB=BC=2.
∴正六边形的周长为2×6=12.
∴S正六边形ABCDEF=6S△OBC=6××2×=6.
∴正六边形的中心角为60°,边长为2,周长为12,面积为6.
知识点3 圆内接正多边形的作图
10.(兰州中考)如图,已知⊙O,用尺规作⊙O的内接正四边形ABCD.(写出结论,不写作法,保留作图痕迹)
解:画圆的一条直径AC,作这条直径的中垂线交⊙O于点B,D,连接AB,BC,CD,DA,得到圆内接正四边形ABCD.如图所示,四边形ABCD即为所求.
中档题
11.(泸州中考)以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是(D)
A.
B.
C.
D.
12.如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是(C)
A.5
B.6
C.7
D.8
13.(滨州中考)若正方形的外接圆半径为2,则其内切圆半径为(A)
A.
B.2
C.
D.1
14.(莱芜中考)正多边形的内切圆与外接圆的周长之比为∶2,则这个正多边形为(B)
A.正十二边形
B.正六边形
C.正四边形
D.正三角形
15.如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若A点的坐标为(-1,0),则点C的坐标为(,-).
16.(威海中考)如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为2.
17.如图,已知等边△ABC内接于⊙O,BD为⊙O内接正十二边形的一边,CD=5
cm,求⊙O的半径R.
解:连接OB,OC,OD,
∵等边△ABC内接于⊙O,BD为⊙O内接正十二边形的一边,
∴∠BOC=×360°=120°,∠BOD=×360°=30°.
∴∠COD=∠BOC-∠BOD=90°.
∵OC=OD,∴∠OCD=45°.
∴OC=CD·cos45°=5×=5(cm).
∴⊙O的半径R=5
cm.
综合题
18.如图1,2,3,…,m中,点M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEF…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是90°,图3中∠MON的度数是72°;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
解:(1)连接OA,OB.
∵正三角形ABC内接于⊙O,
∴AB=BC,∠OAM=∠OBN=30°,
∠AOB=120°.
∵BM=CN,∴AM=BN.
∴△AOM≌△BON(SAS).
∴∠AOM=∠BON.
∴∠AOM+∠BOM=∠BON+∠BOM.
∴∠AOB=∠MON=120°.
(3)∠MON=.
3.9 弧长及扇形的面积
基础题
知识点1 弧长公式及其应用(l=)
1.(云南中考)已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为(C)
A.
B.2π
C.3π
D.12π
2.(自贡中考)一个扇形的半径为8
cm,弧长为π
cm,则扇形的圆心角为(B)
A.60°
B.120°
C.150°
D.180°
3.(包头中考)120°的圆心角对的弧长是6π,则此弧所在圆的半径是(C)
A.3
B.4
C.9
D.18
4.(长春中考)如图,PA,PB是⊙O的切线,切点分别为A,B,若OA=2,∠P=60°,则的长为(C)
A.π
B.π
C.π
D.π
5.(莆田中考)如图,CD为⊙O的弦,直径AB为4,AB⊥CD于点E,∠A=30°,则的长为π(结果保留π).
6.一段圆弧形公路弯道,圆弧的半径为2
km,弯道所对圆心角为10°,一辆汽车从此弯道上驶过,用时20
s,弯道有一块限速警示牌,限速为40
km/h,问这辆汽车经过弯道时有没有超速?(π取3)
解:l==
km.
∴汽车的速度为÷=60(km/h).
∵60
km/h>40
km/h,
∴这辆汽车经过弯道时超速.
知识点2 扇形面积公式及其应用(S==lR)
7.(新疆中考)一个扇形的圆心角是120°,面积为3π
cm2,那么这个扇形的半径是(B)
A.1
cm
B.3
cm
C.6
cm
D.9
cm
8.(资阳中考)钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是(A)
A.π
B.π
C.π
D.π
9.(青岛中考)如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,长为25
cm,贴纸部分的宽BD为15
cm,若纸扇两面贴纸,则贴纸的面积为(B)
A.175π
cm2
B.350π
cm2
C.π
cm2
D.150π
cm2
10.(邵阳中考)如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是π.
11.(河北中考)如图,将长为8
cm的铁丝首尾相接围成半径为2
cm的扇形,则S扇形=4cm2.
中档题
12.(南充中考)如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是(A)
A.π
B.13π
C.25π
D.25
13.(莱芜中考)如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为(B)
A.π
B.2π
C.
D.4π
14.(天水中考)如图,△ABC是等边三角形,曲线CDEF叫做等边三角形的渐开线,其中,,的圆心依次是A,B,C,如果AB=1,那么曲线CDEF的长是4π.
15.(绥化中考)如图,在半径AC为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则图中阴影部分的面积是π-1.
16.(河南中考)如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作交于点C,若OA=2,则阴影部分的面积为-π.
17.(苏州中考改编)如图,在△ABC中,AB=AC.分别以B,C为圆心,BC长为半径在BC下方画弧,设两弧交于点D,与AB,AC的延长线分别交于点E,F,连接AD,BD,CD.若BC=6,∠BAC=50°,求,的长度之和(结果保留π).
解:∵AB=AC,∠BAC=50°,
∴∠ABC=∠ACB=65°.
∵BD=CD=BC,
∴△BDC为等边三角形.
∴∠DBC=∠DCB=60°.
∴∠DBE=∠DCF=55°.
∵BC=6,∴BD=CD=6.
∴l=l==.
∴、的长度之和为+=.
综合题
18.如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,经过点C,求图中阴影部分的面积.
解:令OF交BC于点G,OE交AC于点H,
作OM⊥BC于点M,ON⊥AC于点N.
∵CA=CB,∠ACB=90°,点O为AB的中点,
∴OC=AB=1,四边形OMCN是正方形.
∴OM=ON=.
∴S扇形FOE==.
∵∠GOH=∠MON=90°,∴∠GOM=∠HON.
在△OMG和△ONH中,
∴△OMG≌△ONH(ASA).
∴S四边形OGCH=S正方形OMCN=OM2=()2=.
∴S阴影=-.
小专题(十一) 教材P101随堂练习T1的变式与应用
——和阴影部分面积有关的计算
教材母题:如图,水平放置的一个油管的横截面半径为12
cm,其中有油的部分油面高6
cm,求截面上有油部分的面积(结果精确到0.1
cm2).
【解答】 连接AO,BO,过点O作OC⊥AB于点C.
由题意可知OC=12-6=6(cm),OA=12
cm.
∴sin∠OAC==.
∴∠OAC=30°,AC=6
cm.
∴∠AOC=60°,AB=12
cm.
∴∠AOB=120°.∴S扇形AOB=×π×122=48π(cm2),
S△AOB=AB·OC=×12×6=36(cm2).
∴
S=S扇形AOB-S△AOB=48π-36≈88.4(cm2).
∴截面上有油部分的面积约为88.4
cm2.
【方法归纳】 求阴影部分的面积有以下几种方法:
①直接用公式法;②和差法:计算某部分的面积,可以把这部分看作几部分的和或差,再分别利用公式计算,从而求得阴影部分的面积;③割补法:通过割或补,把不规则图形的面积转化为规则图形的面积;④等积变形法:先利用平移、旋转、对称等全等变换,将不规则图形的面积转化为一个和它面积相等的规则图形的面积,再利用公式计算.
INCLUDEPICTURE
"../../../针对训练.TIF"
\
MERGEFORMAT
1.(重庆中考)如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=,则图中阴影部分的面积是(A)
A.
B.+
C.
D.+
2.(枣庄中考)如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则阴影部分的面积为(D)
A.2π
B.π
C.
D.
3.(资阳中考)如图,在Rt△ABC中,∠ACB=90°,AC=2,以点B为圆心,BC的长为半径作弧,交AB于点D,若点D为AB的中点,则阴影部分的面积是(A)
A.2-π
B.4-π
C.2-π
D.π
4.(内江中考)如图,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为(C)
A.π-4
B.π-1
C.π-2
D.-2
5.如图,在矩形ABCD中,CD=1,∠DBC=30°.若将BD绕点B旋转后,点D落在DC延长线上的点E处,点D经过的路径,则图中阴影部分的面积是(B)
A.-
B.-
C.-
D.-
6.如图,三个小正方形的边长都为1,则图中阴影部分面积的和是(B)
A.
B.
C.
D.
7.如图,半径为2
cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为(A)
A.(-1)cm2
B.(+1)cm2
C.1
cm2
D.
cm2
8.(襄阳中考)如图,AB是半圆O的直径,点C,D是半圆O的三等分点,若弦CD=2,则图中阴影部分的面积为π.
9.(遵义中考)如图,在圆心角为90°的扇形OAB中,半径OA=2
cm,C为的中点,D,E分别是OA,OB的中点,则图中阴影部分的面积为(π+-)cm2.
10.(淮安中考)如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF.
(1)直接写出点F的坐标;
(2)求线段OB的长及图中阴影部分的面积.
解:(1)F(-2,0).
(2)连接AC交OB于点M.
∵四边形OABC为菱形,∴OC=OA,AC⊥OB.
∵OA=2,∠COA=60°,
∴△AOC为等边三角形.
∴AC=2,OM=,OB=2.
∴S阴影=S扇形OEB-2S△BOC=-2××2×1=4π-2.
11.(钦州中考)如图,点B,C,D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.
(1)求证:AC是⊙O的切线;
(2)求弦BD的长;
(3)求图中阴影部分的面积.
解:(1)证明:连接OC,交BD于点E.
∵∠CDB=30°,
∴∠BOC=60°.
∵∠OBD=30°,
∴∠OEB=90°.
∵AC∥BD,∴AC⊥OC.
∴AC是⊙O的切线.
(2)在Rt△OBE中,OB=6,∠OBD=30°,
∴OE=OB=3.
∴BE=3.∴BD=2BE=6.
(3)∵OE=EC=3,BE=ED,∠OEB=∠CED=90°,
∴△OBE≌△CDE(SAS).∴S△OBE=S△DEC.
∴S阴影=S扇形OBC==6π.
12.(襄阳中考)如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连接EF,CG.
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的,与线段CG所围成的阴影部分的面积.
解:(1)证明:∵四边形ABCD是正方形,
∴AB=BC=AD=2,
∠ABC=90°.
∵△BEC绕点B逆时针旋转90°得△BFA,
∴△ABF≌△CBE.
∴∠FAB=∠ECB,∠ABF=∠CBE=90°,AF=CE.
∴∠AFB+∠FAB=90°.
∵线段AF绕点F顺时针旋转90°得线段FG,
∴∠AFB+∠CFG=∠AFG=90°,AF=FG.
∴∠CFG=∠FAB=∠ECB.∴EC∥FG.
∵AF=EC,AF=FG,∴EC=FG.
∴四边形EFGC是平行四边形.∴EF∥CG.
(2)∵△ABF≌△CBE,∴FB=BE=AB=1.
∴AF==.
在△FEC和△CGF中,∵EC=GF,∠ECF=∠CFG,FC=CF,∴△FEC≌△CGF.
∴S△FEC=S△CGF.
∴S阴影=S扇形BAC+S△ABF+S△FGC-S扇形FAG
=+×2×1+×(1+2)×1-
=-.
章末复习(三) 圆
基础题
知识点1 圆的有关概念
1.下列命题中正确的有(A)
①弦是圆上任意两点之间的部分;②半径是弦;③直径是最长的弦;④弧是半圆,半圆是弧.
A.1个
B.2个
C.3个
D.4个
2.如图,在△ABC中,∠ACB=90°,∠A=40°,以点C为圆心,CB为半径的圆交AB于点D,连接CD,则∠ACD=(A)
A.10°
B.15°
C.20°
D.25°
知识点2 圆的对称性
3.下列四个图形中,既是轴对称图形,又是中心对称图形的是(C)
A.等边三角形
B.平行四边形
C.圆
D.正五边形
4.如图,AB是⊙O的直径,点C在⊙O上,∠AOC=40°,D是的中点,则∠ACD=125°.
知识点3 垂径定理
5.如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合),连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=(B)
A.4
B.5
C.5.5
D.6
6.(六盘水中考)赵州桥是我国建筑史上的一大创举,它距今约1
400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R=25米.
知识点4 圆周角定理及其推论
7.如图,已知A,B均为⊙O上一点,若∠AOB=80°,则∠ACB=(D)
A.80°
B.70°
C.60°
D.40°
8.如图是一个圆形人工湖的平面图,弦AB是湖上的一座桥,已知桥长100
m,测得圆周角∠ACB=30°,则这个人工湖的直径为200m.
9.如图,∠DAE是⊙O的内接四边形ABCD的一个外角,且∠DAE=∠DAC.求证:DB=DC.
证明:∵∠DAE是⊙O的内接四边形ABCD的一个外角,
∴∠DAE=∠DCB.
又∵∠DAE=∠DAC,
∴∠DCB=∠DAC.
又∵∠DAC=∠DBC,
∴∠DCB=∠DBC.
∴DB=DC.
知识点5 三角形的外接圆与内切圆
10.如图,点O是△ABC的内心,∠A=62°,则∠BOC等于(D)
A.59°
B.31°
C.124°
D.121°
11.如图,已知等腰△ABC.
(1)用直尺和圆规作△ABC的外接圆;
(2)设△ABC的外接圆的圆心为点O,若∠BOC=128°,求∠BAC的度数.
解:(1)如图.
(2)在优弧BC上任取一点D,连接BD,CD.
∵∠BOC=128°,
∴∠BDC=∠BOC=64°.
∴∠BAC=180°-∠BDC=116°.
知识点6 点、直线与圆的位置关系
12.(白银中考)已知⊙O的半径是6
cm,点O到同一平面内直线l的距离为5
cm,则直线l与⊙O的位置关系是(A)
A.相交
B.相切
C.相离
D.无法判断
13.如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的值可以是下列选项中的(B)
A.3
B.4
C.5
D.6
知识点7 切线的性质与判定
14.(益阳中考)如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为115°.
15.如图,直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为2.
16.(宿迁中考)如图1,在△ABC中,点D在边BC上,∠B∶∠C∶∠ADB=1∶2∶3,⊙O是△ABD的外接圆.
图1
图2
(1)求证:AC是⊙O的切线;
(2)当BD是⊙O的直径时(如图2),求∠CAD的度数.
解:(1)证明:连接AO,延长AO交⊙O于点E,则AE为⊙O的直径,连接DE.
∵∠B∶∠C∶∠ADB=1∶2∶3,∠ADB=∠C+∠CAD,∴∠B=∠CAD.
∵AE为⊙O的直径,∴∠ADE=90°.
∴∠EAD=90°-∠E.
∵∠E=∠B,∴∠E=∠B=∠CAD.
∴∠EAD+∠CAD=90°,即∠EAD+∠CAD=90°.
∴EA⊥AC,∴AC是⊙O的切线.
(2)∵BD是⊙O的直径,
∴∠BAD=90°.∴∠B+∠ADB=90°.
∵∠B∶∠C∶∠ADB=1∶2∶3,
∴4∠B=90°.∴∠B=22.5°.
由(1)知∠ABC=∠CAD,∴∠CAD=22.5°.
知识点8 与圆有关的计算
17.(遵义中考)如图,半圆的圆心为点O,直径AB的长为12,C为半圆上一点,∠CAB=30°,的长是(D)
A.12π
B.6π
C.5π
D.4π
18.已知扇形的圆心角为60°,半径长为12,则扇形的面积为(D)
A.π
B.2π
C.3π
D.24π
19.如图,已知⊙O的周长等于8π
cm,则圆内接正六边形ABCDEF的边心距OM的长为(B)
A.2
cm
B.2
cm
C.4
cm
D.4
cm
20.如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=2,点D是AB的中点,连接DO并延长交⊙O于点P,过点P作PF⊥AC于点F.
(1)求劣弧PC的长;(结果保留π)
(2)求阴影部分的面积.(结果保留π)
解:(1)∵点D是AB的中点,PD经过圆心,
∴PD⊥AB.
∵∠A=30°,
∴∠POC=∠AOD=60°,
OA=2OD.
∵PF⊥AC,
∴∠OPF=30°.
∴OF=OP.
∵OA=OC,AD=BD,
∴BC=2OD.
∴OA=BC=2.
∴⊙O的半径为2.
∴劣弧PC的长为=π.
(2)∵OF=OP,
∴OF=1.
∴PF==.
∴S阴影=S扇形-S△OPF=-×1×
=π-.
中档题
21.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长等于(C)
A.
B.
C.8
D.6
22.(巴彦淖尔中考)如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为(A)
A.-
B.-π
C.2-
D.-
23.已知⊙O的半径为r,其内接正六边形,正四边形,正三角形的边长分别为a,b,c,则a∶b∶c的值为(C)
A.1∶2∶3
B.3∶2∶1
C.1∶∶
D.∶∶1
24.如图,圆内接△ABC的外角∠ACH的平分线与圆交于D点,DP⊥AC,垂足是点P,DH⊥BH,垂足是点H,下列结论:①CH=CP;②AD=DB;③AP=BH;④DH为圆的切线.其中一定成立的是(D)
A.①②④
B.①③④
C.②③④
D.①②③
25.如图,一块等边三角形的木板,边长为1,现将木板沿水平线翻滚,那么B点从开始至结束所走过的路径长度为.
26.已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴,y轴分别交于点A,B,点A的坐标为(,0),⊙M的切线OC与直线AB交于点C.则∠ACO=30°.
27.如图,在⊙O中,AB为直径,点B为的中点,直径AB交弦CD于点E,CD=2,AE=5.
(1)求⊙O半径r的值;
(2)点F在直径AB上,连接CF,当∠FCD=∠DOB时,求AF的长.
解:(1)∵AB为直径,点B为的中点,CD=2,
∴AB⊥CD,DE=CD=.
在Rt△ODE中,
∵OD=r,OE=5-r,DE=,
∴r2=(5-r)2+()2,解得r=3.
(2)∵由(1)知,OE=AE-AO=5-3=2,
∴tan∠FCE=tan∠DOB==.
在Rt△FCE中,∵tan∠FCE===,
∴EF=.
∴AF=AE-EF=5-=.
28.(葫芦岛中考)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为点F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=,求图中阴影部分的面积.
解:(1)证明:连接AD,OD,∵AB为直径,
∴∠ADB=90°.
∴AD⊥BC.
∵AC=AB,
∴点D为线段BC的中点.
∵点O为AB的中点,
∴OD为△BAC的中位线.∴OD∥AC.
∵DF⊥AC,∴OD⊥DF.∴DF是⊙O的切线.
(2)在Rt△CFD中,CF=1,DF=,
∴tanC==,CD=2.∴∠C=60°.
∵AC=AB,∴△ABC为等边三角形.∴AB=4.
∵OD∥AC,∴∠DOG=∠BAC=60°.
∴DG=OD·tan∠DOG=2.
∴S阴影=S△ODG-S扇形OBD
=DG·OD-πOB2
=2-π.
综合题
29.如图所示,BC是半圆O的直径,AD⊥BC,垂足为点D,弧长等于弧长,BF与AD,AO分别交于点E,G.求证:
(1)∠DAO=∠FBC;
(2)AE=BE.
证明:(1)连接CF.
∵等于,O为圆心,
∴点G是BF的中点,OG⊥BF.
∵BC是半圆O的直径,
∴CF⊥BF.
∴OG∥CF.
∴∠AOB=∠FCB.
∴∠DAO=90°-∠AOB,∠FBC=90°-∠FCB.
∴∠DAO=∠FBC.
(2)连接AC,AB.
∵l=l,
∴∠BCA=∠ACF=∠ABF.
∵BC为圆的直径,
∴∠BAC=90°.
∴∠ABC+∠ACB=90°.
又∵AD⊥BC,∴∠ADB=90°.
∴∠ABC+∠BAD=90°.
∴∠BAD=∠BCA.
∴∠ABF=∠BAD,
即BE=AE.
