数学六年级下人教新课标4.9 用比例解决问题课件 (共29张)
文档属性
| 名称 | 数学六年级下人教新课标4.9 用比例解决问题课件 (共29张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-21 10:37:45 | ||
图片预览





文档简介
课件29张PPT。第 9 课时 用比例解决问题 4 比例总价一定,单价和数量速度一定,路程和时间 总钱数一定,用去的钱数和剩下的钱数反比例正比例不成比例课后作业探索新知课堂小结当堂检测(1)用正比例知识解决问题
(2)用反比例知识解决问题探究点 1用正比例知识解决问题自主学习,小组交流:
1.阅读题目,理解题意。
2.自己独立完成解答。
3.小组内交流解法。张大妈李奶奶方法一:算术法 28÷8×10
=3.5×10
=35(元)
答:李奶奶家上个月的水费是35元。方法二:比例法解:设李奶奶家上个月的水费是x元。8x=28×10x=35答:李奶奶家上个月的水费是35元。提示:用正比例知识解决问题,要先根据不变量确定
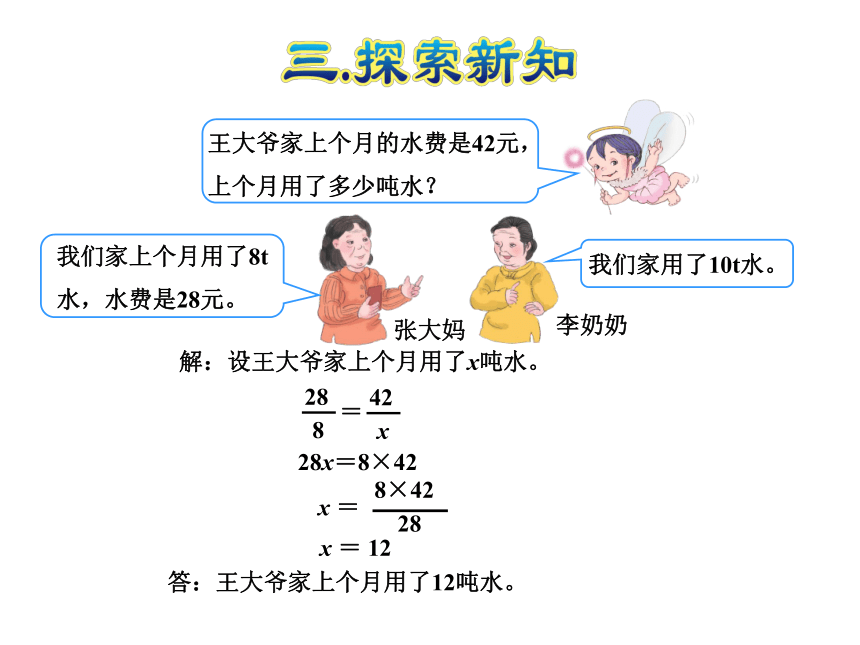
哪两个量成正比例关系,然后列出比例式。 用比例法自主解决,然后小组讨论用比例法解决问
题的步骤。张大妈李奶奶解:设王大爷家上个月用了x吨水。28x=8×42x = 12答:王大爷家上个月用了12吨水。张大妈李奶奶归纳总结:用正比例知识解决问题的步骤:
(1)根据不变量判断题中哪两种相关联的量成正比例。
(2)找出两组相对应的数,并设出未知数,列出比例。
(3)解比例。
(4)检验并写出答语。小试牛刀(选题源于教材P62做一做第1题)1.小明买4支圆珠笔用了6元,小刚想买3支同样的圆珠笔,要用多少钱?解:设要用x元。4x=18x=4.5答:要用4.5元。1.小林读一本文学名著,如果每天读30页,8天可以读完。小林想6天读完,那么平均每天要读多少页?(选题源于教材P64第8题)小试牛刀解:设平均每天要读x页。
6x=30×8
x=40
答:平均每天要读40页。解:设可以买x支。
2x=4×1.5
x =3
答:可以买3支。2.学校小商店有两种圆珠笔。小明带的钱刚好可以买4支单价是1.5元的,如果他只买单价是2元的,可以买多少支?(选题源于教材P62做一做第1题)探究点 2用反比例知识解决问题 一个办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?解:设原来5天的用电量现在可以用x天。25x=100×5x=20答:原来5天的用电量现在可以用20天。现在30天的用电量原来只够用几天?解:设现在30天的用电量原来只够用x天。100x=25×30x=7.5答:现在30天的用电量原来只够用7.5天。 一个办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。
自主独立完成,并想一想用反比例解决问题的步骤是否与用
正比例解决问题类似?提示:用反比例解决问题的步骤与用正比例解决问题的步骤类似。 原来5天的用电量现在可以用多少天?例题5:
解:设李奶奶家上个月的水费是x元。8x=28×10x=35例题6:
解:设原来5天的用电量现在可以用x天。25x=100×5x=20 你能对比两个例题,总结用比例解决问题的一般
步骤吗?先自己试一试,有困难的可以在小组内讨论。归纳总结:用反比例知识解决问题的步骤:
(1)根据不变量判断题中哪两种相关联的量成反比例
关系。
(2)找出两组相对应的数,并设出未知数,列出方程。
(3)解方程。
(4)检验并写出答语。小试牛刀(选题源于教材P62做一做第2题) 学校小商店有两种圆珠笔,小明带的钱刚好可以买4支单价是1.5元的,如果他只买单价是2元的,可以买多少支?解:设如果他只买单价是2元的,可以买x支。2x=4×1.5x=3答:如果他只买单价是2元的,可以买3支。1.小明家用收割机收个小麦。如果每小时收割0.3公顷,40小时能完成任务。(选题源于教材P64第9题)
(1)现在想用30小时收割完,那么每小时应收割多少公顷?小试牛刀解:设每小时应收割x公顷。
30x=40×0.3
x=0.4
答:每小时应收割0.4公顷。(2)每公顷产小麦8 t,这块地共产小麦多少吨?(3)你能提出其他数学问题并解答吗?40×0.3×8=96(t)
答:这块地共产小麦96吨。这块地一共有多少公顷?
40×0.3=12(公顷)
(所提问题不唯一)2.一辆运货汽车从甲地开往乙地,平均每小时行72 km,10小时到达。回来时空车原路返回,每小时可行90 km。多长时间能够返回原地?(选题源于教材P64第10题)解:设x小时能够返回原地。
90x=72×10
x =8
答:8小时能够返回原地。3.小平的姐姐在上大学,妈妈每个月(按30天算)按每天10元的标准给他一笔零花钱。(选题源于教材P64第11题)(1)如果姐姐每天花6元,一个月的零花钱够用多少天?(2)如果姐姐每年花15元,你能提出数学问题并解答吗?解:设一个月的零花钱够用x天。
6x=30×10, x=50
答:一个月的零花钱够用50天。一个月的零花钱够用多少天?
解:设一个月的零花钱够用y天。
15y=30×10, y=20 (所提问题不唯一)4.小东家的客厅是正方形的,用边长为0.6m的方砖铺地,正好需要100块。如果改用边长0.5m的方砖铺地,需要多少块?(选题源于教材P64第12题)解:需要边长为0.5 m的方砖x块。
100×0.62=0.52x x =144
答:需要边长为0.5 m的方砖144块。用比例解决问题:1.用正比例知识解决问题的步骤:
(1)根据不变量判断题中哪两种相关联的量成正比例。
(2)找出两组相对应的数,并设出未知数,列出比例。
(3)解比例。
(4)检验并写出答语。
2.用反比例知识解决问题的步骤:
(1)根据不变量判断题中哪两种相关联的量成反比例关系。
(2)找出两组相对应的数,并设出未知数,列出方程。
(3)解方程。
(4)检验并写出答语。1.填空。
(1)比例尺一定,实际距离和图上距离成( )比例关系。
(2)如果x÷y=6.5×4,那么x和y成( )比例关系。
(3)如果4:x=5:y,那么x和y成( )比例关系。
(4)食堂买3桶油用780元,照这样计算,买8桶油用多少元?
①本题中( )是一定的,( )和( )成( )比例关系。
②如果设买8桶油用x元,那么列出比例式是( )。 正正正每桶油的单价总价桶数正x:8=780:32.用比例解决问题。
(1) 小红的身高是1.6 m,她的影长是2.5 m,如果同一时间、同一地点测得一棵树的影子长4 m,那么这棵树有多高?
(2) 计划在景观大道种800棵观赏树,前8天种了200棵。照这样计算,要完成任务,还需要多少天?
解:设这棵树有x m高。
1.6:2.5=x:4 x= 2.56
答:这棵树有2.56m高。解:设还需要x天。
200:8=(800-200):x
200x= 600×8 x= 24
答:还需要24天。(3) 一种儿童服装买3套需180元钱,照这样计算,420元钱可以买几套?解:设可以买x套。
180:3=420:x
x= 7
答:420元钱可以买7套。
3.填空。
(1)一批零件的个数一定,李师傅每小时生产零件的个数和工作时间成( )比例关系。
(2)从营地到哨卡的路程一定,汽车每小时行驶的路程和行驶的时间成( )比例关系。
(3)某农具厂要生产一批农具,原计划每天生产80件,25天完成,由于改进技术,实际每天生产100件,实际多少天完成任务?
①本题中( )是一定的,( )和( )成( )比例关系。
②如果设实际x天完成任务,那么列出比例式是( )。反反农具的总件数每天生产的件数时间反80×25=100x
4.用比例解决问题。
(1)车队向灾区运送一批救灾物资,去时每小时行60 km,6.5小时到达灾区。回来时每小时行78 km,多长时间能够返回出发地?
(2)一对互相咬合的齿轮,大齿轮有35个齿,每分钟转100转;小齿轮有20个齿,每分钟转多少转?
解:设x小时能够返回出发地。
60×6.5=78x x= 5
答:5小时能够返回出发地。解:设小齿轮每分钟转x转。
35×100=20x x= 175
答:每分钟转175转。5.下面的解法对吗?若不对,请改正。
某工程队修一条公路,4天修了144 m。照这样计算,还要用8天才能完成任务,这条公路一共长多少米?
解:设这条公路一共长x m。
144:4=x:8
x=
x=288
不对。 改正:
解:设这条公路一共长x m。
144:4=x:(4+8)
x= 432
答:5小时能够返回出发地。辨析:不能正确理解正比例和反比例的意义而引起解题错误。
1.阅读题目,理解题意。
2.自己独立完成解答。
3.小组内交流解法。张大妈李奶奶方法一:算术法 28÷8×10
=3.5×10
=35(元)
答:李奶奶家上个月的水费是35元。方法二:比例法解:设李奶奶家上个月的水费是x元。8x=28×10x=35答:李奶奶家上个月的水费是35元。提示:用正比例知识解决问题,要先根据不变量确定
哪两个量成正比例关系,然后列出比例式。 用比例法自主解决,然后小组讨论用比例法解决问
题的步骤。张大妈李奶奶解:设王大爷家上个月用了x吨水。28x=8×42x = 12答:王大爷家上个月用了12吨水。张大妈李奶奶归纳总结:用正比例知识解决问题的步骤:
(1)根据不变量判断题中哪两种相关联的量成正比例。
(2)找出两组相对应的数,并设出未知数,列出比例。
(3)解比例。
(4)检验并写出答语。小试牛刀(选题源于教材P62做一做第1题)1.小明买4支圆珠笔用了6元,小刚想买3支同样的圆珠笔,要用多少钱?解:设要用x元。4x=18x=4.5答:要用4.5元。1.小林读一本文学名著,如果每天读30页,8天可以读完。小林想6天读完,那么平均每天要读多少页?(选题源于教材P64第8题)小试牛刀解:设平均每天要读x页。
6x=30×8
x=40
答:平均每天要读40页。解:设可以买x支。
2x=4×1.5
x =3
答:可以买3支。2.学校小商店有两种圆珠笔。小明带的钱刚好可以买4支单价是1.5元的,如果他只买单价是2元的,可以买多少支?(选题源于教材P62做一做第1题)探究点 2用反比例知识解决问题 一个办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?解:设原来5天的用电量现在可以用x天。25x=100×5x=20答:原来5天的用电量现在可以用20天。现在30天的用电量原来只够用几天?解:设现在30天的用电量原来只够用x天。100x=25×30x=7.5答:现在30天的用电量原来只够用7.5天。 一个办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。
自主独立完成,并想一想用反比例解决问题的步骤是否与用
正比例解决问题类似?提示:用反比例解决问题的步骤与用正比例解决问题的步骤类似。 原来5天的用电量现在可以用多少天?例题5:
解:设李奶奶家上个月的水费是x元。8x=28×10x=35例题6:
解:设原来5天的用电量现在可以用x天。25x=100×5x=20 你能对比两个例题,总结用比例解决问题的一般
步骤吗?先自己试一试,有困难的可以在小组内讨论。归纳总结:用反比例知识解决问题的步骤:
(1)根据不变量判断题中哪两种相关联的量成反比例
关系。
(2)找出两组相对应的数,并设出未知数,列出方程。
(3)解方程。
(4)检验并写出答语。小试牛刀(选题源于教材P62做一做第2题) 学校小商店有两种圆珠笔,小明带的钱刚好可以买4支单价是1.5元的,如果他只买单价是2元的,可以买多少支?解:设如果他只买单价是2元的,可以买x支。2x=4×1.5x=3答:如果他只买单价是2元的,可以买3支。1.小明家用收割机收个小麦。如果每小时收割0.3公顷,40小时能完成任务。(选题源于教材P64第9题)
(1)现在想用30小时收割完,那么每小时应收割多少公顷?小试牛刀解:设每小时应收割x公顷。
30x=40×0.3
x=0.4
答:每小时应收割0.4公顷。(2)每公顷产小麦8 t,这块地共产小麦多少吨?(3)你能提出其他数学问题并解答吗?40×0.3×8=96(t)
答:这块地共产小麦96吨。这块地一共有多少公顷?
40×0.3=12(公顷)
(所提问题不唯一)2.一辆运货汽车从甲地开往乙地,平均每小时行72 km,10小时到达。回来时空车原路返回,每小时可行90 km。多长时间能够返回原地?(选题源于教材P64第10题)解:设x小时能够返回原地。
90x=72×10
x =8
答:8小时能够返回原地。3.小平的姐姐在上大学,妈妈每个月(按30天算)按每天10元的标准给他一笔零花钱。(选题源于教材P64第11题)(1)如果姐姐每天花6元,一个月的零花钱够用多少天?(2)如果姐姐每年花15元,你能提出数学问题并解答吗?解:设一个月的零花钱够用x天。
6x=30×10, x=50
答:一个月的零花钱够用50天。一个月的零花钱够用多少天?
解:设一个月的零花钱够用y天。
15y=30×10, y=20 (所提问题不唯一)4.小东家的客厅是正方形的,用边长为0.6m的方砖铺地,正好需要100块。如果改用边长0.5m的方砖铺地,需要多少块?(选题源于教材P64第12题)解:需要边长为0.5 m的方砖x块。
100×0.62=0.52x x =144
答:需要边长为0.5 m的方砖144块。用比例解决问题:1.用正比例知识解决问题的步骤:
(1)根据不变量判断题中哪两种相关联的量成正比例。
(2)找出两组相对应的数,并设出未知数,列出比例。
(3)解比例。
(4)检验并写出答语。
2.用反比例知识解决问题的步骤:
(1)根据不变量判断题中哪两种相关联的量成反比例关系。
(2)找出两组相对应的数,并设出未知数,列出方程。
(3)解方程。
(4)检验并写出答语。1.填空。
(1)比例尺一定,实际距离和图上距离成( )比例关系。
(2)如果x÷y=6.5×4,那么x和y成( )比例关系。
(3)如果4:x=5:y,那么x和y成( )比例关系。
(4)食堂买3桶油用780元,照这样计算,买8桶油用多少元?
①本题中( )是一定的,( )和( )成( )比例关系。
②如果设买8桶油用x元,那么列出比例式是( )。 正正正每桶油的单价总价桶数正x:8=780:32.用比例解决问题。
(1) 小红的身高是1.6 m,她的影长是2.5 m,如果同一时间、同一地点测得一棵树的影子长4 m,那么这棵树有多高?
(2) 计划在景观大道种800棵观赏树,前8天种了200棵。照这样计算,要完成任务,还需要多少天?
解:设这棵树有x m高。
1.6:2.5=x:4 x= 2.56
答:这棵树有2.56m高。解:设还需要x天。
200:8=(800-200):x
200x= 600×8 x= 24
答:还需要24天。(3) 一种儿童服装买3套需180元钱,照这样计算,420元钱可以买几套?解:设可以买x套。
180:3=420:x
x= 7
答:420元钱可以买7套。
3.填空。
(1)一批零件的个数一定,李师傅每小时生产零件的个数和工作时间成( )比例关系。
(2)从营地到哨卡的路程一定,汽车每小时行驶的路程和行驶的时间成( )比例关系。
(3)某农具厂要生产一批农具,原计划每天生产80件,25天完成,由于改进技术,实际每天生产100件,实际多少天完成任务?
①本题中( )是一定的,( )和( )成( )比例关系。
②如果设实际x天完成任务,那么列出比例式是( )。反反农具的总件数每天生产的件数时间反80×25=100x
4.用比例解决问题。
(1)车队向灾区运送一批救灾物资,去时每小时行60 km,6.5小时到达灾区。回来时每小时行78 km,多长时间能够返回出发地?
(2)一对互相咬合的齿轮,大齿轮有35个齿,每分钟转100转;小齿轮有20个齿,每分钟转多少转?
解:设x小时能够返回出发地。
60×6.5=78x x= 5
答:5小时能够返回出发地。解:设小齿轮每分钟转x转。
35×100=20x x= 175
答:每分钟转175转。5.下面的解法对吗?若不对,请改正。
某工程队修一条公路,4天修了144 m。照这样计算,还要用8天才能完成任务,这条公路一共长多少米?
解:设这条公路一共长x m。
144:4=x:8
x=
x=288
不对。 改正:
解:设这条公路一共长x m。
144:4=x:(4+8)
x= 432
答:5小时能够返回出发地。辨析:不能正确理解正比例和反比例的意义而引起解题错误。
