1.4 整式的乘法(2)同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
1.4整式的乘法（二）同步练习
　班级__________姓名____________总分___________
本节应掌握和应用的知识点
1．单项式与多项式相乘法则：
单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加。
2.能熟练地用法则进行计算。
基础知识和能力拓展精练
1 、选择题
要使（x2+ax+1）（﹣6x3）的展开式中不含x4项，则a应等于（　　）
A．6 B．﹣1 C． ( http: / / www.21cnjy.com / ) D．0
已知ab2=﹣1，则﹣ab（a2b5﹣ab3﹣b）的值等于（　　）
A．﹣1 B．0 C．1 D．无法确定
若7x3y3与一个多项式的积是28x7y3﹣21x5y5+2y （7x3y3）2，则这个多项式为（　　）
A．4x4﹣3x2y2+14x3y4 B．4x2y﹣3x2y2
C．4x4﹣3y2 D．4x4﹣3xy2+7xy3
有16m长的木料（宽度不计），要做成一个如图的窗框．假设窗框横档的长度为x m，那么窗框的面积是( )21cnjy.com
( http: / / www.21cnjy.com / )
A．x（8﹣x）m2 B．x（16﹣x）m2 C．x（8﹣3x）m2 D． ( http: / / www.21cnjy.com / )
下列各题计算正确的是（　　）
A．（ab﹣1）（﹣4ab2）=﹣4a2b3﹣4ab2 B．（3x2+xy﹣y2） 3x2=9x4+3x3y﹣y2
C．（﹣3a）（a2﹣2a+1）=﹣3a3+6a2 D．（﹣2x）（3x2﹣4x﹣2）=﹣6x3+8x2+4x
下列各式中计算错误的是（　　）
A．2x（2x3+3x﹣1）=4x4+6x2﹣2x B．b（b2﹣b+1）=b3﹣b2+b
C．﹣ ( http: / / www.21cnjy.com / )﹣x D． ( http: / / www.21cnjy.com / )x
化简5a （2a2﹣ab），结果正确的是（　　）
A．﹣10a3﹣5ab B．10a3﹣5a2b C．﹣10a2+5a2b D．﹣10a3+5a2b
计算：（2x2）3﹣6x3（x3+2x2+x）=（　　）
A．﹣12x5﹣6x4 B．2x6+12x5+6x4 C．x2﹣6x﹣3 D．2x6﹣12x5﹣6x4
下列运算中正确的是（　　）
A．a3+a4=a12 B．2（a+1）=2a+1
C．（﹣2a3）2=8a5 D．（3a2﹣a3） a=3a3﹣a4
计算所得结果（ ）
A． B． C． 1 D． 2
1 、填空题
如果2x2y A=6x2y2﹣4x3y2，则A=　 　．
计算：x2y（x﹣1﹣y﹣1）=　 　．
若x2（2xm﹣3xn）=2x5﹣3x3，则m=　 　；n=　 　．
若（x2+ax+1） （﹣6x3）的展开式中，不含有x4项，则3a﹣1的值为　 　．
5m2n（2n+3m﹣n2）的计算结果是　 　次多项式．
1 、解答题
（ ( http: / / www.21cnjy.com / )） ( http: / / www.21cnjy.com / )．
计算：
（1）﹣10+6×2﹣1﹣（﹣2）3
（2）（﹣2ab） （2a2+ab﹣2b2）
计算：
（1）（﹣3）0+（﹣ ( http: / / www.21cnjy.com / )）﹣2÷|﹣2|
（2）（﹣4ax）2（5a2﹣3ax2）
（1）（4a﹣b）（﹣2b）2
（2）2mn（﹣2mn）2﹣3n（mn+m2n）﹣mn2．
某同学在计算一个多项式乘以﹣3x2时， ( http: / / www.21cnjy.com )因抄错运算符号，算成了加上﹣3x2 ， 得到的结果是x2﹣4x+1，那么正确的计算结果是多少？ www.21-cn-jy.com
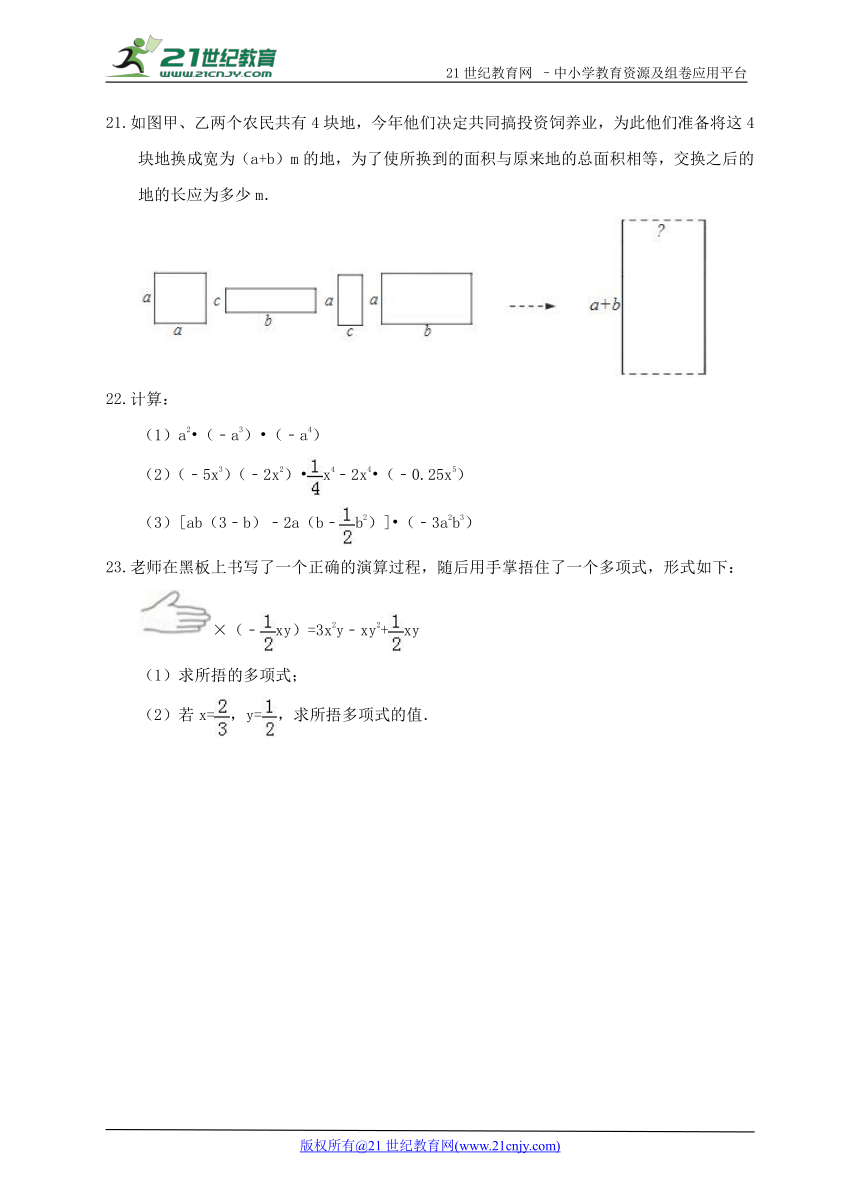
如图甲、乙两个农民共有4块地，今年他们决 ( http: / / www.21cnjy.com )定共同搞投资饲养业，为此他们准备将这4块地换成宽为（a+b）m的地，为了使所换到的面积与原来地的总面积相等，交换之后的地的长应为多少m．2·1·c·n·j·y
( http: / / www.21cnjy.com / )
计算：
（1）a2 （﹣a3） （﹣a4）
（2）（﹣5x3）（﹣2x2） ( http: / / www.21cnjy.com / )x4﹣2x4 （﹣0.25x5）
（3）[ab（3﹣b）﹣2a（b﹣ ( http: / / www.21cnjy.com / )b2）] （﹣3a2b3）
老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如下：
( http: / / www.21cnjy.com / )×（﹣ ( http: / / www.21cnjy.com / )xy）=3x2y﹣xy2+ ( http: / / www.21cnjy.com / )xy
（1）求所捂的多项式；
（2）若x= ( http: / / www.21cnjy.com / )，y= ( http: / / www.21cnjy.com / )，求所捂多项式的值．
答案解析
1 、选择题
【分析】直接利用单项式乘以多项式运算法则结合已知得出a的值．
解：∵（x2+ax+1）（﹣6x3）的展开式中不含x4项，
∴（x2+ax+1）（﹣6x3）=﹣6x5﹣6ax4﹣6x3，中﹣6a=0，
解得：a=0．
故选：D．
【分析】原式利用单项式乘以多项式法则计算，变形后将已知等式代入计算即可求出值．
解：∵ab2=﹣1，
∴原式=﹣（ab2）3+（ab2）2+ab2=1+1﹣1=1，
故选C
【分析】依据因数与积的关系，列出代数式，然后依据多项式除单项式的法则计算即可．
解：∵7x3y3与一个多项式的积是28x7y3﹣21x5y5+2y （7x3y3）2，
∴[28x7y3﹣21x5y5+2y （7x3y3）2]÷7x3y3
=（28x7y3﹣21x5y5+98x6y7）÷7x3y3
=4x4﹣3x2y2+14x3y4．
故选：A．
解：结合图形，显然窗框的另一边是 ( http: / / www.21cnjy.com / )=8﹣ ( http: / / www.21cnjy.com / )x（米）．
根据长方形的面积公式，得：窗框的面积是x（8﹣ ( http: / / www.21cnjy.com / )x）平方米．
故选：D．
【分析】直接利用单项式乘以多项式运算法则分别判断求出即可．
解：A．（ab﹣1）（﹣4ab2）=﹣4a2b3+4ab2，故此选项错误；
B、（3x2+xy﹣y2） 3x2=9x4+3x3y﹣3x2y2，故此选项错误；
C、（﹣3a）（a2﹣2a+1）=﹣3a3+6a2﹣3a，故此选项错误；
D、（﹣2x）（3x2﹣4x﹣2）=﹣6x3+8x2+4x，正确．
故选：D．
【分析】根据单项式与多项式相乘，先用单项式乘多项式的每一项，再把所得的积相加计算即可．
解：A．2x（2x3+3x﹣1）=4x4+6x2﹣2x，故A正确；
B、单项式与多项式相乘，先用单项式乘多项式的每一项，再把所得的积相加计算，故B正确；
C、﹣ ( http: / / www.21cnjy.com / )x（2x2﹣2）=﹣x3+x，故C错误；
D、单项式与多项式相乘，先用单项式乘多项式的每一项，再把所得的积相加计算，故D正确；
故选：C．
【分析】按照单项式乘以多项式的运算法则进行运算即可．
解：5a （2a2﹣ab）=10a3﹣5a2b，
故选：B．
【分析】先算积的乘方，单项式乘多项式，再合并同类项即可求解．
解：（2x2）3﹣6x3（x3+2x2+x）
=8x6﹣6x6﹣12x5﹣6x4
=2x6﹣12x5﹣6x4．
故选：D．
【分析】各项计算得到结果，即可作出判断．
解：A．原式不能合并，错误；
B、原式=2a+2，错误；
C、原式=4a6，错误；
D、原式=3a3﹣a4，正确，
故选D
解：因为=
故选择B
1 、填空题
【分析】直接利用整式的除法运算法则化简求出即可．
解：∵2x2y A=6x2y2﹣4x3y2，
∴A=（6x2y2﹣4x3y2）÷2x2y=3y﹣2xy．
故答案为：3y﹣2xy．
【分析】根据单项式乘以单项式法则求出即可．
解：x2y（x﹣1﹣y﹣1）=xy﹣x2，
故答案为：xy﹣x2．
【分析】首先利用单项式乘以多项式计算出x2（2xm﹣3xn），进而可得2+m=5，2+n=3，再解即可．21教育网
解：x2（2xm﹣3xn）=2x2+m﹣3x2+n，
则2+m=5，2+n=3，
解得：m=3，n=1，
故答案为：3；1．
【分析】原式利用单项式乘以多项式法则计算，合并后根据结果不含x4项求出a的值，即可确定出所求式子的值．21·cn·jy·com
解：原式=﹣6x5﹣6ax4﹣6x3，
∵结果中不含有x4项，∴a=0，
则原式=1﹣1=0．
故答案为：0
【分析】原式利用单项式乘以多项式法则计算即可得到结果．
解：5m2n（2n+3m﹣n2）=10m2n2+15m3n﹣5m2n3，
则计算结果是五次多项式，
故答案为：五
1 、解答题
【分析】根据单项式与多项式相乘，先用单项式乘多项式的每一项，再把所得的积相加计算即可．
解：原式=﹣2x4y﹣ ( http: / / www.21cnjy.com / )x3y2+ ( http: / / www.21cnjy.com / )x2y3．
【分析】（1）先算零指数幂，负整数指数幂，乘方，再计算加减法即可求解；
（2）根据单项式乘多项式的计算法则计算即可求解．
解：（1）﹣10+6×2﹣1﹣（﹣2）3
=﹣1+6× ( http: / / www.21cnjy.com / )﹣（﹣8）
=﹣1+3+8
=10；
（2）（﹣2ab） （2a2+ab﹣2b2）=﹣4a3b﹣2a2b2+4ab3．
【分析】（1）根据0次幂和负整数指数幂，即可解答；
（2）根据单项式乘以多项式，即可解答．
解：（1）原式=1+4÷2
=1+2
=3．
（2）原式=16a2x2（5a2﹣3ax2）
=80a4x2﹣48a3x4
【分析】（1）根据单项式乘多项式的法则进行计算即可；
（2）根据单项式乘多项式的法则、幂的乘方与积的乘方分别进行计算，即可得出答案．
解：（1）（4a﹣b）（﹣2b）2=（4a﹣b） 4b2=16ab2﹣4b3；
（2）2mn（﹣2mn）2﹣3n（mn+m ( http: / / www.21cnjy.com )2n）﹣mn2=2mn 4m2n2﹣3mn2﹣3m2n2﹣mn2=8m3n3﹣3mn2﹣3m2n2﹣mn2=8m3n3﹣4mn2﹣3m2n2．21世纪教育网版权所有
【分析】用错误结果减去已知多项式，得出原式，再乘以﹣3x2得出正确结果．
解：这个多项式是（x2﹣4x+1）﹣（﹣3x2）=4x2﹣4x+1，
正确的计算结果是：（4x2﹣4x+1） （﹣3x2）=﹣12x4+12x3﹣3x2 ．
【分析】先求出原4块地的总面积，再分解因式，即可得出答案．
解：∵原来4块地的总面积为（a2+bc+ac+ab）m2
∴a2+bc+ac+ab=a（a+b）+c（a+b）=（a+b）（a+c），
∵此块地的宽为（a+b）m，
∴交换后这块土地的长为（a+c）m．
【分析】（1）直接利用同底数幂的乘法运算法则化简求出答案；
（2）直接利用单项式乘以单项式运算法则以及结合合并同类项法则化简求出答案；
（3）直接利用单项式乘以单项式运算法则以及合并同类项法则、单项式乘以多项式运算法则化简求出答案．
解：（1）a2 （﹣a3） （﹣a4）=a9；
（2）（﹣5x3）（﹣2x2） ( http: / / www.21cnjy.com / )x4﹣2x4 （﹣0.25x5）
=10x5× ( http: / / www.21cnjy.com / )x4+2x4× ( http: / / www.21cnjy.com / )x5
= ( http: / / www.21cnjy.com / )x9+ ( http: / / www.21cnjy.com / )x9
=3x9；
（3）[ab（3﹣b）﹣2a（b﹣ ( http: / / www.21cnjy.com / )b2）] （﹣3a2b3）
=[（3ab﹣ab2）﹣2ab+ab2] （﹣3a2b3）
=ab （﹣3a2b3）
=﹣3a3b4．
【分析】（1）设多项式为A，则A=（3x2y﹣xy2+ ( http: / / www.21cnjy.com / )xy）÷（﹣ ( http: / / www.21cnjy.com / )xy）计算即可．
（2）把x= ( http: / / www.21cnjy.com / )，y= ( http: / / www.21cnjy.com / )代入多项式求值即可．
解：（1）设多项式为A，
则A=（3x2y﹣xy2+ ( http: / / www.21cnjy.com / )xy）÷（﹣ ( http: / / www.21cnjy.com / )xy）=﹣6x+2y﹣1．
（2）∵x= ( http: / / www.21cnjy.com / )，y= ( http: / / www.21cnjy.com / )，
∴原式=﹣6× ( http: / / www.21cnjy.com / )+2× ( http: / / www.21cnjy.com / )﹣1=﹣4+1﹣1=﹣4．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)