第五章 平面直角坐标系复习学案(无答案)
文档属性
| 名称 | 第五章 平面直角坐标系复习学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 446.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-24 13:51:05 | ||
图片预览



文档简介
平面直角坐标系
诊断性测试
1.若点A在轴上,则点B在…………………( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,点P(-3,5)关于x轴的对称点的坐标为 ( )
A.( ,) B.(3,5) C.(3.) D.(5,)
3. 若点P在第四象限,且到两条坐标轴的距离都是4,则点P的坐标为 ( )
A.(-4,4) B.(-4,-4) C.(4,-4) D.(4,4)
4.在平面直角坐标系中,将点P(﹣2,1)向右平移3个单位长度,再向上平移4个单位长度得到点P′的坐标是 ( )
A.(2,4) B.(1,5) C.(1,-3) D.(-5,5)
5、根据下列表述,能确定位置的是( )
A.光明电影院三排 B.某市大桥南路
C.北偏东30° D.东经118°,北纬45°
6.点 P(3a-2,a﹣3)在第三象限,则a的取值范围是 .
7.点A(﹣5,﹣8)关于y轴的对称点的坐标是 .
8.点P(a+1,a-1)在平面直角坐标系的y轴上,则点P坐标为________.
9、在平面直角坐标系中,一青蛙从点A(-1,0)处向左跳2个单位长度,再向下跳2个单位长度到点A′处,则点A′的坐标为 .
10.在平面直角坐标第中,线段AB的两个端点的坐标分别为,将线段AB经过平移后得到线段,若点A的对应点为,则点B的对应点的坐标是 .
11.如图,若在象棋盘上建立直角坐标系,使“帥”位于点(-1,-2),“馬”位于点(2,-2). 写出“兵”位于的点的坐标 .
12、己知点O(0,0),B(1,2),点A在坐标轴上,且三角形OAB的面积等于2,求满足条件的点A的坐标
例题解析
一、坐标系中,点坐标的特征, 点的对称性, 点到x,y轴的距离
在平面直角坐标系中,A、B点的位置如图所示,
(1)写出A、B两点的坐标: .
(2)若C(﹣3,﹣4)、D(3,﹣3),请在图示坐标系中标出C、D两点.
(3)写出A、B、C、D四点到x轴和y轴的距离:A 到x轴的距离为 ,到y轴的距离为 .B 到x轴的距离为 ,到y轴的距离为 .
C(﹣3,﹣4)到x轴的距离为 ,到y轴的距离为 .D(3,﹣3 )到x轴的距离为 ,到y轴的距离为 .
(4)分析(3)中点的坐标与该点到坐标轴的距离的关系,利用你所发现的结论写出点P(x,y)到x轴的距离为 ,到y轴的距离为 .
坐标轴上点的特征:________________________________
象限内点坐标的特征:_______________________________
关于x,y轴对称的点的坐标特征:_________________________________________
设A(X1,Y1)、B(X2,Y2),则
练习:
1、已知P点坐标为(2a+1,a-3)
①点P在x轴上,则a= ;②点P在y轴上,则a= ;
③点P在第三象限内,则a的取值范围是 ;
④点P在第四象限内,则a的取值范围是 .
2、在直角坐标系中,点A(-3,m)与点B(n,1)关于y轴对称,则m=_______,n=_______.
关于y轴对称,则m=_______,n=_______.
3、点P(a,3)到y轴的距离为4,则a的值为_______.点P(5,-12)到原点的距离是_______.
4、A(2,4), B(1,3),则A、B间的距离是______________
5、若点A(a-2,3)和点B(-1,b+5)关于y轴对称,则点C(a,b)在( )
6. 如图,将正六边形ABCDEF放入平面直角坐标系后,若点A、B、E的坐标分别为(a,b)、(3,1)、(-a,b),则点D的坐标为( )
A.(1,3)
B.(3,-1)
C.(-1,-3)
D.(-3,1)
7. 在平面直角坐标系中,有点A(-2,a+3),B(b,b-3). (1)当点A在第二象限的角平分线上时,求a的值; (2)当点B到x轴的距离是它到y轴的距离2倍时,求点B所在的象限位置.
二、点的平移
1、在直角坐标系中,点A(2,1)向左平移4个单位长度,再向下平移2个单位长度后的坐标为( )
2. 如图,平面直角坐标系中,A、B两点的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,则a,b的值分别为( )
A.1,3
B.1,2
C.2,1
D.1,1
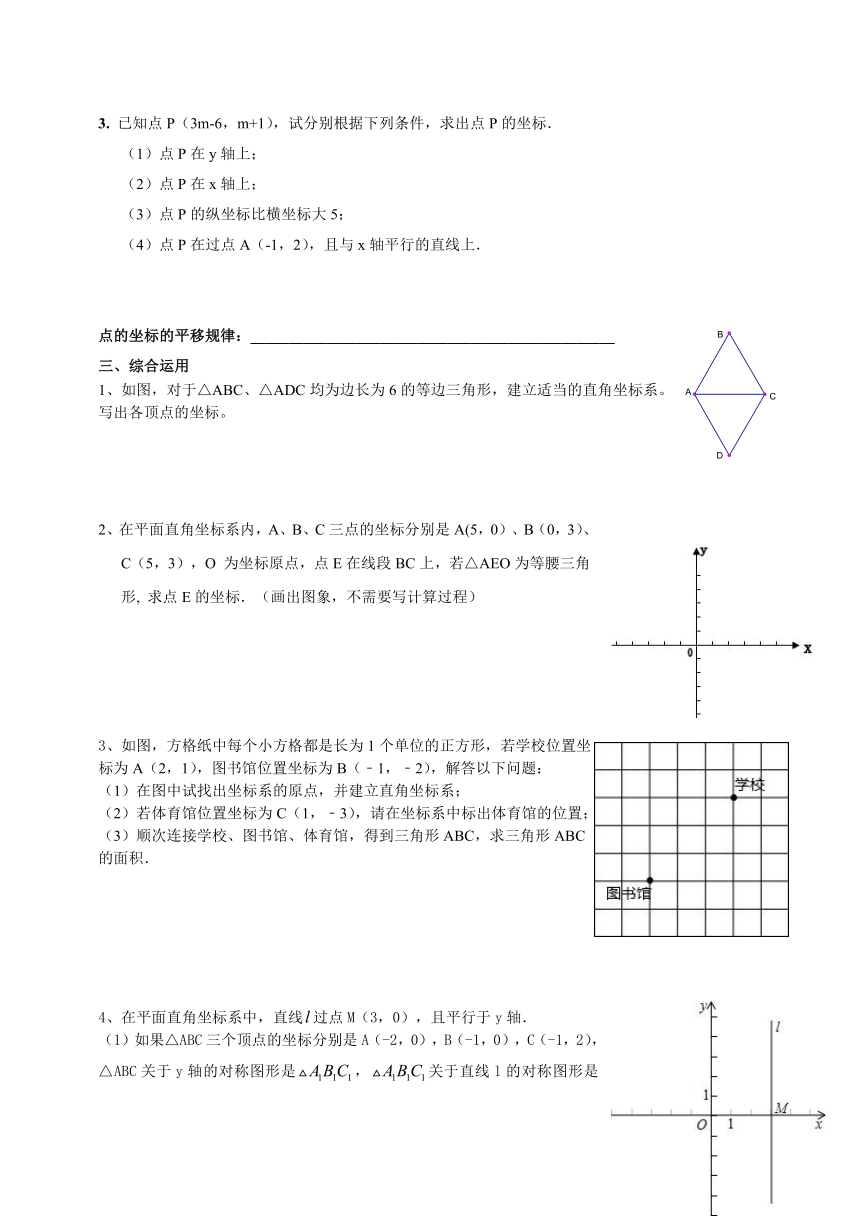
3. 已知点P(3m-6,m+1),试分别根据下列条件,求出点P的坐标. (1)点P在y轴上; (2)点P在x轴上; (3)点P的纵坐标比横坐标大5; (4)点P在过点A(-1,2),且与x轴平行的直线上.
点的坐标的平移规律:________________________________________________
三、综合运用
1、如图,对于△ABC、△ADC均为边长为6的等边三角形,建立适当的直角坐标系。
写出各顶点的坐标。
2、在平面直角坐标系内,A、B、C三点的坐标分别是A(5,0)、B(0,3)、C(5,3),O 为坐标原点,点E在线段BC上,若△AEO为等腰三角形, 求点E的坐标.(画出图象,不需要写计算过程)
3、如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(﹣1,﹣2),解答以下问题:
(1)在图中试找出坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为C(1,﹣3),请在坐标系中标出体育馆的位置;
(3)顺次连接学校、图书馆、体育馆,得到三角形ABC,求三角形ABC的面积.
4、在平面直角坐标系中,直线过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形是,关于直线l的对称图形是,写出的三个顶点的坐标;
(2)如果点P的坐标是,其中,点P关于y轴的对称点是,点关于直线的对称点是,求的长.
拓展训练
1.在平面直角坐标系中,对于平面内任一点(m,n), 规定以下两种变换: (1)f(m,n)=(m,-n),如f(2,1)=(2,-1); (2)g(m,n)=(-m,-n),如g(2,1)=(-2,-1). 按照以上变换有:f[g(3,4)]=f(-3,-4)=(-3,4),那么g[f(2,-3)]=_____________
2.在平面直角坐标系中,已知点A(﹣,0),B(,0),点C在坐标轴上,且AC+BC=6,写出满足条件的所有点C标 .
3.在平面直角坐标系中,点P(m-3,4-2m)不可能在第_______象限
4、已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动).
(1)写出B点的坐标( );
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
4.已知点M(3,2)与点N(x,y)在同一条平行于x轴的直线上,且点N到y轴的距离为5,试求点N的坐标.
5.如图,A(-1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积.
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10,若存在,请直接写出点P的坐标;若不存在,请说明理由.
6. 如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
提高训练
1.已知等腰△ABC,建立适当的直角坐标系后,其三个顶点的坐标分别为A(m,0).B(m+4,2),C(m+4,-3),则下列关于该三角形三边关系正确的是( )
A.AC=BC≠AB
B.AB=AC≠BC
C.AB=BC≠AC
D.AB=AC=BC
2.如图,一个点在第一象限及x轴、y轴上运动,且每秒移动一个单位,在第1秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动[即(0,0)→(0,1)→(1,1)→(1,0)→…],那么第35秒时质点所在位置的坐标是( )
A.(4,0)
B.(0,5)
C.(5,0)
D.(5,5)
3.在平面直角坐标系中,规定把一个三角形先沿x轴翻折,再向右平移两个单位称为一次变换,如图,已知等边三角形ABC的顶点B、C的坐标分别是,(-1,-1),(-3,-1),把三角形ABC经过连续12次这样的变换得到三角形A’B’C’,则点A的对应点A’的坐标是 .
4.在平面直角坐标系xOy中,对于任意三点A、B、C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.
例如:三点坐标分别为A(1,2),B(﹣3,1),C(2,﹣2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.
(1)已知点A(1,2),B(﹣3,1),P(0,t).
①若A、B、P三点的“矩面积”为12,求点P的坐标;
②A、B、P三点的“矩面积”的最小值为 .
(2)已知点E(4,0),F(0,2)M(m,4m),其中m>0.若E、F、M三点的“矩面积”的为8,求m的取值范围.
5.阅读下列一段文字,然后回答下列问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离,
同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2-x1|或|y2-y1|.
(1)已知A(2,4)、B(-3,-8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,试求A、B两点间的距离.
(3)已知一个三角形各顶点坐标为A(0,6)、B(-3,2)、C(3,2),你能判定此三角形的形状吗?说明理由.
6.已知:A(-2,0)、B(2,4),C(5,0) (1)在如图所示的坐标系中描出各点,画出△ABC. (2)求△ABC的面积; (3)点P是y轴负半轴上一动点,连接BP交x轴于点D,是否存在点P使△ADP与△BDC的面积相等?若存在,请直接写出点P的坐标;若不存在,请说明理由.
巩固练习
1、已知P点坐标为(2a+1,a-3)①点P在x轴上,则a= ; ②点P在y轴上,则a= ; ③点P在第三象限内,则a的取值范围是 ; ④点P在第四象限内,则a的取值范围是 。
2、若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为 。
3、一正三角形ABC,A(0,0),B(-4,0),C(-2,),将三角形ABC绕原点顺时针旋转1200得到的三角形的三个顶点坐标分别是 。
4、点P(3,)与点Q(b,2)关于y轴对称,则a= ,b= 。
5、点P(-3,4),它到x轴的距离为 ,到y轴的距离为 ,到原点的距离为 。
6、已知A、B、C三点的坐标分别是(0,0),(5,0),(5,3),且这3点是一个平行四边形的顶点,请同学们写出第四点D的坐标
7.在平面直角坐标系中,O为坐标原点,点A的坐标为(1,),M为坐标轴上一点,且使得△MOA为等腰三角形,则满足条件的点M的个数为 ( )
A. 4 B.5 C.6 D.8
8.如图,直角三角形OAB中,∠AOB=90°,∠A=60°∠xOA=30°,
AB与y轴的交点坐标D为(0,4)。求A、B的坐标。
9、[阅读材料,获取新知] 在航空、航海等领域我们经常用距离和角度来确定点的位置.规定如下:在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,在选定一个单位长度和角度的正方向(通常取逆时针方向).对于平面内任何一点M,用ρ表示线段OM(有时也用r表示),θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对(ρ,θ)就叫点M的极坐标,这样建立的坐标系叫做极坐标系.通常情况下,M的极径坐标单位为1(长度单位),极角坐标单位为rad(或°). 例如:如图①,点M到点O的距离为5个单位长度,OM与Ox的夹角70°(Ox的逆时针方向),则点M的极坐标为(5,70°);同理,点N到点O的距离为3个单位长度,ON与Ox的夹角50°(Ox的顺时针方向),则点N的极坐标为(3,-50°). [利用新知,解答问题] 请根据以上信息,回答下列问题: 如图②,已知过点O的所有射线等分圆周且相邻两射线的夹角为15°. (1)点A的极坐标是______;点D的极坐标是————————————————
(2)请在图②中标出点B(5,45°),点E(2,-90°); (3)怎样从点B运动到点C? 小明设计的一条路线为:点B→(4,45°)→(3,45°)→(3,30°)→点C.请你设计与小明不
同的一条路线,也可以从点B运动到点C.
10、在平面直角坐标系中,横坐标、纵坐标都为整数的点叫做整点.设坐标轴的单位长度为1cm,整点P从原点O出发,速度为1cm/s,且整点P只做向右或向上运动,则运动1s后它可以到达(0,1)、(1,0)两个整点;它运动2s后可以到达(2,0)、(1,1)、(0,2)三个整点;运动3s后它可以到达(3,0)、(2,1)、(1,2)、(0,3)四个整点;…
请探索并回答下面问题:
(1)当整点P从点O出发4s后可以到达的整点共有 个;
(2)在直角坐标系中描出:整点P从点O出发8s后所能到达的整点,并观察这些整点,说出它们在位置上有什么特点?
(3)当整点P从点O出发 s后可到达整点(13,5)的位置.
12.如图,在平面直角坐标系中,线段AB的两个端点的坐标分别为(1,2)、(4,1), (1)线段A1B1是由线段AB经过平移得到的,则点A1的坐标是( , ),
(2)线段A2B2是由线段A1B1经过怎样的变换得到的? (3)若点P(a,b)为线段AB上任意一点,经过上述两次变换后得到点P′,写出点P′的坐标.
诊断性测试
1.若点A在轴上,则点B在…………………( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,点P(-3,5)关于x轴的对称点的坐标为 ( )
A.( ,) B.(3,5) C.(3.) D.(5,)
3. 若点P在第四象限,且到两条坐标轴的距离都是4,则点P的坐标为 ( )
A.(-4,4) B.(-4,-4) C.(4,-4) D.(4,4)
4.在平面直角坐标系中,将点P(﹣2,1)向右平移3个单位长度,再向上平移4个单位长度得到点P′的坐标是 ( )
A.(2,4) B.(1,5) C.(1,-3) D.(-5,5)
5、根据下列表述,能确定位置的是( )
A.光明电影院三排 B.某市大桥南路
C.北偏东30° D.东经118°,北纬45°
6.点 P(3a-2,a﹣3)在第三象限,则a的取值范围是 .
7.点A(﹣5,﹣8)关于y轴的对称点的坐标是 .
8.点P(a+1,a-1)在平面直角坐标系的y轴上,则点P坐标为________.
9、在平面直角坐标系中,一青蛙从点A(-1,0)处向左跳2个单位长度,再向下跳2个单位长度到点A′处,则点A′的坐标为 .
10.在平面直角坐标第中,线段AB的两个端点的坐标分别为,将线段AB经过平移后得到线段,若点A的对应点为,则点B的对应点的坐标是 .
11.如图,若在象棋盘上建立直角坐标系,使“帥”位于点(-1,-2),“馬”位于点(2,-2). 写出“兵”位于的点的坐标 .
12、己知点O(0,0),B(1,2),点A在坐标轴上,且三角形OAB的面积等于2,求满足条件的点A的坐标
例题解析
一、坐标系中,点坐标的特征, 点的对称性, 点到x,y轴的距离
在平面直角坐标系中,A、B点的位置如图所示,
(1)写出A、B两点的坐标: .
(2)若C(﹣3,﹣4)、D(3,﹣3),请在图示坐标系中标出C、D两点.
(3)写出A、B、C、D四点到x轴和y轴的距离:A 到x轴的距离为 ,到y轴的距离为 .B 到x轴的距离为 ,到y轴的距离为 .
C(﹣3,﹣4)到x轴的距离为 ,到y轴的距离为 .D(3,﹣3 )到x轴的距离为 ,到y轴的距离为 .
(4)分析(3)中点的坐标与该点到坐标轴的距离的关系,利用你所发现的结论写出点P(x,y)到x轴的距离为 ,到y轴的距离为 .
坐标轴上点的特征:________________________________
象限内点坐标的特征:_______________________________
关于x,y轴对称的点的坐标特征:_________________________________________
设A(X1,Y1)、B(X2,Y2),则
练习:
1、已知P点坐标为(2a+1,a-3)
①点P在x轴上,则a= ;②点P在y轴上,则a= ;
③点P在第三象限内,则a的取值范围是 ;
④点P在第四象限内,则a的取值范围是 .
2、在直角坐标系中,点A(-3,m)与点B(n,1)关于y轴对称,则m=_______,n=_______.
关于y轴对称,则m=_______,n=_______.
3、点P(a,3)到y轴的距离为4,则a的值为_______.点P(5,-12)到原点的距离是_______.
4、A(2,4), B(1,3),则A、B间的距离是______________
5、若点A(a-2,3)和点B(-1,b+5)关于y轴对称,则点C(a,b)在( )
6. 如图,将正六边形ABCDEF放入平面直角坐标系后,若点A、B、E的坐标分别为(a,b)、(3,1)、(-a,b),则点D的坐标为( )
A.(1,3)
B.(3,-1)
C.(-1,-3)
D.(-3,1)
7. 在平面直角坐标系中,有点A(-2,a+3),B(b,b-3). (1)当点A在第二象限的角平分线上时,求a的值; (2)当点B到x轴的距离是它到y轴的距离2倍时,求点B所在的象限位置.
二、点的平移
1、在直角坐标系中,点A(2,1)向左平移4个单位长度,再向下平移2个单位长度后的坐标为( )
2. 如图,平面直角坐标系中,A、B两点的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,则a,b的值分别为( )
A.1,3
B.1,2
C.2,1
D.1,1
3. 已知点P(3m-6,m+1),试分别根据下列条件,求出点P的坐标. (1)点P在y轴上; (2)点P在x轴上; (3)点P的纵坐标比横坐标大5; (4)点P在过点A(-1,2),且与x轴平行的直线上.
点的坐标的平移规律:________________________________________________
三、综合运用
1、如图,对于△ABC、△ADC均为边长为6的等边三角形,建立适当的直角坐标系。
写出各顶点的坐标。
2、在平面直角坐标系内,A、B、C三点的坐标分别是A(5,0)、B(0,3)、C(5,3),O 为坐标原点,点E在线段BC上,若△AEO为等腰三角形, 求点E的坐标.(画出图象,不需要写计算过程)
3、如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(﹣1,﹣2),解答以下问题:
(1)在图中试找出坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为C(1,﹣3),请在坐标系中标出体育馆的位置;
(3)顺次连接学校、图书馆、体育馆,得到三角形ABC,求三角形ABC的面积.
4、在平面直角坐标系中,直线过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形是,关于直线l的对称图形是,写出的三个顶点的坐标;
(2)如果点P的坐标是,其中,点P关于y轴的对称点是,点关于直线的对称点是,求的长.
拓展训练
1.在平面直角坐标系中,对于平面内任一点(m,n), 规定以下两种变换: (1)f(m,n)=(m,-n),如f(2,1)=(2,-1); (2)g(m,n)=(-m,-n),如g(2,1)=(-2,-1). 按照以上变换有:f[g(3,4)]=f(-3,-4)=(-3,4),那么g[f(2,-3)]=_____________
2.在平面直角坐标系中,已知点A(﹣,0),B(,0),点C在坐标轴上,且AC+BC=6,写出满足条件的所有点C标 .
3.在平面直角坐标系中,点P(m-3,4-2m)不可能在第_______象限
4、已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动).
(1)写出B点的坐标( );
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
4.已知点M(3,2)与点N(x,y)在同一条平行于x轴的直线上,且点N到y轴的距离为5,试求点N的坐标.
5.如图,A(-1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积.
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10,若存在,请直接写出点P的坐标;若不存在,请说明理由.
6. 如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
提高训练
1.已知等腰△ABC,建立适当的直角坐标系后,其三个顶点的坐标分别为A(m,0).B(m+4,2),C(m+4,-3),则下列关于该三角形三边关系正确的是( )
A.AC=BC≠AB
B.AB=AC≠BC
C.AB=BC≠AC
D.AB=AC=BC
2.如图,一个点在第一象限及x轴、y轴上运动,且每秒移动一个单位,在第1秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动[即(0,0)→(0,1)→(1,1)→(1,0)→…],那么第35秒时质点所在位置的坐标是( )
A.(4,0)
B.(0,5)
C.(5,0)
D.(5,5)
3.在平面直角坐标系中,规定把一个三角形先沿x轴翻折,再向右平移两个单位称为一次变换,如图,已知等边三角形ABC的顶点B、C的坐标分别是,(-1,-1),(-3,-1),把三角形ABC经过连续12次这样的变换得到三角形A’B’C’,则点A的对应点A’的坐标是 .
4.在平面直角坐标系xOy中,对于任意三点A、B、C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.
例如:三点坐标分别为A(1,2),B(﹣3,1),C(2,﹣2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.
(1)已知点A(1,2),B(﹣3,1),P(0,t).
①若A、B、P三点的“矩面积”为12,求点P的坐标;
②A、B、P三点的“矩面积”的最小值为 .
(2)已知点E(4,0),F(0,2)M(m,4m),其中m>0.若E、F、M三点的“矩面积”的为8,求m的取值范围.
5.阅读下列一段文字,然后回答下列问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离,
同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2-x1|或|y2-y1|.
(1)已知A(2,4)、B(-3,-8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,试求A、B两点间的距离.
(3)已知一个三角形各顶点坐标为A(0,6)、B(-3,2)、C(3,2),你能判定此三角形的形状吗?说明理由.
6.已知:A(-2,0)、B(2,4),C(5,0) (1)在如图所示的坐标系中描出各点,画出△ABC. (2)求△ABC的面积; (3)点P是y轴负半轴上一动点,连接BP交x轴于点D,是否存在点P使△ADP与△BDC的面积相等?若存在,请直接写出点P的坐标;若不存在,请说明理由.
巩固练习
1、已知P点坐标为(2a+1,a-3)①点P在x轴上,则a= ; ②点P在y轴上,则a= ; ③点P在第三象限内,则a的取值范围是 ; ④点P在第四象限内,则a的取值范围是 。
2、若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为 。
3、一正三角形ABC,A(0,0),B(-4,0),C(-2,),将三角形ABC绕原点顺时针旋转1200得到的三角形的三个顶点坐标分别是 。
4、点P(3,)与点Q(b,2)关于y轴对称,则a= ,b= 。
5、点P(-3,4),它到x轴的距离为 ,到y轴的距离为 ,到原点的距离为 。
6、已知A、B、C三点的坐标分别是(0,0),(5,0),(5,3),且这3点是一个平行四边形的顶点,请同学们写出第四点D的坐标
7.在平面直角坐标系中,O为坐标原点,点A的坐标为(1,),M为坐标轴上一点,且使得△MOA为等腰三角形,则满足条件的点M的个数为 ( )
A. 4 B.5 C.6 D.8
8.如图,直角三角形OAB中,∠AOB=90°,∠A=60°∠xOA=30°,
AB与y轴的交点坐标D为(0,4)。求A、B的坐标。
9、[阅读材料,获取新知] 在航空、航海等领域我们经常用距离和角度来确定点的位置.规定如下:在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,在选定一个单位长度和角度的正方向(通常取逆时针方向).对于平面内任何一点M,用ρ表示线段OM(有时也用r表示),θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对(ρ,θ)就叫点M的极坐标,这样建立的坐标系叫做极坐标系.通常情况下,M的极径坐标单位为1(长度单位),极角坐标单位为rad(或°). 例如:如图①,点M到点O的距离为5个单位长度,OM与Ox的夹角70°(Ox的逆时针方向),则点M的极坐标为(5,70°);同理,点N到点O的距离为3个单位长度,ON与Ox的夹角50°(Ox的顺时针方向),则点N的极坐标为(3,-50°). [利用新知,解答问题] 请根据以上信息,回答下列问题: 如图②,已知过点O的所有射线等分圆周且相邻两射线的夹角为15°. (1)点A的极坐标是______;点D的极坐标是————————————————
(2)请在图②中标出点B(5,45°),点E(2,-90°); (3)怎样从点B运动到点C? 小明设计的一条路线为:点B→(4,45°)→(3,45°)→(3,30°)→点C.请你设计与小明不
同的一条路线,也可以从点B运动到点C.
10、在平面直角坐标系中,横坐标、纵坐标都为整数的点叫做整点.设坐标轴的单位长度为1cm,整点P从原点O出发,速度为1cm/s,且整点P只做向右或向上运动,则运动1s后它可以到达(0,1)、(1,0)两个整点;它运动2s后可以到达(2,0)、(1,1)、(0,2)三个整点;运动3s后它可以到达(3,0)、(2,1)、(1,2)、(0,3)四个整点;…
请探索并回答下面问题:
(1)当整点P从点O出发4s后可以到达的整点共有 个;
(2)在直角坐标系中描出:整点P从点O出发8s后所能到达的整点,并观察这些整点,说出它们在位置上有什么特点?
(3)当整点P从点O出发 s后可到达整点(13,5)的位置.
12.如图,在平面直角坐标系中,线段AB的两个端点的坐标分别为(1,2)、(4,1), (1)线段A1B1是由线段AB经过平移得到的,则点A1的坐标是( , ),
(2)线段A2B2是由线段A1B1经过怎样的变换得到的? (3)若点P(a,b)为线段AB上任意一点,经过上述两次变换后得到点P′,写出点P′的坐标.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
