5.5 用二次函数解决问题学案(无答案)
文档属性
| 名称 | 5.5 用二次函数解决问题学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 264.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-24 00:00:00 | ||
图片预览




文档简介
二次函数运用
诊断测试
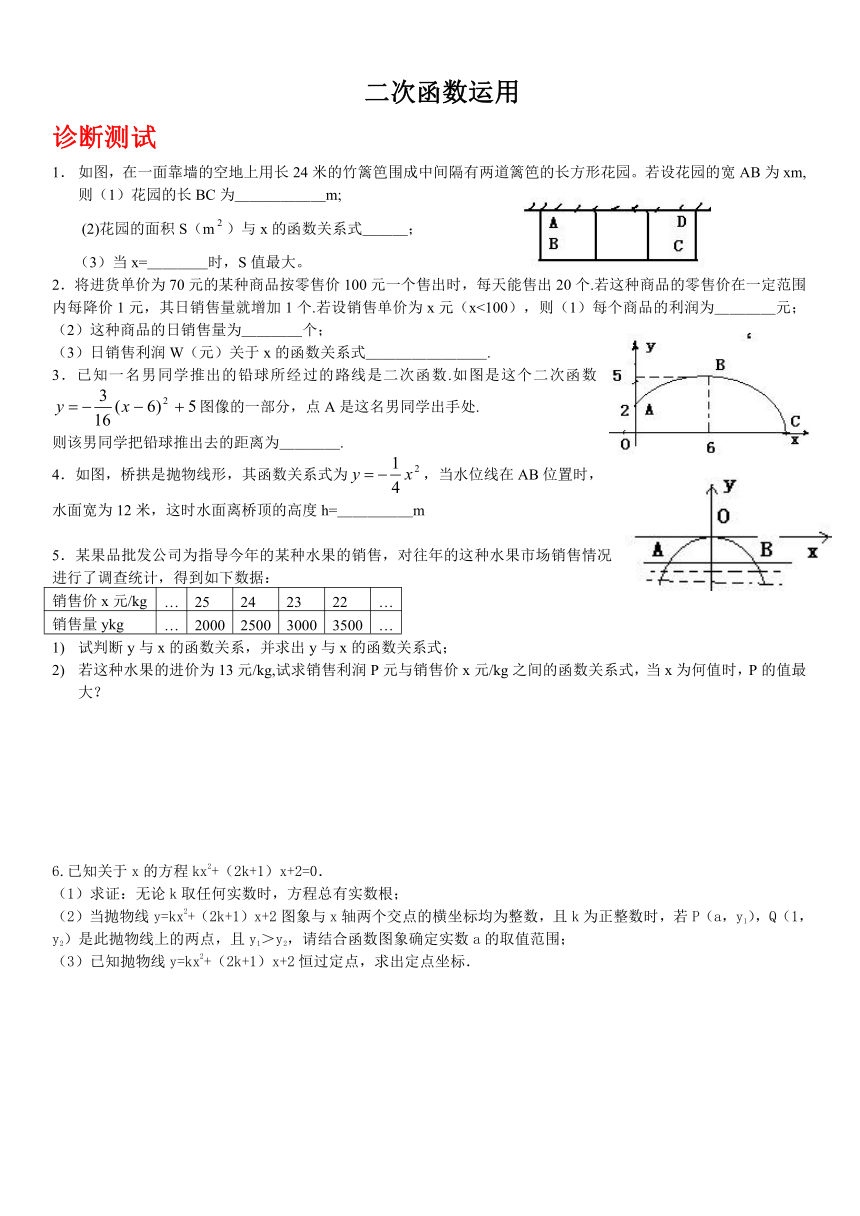
如图,在一面靠墙的空地上用长24米的竹篱笆围成中间隔有两道篱笆的长方形花园。若设花园的宽AB为xm,则(1)花园的长BC为______m;
(2)花园的面积S(m)与x的函数关系式___;
(3)当x=____时,S值最大。
2.将进货单价为70元的某种商品按零售价100元一个售出时,每天能售出20个.若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1个.若设销售单价为x元(x<100),则(1)每个商品的利润为____元;(2)这种商品的日销售量为____个;
(3)日销售利润W(元)关于x的函数关系式________.
3.已知一名男同学推出的铅球所经过的路线是二次函数.如图是这个二次函数图像的一部分,点A是这名男同学出手处.
则该男同学把铅球推出去的距离为____.
4.如图,桥拱是抛物线形,其函数关系式为,当水位线在AB位置时,水面宽为12米,这时水面离桥顶的高度h=_____m
5.某果品批发公司为指导今年的某种水果的销售,对往年的这种水果市场销售情况进行了调查统计,得到如下数据:
销售价x元/kg
…
25
24
23
22
…
销售量ykg
…
2000
2500
3000
3500
…
试判断y与x的函数关系,并求出y与x的函数关系式;
若这种水果的进价为13元/kg,试求销售利润P元与销售价x元/kg之间的函数关系式,当x为何值时,P的值最大?
6.已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2,请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.
基础演练
例1、某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
例2、某瓜果基地市场部为指导该基地某种蔬菜的生产和销售,在对历年市场行情和生产情况进行了调查的基础上,对今年这种蔬菜上市后的市场售价和生产成本进行了预测,提供了两个方面的信息,如图所示.
请你根据图象提供的信息解答:
(1)在3月份出售这种蔬菜,每千克的收益是多少元 (收益=售价-成本)
(2)哪个月出售这种蔬菜,每千克的收益最大 说明理由
1.某网店打出促销广告:最潮新款服装30件,每件售价300元。若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元。已知该服装成本是每件200元。设顾客一次性购买服装件时,该网店从中获利元。
(1)求与的函数关系式,并写出自变量的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
2.某家禽养殖场,用总长为110m的围栏靠墙(墙长为22m)围成如图所示的三块矩形区域,矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半,设AD长为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,y有最大值?最大值是多少?
3.某批发商以40元/千克的价格购入了某种水果500千克.据市场预测,该种水果的售价y(元/千克)与保存时间x(天)的函数关系为y=60+2x,但保存这批水果平均每天将损耗10千克,且最多能保存8天.另外,批发商保存该批水果每天还需40元的费用.
(1)若批发商保存1天后将该批水果一次性卖出,则卖出时水果的售价为_________
(元/千克),获得的总利润为_______________(元);
(2)设批发商将这批水果保存x天后一次性卖出,试求批发商所获得的总利润w(元)与保存时间x(天)之间的函数关系式;
(3)求批发商经营这批水果所能获得的最大利润.
4、某企业生产并销售某种产品,假设销售量与产量相等.下图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
(1)请解释图中点D的横坐标、纵坐标的实际意义.
(2)求线段AB所表示的y1与x之间的函数表达式.
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
例3在体育测试时,初三的一名高个子男生推铅球,已知铅球所经过的路线是某个二次函数的图象的一部分(如图),如果这个男生的出手处A点坐标为(0,2),铅球路线的最高处B的坐标为(6,5)。
(1)求这个二次函数的解析式。
(2)该男生把铅球推出去多远?(精确到0.01米)
1、如图所示,桃河公园要建造圆形喷水池.在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.
(1)如果不计其它因素,那么水池的半径至少要多少m,才能使喷出的水流不致落到池外?
(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5m,要使水流不落到池外,此时水流的最大高度应达到多少m(精确到0.1m)?
2.如图,以40m/s的速度将小球沿与地面成某一角度的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间(单位:s)之间具有函数关系h=20t-5t2.请解答以下问题:
(1)小球的飞行高度能否达到15m?如果能,需要多少飞行时间?
(2)小球的飞行高度能否达到20.5m?为什么?
(3)小球从飞出到落地要用多少时间?
例4、如图,一位篮球运动员在点A处跳起投篮,球沿一条抛物线运行,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮框.
(1)建立如图所示的直角坐标系,求抛物线所对应的函数解析式
(2)若该运动员身高1.8米,这次跳投时,球在他头顶上方0.25米处出手,他跳离地面多高
1、练习:
1、如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣
1/6x2+bx+c表示,且抛物线时的点C到墙面OB的水平距离为3m,到地面OA的距离为
17/2m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
2、
有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
(1)在如图所示的直角坐标系中,求出该抛物线的解析式.
(2)在正常水位的基础上,当水位上升h(m)时,桥下水面的宽度为d(m),试求出用d表示h的函数关系式;
(3)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面的宽度不得小于18m,求水深超过多少米时就会影响过往船只在桥下顺利航行?
3.如图所示是一桥供为抛物线型,在正常水位下测得主拱宽AB=24m,最高点C离水面8m.
建立适当的直角坐标系,求出此主桥拱所在抛物线的函数关系式;
桥边有一浮在水面部分高4m,最宽处12m的小船,试探究此船能否开到桥下?
例6、如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
(1)求二次函数的解析式;
(2)设点A的坐标为(x,y),试求矩形ABCD的周长p关于自变量x的函数解析式,
(3)是否存在这样的矩形ABCD,使它的周长为9?试证明你的结论。
1、在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.
求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
提升拓展
1、“双十一”淘宝网销售一款工艺品,每件的成本是50元.销售期间发现,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当降价了x元时,每天的销售利润是
元(直接写出结果);
(2)当定价多少元时,每天的销售利润最大?最大利润是多少?
(3)如果每天的销售利润不低于4000元,那么每天的总成本至少需要多少元?(每天的总成本=每件的成本×每天的销售量)
2.已知一次函数y=x+4的图象与二次函数y=ax(x﹣2)的图象相交于A(﹣1,b)和B,点P是线段AB上的动点(不与A、B重合),过点P作PC⊥x轴,与二次函数y=ax(x﹣2)的图象交于点C.
(1)求a、b的值
(2)求线段PC长的最大值;
(3)若△PAC为直角三角形,请直接写出点P的坐标.
4.如图,是将抛物线y=-x2平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C.
(1)求抛物线的函数表达式;
(2)若点N为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标;若不存在,说明理由.
课外延伸
1.用
6m
长的铝合金型材做一个形状如图所示的矩形窗框,应做成长、宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?
2.有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为
4m,跨度为
10m,如图所示,把它的图形放在直角坐标系中.
①求这条抛物线所对应的函数关系式.
②如图,在对称轴右边
1m
处,桥洞离水面的高是多少?
3.在美化校园的活动中,某兴趣小组想借助如图16-2所示的直角墙角(两边足够长),用28
m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x
m.
(1)若花园的面积为192
m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15
m和6
m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
5、.如图,抛物线y=ax2-x-2(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,已知B点坐标为(4,0).(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.
知识点一:
题型一、抛物线y=-2x -6x+3,当x=_____时,y有最大值是__________
解决生活中的最优化问题
方法:
1、确定变量,设出变量
2、列函数关系式
3、配方或公式法求最值
4、结论
知识点二:
抛物线y=-2x -6x+3,当x=0时,y=__________,当y=0时,x=_____
解决生活中的x、y轴交点问题(抛球)
方法:
1、设恰当的关系式
2、求函数关系式
3、已知x=0求y值或已知0值求x值
4、结论
知识点三:
抛物线y=-2x -6x+3,当x=-1时,y=______,当y=2时,x=_____
解决生活中的求自变量x或函数值y问题(线段长、通行)
方法:
1、建立适当的平面直角坐标系,数学化点的坐标
2、设恰当的关系式
3、求函数关系式
4、已知x值求y值或已知y值求x值
5.结论
知识点四:
二次函数与图形
综合运用几何图形的判定与性质
诊断测试
如图,在一面靠墙的空地上用长24米的竹篱笆围成中间隔有两道篱笆的长方形花园。若设花园的宽AB为xm,则(1)花园的长BC为______m;
(2)花园的面积S(m)与x的函数关系式___;
(3)当x=____时,S值最大。
2.将进货单价为70元的某种商品按零售价100元一个售出时,每天能售出20个.若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1个.若设销售单价为x元(x<100),则(1)每个商品的利润为____元;(2)这种商品的日销售量为____个;
(3)日销售利润W(元)关于x的函数关系式________.
3.已知一名男同学推出的铅球所经过的路线是二次函数.如图是这个二次函数图像的一部分,点A是这名男同学出手处.
则该男同学把铅球推出去的距离为____.
4.如图,桥拱是抛物线形,其函数关系式为,当水位线在AB位置时,水面宽为12米,这时水面离桥顶的高度h=_____m
5.某果品批发公司为指导今年的某种水果的销售,对往年的这种水果市场销售情况进行了调查统计,得到如下数据:
销售价x元/kg
…
25
24
23
22
…
销售量ykg
…
2000
2500
3000
3500
…
试判断y与x的函数关系,并求出y与x的函数关系式;
若这种水果的进价为13元/kg,试求销售利润P元与销售价x元/kg之间的函数关系式,当x为何值时,P的值最大?
6.已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2,请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.
基础演练
例1、某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
例2、某瓜果基地市场部为指导该基地某种蔬菜的生产和销售,在对历年市场行情和生产情况进行了调查的基础上,对今年这种蔬菜上市后的市场售价和生产成本进行了预测,提供了两个方面的信息,如图所示.
请你根据图象提供的信息解答:
(1)在3月份出售这种蔬菜,每千克的收益是多少元 (收益=售价-成本)
(2)哪个月出售这种蔬菜,每千克的收益最大 说明理由
1.某网店打出促销广告:最潮新款服装30件,每件售价300元。若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元。已知该服装成本是每件200元。设顾客一次性购买服装件时,该网店从中获利元。
(1)求与的函数关系式,并写出自变量的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
2.某家禽养殖场,用总长为110m的围栏靠墙(墙长为22m)围成如图所示的三块矩形区域,矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半,设AD长为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,y有最大值?最大值是多少?
3.某批发商以40元/千克的价格购入了某种水果500千克.据市场预测,该种水果的售价y(元/千克)与保存时间x(天)的函数关系为y=60+2x,但保存这批水果平均每天将损耗10千克,且最多能保存8天.另外,批发商保存该批水果每天还需40元的费用.
(1)若批发商保存1天后将该批水果一次性卖出,则卖出时水果的售价为_________
(元/千克),获得的总利润为_______________(元);
(2)设批发商将这批水果保存x天后一次性卖出,试求批发商所获得的总利润w(元)与保存时间x(天)之间的函数关系式;
(3)求批发商经营这批水果所能获得的最大利润.
4、某企业生产并销售某种产品,假设销售量与产量相等.下图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
(1)请解释图中点D的横坐标、纵坐标的实际意义.
(2)求线段AB所表示的y1与x之间的函数表达式.
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
例3在体育测试时,初三的一名高个子男生推铅球,已知铅球所经过的路线是某个二次函数的图象的一部分(如图),如果这个男生的出手处A点坐标为(0,2),铅球路线的最高处B的坐标为(6,5)。
(1)求这个二次函数的解析式。
(2)该男生把铅球推出去多远?(精确到0.01米)
1、如图所示,桃河公园要建造圆形喷水池.在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.
(1)如果不计其它因素,那么水池的半径至少要多少m,才能使喷出的水流不致落到池外?
(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5m,要使水流不落到池外,此时水流的最大高度应达到多少m(精确到0.1m)?
2.如图,以40m/s的速度将小球沿与地面成某一角度的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间(单位:s)之间具有函数关系h=20t-5t2.请解答以下问题:
(1)小球的飞行高度能否达到15m?如果能,需要多少飞行时间?
(2)小球的飞行高度能否达到20.5m?为什么?
(3)小球从飞出到落地要用多少时间?
例4、如图,一位篮球运动员在点A处跳起投篮,球沿一条抛物线运行,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮框.
(1)建立如图所示的直角坐标系,求抛物线所对应的函数解析式
(2)若该运动员身高1.8米,这次跳投时,球在他头顶上方0.25米处出手,他跳离地面多高
1、练习:
1、如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣
1/6x2+bx+c表示,且抛物线时的点C到墙面OB的水平距离为3m,到地面OA的距离为
17/2m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
2、
有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
(1)在如图所示的直角坐标系中,求出该抛物线的解析式.
(2)在正常水位的基础上,当水位上升h(m)时,桥下水面的宽度为d(m),试求出用d表示h的函数关系式;
(3)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面的宽度不得小于18m,求水深超过多少米时就会影响过往船只在桥下顺利航行?
3.如图所示是一桥供为抛物线型,在正常水位下测得主拱宽AB=24m,最高点C离水面8m.
建立适当的直角坐标系,求出此主桥拱所在抛物线的函数关系式;
桥边有一浮在水面部分高4m,最宽处12m的小船,试探究此船能否开到桥下?
例6、如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
(1)求二次函数的解析式;
(2)设点A的坐标为(x,y),试求矩形ABCD的周长p关于自变量x的函数解析式,
(3)是否存在这样的矩形ABCD,使它的周长为9?试证明你的结论。
1、在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.
求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
提升拓展
1、“双十一”淘宝网销售一款工艺品,每件的成本是50元.销售期间发现,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当降价了x元时,每天的销售利润是
元(直接写出结果);
(2)当定价多少元时,每天的销售利润最大?最大利润是多少?
(3)如果每天的销售利润不低于4000元,那么每天的总成本至少需要多少元?(每天的总成本=每件的成本×每天的销售量)
2.已知一次函数y=x+4的图象与二次函数y=ax(x﹣2)的图象相交于A(﹣1,b)和B,点P是线段AB上的动点(不与A、B重合),过点P作PC⊥x轴,与二次函数y=ax(x﹣2)的图象交于点C.
(1)求a、b的值
(2)求线段PC长的最大值;
(3)若△PAC为直角三角形,请直接写出点P的坐标.
4.如图,是将抛物线y=-x2平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C.
(1)求抛物线的函数表达式;
(2)若点N为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标;若不存在,说明理由.
课外延伸
1.用
6m
长的铝合金型材做一个形状如图所示的矩形窗框,应做成长、宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?
2.有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为
4m,跨度为
10m,如图所示,把它的图形放在直角坐标系中.
①求这条抛物线所对应的函数关系式.
②如图,在对称轴右边
1m
处,桥洞离水面的高是多少?
3.在美化校园的活动中,某兴趣小组想借助如图16-2所示的直角墙角(两边足够长),用28
m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x
m.
(1)若花园的面积为192
m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15
m和6
m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
5、.如图,抛物线y=ax2-x-2(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,已知B点坐标为(4,0).(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.
知识点一:
题型一、抛物线y=-2x -6x+3,当x=_____时,y有最大值是__________
解决生活中的最优化问题
方法:
1、确定变量,设出变量
2、列函数关系式
3、配方或公式法求最值
4、结论
知识点二:
抛物线y=-2x -6x+3,当x=0时,y=__________,当y=0时,x=_____
解决生活中的x、y轴交点问题(抛球)
方法:
1、设恰当的关系式
2、求函数关系式
3、已知x=0求y值或已知0值求x值
4、结论
知识点三:
抛物线y=-2x -6x+3,当x=-1时,y=______,当y=2时,x=_____
解决生活中的求自变量x或函数值y问题(线段长、通行)
方法:
1、建立适当的平面直角坐标系,数学化点的坐标
2、设恰当的关系式
3、求函数关系式
4、已知x值求y值或已知y值求x值
5.结论
知识点四:
二次函数与图形
综合运用几何图形的判定与性质
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
