山东省聊城市高唐县2017-2018学年八年级数学上学期期中试题青岛版(含答案)
文档属性
| 名称 | 山东省聊城市高唐县2017-2018学年八年级数学上学期期中试题青岛版(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 232.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-23 00:00:00 | ||
图片预览



文档简介
2017-2018学年第一学期期中考试八年级数学试题
(时间:120分钟,满分:120分)
一、选择题(本大题共12小题,共36分)
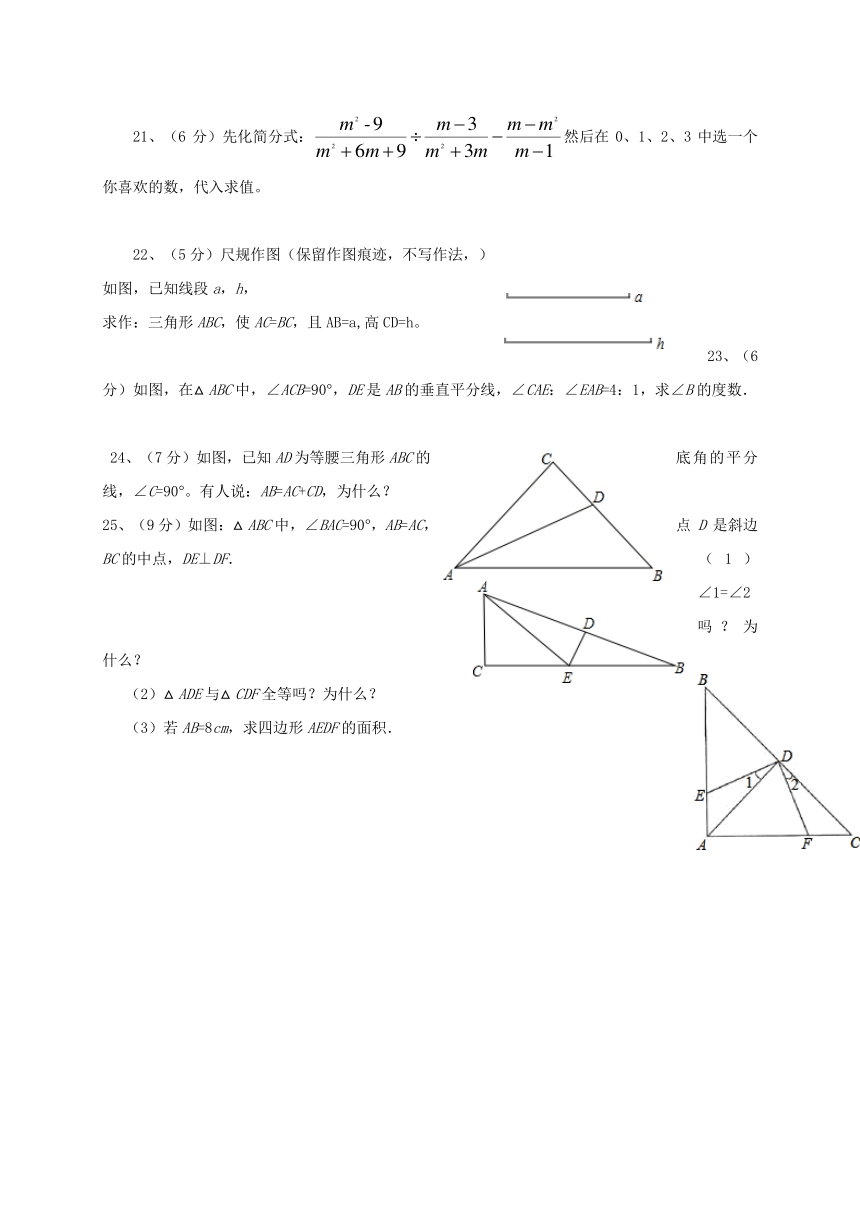
如图,两个三角形为全等三角形,则∠α的度数是( )
A. 72°
B. 60°
C. 58°
D. 50°
如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
A. AC=BC+CE
B. ∠A=∠2
C. △ABC≌△CED
D. ∠A与∠D互余
下面四个图形分别是低碳、节水、节能和绿色食品标志,在这四个标志中,是轴对称图形的是( )
A.
B.
C.
D.
如图,如果直线m是多边形ABCDE的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )
A. 60°
B. 50°
C. 40°
D. 70°
到三角形的三个顶点距离相等的点是( )
A. 三条角平分线的交点
B. 三条中线的交点
C. 三条高的交点
D. 三条边的垂直平分线的交点
如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D.若CD=3cm,则点D到AB的距离DE是( )
A. 5 cm
B. 4 cm
C. 3 cm
D. 2 cm
下列关于等边三角形的描述错误的是( )
A. 三边相等的三角形是等边三角形
B. 三个角相等的三角形是等边三角形
C. 有一个角是60°的三角形是等边三角形
D. 有两个角是60°的三角形是等边三角形
下列说法正确的是( )
A. 等腰三角形的高、中线、角平分线互相重合
B. 顶角相等的两个等腰三角形全等
C. 等腰三角形一边不可以是另一边的三倍
D. 等腰三角形的两个底角相等
如图,在△ABC中,AB=AC,D为BC边上一点,且AD=AE,则∠BAD与∠EDC的关系为( )
A.∠BAD=∠EDC
B.∠BAD=2∠EDC
C.∠BAD+∠EDC=45°
D.∠BAD+∠EDC=60°
把分式的a、b、c的值都扩大为原来的3倍,则分式的值( )
A. 不变
B. 变为原来的3倍
C. 变为原来的
D. 变为原来的
下列是最简分式的是( )
A.
B.
C.
D.
小明骑自行车沿公路以akm/h的速度行走全程的一半,又以bkm/h的速度行走余下的一半路程;小刚骑自行车以akm/h的速度走全程时间的一半,又以bkm/h的速度行走另一半时间(a≠b),则谁走完全程所用的时间较少?( )
A. 小明
B. 小刚
C. 时间相同
D. 无法确定
二、填空题(本大题共6小题,共18分)
,,的最简公分母为 ______ .
计算:=____________.
若则 。
如图,点P是∠AOB的角平分线OC上一点,分别连接AP、BP,若再添加一个条件即可判定△AOP≌△BPO,则一下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC;④ AP=BP;⑤OA=OB.
其中一定正确的是 ______ (只需填序号即可)
如图,在△ABC中,AB=5cm,AC=3cm,BC的
垂直平分线分别交AB、BC于D、E,则△ACD的周长
为 ______ cm.
等腰三角形一腰上的高与另一腰的夹角为36°,则该等腰三角形的底角的度数为 ______ .
三、解答题(本大题共7个题,共55分)
19、计算(16分)
(1)
(2)
(3)
(4)
20、(6分)如图,点D在线段BC上,且AB=AD,BC=DE,AC=AE,∠1=42°,求∠3的度数.
21、(6分)先化简分式:然后在0、1、2、3中选一个你喜欢的数,代入求值。
22、(5分)尺规作图(保留作图痕迹,不写作法,) 如图,已知线段a,h,
求作:三角形ABC,使AC=BC,且AB=a,高CD=h。
23、(6分)如图,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,∠CAE:∠EAB=4:1,求∠B的度数. 24、(7分)如图,已知AD为等腰三角形ABC的底角的平分线,∠C=90°。有人说:AB=AC+CD,为什么?
25、(9分)如图:△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点,DE⊥DF. (1)∠1=∠2吗?为什么? (2)△ADE与△CDF全等吗?为什么? (3)若AB=8cm,求四边形AEDF的面积.
2017-2018学年第一学期期中考试八年级
数 学 答 案 卷
(时间:120分钟,满分:120分)
一、填空题(36′)
序号
1
2
3
4
5
6
7
8
9
10
11
12
选项
A
A
D
A
D
C
C
D
B
A
B
B
二、填空题(18′)
13、(x+y)(x-y) 14、 15、 6
16、 ①②③⑤ 17、 8 ㎝ 18、 63o或27o
三、解答题(16′+6′+6′+5′+6′+7′+9′)
19、计算(4分×4)
(1) (2)
(3) (4)
20、解:∵AD=AB,BC=DE,AC=AE
∴△ABC≌△ADE 2分
∴∠B=∠ADE 3分
又∵∠1+∠B+∠ADB=180o
∠3+∠ADE+∠ADB=180o 5分
∴∠3=∠1=42o 6分
21、先化简分式:然后在0、1、2、3中选一个你喜欢的数,代入求值。 解:
当m=2时,原式=2×2=4 (化简正确得3分,求值正确得6分)
22、作法:
△ABC就是所要作的三角形(弧线相交处各得1分,有结论得1分)
23、解:
∵DE是AB的垂直平分线
∴EA=EB
∴∠EAB=∠B 2分
又∵∠CAE∶∠EAB=4∶1
∴∠CAE∶∠B=4∶1
∴∠CAB=5∠B 4分
在Rt△ABC中,∠CAB+∠B=90o
得6∠B=90o
∴∠B=15o 6分
24、解:
作DE⊥AB,垂足为E, ∵△ABC是等腰直角三角形, ∴∠B=45°,又DE⊥AB, ∴DE=BE, 2分 ∵AD为△ABC的底角的平分线,∠C=90°,DE⊥AB, ∴DE=DC, 则CD=BE, 4分 在△CAD和△EAD中, , ∴△CAD≌△EAD, ∴AC=AE, ∴AB=AE+EB=AC+CD. 6分
25、解:(每一小题3分,酌情扣分)
(1)∵AB=AC,D是BC的中点
∴∠ADC=90o
∴∠2+∠ADF=90o
∵DE⊥DF
∴∠1+∠ADF=90o
∴∠1=∠2
(2) ∵△ABC是等腰直角三角形
∴∠C=45o
∵AB=AC,D是BC的中点
∴∠DAC=∠DAE=45o
∴DA=DC
在△ADE与△CDF中
∠EAD=∠C=45o DA=DC ∠1=∠2
∴△ADE≌△CDF
(3)由(2)△ADE≌△CDF
∴S△AED=S△CDF
∵S四边形AEDF=S△ADE+S△ADF
∴S四边形AEDF=S△CDF+S△ADF
=S△ADC
= S△ABC
=×8×8=16(㎝2)
(拙笨难免、仅供参考)
(时间:120分钟,满分:120分)
一、选择题(本大题共12小题,共36分)
如图,两个三角形为全等三角形,则∠α的度数是( )
A. 72°
B. 60°
C. 58°
D. 50°
如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
A. AC=BC+CE
B. ∠A=∠2
C. △ABC≌△CED
D. ∠A与∠D互余
下面四个图形分别是低碳、节水、节能和绿色食品标志,在这四个标志中,是轴对称图形的是( )
A.
B.
C.
D.
如图,如果直线m是多边形ABCDE的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )
A. 60°
B. 50°
C. 40°
D. 70°
到三角形的三个顶点距离相等的点是( )
A. 三条角平分线的交点
B. 三条中线的交点
C. 三条高的交点
D. 三条边的垂直平分线的交点
如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D.若CD=3cm,则点D到AB的距离DE是( )
A. 5 cm
B. 4 cm
C. 3 cm
D. 2 cm
下列关于等边三角形的描述错误的是( )
A. 三边相等的三角形是等边三角形
B. 三个角相等的三角形是等边三角形
C. 有一个角是60°的三角形是等边三角形
D. 有两个角是60°的三角形是等边三角形
下列说法正确的是( )
A. 等腰三角形的高、中线、角平分线互相重合
B. 顶角相等的两个等腰三角形全等
C. 等腰三角形一边不可以是另一边的三倍
D. 等腰三角形的两个底角相等
如图,在△ABC中,AB=AC,D为BC边上一点,且AD=AE,则∠BAD与∠EDC的关系为( )
A.∠BAD=∠EDC
B.∠BAD=2∠EDC
C.∠BAD+∠EDC=45°
D.∠BAD+∠EDC=60°
把分式的a、b、c的值都扩大为原来的3倍,则分式的值( )
A. 不变
B. 变为原来的3倍
C. 变为原来的
D. 变为原来的
下列是最简分式的是( )
A.
B.
C.
D.
小明骑自行车沿公路以akm/h的速度行走全程的一半,又以bkm/h的速度行走余下的一半路程;小刚骑自行车以akm/h的速度走全程时间的一半,又以bkm/h的速度行走另一半时间(a≠b),则谁走完全程所用的时间较少?( )
A. 小明
B. 小刚
C. 时间相同
D. 无法确定
二、填空题(本大题共6小题,共18分)
,,的最简公分母为 ______ .
计算:=____________.
若则 。
如图,点P是∠AOB的角平分线OC上一点,分别连接AP、BP,若再添加一个条件即可判定△AOP≌△BPO,则一下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC;④ AP=BP;⑤OA=OB.
其中一定正确的是 ______ (只需填序号即可)
如图,在△ABC中,AB=5cm,AC=3cm,BC的
垂直平分线分别交AB、BC于D、E,则△ACD的周长
为 ______ cm.
等腰三角形一腰上的高与另一腰的夹角为36°,则该等腰三角形的底角的度数为 ______ .
三、解答题(本大题共7个题,共55分)
19、计算(16分)
(1)
(2)
(3)
(4)
20、(6分)如图,点D在线段BC上,且AB=AD,BC=DE,AC=AE,∠1=42°,求∠3的度数.
21、(6分)先化简分式:然后在0、1、2、3中选一个你喜欢的数,代入求值。
22、(5分)尺规作图(保留作图痕迹,不写作法,) 如图,已知线段a,h,
求作:三角形ABC,使AC=BC,且AB=a,高CD=h。
23、(6分)如图,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,∠CAE:∠EAB=4:1,求∠B的度数. 24、(7分)如图,已知AD为等腰三角形ABC的底角的平分线,∠C=90°。有人说:AB=AC+CD,为什么?
25、(9分)如图:△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点,DE⊥DF. (1)∠1=∠2吗?为什么? (2)△ADE与△CDF全等吗?为什么? (3)若AB=8cm,求四边形AEDF的面积.
2017-2018学年第一学期期中考试八年级
数 学 答 案 卷
(时间:120分钟,满分:120分)
一、填空题(36′)
序号
1
2
3
4
5
6
7
8
9
10
11
12
选项
A
A
D
A
D
C
C
D
B
A
B
B
二、填空题(18′)
13、(x+y)(x-y) 14、 15、 6
16、 ①②③⑤ 17、 8 ㎝ 18、 63o或27o
三、解答题(16′+6′+6′+5′+6′+7′+9′)
19、计算(4分×4)
(1) (2)
(3) (4)
20、解:∵AD=AB,BC=DE,AC=AE
∴△ABC≌△ADE 2分
∴∠B=∠ADE 3分
又∵∠1+∠B+∠ADB=180o
∠3+∠ADE+∠ADB=180o 5分
∴∠3=∠1=42o 6分
21、先化简分式:然后在0、1、2、3中选一个你喜欢的数,代入求值。 解:
当m=2时,原式=2×2=4 (化简正确得3分,求值正确得6分)
22、作法:
△ABC就是所要作的三角形(弧线相交处各得1分,有结论得1分)
23、解:
∵DE是AB的垂直平分线
∴EA=EB
∴∠EAB=∠B 2分
又∵∠CAE∶∠EAB=4∶1
∴∠CAE∶∠B=4∶1
∴∠CAB=5∠B 4分
在Rt△ABC中,∠CAB+∠B=90o
得6∠B=90o
∴∠B=15o 6分
24、解:
作DE⊥AB,垂足为E, ∵△ABC是等腰直角三角形, ∴∠B=45°,又DE⊥AB, ∴DE=BE, 2分 ∵AD为△ABC的底角的平分线,∠C=90°,DE⊥AB, ∴DE=DC, 则CD=BE, 4分 在△CAD和△EAD中, , ∴△CAD≌△EAD, ∴AC=AE, ∴AB=AE+EB=AC+CD. 6分
25、解:(每一小题3分,酌情扣分)
(1)∵AB=AC,D是BC的中点
∴∠ADC=90o
∴∠2+∠ADF=90o
∵DE⊥DF
∴∠1+∠ADF=90o
∴∠1=∠2
(2) ∵△ABC是等腰直角三角形
∴∠C=45o
∵AB=AC,D是BC的中点
∴∠DAC=∠DAE=45o
∴DA=DC
在△ADE与△CDF中
∠EAD=∠C=45o DA=DC ∠1=∠2
∴△ADE≌△CDF
(3)由(2)△ADE≌△CDF
∴S△AED=S△CDF
∵S四边形AEDF=S△ADE+S△ADF
∴S四边形AEDF=S△CDF+S△ADF
=S△ADC
= S△ABC
=×8×8=16(㎝2)
(拙笨难免、仅供参考)
同课章节目录
