第11讲选修4-1《几何证明选讲》模块综合检测题Word版含解析
文档属性
| 名称 | 第11讲选修4-1《几何证明选讲》模块综合检测题Word版含解析 |
|
|
| 格式 | zip | ||
| 文件大小 | 465.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-24 15:07:33 | ||
图片预览




文档简介
选修4-1《几何证明选讲》模块综合检测题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
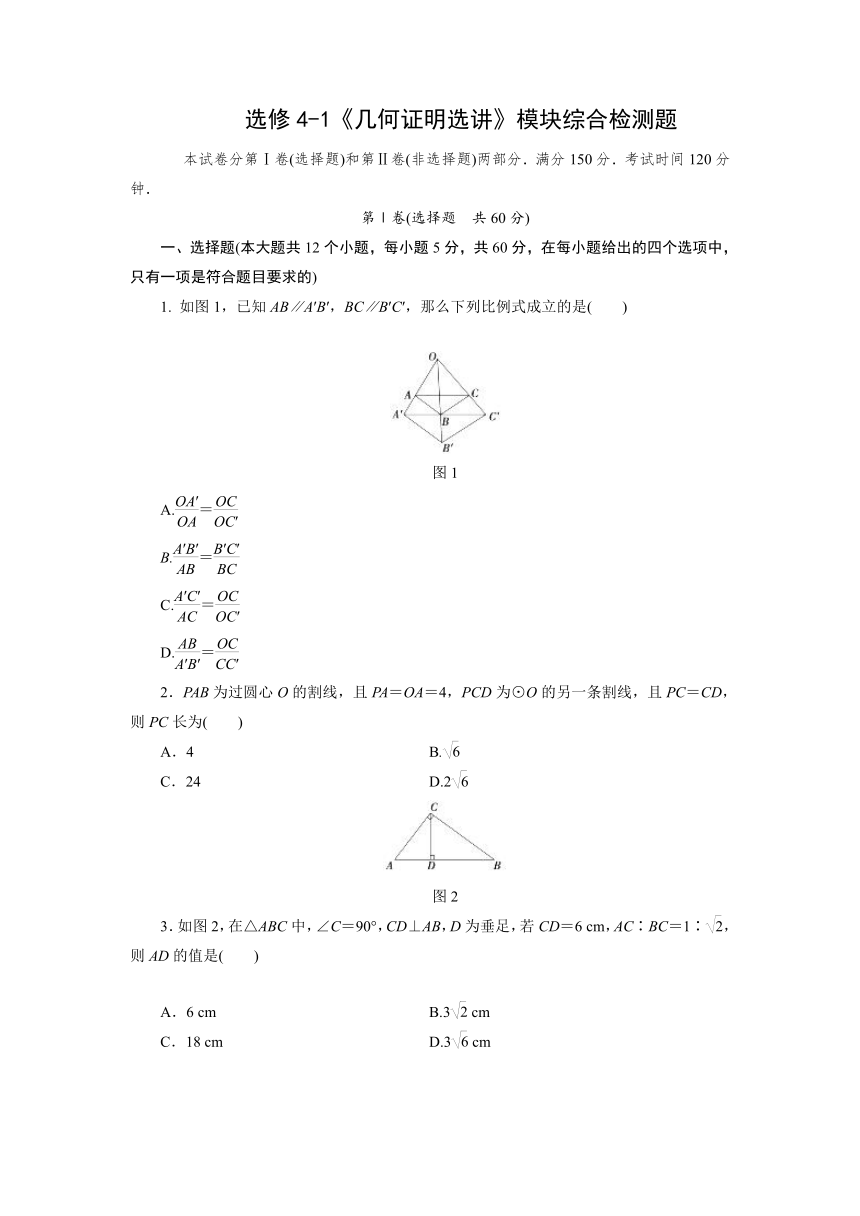
1. 如图1,已知AB∥A′B′,BC∥B′C′,那么下列比例式成立的是( )
图1
A.=
B.=
C.=
D.=
2.PAB为过圆心O的割线,且PA=OA=4,PCD为⊙O的另一条割线,且PC=CD,则PC长为( )
A.4 B.
C.24 D.2
图2
3.如图2,在△ABC中,∠C=90°,CD⊥AB,D为垂足,若CD=6 cm,AC∶BC=1∶,则AD的值是( )
A.6 cm B.3 cm
C.18 cm D.3 cm
图3
4.如图3,⊙O内切于△ABC,切点分别为D、E、F.已知∠B=50°,∠C=60°,连接OE、OF、DE、DF,那么∠EDF等于( )
A.40° B.55°
C.65° D.70°
图4
5.如图4,平行四边形ABCD中,AE∶EB=1∶2,若△AEF的面积等于2 cm2,则△CDF的面积等于( )
A.16 cm2 B.18 cm2
C.20 cm2 D.22 cm2
图5
6.如图7,点C在以AB为直径的半圆上,连接AC、BC,AB=10,tan∠BAC=,则阴影部分的面积为( )
A.π B.π-24
C.24 D.+24
图6
7.如图6,用与底面成30°角的平面截圆柱得一椭圆截线,则该椭圆的离心率为( )
A. B.
C. D.非上述结论
8.如图7所示,∠ACB=90°,CD⊥AB于点D,以BD为直径的圆与BC交于点E,则( )
图7
A.CE·CB=AD·DB
B.CE·CB=AD·AB
C.AD·AB=CD2
D.CE·EB=CD2
图8
9.如图8,AB、CD是圆O的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=2,则线段AC的长度为( )
A.5 B.
C. D.3
图9
10.如图9,E,C分别是∠A两边上的点,以CE为直径的⊙O交∠A的两边于点D,点B,若∠A=45°,则△AEC与△ADB的面积比为( )
A.2∶1 B.1∶2
C.∶1 D.∶1
11.
图10
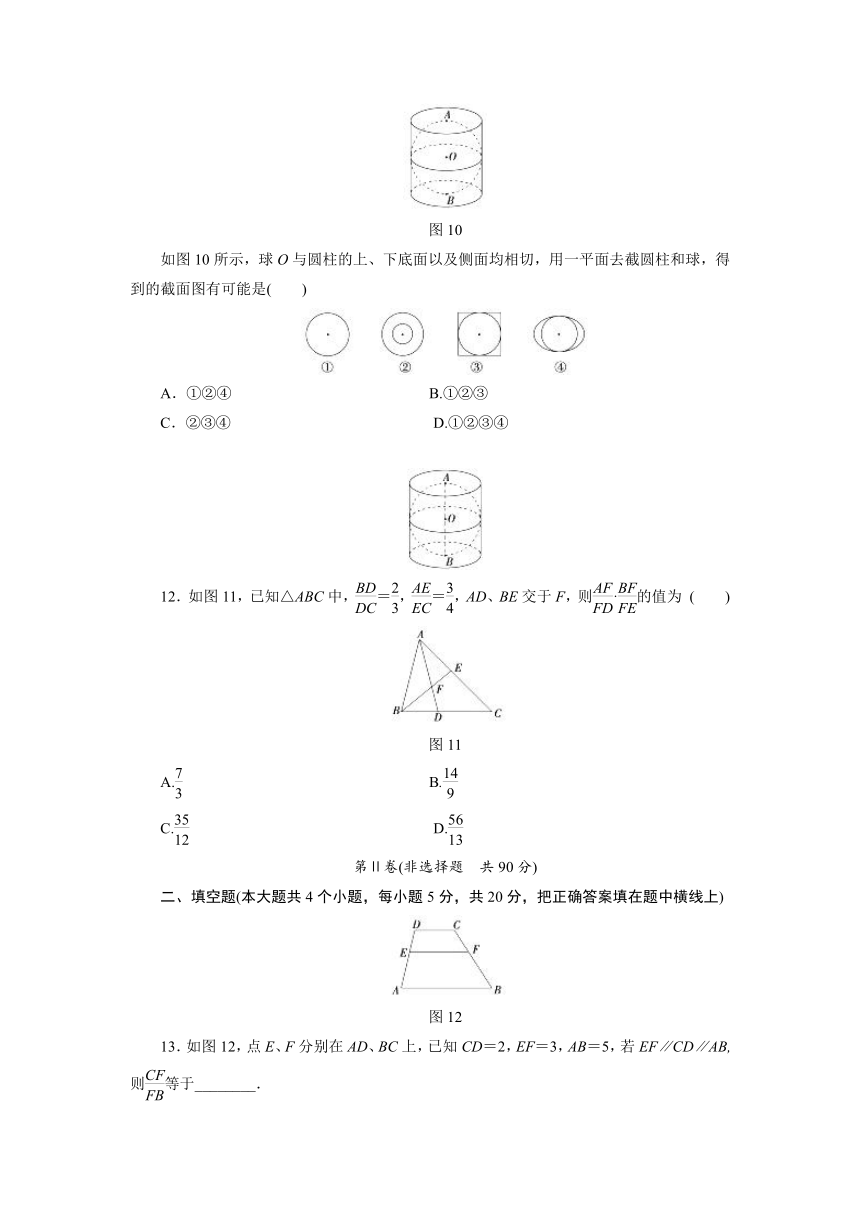
如图10所示,球O与圆柱的上、下底面以及侧面均相切,用一平面去截圆柱和球,得到的截面图有可能是( )
A.①②④ B.①②③
C.②③④ D.①②③④
12.如图11,已知△ABC中,=,=,AD、BE交于F,则·的值为 ( )
图11
A. B.
C. D.
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
图12
13.如图12,点E、F分别在AD、BC上,已知CD=2,EF=3,AB=5,若EF∥CD∥AB, 则等于________.
图13
14.如图13,PT切⊙O于点T,PA交⊙O于A、B两点,且与直径CT交于点D.CD=2,AD=3,BD=6,则PB=________.
15.一平面与半径为4的圆柱面相截,截面的Dandelin双球的球心距离为12,则截线椭圆的离心率e=________.
图14
16.已知如图14,△ABC中,边AC上一点F分AC为=,BF上一点G分BF为=,AG的延长线与BC交于点E,则BE∶EC=________.
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)已知如图15,DE∥BC,四边形DEFG是平行四边形.求证:AH∥DG.
图15
18.(本小题满分12分)如图16,AB为⊙O的直径,AD、BC是⊙O的切线,DC切⊙O于E,并与AD、BC分别交于D、C两点,BD与AC交于点F,求证:FE∥A D.
图16
19.(本小题满分12分)如图17,圆O1与圆O2内切于点A,其半径分别为r1与r2(r1>r2).圆O1的弦AB交圆O2于点C(O1不在AB上).求证:AB∶AC为定值.
图17
20.(本小题满分12分)如图18所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.
(1)求证:AD∥EC;
(2)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.
图18
21.(本小题满分12分)如图19,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧BC中点,连接AG分别交⊙O、BD于点E、F,连接CE.
求证:(1)AG·EF=CE·GD;
(2)=.
图19
22.(本小题满分12分)已知AD为圆O的直径,直线BA与圆O相切与点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.
(1)求证:BA·DC=GC·AD;
(2)求BM.
图20
选修4-1《几何证明选讲》模块综合检测题参考答案
选择题答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
B
B
B
B
A
A
C
A
D
C
【第1题解析】∵AB∥A′B′∴=.同理=.∴=,∴A不成立.
==,∴=,∴B成立由于=,∴AC∥A′C′∴=,∴C不成立.==,∴D不成立.故选B.
【第2题解析】由题意知PA·PB=PC·PD,设PC=x,则PD=2x,∴2x·x=4×12,∴x=2,即PC=2.故选D.
【第4题解析】∵∠B=50°,∠C=60°,∴∠A=70°,∴∠EOF=110°,∴∠EDF=55°.故选B.
【第5题解析】∵=,∴==,∵DC∥AE,∴△DCF∽△EAF,∴=()2=()2,即=9,∴S△DCF=18(cm2).故选B.
【第6题解析】∵AB为直径,∴∠ACB=90°.∵tan∠BAC=,∴sin∠BAC=.又∵sin∠BAC=,AB=10,∴BC=×10=6,AC=×BC=×6=8,∴S阴影=S半圆-S△ABC=×π×52-×8×6=π-24.故选B.
【第7题解析】用平面截圆柱,椭圆截线的短轴长为圆柱截面圆的直径,且椭圆所在平面与底面成30°角,则离心率e=sin 30°=.故选A.
【第8题解析】根据CD是Rt△ABC的斜边AB上的高及CD是圆的切线求解.在Rt△ABC中,∵∠ACB=90°,CD⊥AB,∴CD2=AD·DB.又CD是圆的切线,故CD2=CE·CB.∴CE·CB=AD·DB.故选A.
【第9题解析】连接BC,∵AB垂直平分CD,∴CP2=AP.PB.设PB=x,则AP=6-x.∴x(6-x)=5,∴x1=1,x2=5(由题图可知,不合题意,舍去).即AP=5,又CP==,∴AC==.故选C.
【第10题解析】连接BE,求△AEC与△ABD的面积比即求AE2∶AB2的值,设AB=a,∵∠A=45°,又∵CE为⊙O的直径,∴∠CBE=∠ABE=90°,∴BE=AB=a,∴AE=a,∴AE2∶AB2=2a2∶a2,即AE2∶AB2=2∶1,∴S△AEC∶S△ABD=2∶1.故选A.
【第11题解析】如图所示连接AB,AB为圆柱的轴,当平面与AB垂直且过AB中点时,截得图形是图①,当平面与AB垂直不过AB中点时,截得图形是两个同心圆,是图②,当平面经过轴AB时,截得的图形是图③,当平面与轴AB不垂直且平面与圆柱的侧面有交线时,截得的图形是图④,故有可能的图形是①②③④.故选D.学科*网
【第12题解析】过D作DG∥BE交AC于G.∵=,∴=.∴==.∴DG=BE.又==,∴EG=EC.又=,∴EC=AE.∴==
==.∴FE=DG=×BE=BE.∴=,==.
∴·=×=.故选C.
填空题答案
第13题
第14题
15
第15题
第16题
3∶5
【第13题解析】如图,过C作CH∥DA交EF于G,交AB于H,则EG=AH=DC=2,GF=1,BH=3.
∵GF∥HB,∴==,∴=.故填.
【第14题解析】∵AD·BD=CD·DT,∴DT=9,∴PT2=(PB+6)2-81.又∵PT2=PB·(PB+9),∴PB=15.故填15.
【第16题解析】过F作FD∥AE交BC于D,如图所示,则==,==,故CD=DE,BE=DE,EC=CD+DE=DE+DE=DE,从而=.故填3∶5.
【第17题答案】证明见解析
【第17题解析】∵DE∥BC,
∴=.
∵GF∥DE,∴GF∥BC,
∴=.
∵GF=DE,∴=,∴=.
∴AH∥DG.
【第18题答案】证明见解析
【第19题答案】见解析
【第19题解析】连接AO1,并延长分别交两圆于点E和点D.连接BD,CE.
因为圆O1与圆O2内切于点A,所以点O2在AD上.故AD,AE分别为圆O1,圆O2的直径.
从而∠ABD=∠ACE=.所以BD∥CE,
于是===.
所以AB∶AC为定值.
【第20题答案】(1)证明见解析;(2)AD=12.
【第20题解析】(1)证明:连接AB,
∵AC是⊙O1的切线,
∴∠BAC=∠D,
又∵∠BAC=∠E,∴∠D=∠E.
∴AD∥EC.
(2)设BP=x,PE=y,
∵PA=6,PC=2,∴xy=12,①
∵AD∥EC,∴=?=,②
由①②得,或(舍去)
∴DE=9+x+y=16,
∵AD是⊙O2的切线,
∴AD2=DB·DE=9×16,
∴AD=12.
【第21题答案】(1)证明见解析;(2)见解析.
∵G为弧BD的中点,∴∠DAG=∠GDF,
∴∠DAG=∠ECF,∴△CEF∽△AGD,
∴=,∴AG·EF=CE·GD.
(2)由(1)知∠DAG=∠GDF,∠G=∠G,
∴△DFG∽△ADG,
∴DG2=AG·GF,
由(1)知=,∴=.
【第22题答案】(1)证明见解析;(2)BM=5.
【第22题解析】 (1)证明:因为AC⊥OB,所以∠AGB=90°,
又AD是圆O的直径,所以∠DCA=90°,
又因为∠BAG=∠ADC(弦切角等于同弧所对圆周角)
所以△AGB∽△DCA,所以=,
又因为OG⊥AC,所以GC=AG,
所以=,即BA·DC=GC·AD.
(2)因为AC=12,所以AG=6,
因为AB=10,所以BG==8,
由(1)知:Rt△AGB∽Rt△DCA,所以=,
所以AD=15,即圆的直径2r=15,
又因为AB2=BM·(BM+2r),即BM2+15BM-100=0.
解得BM=5.
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 如图1,已知AB∥A′B′,BC∥B′C′,那么下列比例式成立的是( )
图1
A.=
B.=
C.=
D.=
2.PAB为过圆心O的割线,且PA=OA=4,PCD为⊙O的另一条割线,且PC=CD,则PC长为( )
A.4 B.
C.24 D.2
图2
3.如图2,在△ABC中,∠C=90°,CD⊥AB,D为垂足,若CD=6 cm,AC∶BC=1∶,则AD的值是( )
A.6 cm B.3 cm
C.18 cm D.3 cm
图3
4.如图3,⊙O内切于△ABC,切点分别为D、E、F.已知∠B=50°,∠C=60°,连接OE、OF、DE、DF,那么∠EDF等于( )
A.40° B.55°
C.65° D.70°
图4
5.如图4,平行四边形ABCD中,AE∶EB=1∶2,若△AEF的面积等于2 cm2,则△CDF的面积等于( )
A.16 cm2 B.18 cm2
C.20 cm2 D.22 cm2
图5
6.如图7,点C在以AB为直径的半圆上,连接AC、BC,AB=10,tan∠BAC=,则阴影部分的面积为( )
A.π B.π-24
C.24 D.+24
图6
7.如图6,用与底面成30°角的平面截圆柱得一椭圆截线,则该椭圆的离心率为( )
A. B.
C. D.非上述结论
8.如图7所示,∠ACB=90°,CD⊥AB于点D,以BD为直径的圆与BC交于点E,则( )
图7
A.CE·CB=AD·DB
B.CE·CB=AD·AB
C.AD·AB=CD2
D.CE·EB=CD2
图8
9.如图8,AB、CD是圆O的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=2,则线段AC的长度为( )
A.5 B.
C. D.3
图9
10.如图9,E,C分别是∠A两边上的点,以CE为直径的⊙O交∠A的两边于点D,点B,若∠A=45°,则△AEC与△ADB的面积比为( )
A.2∶1 B.1∶2
C.∶1 D.∶1
11.
图10
如图10所示,球O与圆柱的上、下底面以及侧面均相切,用一平面去截圆柱和球,得到的截面图有可能是( )
A.①②④ B.①②③
C.②③④ D.①②③④
12.如图11,已知△ABC中,=,=,AD、BE交于F,则·的值为 ( )
图11
A. B.
C. D.
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
图12
13.如图12,点E、F分别在AD、BC上,已知CD=2,EF=3,AB=5,若EF∥CD∥AB, 则等于________.
图13
14.如图13,PT切⊙O于点T,PA交⊙O于A、B两点,且与直径CT交于点D.CD=2,AD=3,BD=6,则PB=________.
15.一平面与半径为4的圆柱面相截,截面的Dandelin双球的球心距离为12,则截线椭圆的离心率e=________.
图14
16.已知如图14,△ABC中,边AC上一点F分AC为=,BF上一点G分BF为=,AG的延长线与BC交于点E,则BE∶EC=________.
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)已知如图15,DE∥BC,四边形DEFG是平行四边形.求证:AH∥DG.
图15
18.(本小题满分12分)如图16,AB为⊙O的直径,AD、BC是⊙O的切线,DC切⊙O于E,并与AD、BC分别交于D、C两点,BD与AC交于点F,求证:FE∥A D.
图16
19.(本小题满分12分)如图17,圆O1与圆O2内切于点A,其半径分别为r1与r2(r1>r2).圆O1的弦AB交圆O2于点C(O1不在AB上).求证:AB∶AC为定值.
图17
20.(本小题满分12分)如图18所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.
(1)求证:AD∥EC;
(2)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.
图18
21.(本小题满分12分)如图19,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧BC中点,连接AG分别交⊙O、BD于点E、F,连接CE.
求证:(1)AG·EF=CE·GD;
(2)=.
图19
22.(本小题满分12分)已知AD为圆O的直径,直线BA与圆O相切与点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.
(1)求证:BA·DC=GC·AD;
(2)求BM.
图20
选修4-1《几何证明选讲》模块综合检测题参考答案
选择题答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
B
B
B
B
A
A
C
A
D
C
【第1题解析】∵AB∥A′B′∴=.同理=.∴=,∴A不成立.
==,∴=,∴B成立由于=,∴AC∥A′C′∴=,∴C不成立.==,∴D不成立.故选B.
【第2题解析】由题意知PA·PB=PC·PD,设PC=x,则PD=2x,∴2x·x=4×12,∴x=2,即PC=2.故选D.
【第4题解析】∵∠B=50°,∠C=60°,∴∠A=70°,∴∠EOF=110°,∴∠EDF=55°.故选B.
【第5题解析】∵=,∴==,∵DC∥AE,∴△DCF∽△EAF,∴=()2=()2,即=9,∴S△DCF=18(cm2).故选B.
【第6题解析】∵AB为直径,∴∠ACB=90°.∵tan∠BAC=,∴sin∠BAC=.又∵sin∠BAC=,AB=10,∴BC=×10=6,AC=×BC=×6=8,∴S阴影=S半圆-S△ABC=×π×52-×8×6=π-24.故选B.
【第7题解析】用平面截圆柱,椭圆截线的短轴长为圆柱截面圆的直径,且椭圆所在平面与底面成30°角,则离心率e=sin 30°=.故选A.
【第8题解析】根据CD是Rt△ABC的斜边AB上的高及CD是圆的切线求解.在Rt△ABC中,∵∠ACB=90°,CD⊥AB,∴CD2=AD·DB.又CD是圆的切线,故CD2=CE·CB.∴CE·CB=AD·DB.故选A.
【第9题解析】连接BC,∵AB垂直平分CD,∴CP2=AP.PB.设PB=x,则AP=6-x.∴x(6-x)=5,∴x1=1,x2=5(由题图可知,不合题意,舍去).即AP=5,又CP==,∴AC==.故选C.
【第10题解析】连接BE,求△AEC与△ABD的面积比即求AE2∶AB2的值,设AB=a,∵∠A=45°,又∵CE为⊙O的直径,∴∠CBE=∠ABE=90°,∴BE=AB=a,∴AE=a,∴AE2∶AB2=2a2∶a2,即AE2∶AB2=2∶1,∴S△AEC∶S△ABD=2∶1.故选A.
【第11题解析】如图所示连接AB,AB为圆柱的轴,当平面与AB垂直且过AB中点时,截得图形是图①,当平面与AB垂直不过AB中点时,截得图形是两个同心圆,是图②,当平面经过轴AB时,截得的图形是图③,当平面与轴AB不垂直且平面与圆柱的侧面有交线时,截得的图形是图④,故有可能的图形是①②③④.故选D.学科*网
【第12题解析】过D作DG∥BE交AC于G.∵=,∴=.∴==.∴DG=BE.又==,∴EG=EC.又=,∴EC=AE.∴==
==.∴FE=DG=×BE=BE.∴=,==.
∴·=×=.故选C.
填空题答案
第13题
第14题
15
第15题
第16题
3∶5
【第13题解析】如图,过C作CH∥DA交EF于G,交AB于H,则EG=AH=DC=2,GF=1,BH=3.
∵GF∥HB,∴==,∴=.故填.
【第14题解析】∵AD·BD=CD·DT,∴DT=9,∴PT2=(PB+6)2-81.又∵PT2=PB·(PB+9),∴PB=15.故填15.
【第16题解析】过F作FD∥AE交BC于D,如图所示,则==,==,故CD=DE,BE=DE,EC=CD+DE=DE+DE=DE,从而=.故填3∶5.
【第17题答案】证明见解析
【第17题解析】∵DE∥BC,
∴=.
∵GF∥DE,∴GF∥BC,
∴=.
∵GF=DE,∴=,∴=.
∴AH∥DG.
【第18题答案】证明见解析
【第19题答案】见解析
【第19题解析】连接AO1,并延长分别交两圆于点E和点D.连接BD,CE.
因为圆O1与圆O2内切于点A,所以点O2在AD上.故AD,AE分别为圆O1,圆O2的直径.
从而∠ABD=∠ACE=.所以BD∥CE,
于是===.
所以AB∶AC为定值.
【第20题答案】(1)证明见解析;(2)AD=12.
【第20题解析】(1)证明:连接AB,
∵AC是⊙O1的切线,
∴∠BAC=∠D,
又∵∠BAC=∠E,∴∠D=∠E.
∴AD∥EC.
(2)设BP=x,PE=y,
∵PA=6,PC=2,∴xy=12,①
∵AD∥EC,∴=?=,②
由①②得,或(舍去)
∴DE=9+x+y=16,
∵AD是⊙O2的切线,
∴AD2=DB·DE=9×16,
∴AD=12.
【第21题答案】(1)证明见解析;(2)见解析.
∵G为弧BD的中点,∴∠DAG=∠GDF,
∴∠DAG=∠ECF,∴△CEF∽△AGD,
∴=,∴AG·EF=CE·GD.
(2)由(1)知∠DAG=∠GDF,∠G=∠G,
∴△DFG∽△ADG,
∴DG2=AG·GF,
由(1)知=,∴=.
【第22题答案】(1)证明见解析;(2)BM=5.
【第22题解析】 (1)证明:因为AC⊥OB,所以∠AGB=90°,
又AD是圆O的直径,所以∠DCA=90°,
又因为∠BAG=∠ADC(弦切角等于同弧所对圆周角)
所以△AGB∽△DCA,所以=,
又因为OG⊥AC,所以GC=AG,
所以=,即BA·DC=GC·AD.
(2)因为AC=12,所以AG=6,
因为AB=10,所以BG==8,
由(1)知:Rt△AGB∽Rt△DCA,所以=,
所以AD=15,即圆的直径2r=15,
又因为AB2=BM·(BM+2r),即BM2+15BM-100=0.
解得BM=5.
