第01章章末检测-2017-2018学年高二数学人教版(选修1-2)
文档属性
| 名称 | 第01章章末检测-2017-2018学年高二数学人教版(选修1-2) | 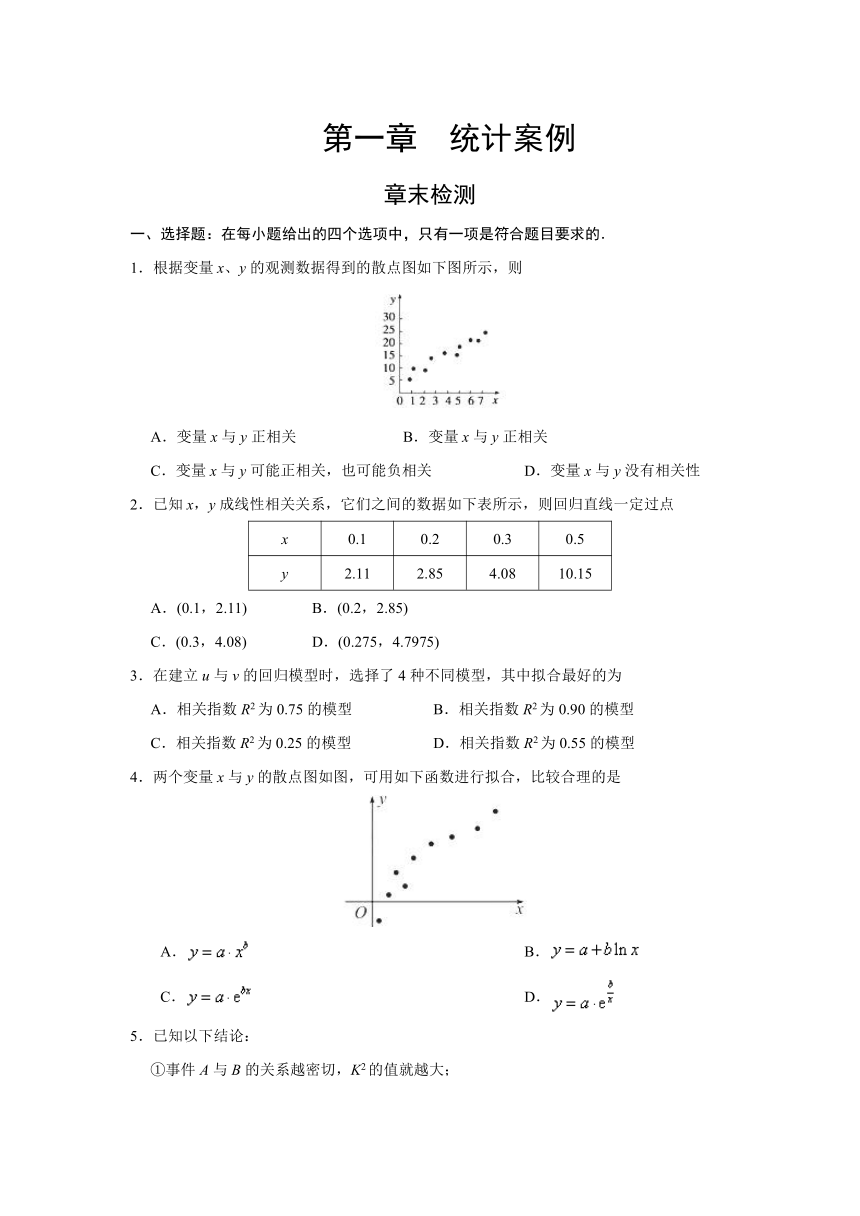 | |
| 格式 | zip | ||
| 文件大小 | 413.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-26 09:14:11 | ||
图片预览





文档简介
第一章 统计案例
章末检测
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.根据变量x、y的观测数据得到的散点图如下图所示,则
A.变量x与y正相关 B.变量x与y正相关
C.变量x与y可能正相关,也可能负相关 D.变量x与y没有相关性
2.已知x,y成线性相关关系,它们之间的数据如下表所示,则回归直线一定过点
x
0.1
0.2
0.3
0.5
y
2.11
2.85
4.08
10.15
A.(0.1,2.11) B.(0.2,2.85)
C.(0.3,4.08) D.(0.275,4.7975)
3.在建立u与v的回归模型时,选择了4种不同模型,其中拟合最好的为
A.相关指数R2为0.75的模型 B.相关指数R2为0.90的模型
C.相关指数R2为0.25的模型 D.相关指数R2为0.55的模型
4.两个变量x与y的散点图如图,可用如下函数进行拟合,比较合理的是
A. B.
C. D.
5.已知以下结论:
①事件A与B的关系越密切,K2的值就越大;
②K2的大小是判定事件A与B是否相关的唯一依据;
③若判定两事件A与B有关,则A发生B一定发生.
其中正确有
A.0个 B.1个
C.2个 D.3个
6.在新媒体时代,酒香也怕巷子深,宣传是让大众最快了解自己产品的最有效的手段,已知某种产品的宣传费用x与销售总额y的统计数据如下表所示:
宣传费用x万元
4
2
3
5
销售总额y万元
49
26
39
54
根据上表求得的回归方程中的为9.4,据此模型预报宣传费用为6万元时销售额为
A.63.6万元 B.65.5万元
C.67.7万元 D.72万元
7.“真人秀”热潮在我国愈演愈烈,为了了解学生是否喜欢某“真人秀”节目,在某中学随机调查了110名学生,得到如下列联表:
男
女
总计
喜欢
40
20
60
不喜欢
20
30
50
总计
60
50
110
由算得的观测值.
附表:
参照附表,得到的正确结论是
A.在犯错误的概率不超过0.1%的前提下,认为“喜欢该节目与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“喜欢该节目与性别无关”
C.有99%以上的把握认为“喜欢该节目与性别有关”
D.有99%以上的把握认为“喜欢该节目与性别无关”
8.考察棉花种子经过处理跟生病之间的关系得到如下表数据:
种子处理
种子未处理
合计
生病
32
101
133
不生病
61
213
274
合计
93
314
407
根据以上数据,则
A.种子是否经过处理跟是否生病有关 B.种子是否经过处理跟是否生病无关
C.种子是否经过处理决定是否生病 D.以上都是错误的
9.下表是性别与是否喜欢足球的统计列联表,依据表中的数据,可得到
喜欢足球
不喜欢足球
足球
男
40
28
68
女
5
12
17
总计
45
40
85
A.观测值 B.观测值
C.观测值 D.观测值
10.为了解高中生作文成绩与课外阅读量之间的关系,某研究机构随机抽取60名高中生做问卷调查,得到以下数据:
作文成绩优秀
作文成绩一般
总计
课外阅读量较大
22
10
32
课外阅读量一般
8
20
28
总计
30
30
60
则下说法正确的是
A.在样本数据中没有发现足够证据支持结论“作文成绩优秀与课外阅读量大有关”
B.在犯错误的概率不超过0.001的前提下认为“作文成绩优秀与课外阅读量大有关”
C.在犯错误的概率不超过0.05的前提下认为“作文成绩优秀与课外阅读量大有关”
D.在犯错误的概率不超过0.005的前提下认为“作文成绩优秀与课外阅读量大有关”
二、填空题:请将答案填在题中横线上.
11.若对于变量y与x的10组统计数据的回归模型中,相关指数,又知残差平方和为,那么______________.
12.如果由一个列联表中的数据计算得k=4.073,那么有______________的把握认为两变量有关系,已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025.
13.坚持可持续发展是需要我们长期坚守的基本战略,原料的循环利用是节省资源的有效方式之一.某化工厂为了预测某产品的回收率,需要研究它和原料有效成分含量之间的相关关系,现取了8对观测数据.计算知,,,,则y对x的回归方程是________________.
14.调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程为.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加______________万元.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
15.抽测了10名15岁男生的身高x(单位:cm)和体重y(单位:kg),得到如下数据:
x
157
153
151
158
156
159
160
158
160
162
y
45.5
44
42
46
44.5
45
46.5
47
45
49
(1)画出散点图;
(2)你能从散点图中发现身高与体重近似成什么关系吗?
(3)如果近似成线性关系,试画出一条直线来近似地表示这种关系.
16.在对人们休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动,能否判断性别与休闲方式是否有关系?
参考公式和数据:.
17.某班5名学生的数学和物理成绩如下表:
学生
学科
A
B
C
D
E
数学成绩(x)
88
76
73
66
63
物理成绩(y)
78
65
71
64
61
(1)画出散点图;
(2)求物理成绩y对数学成绩x的线性回归方程;
(3)一名学生的数学成绩是100分,试预测他的物理成绩(结果保留整数).
1.【答案】A
【解析】图中的数据y随x的增大而增大,因此变量x与y正相关,故选A.
2.【答案】D
【解析】回归直线一定过点,通过表格中的数据可计算出,,故选D.
3.【答案】B
【解析】相关指数R2的值越大,意味着残差平方和越小,也就是说模型的拟合效果越好,故选B.
4.【答案】B
【解析】由散点图知,此曲线类似对数型函数曲线,可用函数进行拟合.故选B.
6.【答案】B
【解析】由数据统计表可得,,根据回归直线的性质得点(3.5,42)在回归直线上,代入方程可得,故回归直线方程为,因此当x=6时,估计销售额万元.故选B.
7.【答案】C
【解析】由题中数据可得的观测值,所以99%以上的把握认为“喜欢该节目与性别有关”.故选C.
8.【答案】B
【解析】因为的观测值,所以可判断种子是否经过处理与是否生病无关,故选B.
9.【答案】D
【解析】由题可得的观测值
,故选D.
10.【答案】D
【解析】由题可得的观测值
,故在犯错误的概率不超过的前提下认为作文成绩优秀与课外阅读量大有关.故选D.
11.【答案】
【解析】依题意由,所以.
13.【答案】
【解析】由,,直接计算得,,所以.
14.【答案】
【解析】回归直线方程中字母b的意义为随着自变量增加或减少1个单位的函数值的变化量,即函数的平均变化率.本题中年收入每增加1万元,年饮食支出平均增加万元.
15.【答案】(1)见解析;(2)身高与体重线性相关;(3)见解析.
【解析】(1)散点图如下图所示:
(2)从散点图可知,当身高增加时,体重也增加,而且这些点在一条直线附近摆动,因此身高与体重线性相关.
(3)作出直线如图所示:
16.【答案】在犯错概率不超过0.025的前提下,认为休闲方式与性别有关.
【解析】建立列联表如下:
休闲方式为看电视
休闲方式为运动
合计
女性
43
27
70
男性
21
33
54
合计
64
60
124
17.【答案】(1)见解析;(2);(3)分.
【解析】(1)散点图如下图所示:
(2)由题可得,
,
,
.
所以,所以.
所以y对x的线性回归方程是.
章末检测
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.根据变量x、y的观测数据得到的散点图如下图所示,则
A.变量x与y正相关 B.变量x与y正相关
C.变量x与y可能正相关,也可能负相关 D.变量x与y没有相关性
2.已知x,y成线性相关关系,它们之间的数据如下表所示,则回归直线一定过点
x
0.1
0.2
0.3
0.5
y
2.11
2.85
4.08
10.15
A.(0.1,2.11) B.(0.2,2.85)
C.(0.3,4.08) D.(0.275,4.7975)
3.在建立u与v的回归模型时,选择了4种不同模型,其中拟合最好的为
A.相关指数R2为0.75的模型 B.相关指数R2为0.90的模型
C.相关指数R2为0.25的模型 D.相关指数R2为0.55的模型
4.两个变量x与y的散点图如图,可用如下函数进行拟合,比较合理的是
A. B.
C. D.
5.已知以下结论:
①事件A与B的关系越密切,K2的值就越大;
②K2的大小是判定事件A与B是否相关的唯一依据;
③若判定两事件A与B有关,则A发生B一定发生.
其中正确有
A.0个 B.1个
C.2个 D.3个
6.在新媒体时代,酒香也怕巷子深,宣传是让大众最快了解自己产品的最有效的手段,已知某种产品的宣传费用x与销售总额y的统计数据如下表所示:
宣传费用x万元
4
2
3
5
销售总额y万元
49
26
39
54
根据上表求得的回归方程中的为9.4,据此模型预报宣传费用为6万元时销售额为
A.63.6万元 B.65.5万元
C.67.7万元 D.72万元
7.“真人秀”热潮在我国愈演愈烈,为了了解学生是否喜欢某“真人秀”节目,在某中学随机调查了110名学生,得到如下列联表:
男
女
总计
喜欢
40
20
60
不喜欢
20
30
50
总计
60
50
110
由算得的观测值.
附表:
参照附表,得到的正确结论是
A.在犯错误的概率不超过0.1%的前提下,认为“喜欢该节目与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“喜欢该节目与性别无关”
C.有99%以上的把握认为“喜欢该节目与性别有关”
D.有99%以上的把握认为“喜欢该节目与性别无关”
8.考察棉花种子经过处理跟生病之间的关系得到如下表数据:
种子处理
种子未处理
合计
生病
32
101
133
不生病
61
213
274
合计
93
314
407
根据以上数据,则
A.种子是否经过处理跟是否生病有关 B.种子是否经过处理跟是否生病无关
C.种子是否经过处理决定是否生病 D.以上都是错误的
9.下表是性别与是否喜欢足球的统计列联表,依据表中的数据,可得到
喜欢足球
不喜欢足球
足球
男
40
28
68
女
5
12
17
总计
45
40
85
A.观测值 B.观测值
C.观测值 D.观测值
10.为了解高中生作文成绩与课外阅读量之间的关系,某研究机构随机抽取60名高中生做问卷调查,得到以下数据:
作文成绩优秀
作文成绩一般
总计
课外阅读量较大
22
10
32
课外阅读量一般
8
20
28
总计
30
30
60
则下说法正确的是
A.在样本数据中没有发现足够证据支持结论“作文成绩优秀与课外阅读量大有关”
B.在犯错误的概率不超过0.001的前提下认为“作文成绩优秀与课外阅读量大有关”
C.在犯错误的概率不超过0.05的前提下认为“作文成绩优秀与课外阅读量大有关”
D.在犯错误的概率不超过0.005的前提下认为“作文成绩优秀与课外阅读量大有关”
二、填空题:请将答案填在题中横线上.
11.若对于变量y与x的10组统计数据的回归模型中,相关指数,又知残差平方和为,那么______________.
12.如果由一个列联表中的数据计算得k=4.073,那么有______________的把握认为两变量有关系,已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025.
13.坚持可持续发展是需要我们长期坚守的基本战略,原料的循环利用是节省资源的有效方式之一.某化工厂为了预测某产品的回收率,需要研究它和原料有效成分含量之间的相关关系,现取了8对观测数据.计算知,,,,则y对x的回归方程是________________.
14.调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程为.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加______________万元.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
15.抽测了10名15岁男生的身高x(单位:cm)和体重y(单位:kg),得到如下数据:
x
157
153
151
158
156
159
160
158
160
162
y
45.5
44
42
46
44.5
45
46.5
47
45
49
(1)画出散点图;
(2)你能从散点图中发现身高与体重近似成什么关系吗?
(3)如果近似成线性关系,试画出一条直线来近似地表示这种关系.
16.在对人们休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动,能否判断性别与休闲方式是否有关系?
参考公式和数据:.
17.某班5名学生的数学和物理成绩如下表:
学生
学科
A
B
C
D
E
数学成绩(x)
88
76
73
66
63
物理成绩(y)
78
65
71
64
61
(1)画出散点图;
(2)求物理成绩y对数学成绩x的线性回归方程;
(3)一名学生的数学成绩是100分,试预测他的物理成绩(结果保留整数).
1.【答案】A
【解析】图中的数据y随x的增大而增大,因此变量x与y正相关,故选A.
2.【答案】D
【解析】回归直线一定过点,通过表格中的数据可计算出,,故选D.
3.【答案】B
【解析】相关指数R2的值越大,意味着残差平方和越小,也就是说模型的拟合效果越好,故选B.
4.【答案】B
【解析】由散点图知,此曲线类似对数型函数曲线,可用函数进行拟合.故选B.
6.【答案】B
【解析】由数据统计表可得,,根据回归直线的性质得点(3.5,42)在回归直线上,代入方程可得,故回归直线方程为,因此当x=6时,估计销售额万元.故选B.
7.【答案】C
【解析】由题中数据可得的观测值,所以99%以上的把握认为“喜欢该节目与性别有关”.故选C.
8.【答案】B
【解析】因为的观测值,所以可判断种子是否经过处理与是否生病无关,故选B.
9.【答案】D
【解析】由题可得的观测值
,故选D.
10.【答案】D
【解析】由题可得的观测值
,故在犯错误的概率不超过的前提下认为作文成绩优秀与课外阅读量大有关.故选D.
11.【答案】
【解析】依题意由,所以.
13.【答案】
【解析】由,,直接计算得,,所以.
14.【答案】
【解析】回归直线方程中字母b的意义为随着自变量增加或减少1个单位的函数值的变化量,即函数的平均变化率.本题中年收入每增加1万元,年饮食支出平均增加万元.
15.【答案】(1)见解析;(2)身高与体重线性相关;(3)见解析.
【解析】(1)散点图如下图所示:
(2)从散点图可知,当身高增加时,体重也增加,而且这些点在一条直线附近摆动,因此身高与体重线性相关.
(3)作出直线如图所示:
16.【答案】在犯错概率不超过0.025的前提下,认为休闲方式与性别有关.
【解析】建立列联表如下:
休闲方式为看电视
休闲方式为运动
合计
女性
43
27
70
男性
21
33
54
合计
64
60
124
17.【答案】(1)见解析;(2);(3)分.
【解析】(1)散点图如下图所示:
(2)由题可得,
,
,
.
所以,所以.
所以y对x的线性回归方程是.
