1.1 等腰三角形(1)同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
1.1等腰三角形（一）同步练习
姓名：__________班级：__________学号：__________
本节应掌握和应用的知识点
1.定理 等腰三角形的两底角相等.
2. 推论 等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合.
基础知识和能力拓展训练
1 、选择题
等腰三角形的一个角是80°，则它的底角是（　　）
A． 50° B． 80° C． 50°或80° D． 20°或80°
已知等腰三角形的一边长为4，另一边长为8，则这个等腰三角形的周长为（　　）
A．16 B．20或16 C．20 D．12
若等腰三角形有两条边的长度为3和1，则此等腰三角形的周长为（　　）
A．5 B．7 C．5或7 D．6
已知等腰三角形的两边长分别为6和5，则这个等腰三角形的周长是（　　）
A． 15或16 B． 16 C． 17 D． 16或17
若等腰三角形的顶角为80°，则它的底角度数为（　　）
A．80° B．50° C．40° D．20°
等腰三角形的一个角是50°，则它一腰上的高与底边的夹角是（ ）
A．25° B．40° C．25°或40° D．不能确定
从等腰三角形底边上任意一点，分别作两腰 ( http: / / www.21cnjy.com )的平行线，那么所构成的平行四边形的周长等于这个三角形的（ ）
A．周长的一半 B．周长 C．两腰的和 D．腰长
如图，△ABC中，AB=AC，BD=CD，下列说法不正确的是( )
( http: / / www.21cnjy.com / )
A．∠BAD= ( http: / / www.21cnjy.com / )∠BAC B．AD=BC C．∠B=∠C D．AD⊥BC
等腰三角形的一条边长为6，另一边长为13，则它的周长为（　　）
A．25 B．25或32 C．32 D．19
如图，在△ABC中，AB=AC，且D为BC上一点，CD=AD，AB=BD，则∠B的度数为（　　）
( http: / / www.21cnjy.com / )
A． 30° B． 36° C． 40° D． 45°
若在△ABC中，∠BAC的平分线交BC于D，AC=AB+BD，∠C=30°，则∠B的度数为（　　）
A．90° B．75° C．60° D．45°
2 、填空题
若（a﹣1）2+|b﹣2|=0，则以a、b为边长的等腰三角形的周长为　 　
已知一个等腰三角形的两边长分别为2和4，则该等腰三角形的周长是　　　　　　．
若等腰三角形的两边长分别为3cm和8cm，则它的周长是 。
等腰三角形的一内角等于50°，则其它两个内角各为_________________．
已知等腰三角形一腰上的中线把等腰三角形的周长分成9和12两部分，则等腰三角形的腰长为___________．21·cn·jy·com
已知：如图，△ABC中，AB=AC，BE∥AC，∠BDE=100°，∠BAD=70°，则∠E=　　　　　　．
( http: / / www.21cnjy.com / )
3 、解答题
如图，点D，E在△ABC的边BC上，AB=AC，BD=CE．求证：AD=AE．
( http: / / www.21cnjy.com / )
如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求∠A的度数．
( http: / / www.21cnjy.com / )
如图，在△ABC中，AB=AC，AD是BC边上的中线，BE⊥AC于点E．求证：∠CBE=∠BAD．
( http: / / www.21cnjy.com / )
求证：等腰三角形的两个底角相等
（请根据图用符号表示已知和求证，并写出证明过程）
已知：
求证：
证明：
( http: / / www.21cnjy.com / )
如图：已知在 ( http: / / www.21cnjy.com )中， ( http: / / www.21cnjy.com )， ( http: / / www.21cnjy.com )为 ( http: / / www.21cnjy.com )边的中点，过点 ( http: / / www.21cnjy.com )作 ( http: / / www.21cnjy.com )，垂足分别为 ( http: / / www.21cnjy.com ).求证： ( http: / / www.21cnjy.com )；
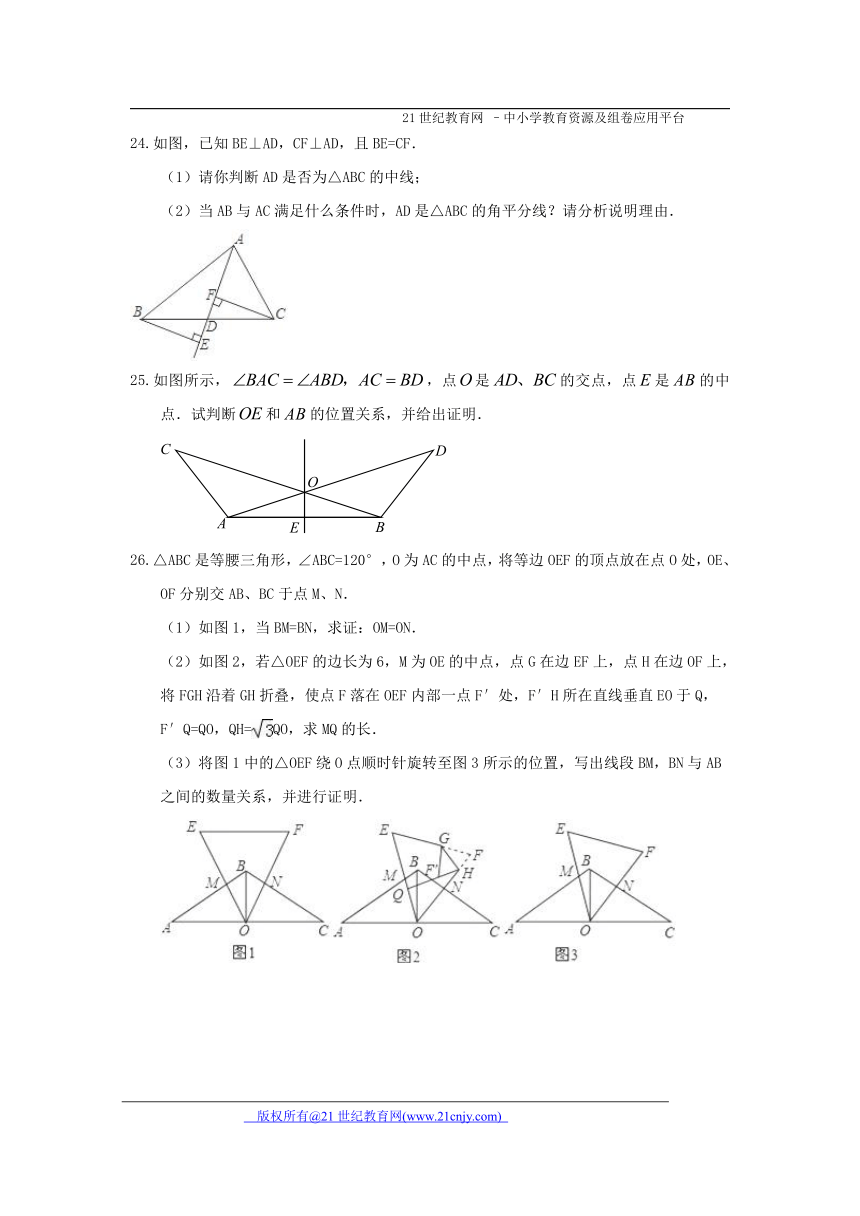
如图，已知BE⊥AD，CF⊥AD，且BE ( http: / / www.21cnjy.com )=CF．
（1）请你判断AD是否为△ABC的中线；
（2）当AB与AC满足什么条件时，AD是△ABC的角平分线？请分析说明理由．
( http: / / www.21cnjy.com / )
如图所示，，点是的交点，点是的中点．试判断和的位置关系，并给出证明．
△ABC是等腰三角形，∠ABC=120°，O为AC的中点，将等边OEF的顶点放在点O处，OE、OF分别交AB、BC于点M、N．21·世纪*教育网
（1）如图1，当BM=BN，求证：OM=ON．
（2）如图2，若△OEF的边长为6，M为OE的中点，点G在边EF上，点H在边OF上，将FGH沿着GH折叠，使点F落在OEF内部一点F′处，F′H所在直线垂直EO于Q，F′Q=QO，QH= ( http: / / www.21cnjy.com / )QO，求MQ的长．www-2-1-cnjy-com
（3）将图1中的△OEF绕O点顺时针旋转至图3所示的位置，写出线段BM，BN与AB之间的数量关系，并进行证明．2-1-c-n-j-y
( http: / / www.21cnjy.com / )
答案解析
1 、选择题
【分析】 因为题中没有指明该角是顶角还是底角，则应该分两种情况进行分析．
解：①当顶角是80°时，它的底角= ( http: / / www.21cnjy.com / )（180°﹣80°）=50°；
②底角是80°．
所以底角是50°或80°．
故选C．
【分析】分两种情况讨论解答
解：①当4为底时，其它两边都为8，
4、8、8可以构成三角形，
周长为20；
②当4为腰时，
其它两边为4和8，
∵4+4=8，
∴不能构成三角形，故舍去，
∴答案只有20．
故选C．
【分析】因为已知长度为3和1两边，没有明确是底边还是腰，所以有两种情况，需要分类讨论．
解：①当3为底时，其它两边都为1，
∵1+1＜3，
∴不能构成三角形，故舍去，
当3为腰时，
其它两边为3和1，
3、3、1可以构成三角形，
周长为7．
故选B．
【分析】 分6是腰长和底边两种情况，利用三角形的三边关系判断，然后根据三角形的周长的定义列式计算即可得解．【版权所有：21教育】
解：①6是腰长时，三角形的三边分别为6、6、5，
能组成三角形，
周长=6+6+5=17，
②6是底边时，三角形的三边分别为6、5、5，
能组成三角形，
周长=6+5+5=16，
综上所述，三角形的周长为16或17．
故选D．
点评： 本题考查了等腰三角形的性质，三角形的三边关系，难点在于分情况讨论．
【分析】根据等腰三角形两底角相等列式进行计算即可得解
解：∵等腰三角形的顶角为80°，
∴它的底角度数为（180°﹣80°）=50°．
故选B．
【分析】题中没有指明该角是顶角还是底角，则应该分情况进行分析，从而得到答案．
解：当底角是50°时，则它一腰上的高与底边的夹角是90°﹣50°=40°；
当顶角是50°时，则它的底角就是 ( http: / / www.21cnjy.com / )（180°﹣50°）=65°则它一腰上的高与底边的夹角是90°﹣65°=25°；【来源：21cnj*y.co*m】
故选C．
【分析】根据两直线平行，同位角相等与等 ( http: / / www.21cnjy.com )边对等角，易得∠1=∠B=∠2=∠C，根据等角对等边，即可得BE=DE，DF=CF，易得所成的平行四边形的周长等于这个等腰三角形的两腰的和．21教育名师原创作品
解：
∵AB=AC，
∴ ( http: / / www.21cnjy.com )∠B=∠C，
∵DE∥AC，DF∥AB，
∴∠1=∠C，∠2=∠B，
∴∠1=∠B，∠2=∠C，
∴BE=DE，DF=CF，
∴AE+DE+DF+AF=AE+BE+CF+AF=AB+AC．
∴所成的平行四边形的周长等于这个等腰三角形的两腰的和．
故选C．
( http: / / www.21cnjy.com / )
【分析】根据等腰三角形三线合一的性质，等边对等角的性质对各选项分析判断后利用排除法求解．
解：A．∵AB=AC，BD=CD，
∴∠BAD= ( http: / / www.21cnjy.com / )∠BAC，故本选项错误；
B、AD、BC的大小关系无法确定，故本选项正确；
C、∵AB=AC，
∴∠B=∠C，故本选项错误；
D、∵AB=AC，BD=CD，
∴AD⊥BC，故本选项错误．
故选B．
【分析】因为已知长度为6和13两边,没有明确是底边还是腰,所以有两种情况,需要分类讨论.
解：①当6为底时，其它两边都为13，
6、13、13可以构成三角形，
周长为32；
②当6为腰时，
其它两边为6和13，
∵6+6＜13，
∴不能构成三角形，故舍去，
∴答案只有32．
故选C．
【分析】 求出∠BAD=2∠CAD=2∠B=2∠C的关系，利用三角形的内角和是180°，求∠B，
解：∵AB=AC，
∴∠B=∠C，
∵AB=BD，
∴∠BAD=∠BDA，
∵CD=AD，
∴∠C=∠CAD，
∵∠BAD+∠CAD+∠B+∠C=180°，
∴5∠B=180°，
∴∠B=36°
故选：B．
【分析】利用三角形全等的性质计算．根 ( http: / / www.21cnjy.com )据已知条件中，两条线段的和等于其中一条线段，可以采用延长短线段或在长线段上截取的方法．综合运用了全等三角形的判定和性质；等腰三角形的性质以及三角形的外角的性质．21*cnjy*com
解：延长AB至E，使BE=BD，
又AC=AB+BD，
∴AE=AC，
在△ADE和△ADC中，
AD=AD，∠EAD=∠CAD，AE=AC，
∴△ADE≌△ADC，
∴∠E=∠C=30°，
∴∠BDE=∠E=30°，
∴∠ABD=∠E+∠BDE=60°．
故选C．
( http: / / www.21cnjy.com / )
2 、填空题
解：根据题意得，a﹣1=0，b﹣2=0，
解得a=1，b=2，
①若a=1是腰长，则底边为2，三角形的三边分别为1、1、2，
∵1+1=2，
∴不能组成三角形，
②若a=2是腰长，则底边为1，三角形的三边分别为2、2、1，
能组成三角形，
周长=2+2+1=5．
故答案为：5．
【分析】根据任意两边之和大于第三边，知道等腰三角形的腰的长度是4，底边长2，把三条边的长度加起来就是它的周长．www.21-cn-jy.com
解：因为2+2＜4，
所以等腰三角形的腰的长度是4，底边长2，
周长：4+4+2=10，
答：它的周长是10，
故答案为：10
【分析】已知没有明确腰和底边的 ( http: / / www.21cnjy.com )题目,要分类两种情况进行讨论：①8cm为腰，3cm为底，此时周长为19cm；②8cm为底，3cm为腰，则两边和小于第三边无法构成三角形，故舍去．所以它的其周长是19cm．21教育网
解：①8cm为腰，3cm为底时，周长=19cm;
②8cm为底，3cm为腰时，3+3＜8，故舍去
∴周长是19cm．
【分析】已知给出了一个内角是50°，没有明确是顶角还是底角，所以要进行分类讨论，分类后还有用内角和定理去验证每种情况是不是都成立．【出处：21教育名师】
解：当50°的角为底角时，只一个底角也为50°，顶角=180°﹣2×50×=80°；
当50°的角为顶角时，底角=（180°﹣50°）÷2=65°．
故答案为：50°，80°或65°，65°．
【分析】已知条件中未具体指明等腰 ( http: / / www.21cnjy.com )三角形一腰上的中线把等腰三角形周长分成的哪两部分的大小，从题意上看，故只考虑一部分长度为9（或12）时，会掉进命题“陷阱”，出现漏解现象．所以此问题应分为一部分长度为9 和12两种情形，
解：如图所示，即（1）当+=12、+=9时，解得=8、=5；（2）当+=9、+=12时，解得=6、=9．所以它的腰长为8或6．
故答案为：8或6．
( http: / / www.21cnjy.com / )
【分析】利用三角形的外角和定理求得∠ABC ( http: / / www.21cnjy.com )的度数，然后根据等腰三角形的性质，以及三角形的内角和定理求得∠BAC的度数，则∠CAD的度数即可得到，然后根据平行线的性质求得∠E的度数．21*cnjy*com
解：∵∠BDE=∠ABC+∠BAD，
∴∠ABC=∠BDE﹣∠BAD=100°﹣70°=30°，
∵AB=AC，
∴∠ABC=∠C=30°，
∴∠BAC=180°﹣∠ABC﹣∠C=120°，
∴∠CAD=∠BAC﹣∠BAD=120°﹣70°=50°，
∵BE∥AC，
∴∠E=∠CAD=50°．
故答案是：50°．
3 、解答题
【分析】利用等腰三角形的性质得到∠B=∠C，然后证明△ABD≌△ACE即可证得结论．
证明：∵AB=AC，
∴∠B=∠C，
在△ABD与△ACE中，
∵ ( http: / / www.21cnjy.com / )，
∴△ABD≌△ACE（SAS），
∴AD=AE．
【分析】由已知条件开始，通过线段相等，得到角相等，再由三角形内角和求出各个角的大小．
解：设∠A=x°．
∵BD=AD，
∴∠A=∠ABD=x°，
∠BDC=∠A+∠ABD=2x°，
∵BD=BC，
∴∠BDC=∠BCD=2x°，
∵AB=AC，
∴∠ABC=∠BCD=2x°，
在△ABC中x+2x+2x=180，
解得：x=36，
∴∠A=36°．
【分析】根据三角形三线 ( http: / / www.21cnjy.com )合一的性质可得∠CAD=∠BAD，根据同角的余角相等可得：∠CBE=∠CAD，再根据等量关系得到∠CBE=∠BAD．21世纪教育网版权所有
证明：∵AB=AC，AD是BC边上的中线，BE⊥AC，
∴∠CBE+∠C=∠CAD+∠C=90°，∠CAD=∠BAD，
∴∠CBE=∠BAD．
【分析】充分理解题意，利用等腰三角形的性质，要根据题意画图，添加辅助线来证明结论．
解：已知：△ABC中，AB=AC，
求证：∠B=∠C；
证明：如图，过D作BC⊥AD，垂足为点D，
∵AB=AC，AD=AD，
在Rt△ABD与Rt△ACD中， ( http: / / www.21cnjy.com / )，
∴Rt△ABD≌Rt△ACD（HL）
∴∠B=∠C．
( http: / / www.21cnjy.com / )
解：连接AD
∵，为边的中点
∴AD平分∠BAC
，
∴DE=DF
，
，
，
是的中点，
，
.
【分析】（1）求出∠BED=∠CFD，根据AAS证出△BED≌△CFD即可；
（2）根据等腰三角形的性质三线合一定理求出即可．
解：（1）∵BE⊥AD，CF⊥AD，
∴∠CFD=∠BED=90°，
在△BED和△CFD中
( http: / / www.21cnjy.com / )
∴△BED≌△CFD（AAS），
∴BD=DC，
即AD是△ABC的中线．2·1·c·n·j·y
（2）当AB=AC时，AD为△ABC的角平分线，
理由是：∵AB=AC，AD为△ABC的中线，
∴AD为△ABC的角平分线．【来源：21·世纪·教育·网】
解：通过所给条件可以证出
，得出，利用三线合一即可
解： ．
证明：在和中，
．
，
．
又．
【分析】（1）根据题意，可求得∠A=∠C，AO=CO，BM=BN，根据全等三角形的判定，即可证明△AOM≌△CON，则结论得证；
（2）根据Rt△OHQ中，∠EOF=60°，可用含OQ的式子表示出OH，即可表示出FH，根据 ( http: / / www.21cnjy.com / )，F′Q=OQ，用含OQ的式子表示出F′H，根据题意，可知FH=F′H，列出方程，即可求得OQ，则可求得MQ；
（3）取AB得中点G，连 ( http: / / www.21cnjy.com )接OG，根据直角三角形的中线定理，及30°的直角三角形的性质，证得OQ=OB，根据∠GOB=∠MON=60°，证得∠GOM=∠NOB，根据全等三角形的判定，即可证明GM=BN，即可证得BM、BN、AB的关系．
（1）证明：∵△ABC是等腰三角形，O是中点，
∴∠A=∠C，AO=CO，AB=BC，
又∵BM=BN，
∴AB﹣BM=BC﹣BN，
即AM=CN，
在△AOM和△CON中，
( http: / / www.21cnjy.com / )，
∴△AOM≌△CON，
∴OM=ON；
（2）解：∵△FGH沿着GH折叠得到△F′GH，
∴F′H=FH，
∵HQ⊥OM，
∴∠HQO=90°，
∵△OEF是等边三角形，
∴∠EOF=60°，
在Rt△OQH中，∠EOF=60°，
∴OH= ( http: / / www.21cnjy.com / )=2OQ，
∵OH= ( http: / / www.21cnjy.com / )OQ，F′Q=OQ，
∴F′H= ( http: / / www.21cnjy.com / )OQ﹣OQ=（ ( http: / / www.21cnjy.com / )﹣1）OQ，
∵OF=6，FH=6﹣2OQ，
∴（ ( http: / / www.21cnjy.com / )﹣1）OQ=6﹣2OQ，
解得：OQ=3 ( http: / / www.21cnjy.com / )﹣3，
∵OE=6，M是OE的中点，
∴OM=3，
∴MQ=MO﹣OQ=3﹣（3 ( http: / / www.21cnjy.com / )﹣3）=6﹣3 ( http: / / www.21cnjy.com / )；
（3）BM+BN= ( http: / / www.21cnjy.com / )AB；
证明如下：如右图，取AB的中点G，连接OG，则OG=AG=BG，
∵△ABC是等腰三角形，∠ABC=120°，O是AC的中点，
∴∠A=30°，∠ABO= ( http: / / www.21cnjy.com / )∠ABC=60°，
在△AOB中，∠A=30°，
∴OB=AG=BG，
∴OG=OB，∠GOB=60°，即∠1+∠2=60°，
由等边△EOF，得：∠EOF=60°，即∠2+∠3=60°，
∴∠1=∠3，
在△OGM和△OBN中
( http: / / www.21cnjy.com / )，
∴△OGM≌△OBN（ASA），
∴GM=BN，
∴BM+BN=BM+GM= ( http: / / www.21cnjy.com / )AB．
( http: / / www.21cnjy.com / )
【点评】本题主要考查了全等三角形的性质 ( http: / / www.21cnjy.com )和判定、等腰三角形的性质、勾股定理的综合应用，第（2）小题，用含有OQ的式子表示FH和F′H是解决本小题的关键；第（3）小题，解题的关键是将线段BM、BN，转化到线段AB上．21cnjy.com
( http: / / www.21cnjy.com / )
D
C
B
E
A
F
C
O
E
A
B
D
版权所有@21世纪教育网(www.21cnjy.com)