1.1 等腰三角形(2)同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
1.1等腰三角形的判定 同步练习
姓名：__________班级：__________学号：__________
本节应掌握和应用的知识点
1. 定理 有两个角相等的三角形是等腰三角形.
2.等腰三角形判定的应用
基础知识和能力拓展训练
一 、选择题
在下列四个角的度数中，一个不等边三角形的最小角度数可以是（　　）
A． 80° B． 65° C． 60° D． 59°
一个正方形和两个等边三角形的位置如图所示，若∠1=50°，则∠2+∠3=（　　）
( http: / / www.21cnjy.com / )
A． 190° B． 130° C． 100° D． 80°
在△ABC中，AB=AC，两底角平分线分别与AB、AC交于点D、E，图中等腰三角形的个数是（ ）
( http: / / www.21cnjy.com / )21世纪教育网版权所有
A． 2 B. 3 C. 4 D. 6【来源：21·世纪·教育·网】
推理：如图，∵∠A=∠ACD，∠B=∠BCD，（已知）∴AD=CD，CD=DB（ 等腰三角形的性质）∴AD=DB，依据是（ ） 21教育名师原创作品
( http: / / www.21cnjy.com / )
A． 旋转不改变图形的大小 B． 连接两点的所有线中线段最短
C． 等量代换 D． 整体大于部分
如图，在△ABC中，AB=AC，AD平 ( http: / / www.21cnjy.com )分∠BAC，DE⊥AB，DF⊥AC，E、F为垂足，则下列四个结论：（1）∠DEF=∠DFE；（2）AE=AF；（3）AD平分∠EDF；（4）EF垂直平分AD．其中正确的有（　　）
( http: / / www.21cnjy.com / )
A．1个 B．2个 C．3个 D．4个
如图，在下列三角形中，若AB＝AC ， 则能被一条直线分成两个小等腰三角形的是( )
( http: / / www.21cnjy.com / )
A．①②③ B.①②④ C.②③④ D.①③④
等边三角形的边长为2，则该三角形的面积为（　　）
A． ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / ) C. ( http: / / www.21cnjy.com / ) D.3
如图，△ABC中BD、CD平分∠ABC、 ( http: / / www.21cnjy.com )∠ACB，过D作直线平行于BC，交AB、AC于E、F，AB=5，AC=7，BC=8，△AEF的周长为（　　）【版权所有：21教育】
( http: / / www.21cnjy.com / )
A．13 B．12 C．15 D．20
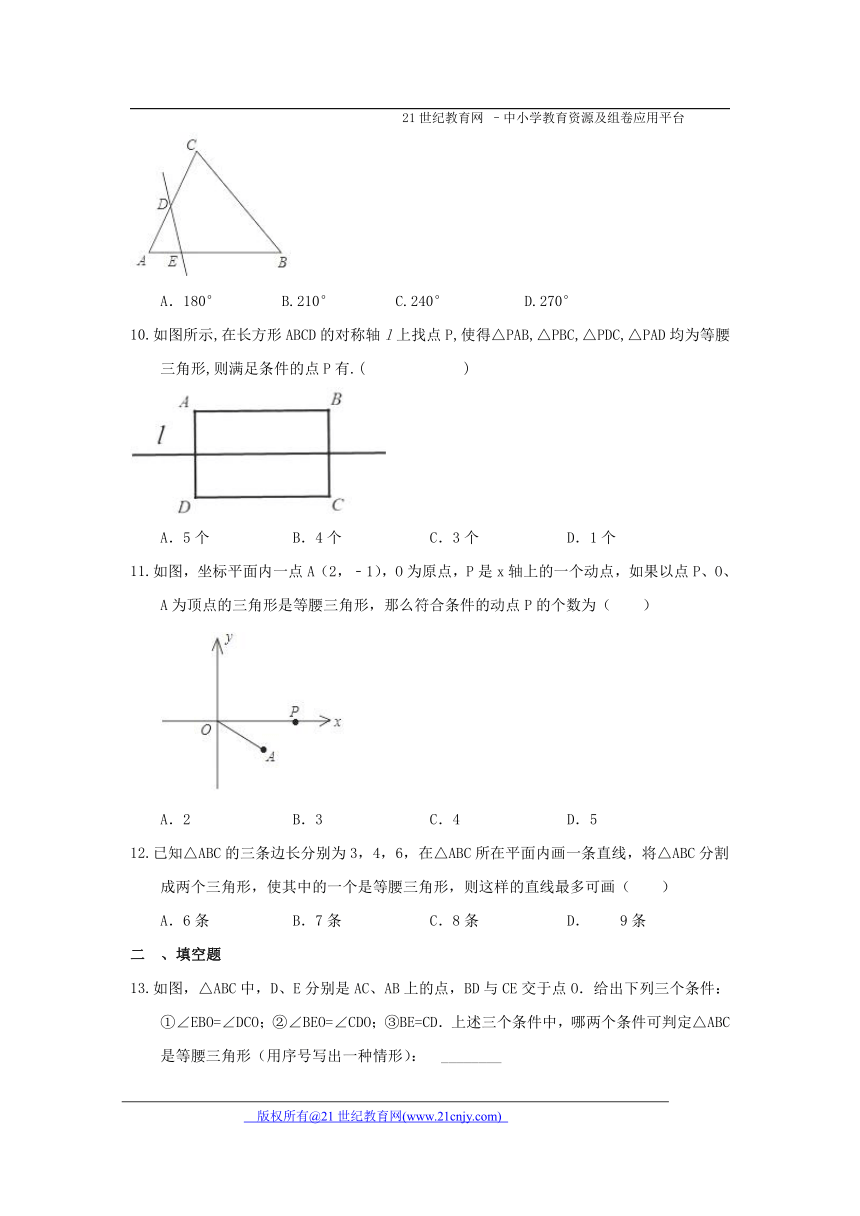
已知直线DE与不等边△ABC的两边AC，AB分别交于点D，E，若∠CAB=60°，则图中∠CDE+∠BED=（　　）
( http: / / www.21cnjy.com / )
A．180° B.210° C.240° D.270°
如图所示,在长方形ABCD的对称轴l上找 ( http: / / www.21cnjy.com )点P,使得△PAB,△PBC,△PDC,△PAD均为等腰三角形,则满足条件的点P有.( )21*cnjy*com
( http: / / www.21cnjy.com / )
A．5个 B．4个 C．3个 D．1个
如图，坐标平面内一点A（ ( http: / / www.21cnjy.com )2，﹣1），O为原点，P是x轴上的一个动点，如果以点P、O、A为顶点的三角形是等腰三角形，那么符合条件的动点P的个数为（ ）
( http: / / www.21cnjy.com / )
A．2 B．3 C．4 D．5
已知△ABC的三条边长分别为3，4， ( http: / / www.21cnjy.com )6，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（　　）
A．6条 B．7条 C．8条 D． 9条
二 、填空题
如图，△ABC中，D、E分别是A ( http: / / www.21cnjy.com )C、AB上的点，BD与CE交于点O．给出下列三个条件：①∠EBO=∠DCO；②∠BEO=∠CDO；③BE=CD．上述三个条件中，哪两个条件可判定△ABC是等腰三角形（用序号写出一种情形）： ________21cnjy.com
( http: / / www.21cnjy.com / )
如图，在3×3的网格中，每个网格 ( http: / / www.21cnjy.com )线的交点称为格点．已知图中A，B两个格点，请在图中再寻找另一个格点C，使△ABC成为等腰三角形，则满足条件的点C有　________ 　个．
( http: / / www.21cnjy.com / )
如图，在△ABC中，AB=AC，∠BAC=50°，D是BC边的中点，连接AD，则∠BAD=________．
( http: / / www.21cnjy.com / )
如图，△ABC中，D、E分别是AC、AB上 ( http: / / www.21cnjy.com )的点，BD与CE交于点O．给出下列三个条件：①∠EBO=∠DCO；②∠BEO=∠CDO；③BE=CD．上述三个条件中，哪两个条件可判定△ABC是等腰三角形（用序号写出一种情形）：________．
( http: / / www.21cnjy.com / )
在平面直角坐标系中，已知 ( http: / / www.21cnjy.com )点A（0，3）和点B（4，0）．若点C在x轴上，且在B的左侧，若以A．B、C三点为顶点的三角形是等腰三角形，则点C的坐标为________．
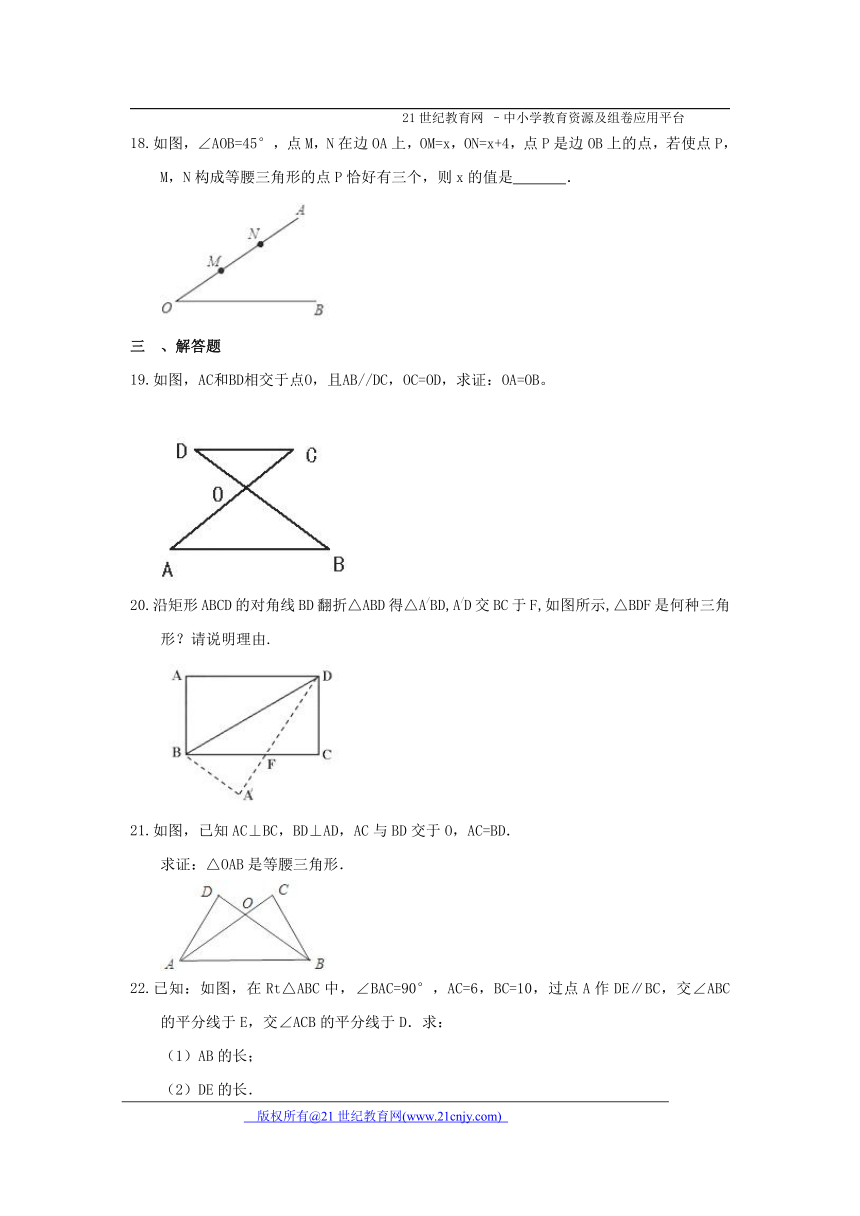
如图，∠AOB=45° ( http: / / www.21cnjy.com )，点M，N在边OA上，OM=x，ON=x+4，点P是边OB上的点，若使点P，M，N构成等腰三角形的点P恰好有三个，则x的值是　 　．
( http: / / www.21cnjy.com / )
三 、解答题
如图，AC和BD相交于点O，且AB//DC，OC=OD，求证：OA=OB。
( http: / / www.21cnjy.com / )
沿矩形ABCD的对角线BD翻折△ABD得△A/BD,A/D交BC于F,如图所示,△BDF是何种三角形？请说明理由.
( http: / / www.21cnjy.com / )
如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．
求证：△OAB是等腰三角形．
( http: / / www.21cnjy.com / )
已知：如图，在Rt△ABC中，∠BA ( http: / / www.21cnjy.com )C=90°，AC=6，BC=10，过点A作DE∥BC，交∠ABC的平分线于E，交∠ACB的平分线于D．求：
（1）AB的长；
（2）DE的长．
( http: / / www.21cnjy.com / )
如图，E在△ABC的AC边的延长线上 ( http: / / www.21cnjy.com )，D点在AB边上，DE交BC于点F，DF＝EF，BD＝CE.求证：△ABC是等腰三角形．(过D作DG∥AC交BC于G)．
( http: / / www.21cnjy.com / )
在△ABC中，AB＝AC，AB的中垂线与AC所在直线相交所得的锐角为50°，求底角B的大小．
数学课上，李老师出示了如下框中的题目．
( http: / / www.21cnjy.com / )
小敏与同桌小聪讨论后，进行了如下
（1）特殊情况，探索结论
当点E为AB的中点时，如图1，确定线段AE与DB的大小关系，请你直接写出结论：
AE　　DB（填“＞”，“＜”或“=”）．
( http: / / www.21cnjy.com / )
（2）特例启发，解答题目
解：题目中，AE与DB的大小关系是 ( http: / / www.21cnjy.com )：AE　　DB（填“＞”，“＜”或“=”）．理由如下：如图2，过点E作EF∥BC，交AC于点F．（请你完成以下解答过程）
在等腰直角三角形AOB中，已知AO⊥OB，点P、D分别在AB、OB上，
（1）如图1中，若PO=PD，∠OPD=45°，证明△BOP是等腰三角形．
（2）如图2中，若AB=10，点P在AB ( http: / / www.21cnjy.com )上移动，且满足PO=PD，DE⊥AB于点E，试问：此时PE的长度是否变化？若变化，说明理由；若不变，请予以证明．
( http: / / www.21cnjy.com / )
答案解析
一 、选择题
【分析】根据三角形的三角形的内角和等于180°求出最小的角的度数的取值范围，然后选择即可．　
解：180°÷3=60°，
∵不等边三角形的最小内角为∠A，
∴∠A＜60°，
∴0°＜∠A＜60°，
纵观各选项，∠A最大可取59°．
故选D
【分析】设围成的小三角形为△ABC，分别用∠1、∠2、∠3表示出△ABC的三个内角，再利用三角形的内角和等于180°列式整理即可得解．　21*cnjy*com
解：如图，∠BAC=180°﹣90°﹣∠1=90°﹣∠1，
∠ABC=180°﹣60°﹣∠3=120°﹣∠3，
∠ACB=180°﹣60°﹣∠2=120°﹣∠2，
在△ABC中，∠BAC+∠ABC+∠ACB=180°，
∴90°﹣∠1+120°﹣∠3+120°﹣∠2=180°，
∴∠1+∠2=150°﹣∠3，
∵∠1=50°，
∴∠2+∠3=150°﹣50°=100°．
故选C．
( http: / / www.21cnjy.com / )
【分析】根据等腰三角形的判定定理（ ( http: / / www.21cnjy.com )在同一三角形中，有两条边相等的三角形是等腰三角形；在同一三角形中，有两个角相等的三角形是等腰三角形）来证明图中的等腰三角形．
解：如图，设DC与BE的交点为F， ∵AB=AC，
∴△ABC是等腰三角形；
∴∠ABC=∠ACB
由AB、AC分别为∠ABC、∠ACB的角平分线得，
∠EBC= ( http: / / www.21cnjy.com / )∠ABC，∠DCB= ( http: / / www.21cnjy.com / )∠ACB
∴∠EBC=∠ACB
∴△BFC是等腰三角形，
由题设中的条件不足以判断其他三角形的形状，
综上，由题设只能得出△ABC、△BFC为等腰三角形，
故选A．
( http: / / www.21cnjy.com / )
【分析】由∠A=∠ACD，得AD=CD，再由∠B=∠BCD得CD=DB，利用等量代换即可解题．
解：∵∠A=∠ACD，∴AD=CD， ∵∠B=∠BCD∴CD=DB，
因AD和DB都等于同一个量CD，
所以AD=DB，依据是等量代换．
故选C．
【分析】利用等腰三角形的概念、性质以及角平分线的性质做题．　
解：∵AB=AC，AD平分∠BAC，DE⊥AB，DF⊥AC
∴△ABC是等腰三角形，AD⊥BC，BD=CD，∠BED=∠DFC=90°
∴DE=DF
∴AD垂直平分EF
∴（4）错误；
又∵AD所在直线是△ABC的对称轴，
∴（1）∠DEF=∠DFE；（2）AE=AF；（3）AD平分∠EDF．
故选C．
【分析】①根据等腰三角形的性质和三角 ( http: / / www.21cnjy.com )形的内角和来分析；②根据等腰三角形的性质和三角形的内角和来分析；③根据三角形内角和和等腰直角三角形的性质来分析；④根据等腰三角形的性质和三角形的内角和来分析；2·1·c·n·j·y
解：①作底角的角平分线即可；被一条直线分成两个小等腰三角形的角的度数分别为：36°，36°，108°；36°，72°，72°.
②不能.
③作底边上的高即可，根据直角三角形中斜边上的中线等于斜边的一半，即直角三角形斜边上的中线把它分成了两个等腰三角形.
④在BC上截取BD=AB即可；被一条直线分成两个小等腰三角形的角的度数分别为：36°，72°，72°；36°，36°，108°.
故答案为：D.
【分析】如图，作CD⊥AB， ( http: / / www.21cnjy.com )则CD是等边△ABC底边AB上的高，根据等腰三角形的三线合一，可得AD=1，所以，在直角△ADC中，利用勾股定理，可求出CD的长，代入面积计算公式，解答出即可；
解：作CD⊥AB，
∵△ABC是等边三角形，AB=BC=AC=2，
∴AD=1，
∴在直角△ADC中，
CD= ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / )，
∴S△ABC= ( http: / / www.21cnjy.com / )×2× ( http: / / www.21cnjy.com / )= ( http: / / www.21cnjy.com / )；
故选C．
( http: / / www.21cnjy.com / )
【分析】根据平行线性质和角平分线定义 ( http: / / www.21cnjy.com )得出∠EDB=∠EBD，推出BE=ED，同理DF=CF，求出△AEF的周长=AB+AC，代入求出即可．　
解：∵EF∥BC，
∴∠EDB=∠DBC，
∵BD平分∠ABC，
∴∠EBD=∠CBD，
∴∠EDB=∠EBD，
∴BE=ED，
同理DF=CF，
∴△AEF的周长是AE+EF+AF
=AE+ED+DF+AF
=AE+BE+CF+AF
=AB+AC
=5+7
=12．
故选B．
【分析】利用三角形的内角和得到∠B+∠C=120°，再利用四边形的内角和求得结论即可．　
解：∵∠CAB=60°，
∴∠B+∠C=120°，
在四边形BCED中，
∠1+∠2=360°﹣∠B﹣∠C=240°．
故选：C
【分析】可作出AB的中垂线m，在直线l上 ( http: / / www.21cnjy.com )的任何一点P可使得PA=PD，PB=PC，所以只要点P还满足PA=PB或PA=AB或PB=AB三种情况即可.
解： 如图，当以AB为底边时，只在P1符合；
当以AB为腰时，以AB为半径，分别以A，B为圆心作圆，与直线l分别交于点P2 ， P3 ， 此时P2 ， P3符合；
( http: / / www.21cnjy.com / )
故选C
【分析】根据题意，结合图形，分两种情况讨论：①OA为等腰三角形底边；②OA为等腰三角形一条腰．
解：如上图：①OA为等腰三角形底边，符合符合条件的动点P有一个；
②OA为等腰三角形一条腰，符合符合条件的动点P有三个．
综上所述，符合条件的点P的个数共4个．
故选C．
( http: / / www.21cnjy.com / )
解：如图所示：当BC1=A ( http: / / www.21cnjy.com )C1，AC=CC2，AB=BC3，AC4=CC4，AB=AC5，AB=AC6，BC7=CC7时，都能得到符合题意的等腰三角形．21·cn·jy·com
故选：B．
( http: / / www.21cnjy.com / )
二 、填空题
【分析】根据已知条件求证△EBO≌△DCO，然后可得∠OBC=∠OCB再利用两角相等即可判定△ABC是等腰三角形．此题答案不唯一．【出处：21教育名师】
答：由①③条件可判定△ABC是等腰三角形．
证明：∵∠EBO=∠DCO，∠EOB=∠DOC，（对顶角相等）
BE=CD，
∴△EBO≌△DCO，
∴OB=OC，
∴∠OBC=∠OCB，
∴∠ABC=∠ACB，
∴△ABC是等腰三角形．
【分析】分AB是腰长时，根据网格结构 ( http: / / www.21cnjy.com )，找出一个小正方形与A．B顶点相对的顶点，连接即可得到等腰三角形，AB是底边时，根据线段垂直平分线上的点到线段两端点的距离相等，AB垂直平分线上的格点都可以作为点C，然后相加即可得解．　
解：如图，AB是腰长时，红色的4个点可以作为点C，
AB是底边时，黑色的4个点都可以作为点C，
所以，满足条件的点C的个数是4+4=8．
故答案为8．
( http: / / www.21cnjy.com / )
【分析】建立平面直角坐标系，在平面直 ( http: / / www.21cnjy.com )角坐标系中，作出点A和点B，点C为x轴上的点，连接AB，AB边可能是底边，也可能是腰，分两种情况，得到点C的坐标．
解：∵AB=AC，D是BC边的中点，∴∠BAD= ( http: / / www.21cnjy.com / )=25°．
故答案为：25°
【分析】根据已知条件求证△EBO≌△DCO，然后可得∠OBC=∠OCB再利用两角相等即可判定△ABC是等腰三角形．此题答案不唯一．www.21-cn-jy.com
答：由①③条件可判定△ABC是等腰三角形．
证明：∵∠EBO=∠DCO，∠EOB=∠DOC，（对顶角相等）
BE=CD，
∴△EBO≌△DCO，
∴OB=OC，
∴∠OBC=∠OCB，
∴∠ABC=∠ACB，
∴△ABC是等腰三角形．
解：∵A（0，3），B（4，0），
∴OA=3．OB=4，
∴AB=5，
①当AB=AC=5，则OC=4，
∴C（﹣4，0），
②当AB=BC=5，点C在x轴上，且在B的左侧，则OC=5﹣4=1，
∴C（﹣1，0），
③当AC=BC，则OC2=AC2﹣OA2 ， 即OC2=（4﹣OC）2﹣32 ，
∴OC= ( http: / / www.21cnjy.com / )，
∴C（ ( http: / / www.21cnjy.com / )， 0），
综上所述：C（﹣4，0），（﹣1，0），（ ( http: / / www.21cnjy.com / )， 0）．
故答案为：（﹣4，0），（﹣1，0），（ ( http: / / www.21cnjy.com / )， 0）．
( http: / / www.21cnjy.com / )
【分析】分三种情况讨论：先确定特殊位置时成立的x值，
①如图1，当M与O重合时，即x=0时，点P恰好有三个；
②如图2，构建腰长为4的等腰直角△OMC，和半径为4的⊙M，发现M在点D的位置时，满足条件；
③如图3，根据等腰三角形三种情况的画法： ( http: / / www.21cnjy.com )分别以M、N为圆心，以MN为半径画弧，与OB的交点就是满足条件的点P，再以MN为底边的等腰三角形，通过画图发现，无论x取何值，以MN为底边的等腰三角形都存在一个，所以只要满足以MN为腰的三角形有两个即可． 21·世纪*教育网
解：分三种情况：
①如图1，当M与O重合时，即x=0时，点P恰好有三个；
( http: / / www.21cnjy.com / )
②如图2，以M为圆心，以4为半径画圆，当⊙M与OB相切时，设切点为C，⊙M与OA交于D，
( http: / / www.21cnjy.com / )
∴MC⊥OB，
∵∠AOB=45°，
∴△MCO是等腰直角三角形，
∴MC=OC=4，
∴OM=4 ( http: / / www.21cnjy.com / )，
当M与D重合时，即x=OM﹣DM=4 ( http: / / www.21cnjy.com / )﹣4时，同理可知：点P恰好有三个；
③如图3，取OM=4，以M为圆心，以OM为半径画圆，
则⊙M与OB除了O外只有一个交点，此时x=4 ( http: / / www.21cnjy.com )，即以∠PMN为顶角，MN为腰，符合条件的点P有一个，以N圆心，以MN为半径画圆，与直线OB相离，说明此时以∠PNM为顶角，以MN为腰，符合条件的点P不存在，还有一个是以NM为底边的符合条件的点P； 点M沿OA运动，到M1时，发现⊙M1与直线OB有一个交点；www-2-1-cnjy-com
∴当4＜x＜4 ( http: / / www.21cnjy.com / )时，圆M在移动过程中，则会与OB除了O外有两个交点，满足点P恰好有三个；
综上所述，若使点P，M，N构成等腰三角形的点P恰好有三个，则x的值是：x=0或x=4 ( http: / / www.21cnjy.com / )﹣4或4 ( http: / / www.21cnjy.com / )．
故答案为：x=0或x=4 ( http: / / www.21cnjy.com / )﹣4或4 ( http: / / www.21cnjy.com / )．
( http: / / www.21cnjy.com / )
三 、解答题
证明：∵OC=OD
∴∠D=∠C
∵AB//DC
∴∠B =∠D，∠A =∠C
∴∠A =∠B
∴OA=OB
【分析】由矩形ABCD，可得AD∥ ( http: / / www.21cnjy.com )BC，得到∠1=∠2，由BD为折痕，得到∠2=∠3，通过等量代换得到∠1=∠3，根据等腰三角形的判定得到此三角形为等腰三角形．
解:△BDF是等腰三角形
∵△ABD翻折后得△A/BD
∴△ABD≌△A/BD
∴∠1＝∠2
∵四边形ABCD是矩形
∴AD∥BC
∴∠1＝∠3
∴∠2＝∠3
∴BF＝DF（等角对等边）
∴△BDF是等腰三角形
【分析】利用HL定理得出△ABD≌△BAC即可得出∠DBA=∠CAB，再利用等腰三角形的判定得出即可．21教育网
证明：∵AC⊥BC，BD⊥AD
∴∠D=∠C=90°，
在Rt△ABD和Rt△BAC中，
( http: / / www.21cnjy.com / )，
∴Rt△ABD≌Rt△BAC（HL），
∴∠DBA=∠CAB，
∴OA=OB，
即△OAB是等腰三角形．
另外一种证法：
证明：∵AC⊥BC，BD⊥AD
∴∠D=∠C=90°
在Rt△ABD和Rt△BAC中
( http: / / www.21cnjy.com / )
∴Rt△ABD≌Rt△BAC（HL）
∴AD=BC，
在△AOD和△BOC中
( http: / / www.21cnjy.com / )，
∴△AOD≌△BOC（AAS），
∴OA=OB，
即△OAB是等腰三角形．
( http: / / www.21cnjy.com / )
【分析】（1）由勾股定理即可求出AB，
（2）根据平行线性质推出∠D=∠DCB ( http: / / www.21cnjy.com )，∠E=∠EBC，推出∠D=∠ACD，∠E=∠ABE，求出AD=AC=6，AE=AB=8，即可求出答案．2-1-c-n-j-y
解：（1）∵在Rt△ABC中，∠BAC=90°，AC=6，BC=10，
∴AB=8，
（2）∵BE平分∠ABC，
∴∠ABE=∠EBC，
又∵DE∥BC，
∴∠AEB=∠EBC，
∴∠ABE=∠AEB，
∴AE=AB=8，
同理，∵DC平分∠ACB，DE∥BC，
∴AD=AC=6
∴DE=14
证明：如图，过D作DG∥AC交BC于G，
( http: / / www.21cnjy.com / )
则∠GDF=∠E，
∠DGB=∠ACB，
在△DFG和△EFC中，
( http: / / www.21cnjy.com / )
∴△DFG≌△EFC(ASA)．
∴CE=GD，∵BD=CE.∴BD=GD.
∴∠B=∠DGB.∴∠B=∠ACB.
∴△ABC为等腰三角形．
解：（1）当AB的中垂线MN交AC边时，如图，
∵　∠DEA＝50°，
∴　∠A＝90°－50°＝40°，
∵　AB＝AC，
∴　∠B＝ ( http: / / www.21cnjy.com / )（180°－40°）＝70°；
（2）当AB的中垂线MN交CA的延长线时，如下图，
( http: / / www.21cnjy.com / )
∵　∠DEA＝50°，
∴　∠BAC＝90°＋50°＝140°，
∴　∠B＝ ( http: / / www.21cnjy.com / )（180°－140°）＝20°．
【分析】（1）由等边三角形的性质得出∠ ( http: / / www.21cnjy.com )ABC=∠ACB=60°，∠BCE=30°，再证出∠BED=∠D，得出BE=DB，即可得出AE=DB；【来源：21cnj*y.co*m】
（2）由等边三角形的性质得出∠AB ( http: / / www.21cnjy.com )C=∠ACB=∠A=60°，∠DBE=120°，再证出△AEF是等边三角形，得出AE=EF，BE=CF，证出∠FEC=∠D，证明△EFC≌△DBE，得出EF=DB，即可得出AE=DB．
解：（1）AE=DB；理由如下：
∵△ABC是等边三角形，点E为AB的中点，
∴∠ABC=∠ACB=60°，∠BCE= ( http: / / www.21cnjy.com / )∠ACB=30°，AE=BE，
∵ED=EC，
∴∠D=∠BCE=30°，
∵∠ABC=∠D+∠BED，
∴∠BED=30°=∠D，
∴BE=DB，
∴AE=DB；
故答案为：=；
（2）AE=DB，理由如下：
过点E作EF∥BC，交AC于点F，如图2所示：
∵△ABC是等边三角形，
∴∠ABC=∠ACB=∠A=60°，
∴∠DBE=120°，
∵EF∥BC，
∴∠AEF=∠ABC，∠AFE=∠ACB，∠FEC=∠DCE，
∴∠A=∠AEF=∠AFE=60°，
∴△AEF是等边三角形，∠EFC=120°，
∴AE=EF，
∴BE=CF，
∵ED=EC，
∴∠D=∠DCE，
∴∠FEC=∠D，
在△EFC和△DBE中，，
∴△EFC≌△DBE（AAS），
∴EF=DB，
∴AE=DB；
故答案为：=．
( http: / / www.21cnjy.com / )
【分析】（1）由PO=PD，利用等 ( http: / / www.21cnjy.com )边对等角和三角形内角和定理可求得∠POD=67.5°，∠OPB=67.5°，然后利用等角对等边可得出结论；
（2）过点O作OC⊥AB于C，首先利用 ( http: / / www.21cnjy.com )等腰直角三角形的性质可以得到∠COB=∠B=45°，OC=5，然后证得∠POC=∠DPE，进而利用AAS证明△POC≌△DPE，再根据全等三角形的性质可得OC=PE．
（1）证明：∵PO=PD，∠OPD=45°，
∴∠POD=∠PDO= ( http: / / www.21cnjy.com / )=67.5°，
∵等腰直角三角形AOB中，AO⊥OB，
∴∠B=45°，
∴∠OPB=180°﹣∠POB﹣∠B=67.5°，
∴∠POD=∠OPB，
∴BP=BO，即△BOP是等腰三角形；
（2）解：PE的值不变，为PE=5，证明如下：
如图，过点O作OC⊥AB于C，
∵∠AOB=90°，AO=BO，
∴△BOC是等腰直角三角形，∠COB=∠B=45°，点C为AB的中点，
∴OC= ( http: / / www.21cnjy.com / )AB=5，
∵PO=PD，
∴∠POD=∠PDO，
又∵∠POD=∠COD+∠POC=45°+∠POC，∠PDO=∠B+∠DPE=45°+∠DPE，
∴∠POC=∠DPE，
在△POC和△DPE中，
( http: / / www.21cnjy.com / )，
∴△POC≌△DPE（AAS），
∴OC=PE=5，
∴PE的值不变，为5．
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
版权所有@21世纪教育网(www.21cnjy.com)